算法思想总结:位运算
创作不易,感谢三连支持!!
一、常见的位运算总结




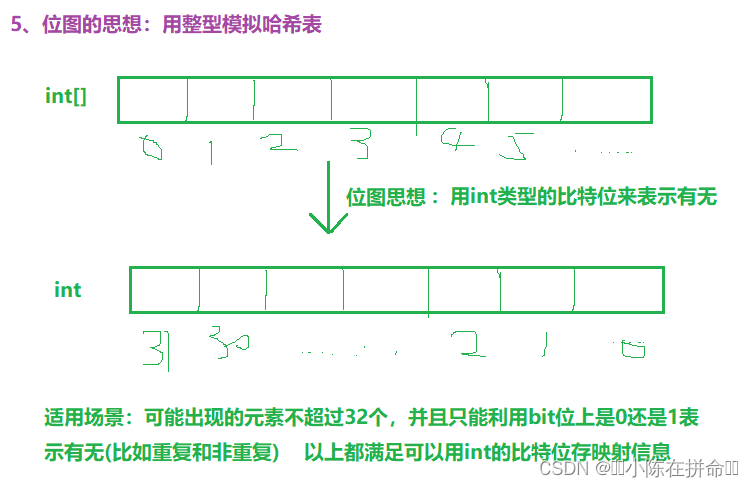





二、位1的个数
. - 力扣(LeetCode)

利用第七条特性:n&(n-1)干掉最后一个1,然后每次都用count++去统计,直到变成0
class Solution {
public:int hammingWeight(uint32_t n) {int count=0;while(n){n&=(n-1);++count;} return count;}
};三、汉明距离
. - 力扣(LeetCode)

利用异或相同为0相异为1的特点,x和y异或后不一样的位都会变成1,这个时候再用n&(n-1)去统计1个个数,即为这两个数字的汉明距离
class Solution {
public:int hammingDistance(int x, int y) {//异或的特点,相同为0,相异为1 然后再利用n&(n-1)统计1的个数int n=x^y;int count=0;while(n){n&=(n-1);++count;}return count;}
};四、比特数记位(典型dp)

思路1:每遍历一个数都用n&(n-1)去数他一共有多少个1,然后放心ans数组中
class Solution {
public:int countOnes(int x){int ones=0;while(x){x&=(x-1);++ones;}return ones;}//利用vector<int> countBits(int n) {vector<int> ret(n+1);for(int i=1;i<=n;++i) ret[i]=countOnes(i);return ret;}
};思路2:动态规划思想(本质是根据位运算的性质通过已经计算出来的状态去求未计算的状态)
即当计算 i 的「一比特数」时,如果存在 0≤j<i,j 的「一比特数」已知,且 i和 j 相比,i 的二进制表示只比j多了一个 1,则可以快速得到 i 的「一比特数」。(利用位运算的性质)
1、设置最低位
对于n(n-1),本质上是将最右侧的1干掉,所以一定会比原来的n小!!
因此bit[i]=bit[i&(i-1)]+1 恒成立!!
class Solution {
public:vector<int> countBits(int n) {vector<int> ret(n+1);for(int i=1;i<=n;++i) ret[i]=ret[i&(i-1)]+1;return ret;}
};2、最低有效位
对于正整数x来说,如果是偶数的话,右移一位正好就是x/2,并且1的个数不会变,所以偶数bit[i]=bit[i/2] 对于奇数来说,右移一位会丢掉后面的1,所以要给他补上去,所以奇数等于bit[i]=bit[i/2]+1 为了修正奇数多出来的1,我们可以利用i&1,如果是奇数就是1,偶数就是0,因此 bit[i]=bit[i/2]+(i&1) 恒成立!!
class Solution {
public:vector<int> countBits(int n) {vector<int> ret(n+1);for(int i=1;i<=n;++i) ret[i]=ret[i/2]+(i&1);return ret;}
};3、最高有效位
对于正整数 x,如果可以知道最大的正整数 y,使得 y≤x,y 是 2的整数次幂,则 y的二进制表示中只有最高位是 1,其余都是 0,此时称 y 为 x 的「最高有效位」。令 z=x−y,显然 0≤z<x,则 bits[x]=bits[z]+1,所以我们使用heightbit作为当前的最高有效位。如果i&(i-1)为最高有效位,就更新heightbit,i 比 i−highBit的「一比特数」多 1 所以bit[i]=bit[i-height]+1 恒成立!!
class Solution {
public:vector<int> countBits(int n) {vector<int> ret(n+1);int heightbit=0;for(int i=1;i<=n;++i) {if((i&(i-1))==0) heightbit=i;ret[i]=ret[i-heightbit]+1;}return ret;}
};五、只出现一次的数字(1)
. - 力扣(LeetCode)

思路:利用异或的性质,出现两次的数异或后为0,出现一次的数异或0还是本身
class Solution {
public:int singleNumber(vector<int>& nums) {int n=0;for(auto &e:nums) n^=e;return n;}
};六、只出现一次的数字(2)
. - 力扣(LeetCode)


class Solution {
public:int singleNumber(vector<int>& nums) {int ret=0;for(int i=0;i<32;++i){int sum=0;for(int num:nums) if((num>>i)&1) ++sum;//统计个数每一个1的比特位sum%=3;//模3后代表ret当前bit位的值if(sum==1) ret|=(1<<i);//sum==1就让ret该位置变成1}return ret;}
};七、只出现一次的数字(3)

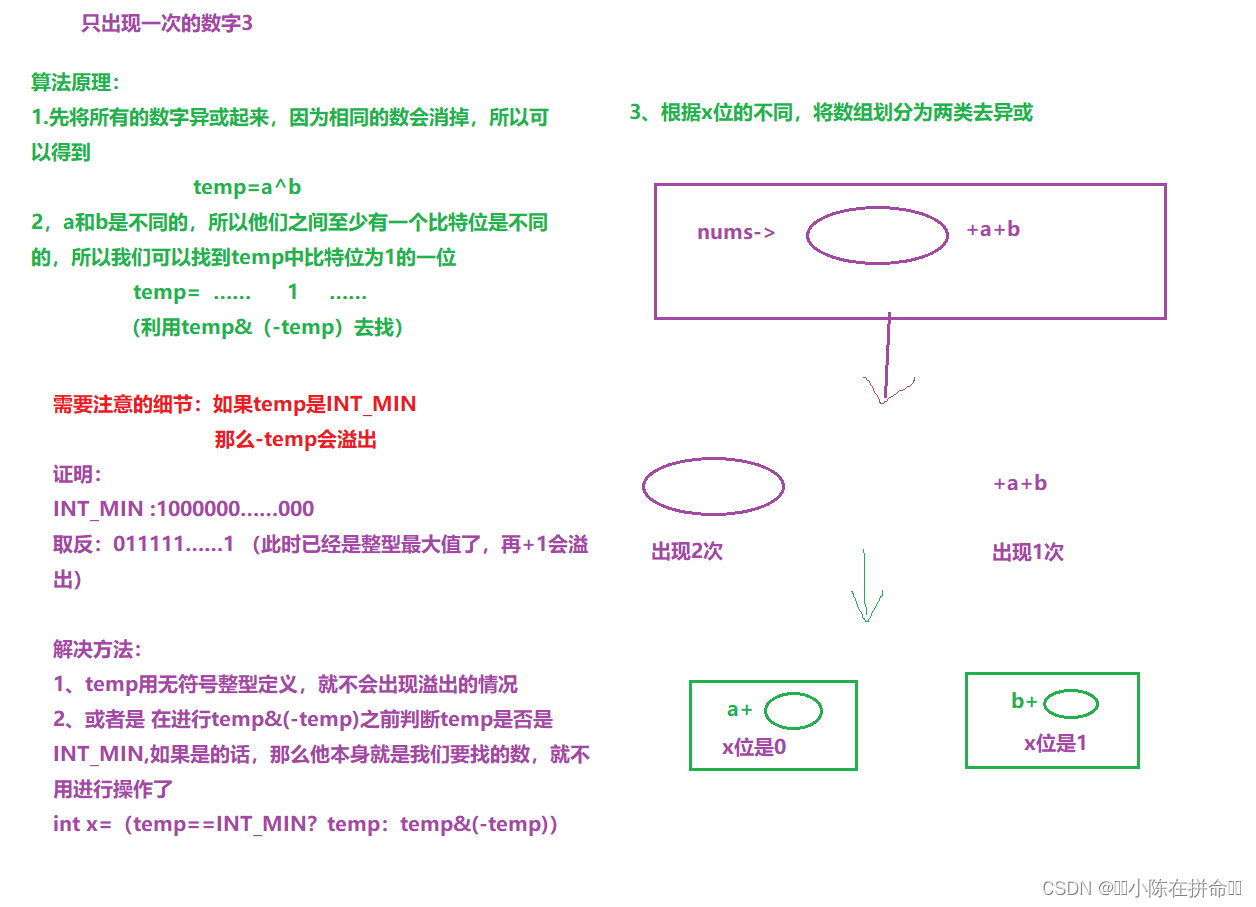
class Solution {
public:vector<int> singleNumber(vector<int>& nums) {unsigned int temp=0;//遇到INT_MIN会溢出,10000……00for(int num:nums) temp^=num;int x=temp&(-temp);//x拿到最后一个1//int x= (temp == temp ? temp : temp & (-temp));int type1=0,type2=0;for(int num:nums) if(num&x) type1^=num; else type2^=num;return {type1,type2};}
};八、丢失的数字
. - 力扣(LeetCode)

思路1:利用等差数列和的公式-数组每一位数相加,即可得到消失的数
class Solution {
public:int missingNumber(vector<int>& nums) {int n=nums.size();return n*(n+1)/2-accumulate(nums.begin(),nums.end(),0);}
};思路2:利用异或的特点,让0和数组所有数进行异或,再对1-n异或,出现两次的数都会被消去,最后只会留下答案
class Solution {
public:int missingNumber(vector<int>& nums) {int ret=0;for(int num:nums) ret^=num;for(int i=0;i<=nums.size();++i) ret^=i;return ret;}
};思路3:暴力快排+寻找下标和数字对应不上的数
class Solution {
public:int missingNumber(vector<int>& nums) {sort(nums.begin(),nums.end());int n=nums.size();for(int i=0;i<n;++i) if(nums[i]!=i) return i;return n;}
};九、消失的两个数字
. - 力扣(LeetCode)
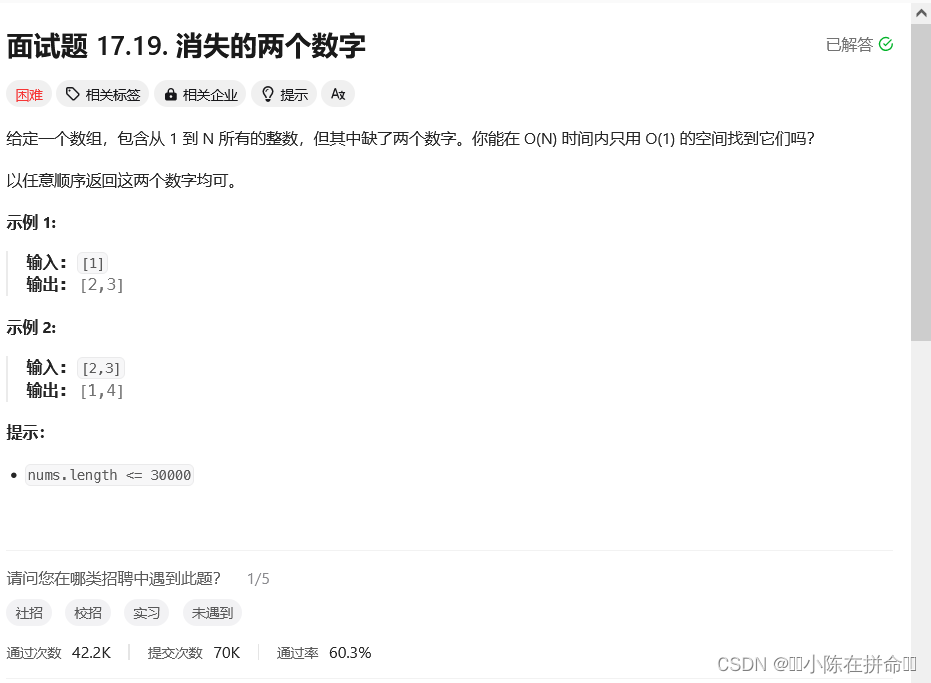
该题就是只出现一次数组(1)和 (3)的结合,所以以上的思路去解答即可
class Solution {
public:vector<int> missingTwo(vector<int>& nums) {int temp=0;for(auto e:nums) temp^=e;for(int i=1;i<=nums.size()+2;++i) temp^=i;int x=temp&(-temp);//拿到最右边的1int num1=0,num2=0;for(auto e:nums) if(e&x) num1^=e; else num2^=e;for(int i=1;i<=nums.size()+2;++i) if(i&x) num1^=i; else num2^=i;return {num1,num2};}
};十、判定字符是否唯一
. - 力扣(LeetCode)

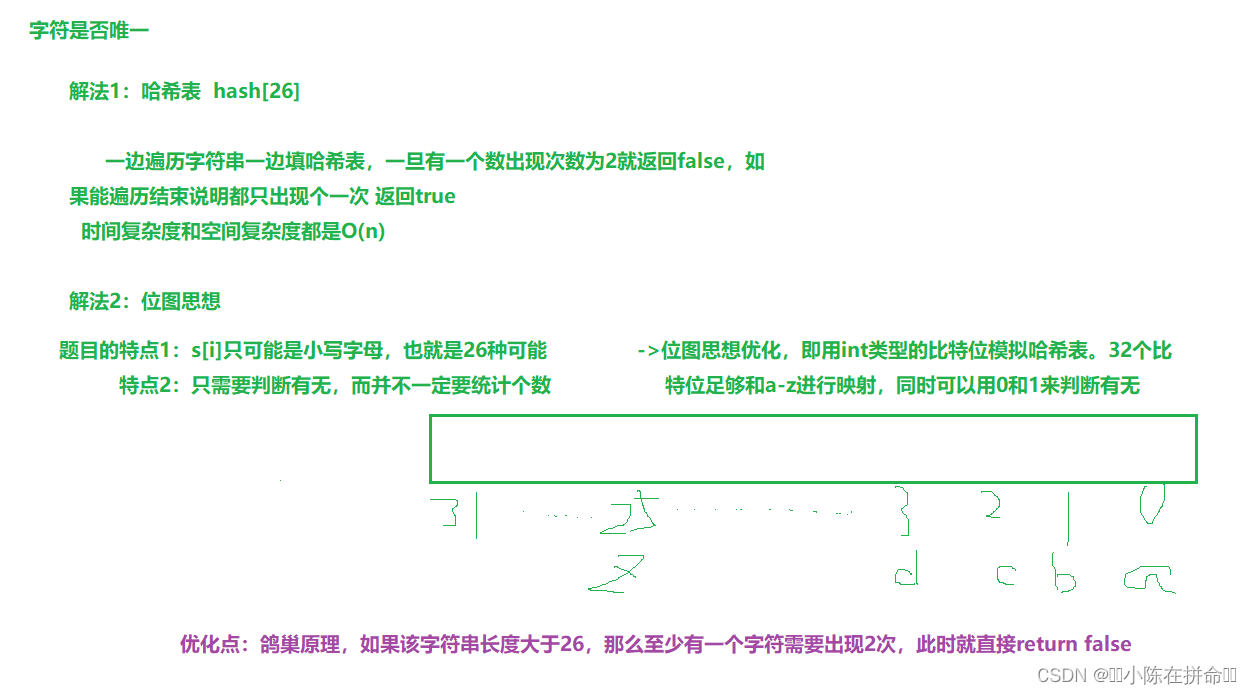
class Solution {
public:bool isUnique(string astr) {if(astr.size()>26) return false;//鸽巢原理做优化//利用位图的思想int bitmap=0;for(auto ch:astr){int i=ch-'a';//找到映射关系if((bitmap>>i)&1==1) return false;//先判断该字符是否出现过 判断第i位是否是1//如果没出现过,将第i位的0修改为1bitmap|=(1<<i);}return true;}
};十一、或运算的最小翻转次数
. - 力扣(LeetCode)

class Solution {
public:int minFlips(int a, int b, int c) {int ret=0;//记录翻转次数for(int i=0;i<31;++i){//找到每一位进行判断int bit_a=(a>>i)&1;int bit_b=(b>>i)&1;int bit_c=(c>>i)&1;//情况1,如果c为0的话,那么a和b必须全是0 所以他们是多少就要翻转几次if(bit_c==0) ret+=(bit_a+bit_b);//情况2,如果c为1的话,那么a和b至少要有一个为1 如果都为0,翻转一次,如果有1就不用翻转else ret+=(bit_a+bit_b==0);}return ret;}
};十二、两整数之和
. - 力扣(LeetCode)


class Solution {
public:int getSum(int a, int b) {//要考虑-1,因为-1的右移操作是没有定义的while(b){int x=a^b;int carry=(a&b)<<1;a=x;b=carry;}return a;}
};
相关文章:

算法思想总结:位运算
创作不易,感谢三连支持!! 一、常见的位运算总结 标题 二、位1的个数 . - 力扣(LeetCode) 利用第七条特性:n&(n-1)干掉最后一个1,然后每次都用count去统计ÿ…...
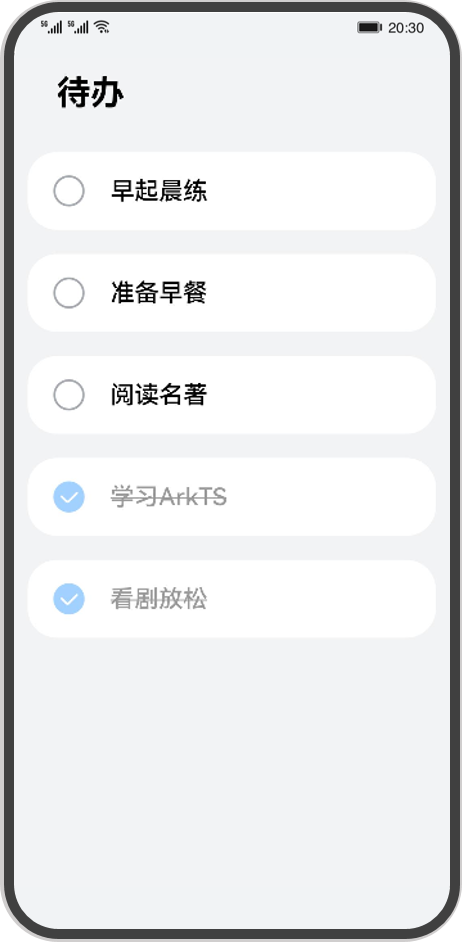
四、HarmonyOS应用开发-ArkTS开发语言介绍
目录 1、TypeScript快速入门 1.1、编程语言介绍 1.2、基础类型 1.3、条件语句 1.4、函数 1.5、类 1.6、模块 1.7、迭代器 2、ArkTs 基础(浅析ArkTS的起源和演进) 2.1、引言 2.2、JS 2.3、TS 2.4、ArkTS 2.5、下一步演进 3、ArkTs 开发实践…...
3 Spring之DI详解
5,DI相关内容 前面我们已经完成了bean相关操作的讲解,接下来就进入第二个大的模块DI依赖注入,首先来介绍下Spring中有哪些注入方式? 我们先来思考 向一个类中传递数据的方式有几种? 普通方法(set方法)构造方法 依赖注入描述了在容器中建…...
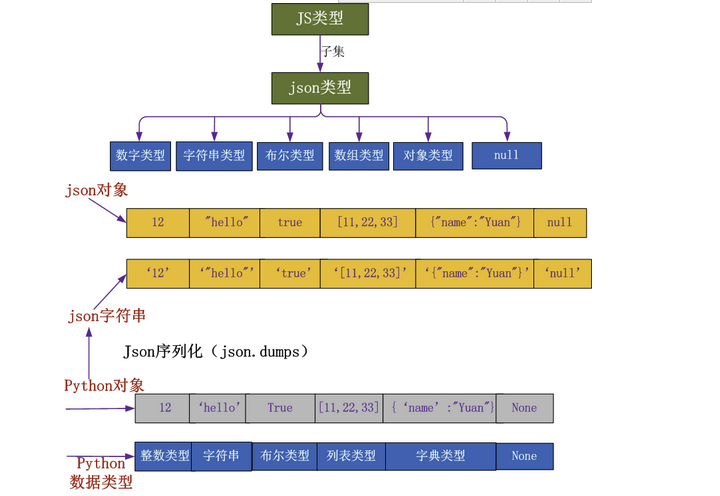
Web框架开发-Ajax
一、 Ajax准备知识:json 1、json(Javascript Obiect Notation,JS对象标记)是一种轻量级的数据交换格式 1 2 它基于 ECMAScript (w3c制定的js规范)的一个子集,采用完全独立于编程语言的文本格式来存储和表示数据。 简洁和清晰的层次结构使得 JSON 成为理想的数据交换语言。…...

Python爬虫之urllib库
1、urllib库的介绍 可以实现HTTP请求,我们要做的就是指定请求的URL、请求头、请求体等信息 urllib库包含如下四个模块 request:基本的HTTP请求模块,可以模拟请求的发送。error:异常处理模块。parse:工具模块&#x…...

Docker学习笔记 - 常用命令
目录 基本概念常用命令使用docker compose启动脚本创建自己的image Docker命令文档 1. 下载一个image 从hub.docker.com下载一个image。 docker pull [image name]下载时指定image的tag。 docker pull [image name]:<tag>举例,下载postgre的tag为alpine…...
)
数学建模(Topsis python代码 案例)
目录 介绍: 模板: 案例: 极小型指标转化为极大型(正向化): 中间型指标转为极大型(正向化): 区间型指标转为极大型(正向化): 标准化处理: 公式: Topsis(优劣解距离法): 公式: 完整代码: 结果: 介绍: 在数学建模中,Topsis方法是一种多准则决策分…...

gateway网关指定路由响应超时时间
gateway网关指定路由响应超时时间 spring:cloud:gateway:httpclient:responseTimeout: 10000这个配置用于设置HttpClient的响应超时时间,单位是毫秒。具体来说,这个配置表示当Gateway向后端服务发出请求后,如果在10秒内没有收到后端服务的响…...
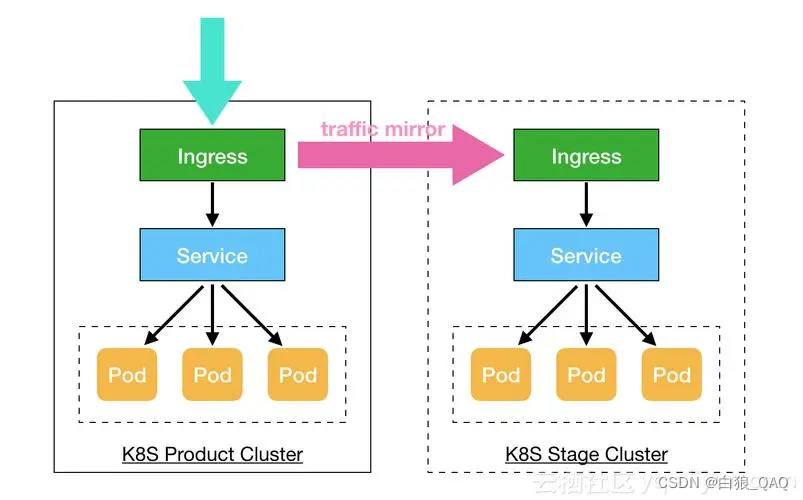
docker 和K8S知识分享
docker知识: 比如写了个项目,并且在本地调试没有任务问题,这时候你想在另外一台电脑或者服务器运行,那么你需要在另外一台电脑或者服务器配置相同的软件,比如数据库,web服务器,必要的插件和库等…...

MySQL--select count(*)、count(1)、count(列名) 的区别你知道吗?
MySQL select count(*)、count(1)、count(列名) 的区别? 这里我们先给出正确结论: count(*),包含了所有的列,会计算所有的行数,在统计结果时候,不会忽略列值为空的情况。count(1),忽略所有的列…...

使用verilog设计实现16位CPU及仿真
这是一个简单的16位CPU(中央处理单元)的设计实验。这个CPU包括指令存储器、数据存储器、ALU(算术逻辑单元)、寄存器文件和控制单元。 设计一个简单的16位CPU的实验通常可以分为以下几个步骤: 指令集设计:首先确定CPU支持的指令集架构,包括指令格式、寄存器组织、地址模…...
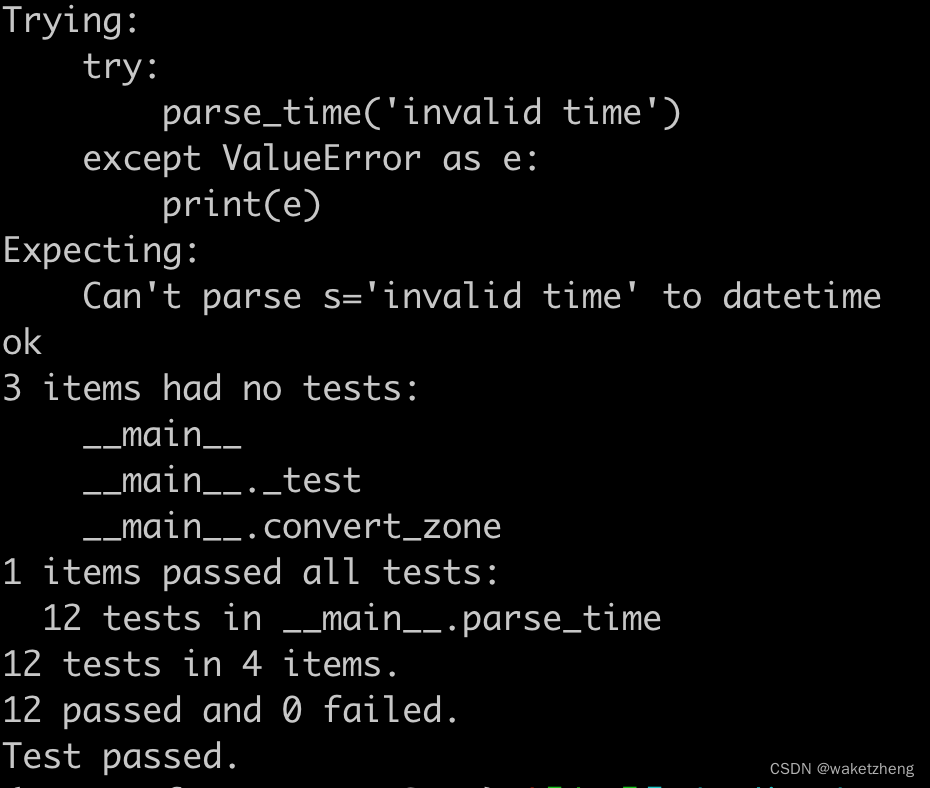
Python将字符串转换为datetime
有这样一些字符串: 1710903685 20240320110125 2024-03-20 11:01:25 要转换成Python的datetime 代码如下: import functools import re from datetime import datetime, timedelta from typing import Union# pip install python-dateutil from date…...

Vue 3 + TypeScript + Vite的现代前端项目框架
随着前端开发技术的飞速发展,Vue 3、TypeScript 和 Vite 构成了现代前端开发的强大组合。这篇博客将指导你如何从零开始搭建一个使用Vue 3、TypeScript以及Vite的前端项目,帮助你快速启动一个性能卓越且类型安全的现代化Web应用。 Vue 3 是一款渐进式Jav…...

浏览器强缓存和弱缓存的主要区别
浏览器强缓存与弱缓存 浏览器的缓存机制主要分为两种:强缓存与协商缓存(也称弱缓存)。 强缓存 强缓存是指浏览器在请求一个资源时,不与服务器发生通信,直接从本地缓存中获取资源。如果存在有效的强缓存,…...

深度学习-2.9梯度不稳定和Glorot条件
梯度不稳定和Glorot条件 一、梯度消失和梯度爆炸 对于神经网络这个复杂系统来说,在模型训练过程中,一个最基础、同时也最常见的问题,就是梯度消失和梯度爆炸。 我们知道,神经网络在进行反向传播的过程中,各参数层的梯…...

地宫取宝dfs
分析: 矩阵里的每一个位置都有标记,要求的问题是:有几种方法能完成这个规定。 那么,我们只需要计算从开始(1,1)到最后(n,m)的深度优先搜索中,有几个是满足要求的即为正确答案。 有个要求是,如果一个格子中…...

Ollama 运行 Cohere 的 command-r 模型
Ollama 运行 Cohere 的 command-r 模型 0. 引言1. 安装 MSYS22. 安装 Golang3. Build Ollama4. 运行 command-r 0. 引言 Command-R Command-R 是一种大型语言模型,针对对话交互和长上下文任务进行了优化。它针对的是“可扩展”类别的模型,这些模型在高…...

2024年C语言最新经典面试题汇总(11-20)
C语言文章更新目录 C语言学习资源汇总,史上最全面总结,没有之一 C/C学习资源(百度云盘链接) 计算机二级资料(过级专用) C语言学习路线(从入门到实战) 编写C语言程序的7个步骤和编程…...

arm linux应用程序crash分析一般方法
目录: 前言一、定位问题的基本方法论1.1 生产环境下系统崩溃的日志信息示例 二、 分析这类什么都没有的app crash的一般方法论:附录:附录1 pmap -p 进程PID 查看进程的内存分配情况附录2 cat /proc/pid/maps 总结 前言 linux的应用程序app开…...

Web安全防护技术解决方案
1、防止爆破 限制请求ip访问次数,超过设定访问次数后,拒绝访问或锁定N分钟后可再次请求 2、调用短信验证码时 加入验证码采用防爆破策略 3、上传后的文件防止被猜出爬取 保存在物理磁盘可进行加密防护文件不能存储在站点目录,防止通过ur…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

阿里云Ubuntu 22.04 64位搭建Flask流程(亲测)
cd /home 进入home盘 安装虚拟环境: 1、安装virtualenv pip install virtualenv 2.创建新的虚拟环境: virtualenv myenv 3、激活虚拟环境(激活环境可以在当前环境下安装包) source myenv/bin/activate 此时,终端…...

内窥镜检查中基于提示的息肉分割|文献速递-深度学习医疗AI最新文献
Title 题目 Prompt-based polyp segmentation during endoscopy 内窥镜检查中基于提示的息肉分割 01 文献速递介绍 以下是对这段英文内容的中文翻译: ### 胃肠道癌症的发病率呈上升趋势,且有年轻化倾向(Bray等人,2018&#x…...

Redis上篇--知识点总结
Redis上篇–解析 本文大部分知识整理自网上,在正文结束后都会附上参考地址。如果想要深入或者详细学习可以通过文末链接跳转学习。 1. 基本介绍 Redis 是一个开源的、高性能的 内存键值数据库,Redis 的键值对中的 key 就是字符串对象,而 val…...


