手撕算法-买卖股票的最佳时机 II(买卖多次)
描述

分析
使用动态规划。
dp[i][0] 代表 第i天没有股票的最大利润
dp[i][1] 代表 第i天持有股票的最大利润
状态转移方程为:
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i]); // 前一天没有股票,和前一天有股票今天卖掉的最大值
dp[i][1] = max(dp[i-1][0] - prices[i], dp[i-1][1]); // 前一天没有股票今天买,和前一天也有股票的最大值
初始状态:
dp[0][0] = 0; // 第一天不持有股票
dp[0][1] = prices[0]; // 第一天持有股票,需要减去第一天的股票价格
返回值:
dp[n - 1][0];// 最后一天必须卖掉股票
代码
根据初始状态和状态转移方程写出代码
class Solution {public int maxProfit(int[] prices) {int n = prices.length;int[][] dp = new int[n][2];dp[0][0] = 0;dp[0][1] = -prices[0];for (int i = 1; i < n; i++) {dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]); // 前一天没有股票,和前一天有股票今天卖掉的最大值dp[i][1] = Math.max(dp[i - 1][0] - prices[i], dp[i - 1][1]); // 前一天没有股票今天买,和前一天也有股票的最大值}return dp[n - 1][0];// 最后一天必须卖掉股票}
}
面试公司
相关文章:

手撕算法-买卖股票的最佳时机 II(买卖多次)
描述 分析 使用动态规划。dp[i][0] 代表 第i天没有股票的最大利润dp[i][1] 代表 第i天持有股票的最大利润 状态转移方程为:dp[i][0] max(dp[i-1][0], dp[i-1][1] prices[i]); // 前一天没有股票,和前一天有股票今天卖掉的最大值dp[i][1] max(dp[i-1…...

技术创新与产业升级
在政府工作报告中,新兴技术如云计算、大数据、人工智能等被多次提及,这反映了政府高度重视新一代信息技术在推动经济社会发展中的重要作用。对于计算机行业而言,抓住这些新兴技术的发展机遇,推动技术创新和产业升级,将是未来发展的关键所在。 云计算作为一种新兴的计算模式,正…...
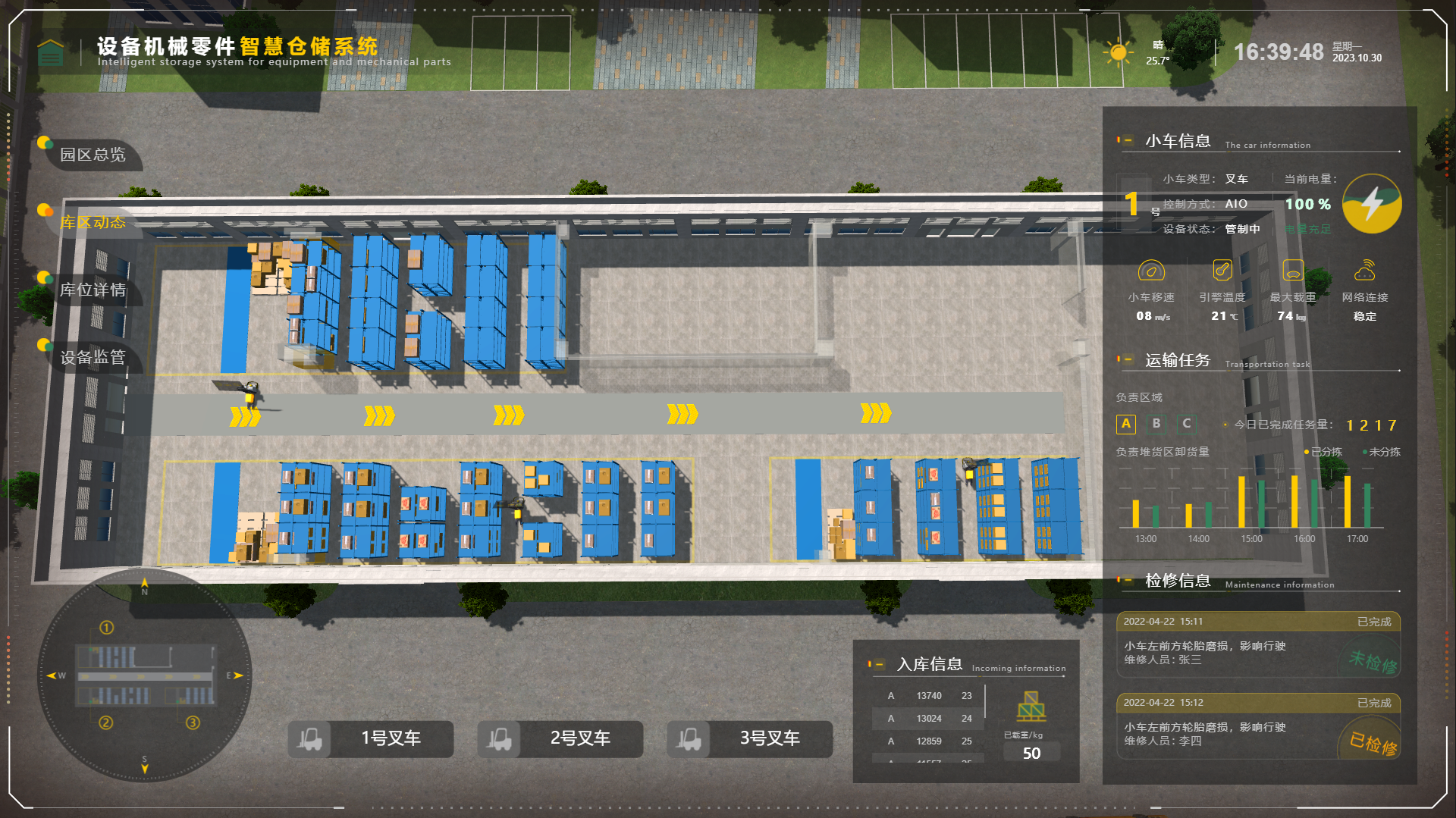
透视未来工厂:山海鲸可视化打造数字孪生新篇章
在信息化浪潮的推动下,数字孪生工厂项目正成为工业制造领域的新宠。作为一名山海鲸可视化的资深用户,我深感其强大的数据可视化能力和数字孪生技术在工厂管理中的应用价值,同时我们公司之前也和山海鲸可视化合作制作了一个智慧工厂项目&#…...

三.寄存器(内存访问)
1.内存中字的存储 2.并不是所有cpu都支持将数据段送入段寄存器,所以有时候用个别的寄存器先把数据段存储起来,再把该寄存器mov到段寄存器。 3.字的传送 4.栈 5.栈机制 举例说明 6.栈顶超界问题 push超界 pop超界 7.栈段...

Day31 贪心算法
Day31 贪心算法 455.分发饼干 我的思路: 小孩数组g指针一直前移,只有饼干数组s满足条件时,才前移,并且更新num 解答: class Solution {public int findContentChildren(int[] g, int[] s) {Arrays.sort(g);Arrays.…...
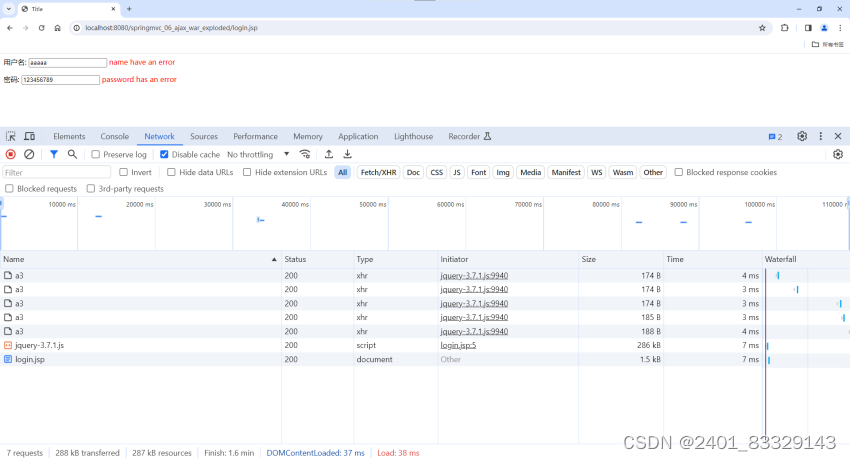
【WEEK4】 【DAY5】AJAX - Part Two【English Version】
2024.3.22 Friday Following the previous article 【WEEK4】 【DAY4】AJAX - Part One【English Version】 Contents 8.4. Ajax Asynchronous Data Loading8.4.1. Create User.java8.4.2. Add lombok and jackson support in pom.xml8.4.3. Change Tomcat Settings8.4.4. Mo…...
力扣100热题[哈希]:最长连续序列
原题:128. 最长连续序列 题解: 官方题解:. - 力扣(LeetCode)题解,最长连续序列 :哈希表 官方解题思路是先去重,然后判断模板长度的数值是否存在,存在就刷新,…...
)
python笔记基础--文件和存储数据(7)
目录 1.从文件中读取数据 2.写入文件 3.存储数据 3.1使用json.dump()和json.load() 3.2保存和读取用户生成的数据 3.3重构 1.从文件中读取数据 读取整个文件 with open(data.txt) as file_object: contents file_object.read()print(contents)print(contents.rstrip…...
)
Vue黑马笔记(最新)
VUE vue是一个用于构建用户界面的渐进式框架 创建一个VUE实例 核心步骤: 准备容器引包(官网)-开发版本/生产版本创建一个vue实例 new vue()指定配置项->渲染数据 el指定挂载点(选择器),指定管理的是哪个容器。dat…...

安全工具介绍 SCNR/Arachni
关于SCNR 原来叫Arachni 是开源的,现在是SCNR,商用工具了 可试用一个月 Arachni Web Application Security Scanner Framework 看名字就知道了,针对web app 的安全工具,DASTIAST吧 安装 安装之前先 sudo apt-get update sudo…...

赋能数据收集:从机票网站提取特价优惠的JavaScript技巧
背景介绍 在这个信息时代,数据的收集和分析对于旅游行业至关重要。在竞争激烈的市场中,实时获取最新的机票特价信息能够为旅行者和旅游企业带来巨大的优势。 随着机票价格的频繁波动,以及航空公司和旅行网站不断推出的限时特价优惠ÿ…...
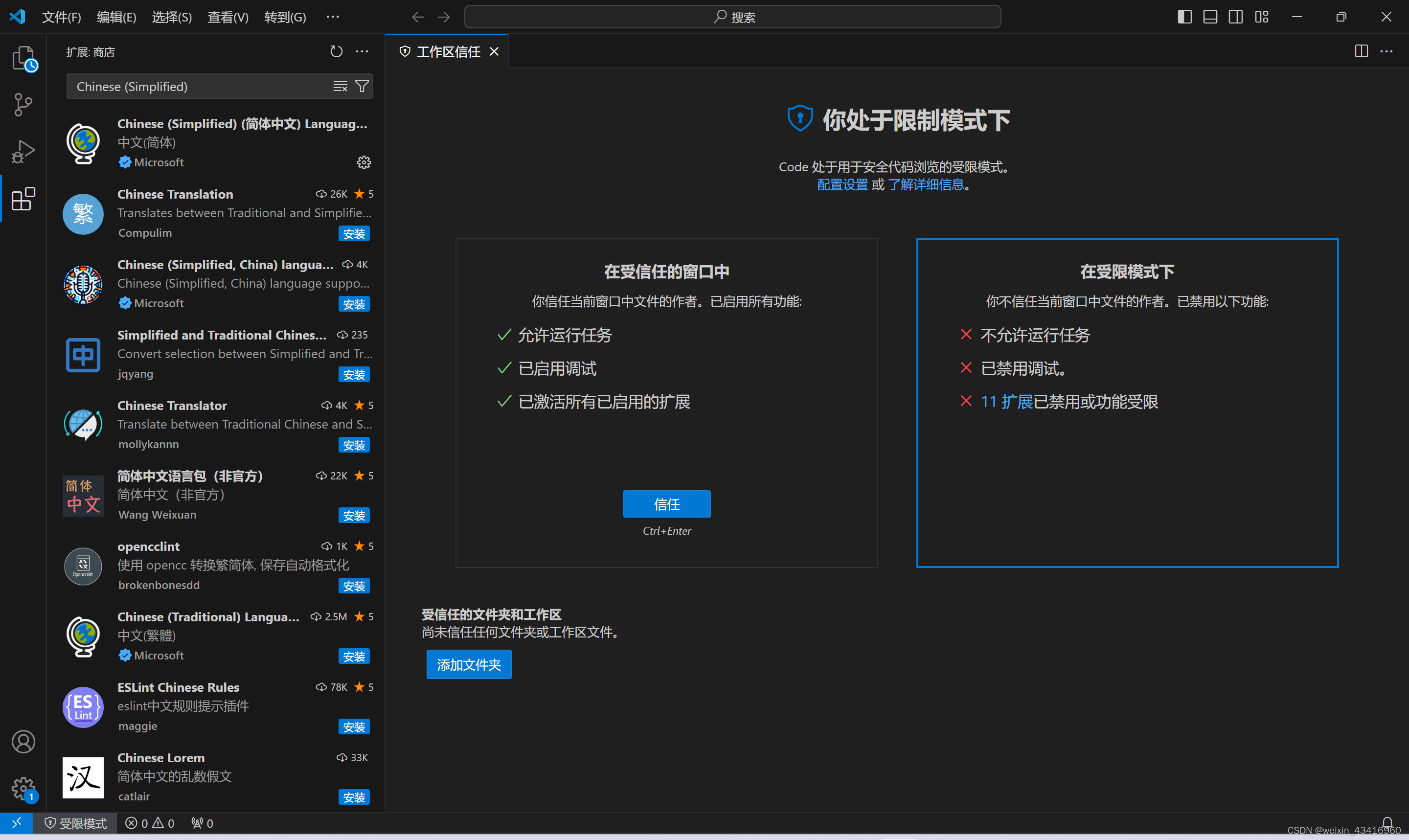
【大模型】在VS Code(Visual Studio Code)上安装中文汉化版插件
文章目录 一、下载安装二、配置显示语言(一)调出即将输入命令的搜索模式(二)在大于号后面输入:Configure Display Language(三)重启 三、总结 【运行系统】win 11 【本文解决的问题】 1、英文不…...

自定义WordPress顶部的菜单的方法
要自定义WordPress顶部的菜单,你需要使用WordPress的菜单系统。首先,你需要创建自定义菜单,然后将其设置为顶部导航菜单。 以下是创建自定义菜单并设置其为顶部导航菜单的步骤: 登录到WordPress管理界面。转到“外观”>“菜单…...

独孤思维:流量暴涨,却惨遭违规
最近独孤操作虚拟资料短视频,有个很深的感悟。 每天发10条短视频,积累到20天左右,播放量和粉丝数开始暴涨。 虽然很多牛比的比我数据好,但是对于刚做短视频的独孤来说,我已经满足了。 但是又发了10来天,…...
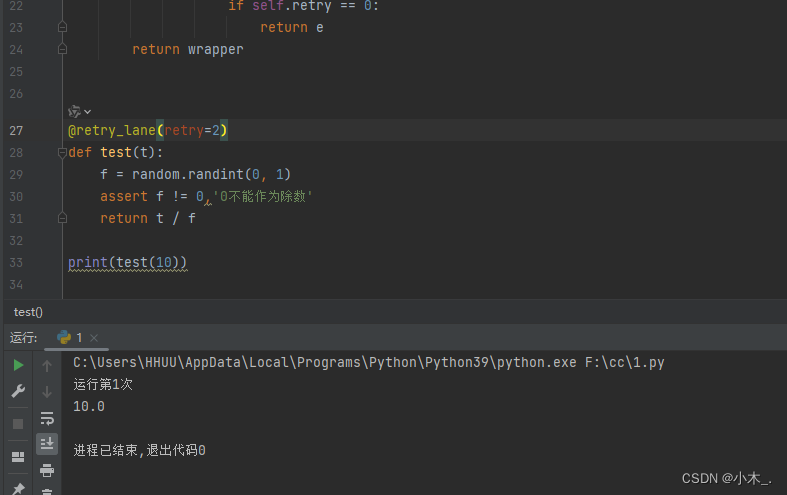
【python 装饰器 - 重试】做一个简易重试装饰器,如果函数执行错误则会自动重新执行,可设置重试次数,对爬虫比较友好
文章日期:2024.03.19 使用工具:Python 类型:装饰器 文章全程已做去敏处理!!! 【需要做的可联系我】 AES解密处理(直接解密即可)(crypto-js.js 标准算法)&…...

Linux线程补充之——同步
一、Linux线程同步 同步是相对于竞争的概念; 同步就是在保证安全的前提下啊,按照一定的顺序访问临界资源; 所有的资源一定是先访问的临界资源,申请失败然后才进行排队的;互斥锁保证的是来访问的进程只允许…...

面试九 设计模式
单例模式通常被归类为创建型设计模式,因为它主要关注如何创建对象的实例,以及如何确保在整个应用程序生命周期中只有一个实例存在。 1.为什么日志模块和数据库连接池需要单例模式 使用单例模式来实现数据库连接池主要有以下几个原因: 全局唯…...

c++和c语言的区别实例
C和C语言在程序设计领域内具有深远的影响,它们不仅丰富了编程的世界,也为软件开发人员提供了强大的工具。虽然C是在C语言的基础上发展起来的,但两者之间存在着一些关键的区别。为了更深入地理解这些不同,本文将从多个维度探讨C和C…...
图论基础|841.钥匙和房间、463. 岛屿的周长
目录 841.钥匙和房间 思路:本题是一个有向图搜索全路径的问题。 只能用深搜(DFS)或者广搜(BFS)来搜。 463. 岛屿的周长 841.钥匙和房间 力扣题目链接 (opens new window) 有 N 个房间,开始时你位于 0…...
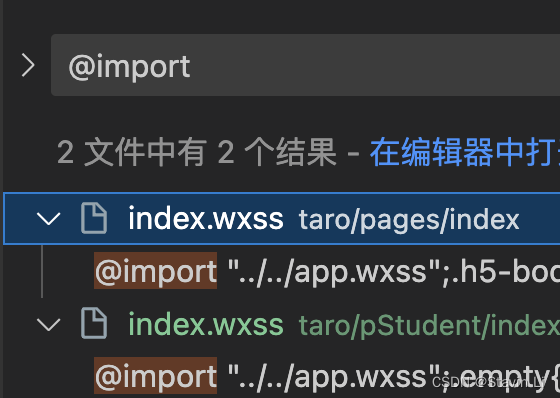
把 Taro 项目作为一个完整分包,Taro项目里分包的样式丢失
现象: 当我们把 Taro 项目作为原生微信小程序一个完整分包时,Taro项目里分包的样式丢失,示意图如下: 原因: 在node_modules/tarojs/plugin-indie/dist/index.js文件里,限制了只有pages目录下会被引入app.w…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

Visual Studio Code 扩展
Visual Studio Code 扩展 change-case 大小写转换EmmyLua for VSCode 调试插件Bookmarks 书签 change-case 大小写转换 https://marketplace.visualstudio.com/items?itemNamewmaurer.change-case 选中单词后,命令 changeCase.commands 可预览转换效果 EmmyLua…...

阿里云Ubuntu 22.04 64位搭建Flask流程(亲测)
cd /home 进入home盘 安装虚拟环境: 1、安装virtualenv pip install virtualenv 2.创建新的虚拟环境: virtualenv myenv 3、激活虚拟环境(激活环境可以在当前环境下安装包) source myenv/bin/activate 此时,终端…...

【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖,添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...
