c#矩阵求逆
目录
一、矩阵求逆的数学方法
1、伴随矩阵法
2、初等变换法
3、分块矩阵法
4、定义法
二、矩阵求逆C#代码
1、伴随矩阵法求指定3*3阶数矩阵的逆矩阵
(1)伴随矩阵数学方法
(2)代码
(3)计算
2、对任意阶数矩阵求逆
(1)计算方法
(2)代码
(3)计算
(4)计算结果
三、工程下载连接
一、矩阵求逆的数学方法
1、伴随矩阵法

2、初等变换法

3、分块矩阵法

4、定义法

二、矩阵求逆C#代码
1、伴随矩阵法求指定3*3阶数矩阵的逆矩阵
(1)伴随矩阵数学方法

(2)代码
/// <summary>/// 计算3*3矩阵的逆矩阵/// </summary>/// <param name="input">输入的3*3矩阵</param>/// <returns>计算得到的3*3逆矩阵</returns>public static double[,] inv3(double[,] input){double[,] output = new double[3, 3];//求出伴随矩阵output[0, 0] = input[2, 2] * input[1, 1] - input[2, 1] * input[1, 2];output[0, 1] = input[2, 1] * input[0, 2] - input[0, 1] * input[2, 2];output[0, 2] = input[0, 1] * input[1, 2] - input[0, 2] * input[1, 1];output[1, 0] = input[1, 2] * input[2, 0] - input[2, 2] * input[1, 0];output[1, 1] = input[2, 2] * input[0, 0] - input[0, 2] * input[2, 0];output[1, 2] = input[0, 2] * input[1, 0] - input[0, 0] * input[1, 2];output[2, 0] = input[1, 0] * input[2, 1] - input[2, 0] * input[1, 1];output[2, 1] = input[2, 0] * input[0, 1] - input[0, 0] * input[2, 1];output[2, 2] = input[0, 0] * input[1, 1] - input[1, 0] * input[0, 1];//求出行列式的值double Avalue = input[0, 0] * input[1, 1] * input[2, 2]+ input[0, 1] * input[1, 2] * input[2, 0]+ input[0, 2] * input[1, 0] * input[2, 1]- input[0, 2] * input[1, 1] * input[2, 0]- input[0, 1] * input[1, 0] * input[2, 2]- input[0, 0] * input[1, 2] * input[2, 1];//求出 逆矩阵 for (int i = 0; i < 3; i++){for (int j = 0; j < 3; j++){output[i, j] = output[i, j] / Avalue;}}return output;}(3)计算
计算代码
计算3*3矩阵的逆矩阵double[,] input = new double[3, 3] {{ 0, 1, 3 }, { 1, -1, 0 },{-1, 2, 1}};double[,] out1 = inv3(input); //方法1——只能求3*3程序计算结果

对应数学题目

2、对任意阶数矩阵求逆
(1)计算方法
Step1
1)利用初等行变换,那么要将单位矩阵E和n阶矩阵B合并(规定为EandB_normal[ n, 2 * n])
Step2
2)将EandB_normal[ n, 2 * n]转为右半部分为上三角的矩阵
>>>这一步转换比较复杂一点,具体实现就是:
>>>第一层循环,循环变量 j 从第n列开始到第2 * n - 1列结束,目的就是将该列值都转为1,方便后边变为上三角矩阵(需要注意的是,对于第n列,应该考虑把每个值都变为1;但是到第n + 1列时,就不考虑第一个值了;第n + 2列时,不考虑第一个和第二个值;类推);
>>>第二层循环,循环变量 i 从第j - n行开始到第n - 1行结束,目的是对每一行都进行除以EandB_normal[ i, j]值的运算,这样EandB_normal[ i, j]的值就变为了1(需要注意的是,如果EandB_normal[ i, j]的值为0的话,我们考虑将该行与最后一行调换,同时循环变量 i 到第n - 2行结束;如果调换之后,EandB_normal[ i, j]的值仍然为0,那么再将该行与此时的最后一行调换,类推;但是如果一直调换,直到发现始终为0,就说明矩阵B不满秩,退出计算;如果EandB_normal[ i, j]值为负数,该行同时变号);
>>>第三层循环,循环变量 k 从第0列开始到第2 * n - 1列结束,目的是将上一步中循环到的行中的每一个值都除以EandB_normal[ i, j]的值;
>>>循环全部完成之后,矩阵EandB_normal[ n, 2 * n]就变成了右半部分为上三角的矩阵。
Step3
3)接上一步,将该矩阵转为右半部分为单位矩阵的矩阵,此时即为矩阵B的逆矩阵与单位矩阵的合并(规定为B_inverse_andE[ n, 2 * n])
>>>这一步中的循环变量是递减的,具体实现就是:
>>>第一层循环,循环变量 j 从第2 * n - 1列开始到第n列结束,目的是将该列值只保留一个1,其余变为0;
>>>第二层循环,循环变量 i 从第 j - n行开始到第0行结束;
>>>第三层循环,循环变量 k 从第0列开始到第2 * n - 1列结束;拿 j = 2 * n - 1, i = n - 1举例,此时,我们希望第n - 2行的值都加上该行最后一个值的相反数与第n - 1行乘积的对应值,第n - 3行的值都加上该行最后一个值得相反数与第n - 1行乘积的对应值,类推;(需要注意的是,j = 2 * n - 2时,i从第n - 2行开始循环,j = 2 * n - 3时,i从第n - 2行开始循环,类推);
>>>当循环全部完成之后,B_inverse_andE[ n, 2 * n]的右半部分就变为了单位矩阵,左半部分为矩阵B的逆矩阵。
Step4
4)接上一步,将B的逆矩阵取出来(规定为B_inverse[n, n])
(2)代码
/// <summary>/// 任意矩阵求逆。(矩阵是2*2、3*3、4*4、5*5等类型)/// </summary>/// <param name="matrixB">输入的初始矩阵</param>/// <param name="orderNum">矩阵行和列的数</param>/// <returns>计算出的逆矩阵</returns>public static double[,] MatrixInverse(double[,] matrixB, int orderNum){//判断是否满秩bool IsFullRank = true;//n为阶级int n = orderNum;//####赋值####//矩阵B//矩阵B的逆矩阵//单位矩阵E和矩阵B组成的矩阵double[,] B_normal = matrixB;double[,] B_inverse = new double[n, n];double[,] EandB_normal = new double[n, 2 * n];for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){if (i == j)EandB_normal[i, j] = 1;elseEandB_normal[i, j] = 0;}for (int k = n; k < 2 * n; k++){EandB_normal[i, k] = B_normal[i, k - n];}}//####计算####//中间变量数组,用于临时盛装值double[] rowHaveZero = new double[2 * n];//EB矩阵右边的n*n变为上三角矩阵for (int j = n; j < 2 * n; j++){int firstRowN = j - n;int lastRowN = n;int colCount = 2 * n;//把EB中索引为j的列的值化为1for (int i = firstRowN; i < lastRowN; i++){//如果EBijNum值为0,就把0所在的行与此刻最后一行调换位置//并且循环变量i的终止值减去1,直到EBijNum值不为0//最多调换到0所在的行的下一行double EBijNum = EandB_normal[i, j];while (EBijNum == 0 && lastRowN > i + 1){for (int k = 0; k < colCount; k++){rowHaveZero[k] = EandB_normal[i, k];EandB_normal[i, k] = EandB_normal[lastRowN - 1, k];EandB_normal[lastRowN - 1, k] = rowHaveZero[k];}lastRowN -= 1;EBijNum = EandB_normal[i, j];}//如果while循环是由第二个判断跳出//即EBijNum始终为0if (EBijNum == 0){//循环变量i的终止值再减去1,然后跳出循环lastRowN -= 1;break;}//如果为负数,该行变号if (EBijNum < 0){for (int k = 0; k < colCount; k++){EandB_normal[i, k] = (-1) * EandB_normal[i, k];}EBijNum = EandB_normal[i, j];}//将该值变为1,则其余值都除以EBijNumfor (int k = 0; k < colCount; k++){EandB_normal[i, k] = EandB_normal[i, k] / EBijNum;}}//自n列起,每列只保留一个1,呈阶梯状int secondRowN = firstRowN + 1;for (int i = secondRowN; i < lastRowN; i++){for (int k = 0; k < colCount; k++){EandB_normal[i, k] = EandB_normal[i, k]- EandB_normal[firstRowN, k];}}if (lastRowN == firstRowN){//矩阵不满秩IsFullRank = false;break;}}//不满秩,结束运算if (!IsFullRank){double[,] error = new double[n, n];for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){error[i, j] = 0;}}//返还值均为0的矩阵return error;}//将上三角矩阵变为单位矩阵for (int j = 2 * n - 1; j > n; j--){//firstRowN为参考行//secondRowN为运算行int firstRowN = j - n;int secondRowN = firstRowN - 1;int colCount = j + 1;//从最后一列起,每列只保留一个1,其余减为0for (int i = secondRowN; i > -1; i--){double EBijNum = EandB_normal[i, j];for (int k = 0; k < colCount; k++){EandB_normal[i, k] = EandB_normal[i, k]- EandB_normal[firstRowN, k] * EBijNum;}}}//####提取逆矩阵####for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){B_inverse[i, j] = EandB_normal[i, j];}}return B_inverse;}
(3)计算
private void button1_Click(object sender, EventArgs e){计算3*3矩阵的逆矩阵double[,] input = new double[3, 3] {{ 0, 1, 3 }, { 1, -1, 0 },{-1, 2, 1}};double[,] out1 = inv3(input); //方法1——只能求3*3double[,] out2 = MatrixInverse(input, 3); //方法2计算2*2矩阵的逆矩阵double[,] input2 = new double[2, 2] {{ 1, 2 }, { 3, 4 }};double[,] out3 = MatrixInverse(input2, 2); //计算4*4矩阵的逆矩阵double[,] input3 = new double[4, 4] {{ 2, 1,-1,2 }, { 1, 1,1,-1 },{0,0,2,5},{0,0,1,3}};double[,] out4 = MatrixInverse(input3, 4); }(4)计算结果
以4*4矩阵说明

三、工程下载连接
https://download.csdn.net/download/panjinliang066333/89024543
相关文章:

c#矩阵求逆
目录 一、矩阵求逆的数学方法 1、伴随矩阵法 2、初等变换法 3、分块矩阵法 4、定义法 二、矩阵求逆C#代码 1、伴随矩阵法求指定3*3阶数矩阵的逆矩阵 (1)伴随矩阵数学方法 (2)代码 (3)计算 2、对…...
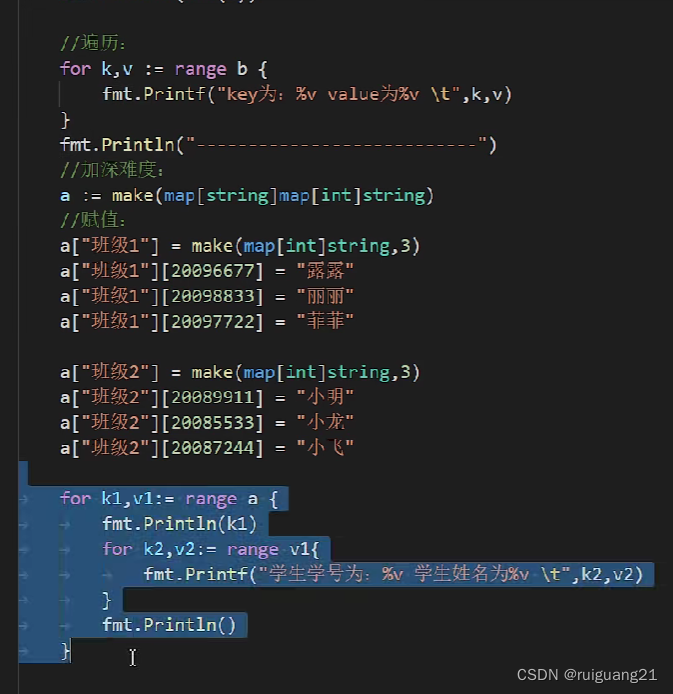
array go 语言的数组 /切片
内存地址通过& package mainimport "fmt"func main() {var arr [2][3]int16fmt.Println(arr)fmt.Printf("arr的地址是: %p \n", &arr)fmt.Printf("arr[0]的地址是 %p \n", &arr[0])fmt.Printf("arr[0][0]的地址是 %p \n"…...
)
【Stable Diffusion】专栏介绍和文章索引(持续更新中)
目录 1 背景2 思考3 文章索引(持续更新中)3.1 入门3.2 初级3.3 中级3.3 高级 1 背景 最近开始学习AIGC,对Stable Diffusion比较感兴趣,所以新建了这个专栏,来记录自己在使用和学习Stable Diffusion的一些方法、资料以…...

RPC 快速入门
一、What 1)小故事 张三和李四都在同一个家公司负责商品交易的模块,两个人平时开发甚是紧密。 🙋🏻♂️ 张三:“李四,我这边一个商品下单了,但是付款数额不对,你帮我查下支付有没…...

使用Docker搭建Syslog-ng
Syslog-ng是一个可靠、多功能的日志管理系统,用于收集日志并将其转发到指定的日志分析工具。 使用Docker CLI方式搭建 步骤 1: 拉取Syslog-ng镜像 首先,需要从Docker Hub拉取Syslog-ng的官方镜像。 docker pull balabit/syslog-ng:latest步骤 2: 启动…...
使能 Linux 内核自带的 FlexCAN 驱动
一. 简介 前面一篇文章学习了 ALPHA开发板修改CAN的设备树节点信息,并加载测试过设备树文件,文件如下: ALPHA开发板修改CAN的设备树节点信息-CSDN博客 本文是学习使能 IMX6ULL的 CAN驱动,也就是通过内核配置来实现。 二. 使能…...

通过dbeaver链接dm8数据库
一、环境说明 windows 11 vmware 17 ubuntu 22 tt:~$ lsb_release -a No LSB modules are available. Distributor ID: Ubuntu Description: Ubuntu 22.04.3 LTS Release: 22.04 Codename: jammytt:~$ docker info Client:Version: 24.0.5Context: d…...
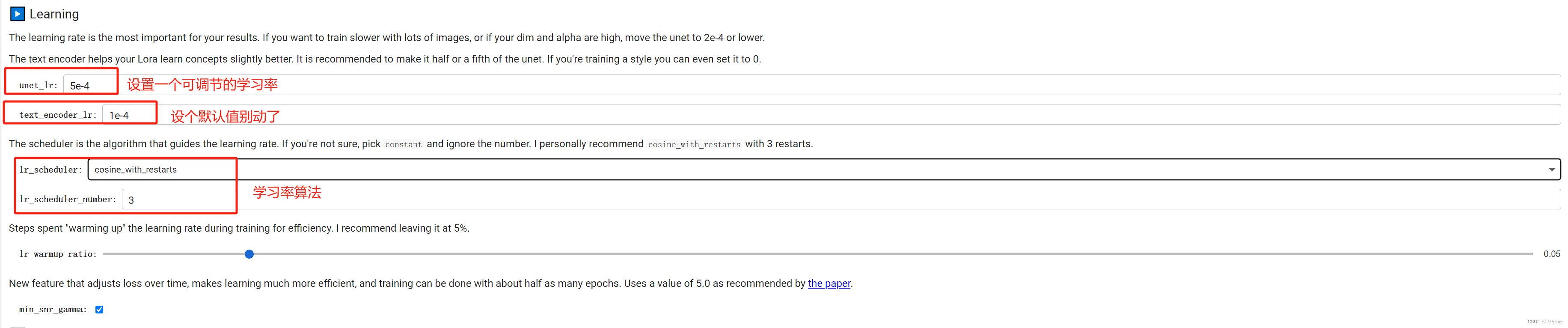
Stable diffusion(四)
训练自己的Lora 【DataSet】【Lora trainer】【SD Lora trainer】 前置的知识 batch size:模型一次性处理几张图片。一次性多处理图片,模型能够综合捕捉多张图片的特征,最终的成品效果可能会好。但是处理多个batch size也意味着更大的显存…...

oracle 19c RAC补丁升级
1.停止集群件备份家目录 ----两节点分别操作 cd /u01/app/19.3.0/grid/bin/ crsctl stop crstar -zcvf /u01/app.tar.gz /u01/app/u01/app/19.0.0/grid/bin/crsctl start crs2.两节点 GI、DB OPatch 替换(都得执行) ----# 表示 root 用户,$…...

计算机视觉研究方向
计算机视觉是一个广泛且快速发展的领域,涵盖了多种研究方向和技术。主要的研究方向包括图像处理、目标检测与识别、图像生成、三维视觉、行为识别、深度学习与计算机视觉、多媒体分析、视频理解、风格化、全向视觉传感器等。这些研究方向和技术不断进步,…...

数据分析-Pandas分类数据的比较如何避坑
数据分析-Pandas分类数据的比较如何避坑 数据分析和处理中,难免会遇到各种数据,那么数据呈现怎样的规律呢?不管金融数据,风控数据,营销数据等等,莫不如此。如何通过图示展示数据的规律? 数据表…...

P - Beat
题目分析 1.看数据范围,大概知道dfs能做 2.自0问题开始查找,确保之后每次查找到的问题的困难度均大于上一次 3.遍历所有情况再记录cnt即可 代码 #include <iostream> #include <algorithm> #include <cstdio> #include <cstring&…...

机器学习——GBDT算法
机器学习——GBDT算法 在机器学习领域,梯度提升决策树(Gradient Boosting Decision Trees,简称GBDT)是一种十分强大且常用的集成学习算法。它通过迭代地训练决策树来不断提升模型性能,是一种基于弱学习器的提升算法。…...
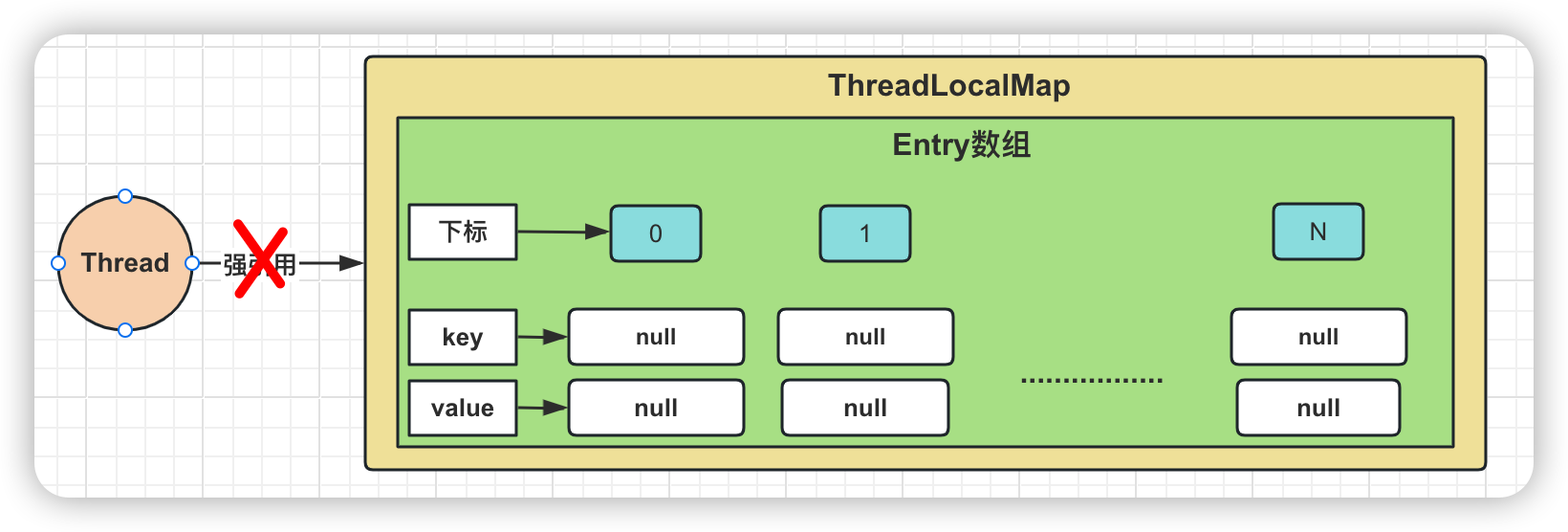
阿里二面:谈谈ThreadLocal的内存泄漏问题?问麻了。。。。
引言 ThreadLocal在Java多线程编程中扮演着重要的角色,它提供了一种线程局部存储机制,允许每个线程拥有独立的变量副本,从而有效地避免了线程间的数据共享冲突。ThreadLocal的主要用途在于,当需要为每个线程维护一个独立的上下文…...

IOS面试题编程机制 46-50
46. 阐述 Method Swizzle(黑魔法),什么情况下会使用?1). 在没有一个类的实现源码的情况下,想改变其中一个方法的实现,除了继承它重写、和借助类别重名方法暴力抢先之外,还有更加灵活的方法 Method Swizzle。 2). Method Swizzle 指的是改变一个已存在的选择器对应的实现…...
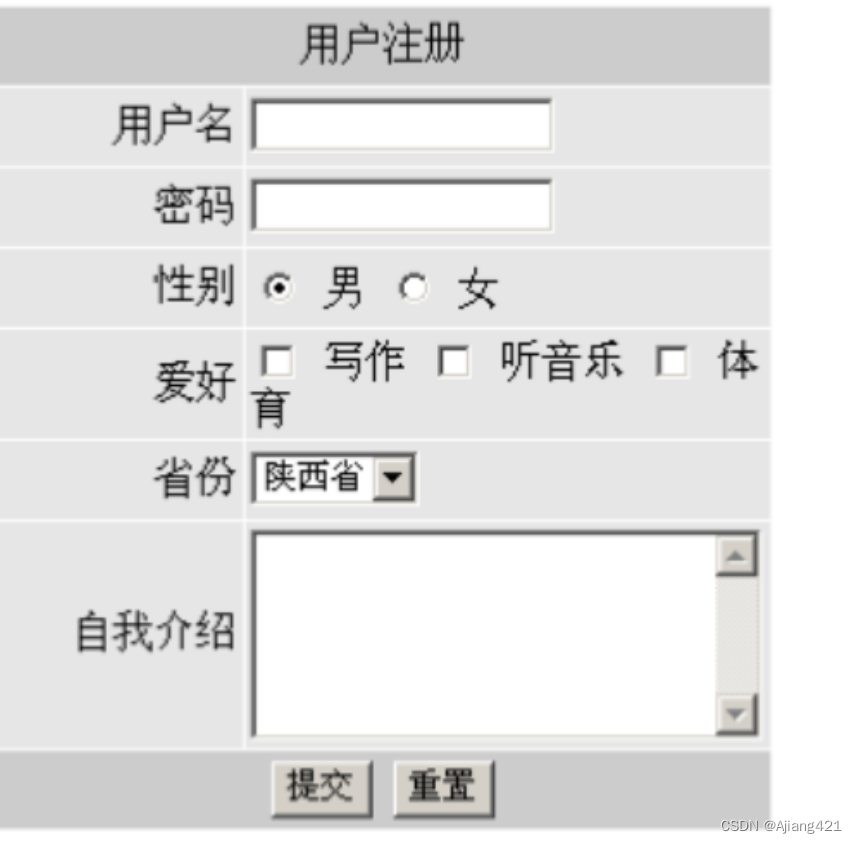
web表单标签与练习(3.18)
一、表单域 表单域是一个包含表单元素的区域。 在HTML标签中,< form >标签用于定义表单域,以实现用户信息和传递。 < form >会把它范围内的表单元素信息提交给服务器。 表单属性 action url地址 用于指定接收并处理表单数据的服务器程序的…...
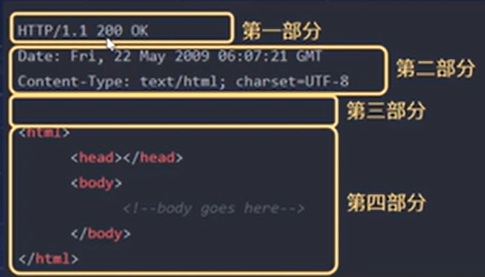
【协议-HTTP】
HTTP协议 HTTP协议(超文本传输协议HyperText Transfer Protocol),它是基于TCP协议的应用层传输协议。http协议定义web客户端如何才能够web服务器请求web页面,以及服务器如何把web页面传送给客户端。 HTTP 是一种无状态 (stateless) 协议, HTTP协议本身…...

VUE3v-text、v-html、:style的理解
在Vue 3中,v-text、v-html和:style是三个常用的指令,它们各自具有不同的功能和用途。 v-text: v-text用于操作元素中的纯文本内容。它接受一个表达式,并将该表达式的值设置为元素的文本内容。如果元素原本有文本内容,…...
的简介、安装、案例应用之详细攻略)
Dataset之UCI_autos_cars:UCI_autos_imports-85(汽车进口数据集)的简介、安装、案例应用之详细攻略
Dataset之UCI_autos_cars:UCI_autos_imports-85(汽车进口数据集)的简介、安装、案例应用之详细攻略 目录 UCI_autos_imports-85的简介 UCI_autos_imports-85的安装 UCI_autos_imports-85的案例应用 1、训练一个简单的线性回归模型来预测汽车的价格 UCI_autos_i…...
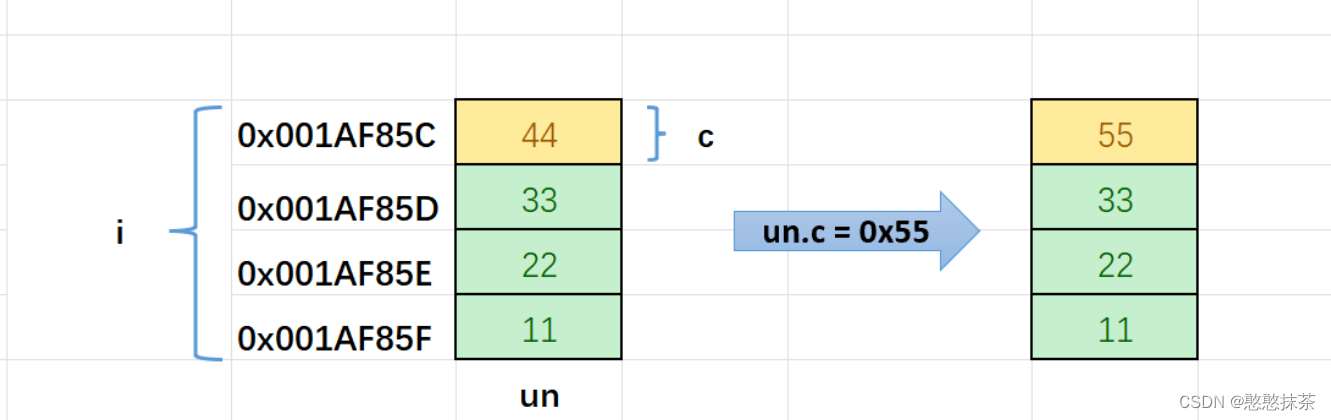
结构体类型详细讲解(附带枚举,联合)
前言: 如果你还对结构体不是很了解,那么本篇文章将会从 为什么存在结构体,结构体的优点,结构体的定义,结构体的使用与结构体的大小依次介绍,同样会附带枚举与联合体 目录 为什么存在结构体: 结构…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...
