Stable diffusion（四）
训练自己的Lora
【DataSet】【Lora trainer】【SD Lora trainer】
前置的知识
- batch size：模型一次性处理几张图片。一次性多处理图片，模型能够综合捕捉多张图片的特征，最终的成品效果可能会好。但是处理多个batch size也意味着更大的显存。同时batch size和Step的关系也是相反的。多batch size意味着每张图片能分到的step变小了。
- Epoch轮数。重复训练几轮的意思。
- Step：步数。 Step = 图片数量 * 重复次数(repeat) * 轮数(epoch) ÷ batch size。距离，假设你有50张图片，每张图片的repeat设置为10次，训练10个epoch。那么 Step = 50 * 10 * 10 ÷ 2= 2500步。
- Learning rate：学习率就代表着收敛的速度。我建议是可变的学习率，前面几个step大点，后面几个step小点。常见的学习率调整算法
- Learning rate scheduler：
- Optimizer：优化器，这个后面进阶再去了解
- network alpho：缩放因子防止模型过拟合
- network dim ：模型的层数 network alpho推荐设置为 netwrok dim的一半。
- Lora的选型
- warnup：warmup是针对学习率learning rate优化的一种策略，主要过程是，在预热期间，学习率从0线性（也可非线性）增加到优化器中的初始预设lr，之后使其学习率从优化器中的初始lr线性降低到0
界面介绍
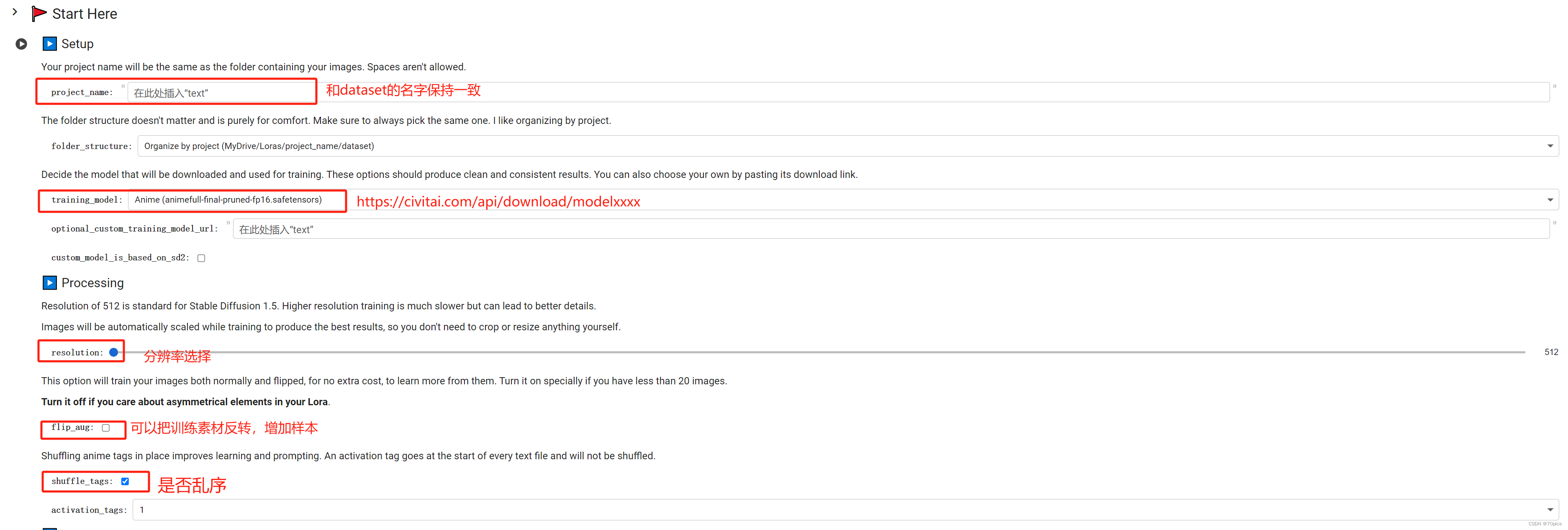
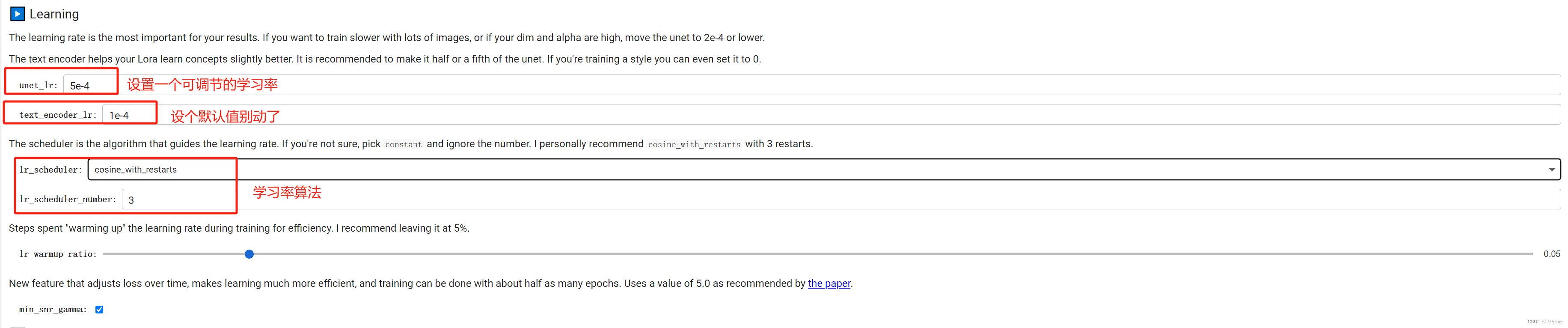
如何完成自己的DataSet
因为自己练出的Lora实在太丑，愤而不写了。不如用别人的
相关文章：
Stable diffusion（四）
训练自己的Lora 【DataSet】【Lora trainer】【SD Lora trainer】 前置的知识 batch size：模型一次性处理几张图片。一次性多处理图片，模型能够综合捕捉多张图片的特征，最终的成品效果可能会好。但是处理多个batch size也意味着更大的显存…...
oracle 19c RAC补丁升级
1.停止集群件备份家目录 ----两节点分别操作 cd /u01/app/19.3.0/grid/bin/ crsctl stop crstar -zcvf /u01/app.tar.gz /u01/app/u01/app/19.0.0/grid/bin/crsctl start crs2.两节点 GI、DB OPatch 替换（都得执行） ----# 表示 root 用户，$…...
计算机视觉研究方向
计算机视觉是一个广泛且快速发展的领域，涵盖了多种研究方向和技术。主要的研究方向包括图像处理、目标检测与识别、图像生成、三维视觉、行为识别、深度学习与计算机视觉、多媒体分析、视频理解、风格化、全向视觉传感器等。这些研究方向和技术不断进步，…...
数据分析-Pandas分类数据的比较如何避坑
数据分析-Pandas分类数据的比较如何避坑 数据分析和处理中，难免会遇到各种数据，那么数据呈现怎样的规律呢？不管金融数据，风控数据，营销数据等等，莫不如此。如何通过图示展示数据的规律？ 数据表…...
P - Beat
题目分析 1.看数据范围，大概知道dfs能做 2.自0问题开始查找，确保之后每次查找到的问题的困难度均大于上一次 3.遍历所有情况再记录cnt即可 代码 #include <iostream> #include <algorithm> #include <cstdio> #include <cstring&…...
机器学习——GBDT算法
机器学习——GBDT算法 在机器学习领域，梯度提升决策树（Gradient Boosting Decision Trees，简称GBDT）是一种十分强大且常用的集成学习算法。它通过迭代地训练决策树来不断提升模型性能，是一种基于弱学习器的提升算法。…...
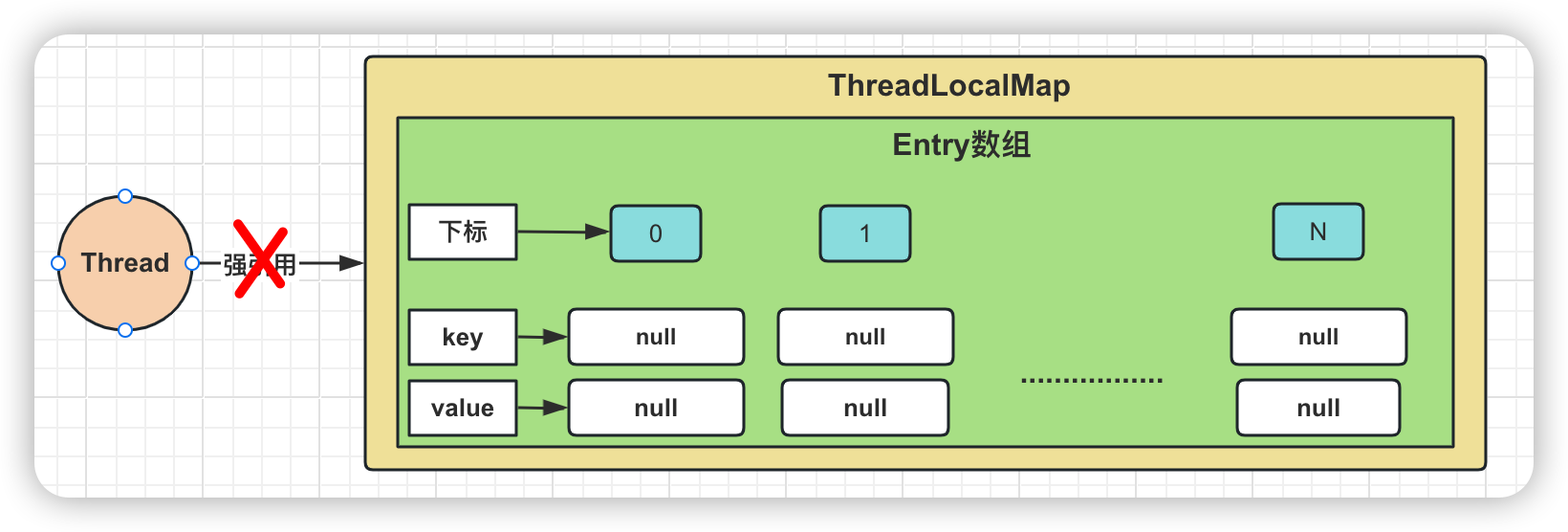
阿里二面：谈谈ThreadLocal的内存泄漏问题？问麻了。。。。
引言 ThreadLocal在Java多线程编程中扮演着重要的角色，它提供了一种线程局部存储机制，允许每个线程拥有独立的变量副本，从而有效地避免了线程间的数据共享冲突。ThreadLocal的主要用途在于，当需要为每个线程维护一个独立的上下文…...
IOS面试题编程机制 46-50
46. 阐述 Method Swizzle（黑魔法），什么情况下会使用？1). 在没有一个类的实现源码的情况下，想改变其中一个方法的实现，除了继承它重写、和借助类别重名方法暴力抢先之外，还有更加灵活的方法 Method Swizzle。 2). Method Swizzle 指的是改变一个已存在的选择器对应的实现…...
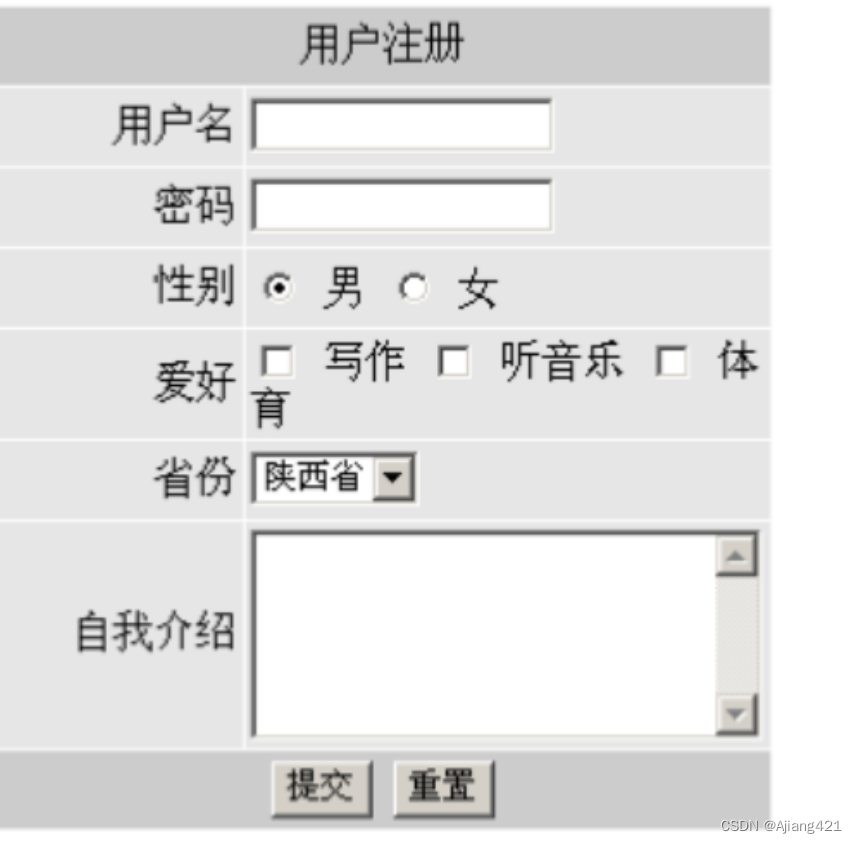
web表单标签与练习（3.18）
一、表单域 表单域是一个包含表单元素的区域。 在HTML标签中，< form >标签用于定义表单域，以实现用户信息和传递。 < form >会把它范围内的表单元素信息提交给服务器。 表单属性 action url地址 用于指定接收并处理表单数据的服务器程序的…...
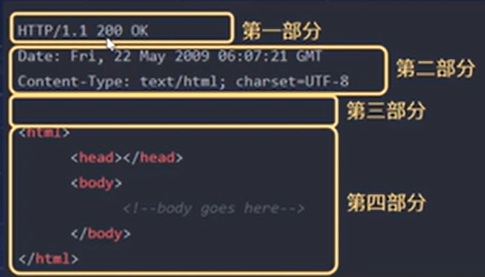
【协议-HTTP】
HTTP协议 HTTP协议(超文本传输协议HyperText Transfer Protocol)，它是基于TCP协议的应用层传输协议。http协议定义web客户端如何才能够web服务器请求web页面，以及服务器如何把web页面传送给客户端。 HTTP 是一种无状态 (stateless) 协议, HTTP协议本身…...
VUE3v-text、v-html、:style的理解
在Vue 3中，v-text、v-html和:style是三个常用的指令，它们各自具有不同的功能和用途。 v-text： v-text用于操作元素中的纯文本内容。它接受一个表达式，并将该表达式的值设置为元素的文本内容。如果元素原本有文本内容，…...
的简介、安装、案例应用之详细攻略)
Dataset之UCI_autos_cars：UCI_autos_imports-85(汽车进口数据集)的简介、安装、案例应用之详细攻略
Dataset之UCI_autos_cars：UCI_autos_imports-85(汽车进口数据集)的简介、安装、案例应用之详细攻略 目录 UCI_autos_imports-85的简介 UCI_autos_imports-85的安装 UCI_autos_imports-85的案例应用 1、训练一个简单的线性回归模型来预测汽车的价格 UCI_autos_i…...
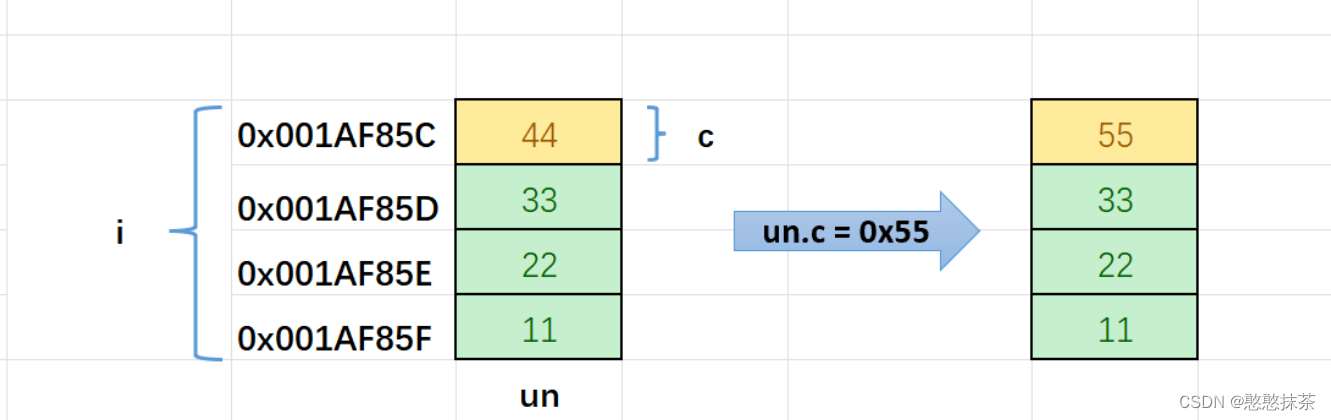
结构体类型详细讲解（附带枚举，联合）
前言： 如果你还对结构体不是很了解，那么本篇文章将会从 为什么存在结构体，结构体的优点，结构体的定义，结构体的使用与结构体的大小依次介绍，同样会附带枚举与联合体 目录 为什么存在结构体： 结构…...
编程生活day1--个位数统计、考试座位号、A-B、计算阶乘和
个位数统计 题目描述： 定一个 k 位整数 Ndk−110k−1⋯d1101d0 (0≤di≤9, i0,⋯,k−1, dk−1>0)，请编写程序统计每种不同的个位数字出现的次数。例如：给定 N100311，则有 2 个 0，3 个 1，和 …...
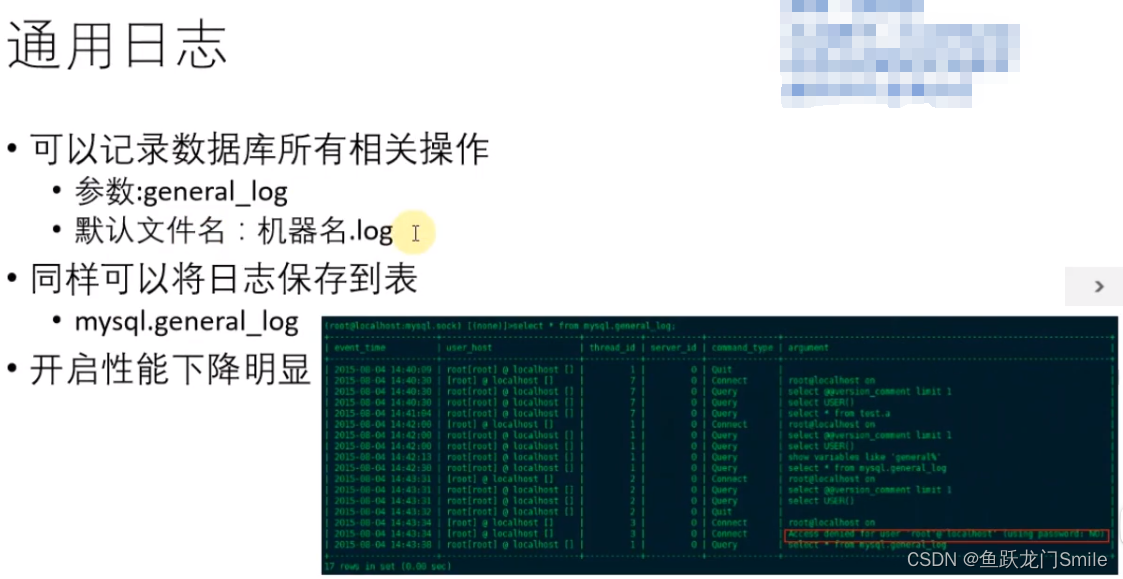
mysql体系结构及主要文件
目录 1.mysql体系结构 2.数据库与数据库实例 3.物理存储结构编辑 4.mysql主要文件 4.1数据库配置文件 4.2错误日志 4.3表结构定义文件 4.4慢查询日志 4.4.1慢查询相关参数 4.4.2慢查询参数默认值 4.4.3my.cnf中设置慢查询参数 4.4.4slow_query_log参数 4.4.…...
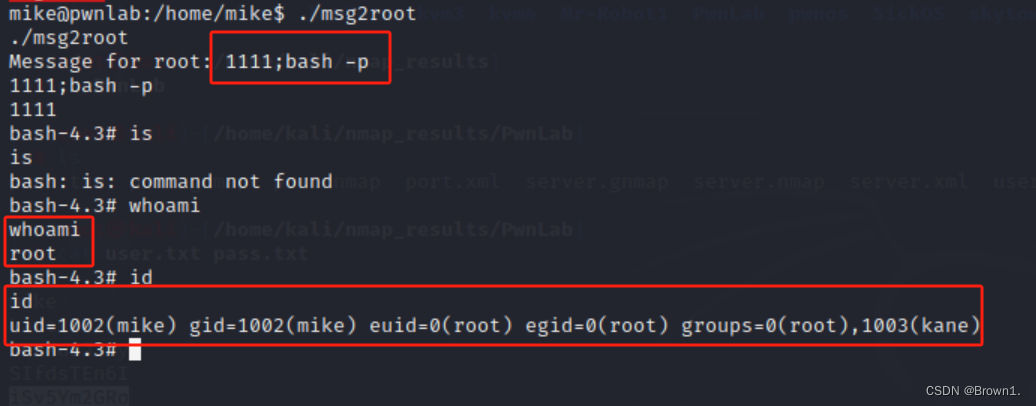
PwnLab靶场PHP伪协议OSCP推荐代码审计命令劫持命令注入
下载链接：PwnLab: init ~ VulnHub 安装： 打开vxbox直接选择导入虚拟电脑即可 正文： 先用nmap扫描靶机ip nmap -sn 192.168.1.1/24 获取到靶机ip后，对靶机的端口进行扫描，并把结果输出到PwnLab文件夹下，命名…...
涉密信息系统集成资质八大类别办理条件是什么？
涉密资质分为八个不同类别，那每个类别的申报条件有哪些？让我们一起来看看吧： 涉密资质申报条件 依据《涉密信息系统集成资质管理办法》的有关规定，申请涉密信息系统集成资质的企事业单位，除符合《涉密信息系统集成资…...
)
Shell脚本总结-反引号-${}-$()
反引号 反引号的作用就是将输出结果显示出来。 [rootldpbzhaonan bash]$ echo $a ldpbzhaonan${} ${}引用变量，包含自定义的和环境变量。 [rootldpbzhaonan bash]$ a1 [rootldpbzhaonan bash]$ echo ${a} 1$() $()和反引号，返回的是一个指令或者程序…...
Spring MVC入门(4)
请求 获取Cookie/Session 获取Cookie 传统方式: RequestMapping("/m11")public String method11(HttpServletRequest request, HttpServletResponse response) {//获取所有Cookie信息Cookie[] cookies request.getCookies();//打印Cookie信息StringBuilder build…...
RuoYi-Vue-Plus（基础知识点jackson、mybatisplus、redis）
一、JacksonConfig 全局序列化反序列化配置 1.1yml中配置 #时区 spring.jackson.time-zoneGMT8 #日期格式 spring.jackson.date-formatyyyy-MM-dd HH:mm:ss #默认转json的属性，这里设置为非空才转json spring.jackson.default-property-inclusionnon_null #设置属性…...
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造，完美适配AGV和无人叉车。同时，集成以太网与语音合成技术，为各类高级系统（如MES、调度系统、库位管理、立库等）提供高效便捷的语音交互体验。 L…...
Zustand 状态管理库：极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库，特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...
逻辑回归：给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告（肿瘤大小、血液指标），你需要做出一个**决定性判断**：恶性还是良性？这种“非黑即白”的抉择，正是**逻辑回归（Logistic Regression）** 的战场&a…...
关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述：iview使用table 中type: "index",分页之后 ，索引还是从1开始，试过绑定后台返回数据的id, 这种方法可行，就是后台返回数据的每个页面id都不完全是按照从1开始的升序，因此百度了下，找到了…...
在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...
以光量子为例，详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学（silicon photonics）的光波导（optical waveguide）芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中，光既是波又是粒子。光子本…...
HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架，允许使用简单的变成模型跨计算机对大型集群进行分布式处理（1.海量的数据存储 2.海量数据的计算）Hadoop核心组件 hdfs（分布式文件存储系统）&a…...
算法：模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣（LeetCode） 遍历字符串：通过外层循环逐一检查每个字符。遇到 ? 时处理： 内层循环遍历小写字母（a 到 z）。对每个字母检查是否满足： 与…...
A2A JS SDK 完整教程：快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...
纯 Java 项目（非 SpringBoot）集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目（非 SpringBoot）集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...