深度学习pytorch——多分类问题(持续更新)
回归问题 vs 分类问题(regression vs classification)
回归问题(regression)
1、回归问题的目标是使预测值等于真实值,即pred=y。
2、求解回归问题的方法是使预测值和真实值的误差最小,即minimize dist(pred,y),一般我们通过求其2-范数,再平方得到它的最小值,也可以直接使用1-范数。
分类问题(classification)
1、分类问题的目标是找到最大的概率,即maximize benchmark(accurcy)。
2、求解分类问题,第一种方法是找到真实值与预测值之间的最小距离,即minimize dist( p(y | x), pr(y | x) )。第二种方法是找到真实值与预测值的最小差异,即minimize divergence( p
(y | x), pr(y | x) )
但是,为什么不直接就概率呢?
1、如果概率不发生改变,权重发生改变,就会导致梯度等于0,出现梯度离散的现象。
2、由于正确的数量是不连续的,因此造成梯度也是不连续的,会导致梯度爆炸、训练不稳定等问题。
二分类问题(Binary Classification)
给定一个函数 f :x ---> p(y = 1 | x),如果二分类的角度去研究这个问题。预测的方法是:如果p(y = 1 | x) > 0.5 ,则预测值为1,否则预测值为0。
以交叉熵的角度分析二分类问题:
首先将二分类问题实例化,是对于猫和狗的分类问题,根据概率之和等于1,我们可以得到狗的概率等于1减去猫的概率,即P(dog) = (1 - P(cat)),接着将其带入到交叉熵公式中,得到以下公式:
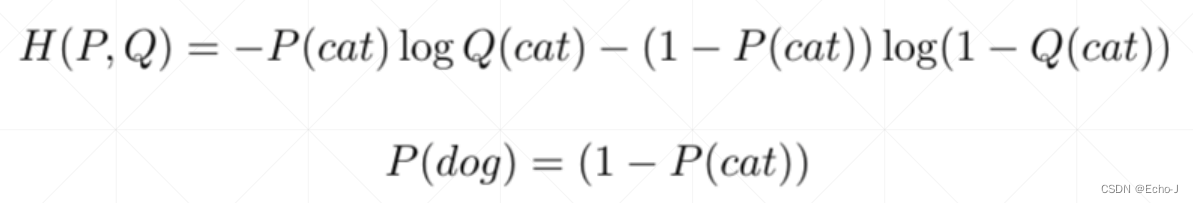
将具体问题扩展到 一般问题,得到如下公式:

分析以上公式,当y = 1 时,H (P, Q) = log(p);当y = 0 时,H (P, Q) = log(1 - p);这两种情况随着p的变化,单调性是相反的,进一步证明了交叉熵解决二分类问题的可行性。
多分类问题(Multi-class classification)
给定一个函数 f :x ---> p(y | x) ,其中 [𝑝 𝑦 = 0 𝑥 , 𝑝 𝑦 = 1 𝑥 , … , 𝑝 𝑦 = 9 𝑥 。必须满足:所有的𝑝 (𝑦 |𝑥) ∈ [0, 1];所有的概率和 𝑝 (𝑦 = 𝑖 |𝑥 )= 1。
如何让所有的概率和为1呢?
使用softmax函数,详情请看深度学习pytorch——激活函数&损失函数(持续更新)-CSDN博客
交叉熵(cross entropy)
1、交叉熵的特点:
(1)具有很高的不确定性
(2)度量很惊喜
2、交叉熵的公式:

3、交叉熵的值越高就代表不稳定性越大
(1)以代码的方式解释
可以清楚的观察到数据的分布越平衡,最后得到的熵值就越高,反之,熵值就越低。
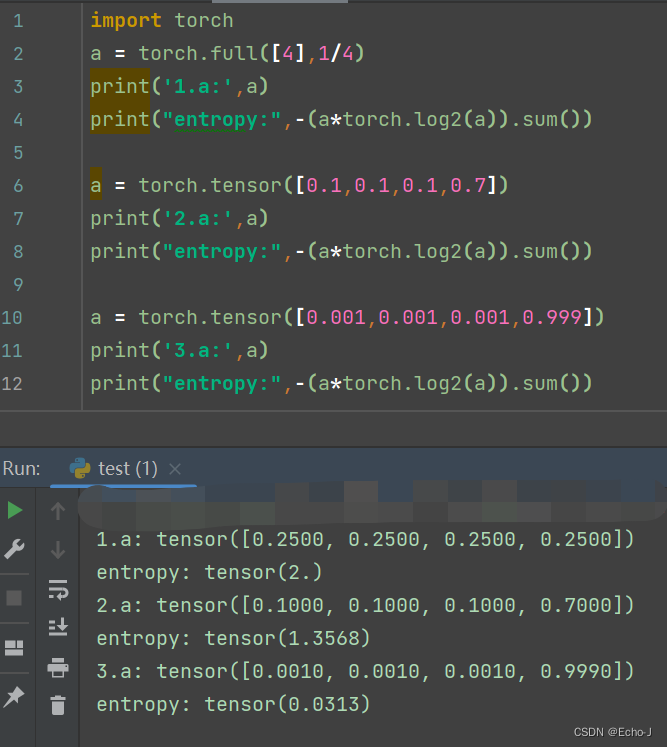
import torch
a = torch.full([4],1/4)
print('1.a:',a)
print("entropy:",-(a*torch.log2(a)).sum())a = torch.tensor([0.1,0.1,0.1,0.7])
print('2.a:',a)
print("entropy:",-(a*torch.log2(a)).sum())a = torch.tensor([0.001,0.001,0.001,0.999])
print('3.a:',a)
print("entropy:",-(a*torch.log2(a)).sum())(2)以理论的角度解释
给出Cross Entropy 的公式:

当Cross Entropy 和Entropy 这两个分布相等时,即H(p,q)=H(p),此时两个分布重合,此时Dkl就等于0。
当使用one-hot加密,我们可以得到Entropy = 1log1 = 0,即H(p)= 0,则此时满足H(p, q) = Dkl(p|q)的情况,此时如果对H(p,q)进行优化,相当于将Dkl(p|q)直接优化了,这是我们直接可以不断减小Dkl(p|q)的值,使预测值逐渐接近真实值,这就很好的解释了我们为什么要使用Cross Entropy。
为什么不使用MSE?
1、sigmoid + MSE 的模式会导致梯度离散的现象
2、收敛速度比较慢
通过下图可以很合理的证明以上两个原因的合理性:
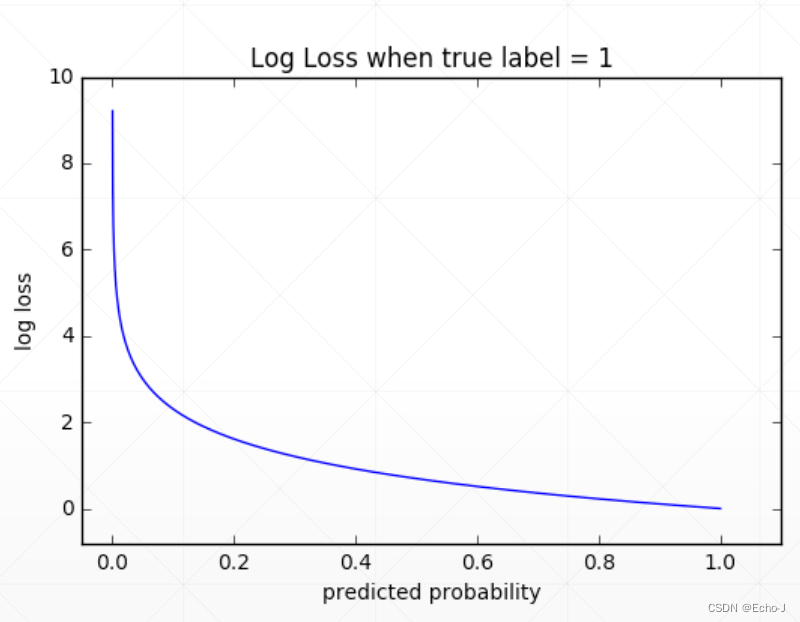
3、但是有时我们再做一些前沿的技术时,会发现MSE效果要好于cross entropy,因为它的求解梯度较为简单。
MSE VS Cross Entropy
Cross Entropy = sofymax + log + nll_loss,最后的结果都是一样的。
import torch
from torch.nn import functional as F
# MSE vs Cross Entropy
x = torch.randn(1,784)
w = torch.randn(10,784)
logists = x@w.t()
# 使用Cross Entropy
print(F.cross_entropy(logists,torch.tensor([3])))
# tensor(0.0194)
# 自己处理
pred = F.softmax(logists, dim = 1)
pred_log = torch.log(pred)
print(F.nll_loss(pred_log,torch.tensor([3])))
# tensor(0.0194)多分类问题实战
############# Logistic Regression 多分类实战(MNIST)###########
# (1)加载数据
# (2)定义网络
# (3)凯明初始化
# (4)training:实例化一个网络对象,构建优化器,迭代,定义loss,输出
# (5)testingimport torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transformsbatch_size=200 #Batch Size:一次训练所选取的样本数
learning_rate=0.01
epochs=10 #1个epoch表示过了1遍训练集中的所有样本,这里可以设置为 5# 加载数据
train_loader = torch.utils.data.DataLoader(datasets.MNIST('../data', train=True, download=True,transform=transforms.Compose([transforms.ToTensor(),transforms.Normalize((0.1307,), (0.3081,))])),batch_size=batch_size, shuffle=True)
test_loader = torch.utils.data.DataLoader(datasets.MNIST('../data', train=False, transform=transforms.Compose([transforms.ToTensor(),transforms.Normalize((0.1307,), (0.3081,))])),batch_size=batch_size, shuffle=True)# 在pytorch中的定义(a,b)a是ch-out输出,b是ch-in输入,也就是(输出,输入)
# 比如第一个可以理解为从784降维成200的层
w1, b1 = torch.randn(200, 784, requires_grad=True),\torch.zeros(200, requires_grad=True)
w2, b2 = torch.randn(200, 200, requires_grad=True),\torch.zeros(200, requires_grad=True)
w3, b3 = torch.randn(10, 200, requires_grad=True),\torch.zeros(10, requires_grad=True)# 凯明初始化,如果不进行初始化会出现梯度离散的现象
# torch.nn.init.kaiming_normal_(tensor, a=0, mode='fan_in', nonlinearity='leaky_relu')
torch.nn.init.kaiming_normal_(w1)
torch.nn.init.kaiming_normal_(w2)
torch.nn.init.kaiming_normal_(w3)# 前向传播过程
def forward(x):x = x@w1.t() + b1x = F.relu(x)x = x@w2.t() + b2x = F.relu(x)x = x@w3.t() + b3x = F.relu(x) #这里千万不要用softmax,因为之后的crossEntropyLoss中自带了。这里可以用relu,也可以不用。return x #返回的是一个logits(即没有经过sigmoid或者softmax的层)# 优化器
optimizer = optim.SGD([w1, b1, w2, b2, w3, b3], lr=learning_rate)
criteon = nn.CrossEntropyLoss()for epoch in range(epochs):for batch_idx, (data, target) in enumerate(train_loader):data = data.view(-1, 28*28) # 将二维的图片数据打平 [200,784],第5课用的 x = x.view(x.size(0), 28*28)logits = forward(data) #这里是网络的输出loss = criteon(logits, target) # 调用cross—entorpy计算输出值和真实值之间的lossoptimizer.zero_grad()loss.backward()# print(w1.grad.norm(), w2.grad.norm())optimizer.step()# 每 batch_idx * 100=20000输出结果 每100个bachsize打印输出的结果,看看loss的情况if batch_idx % 100 == 0:print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(epoch, batch_idx * len(data), len(train_loader.dataset),100. * batch_idx / len(train_loader), loss.item()))# len(data)---指的是一个batch_size;
# len(train_loader.dataset)----指的是train_loader这个数据集中总共有多少张图片(数据)
# len(train_loader)---- len(train_loader.dataset)/len(data)---就是这个train_loader要加载多少次batch# 测试网络---test----每训练完一个epoch检测一下测试结果# 因为每一个epoch已经优化了batch次参数,得到的参数信息还是OK的test_loss = 0correct = 0for data, target in test_loader:data = data.view(-1, 28 * 28)logits = forward(data) #logits的shape=[200,10],--200是batchsize,10是最后输出结果的10分类test_loss += criteon(logits, target).item() #每次将test_loss进行累加 #target=[200,1]---每个类只有一个正确结果pred = logits.data.max(1)[1]# 这里losgits.data是一个二维数组;其dim=1;max()---返回的是每行的最大值和最大值对应的索引# max(1)----是指每行取最大值;max(1)[1]---取每行最大值对应的索引号# 也可以写成 pred=logits.argmax(dim=1)correct += pred.eq(target.data).sum()#预测值和目标值相等个数进行求和--在for中,将这个test_loader中相等的个数都求出来test_loss /= len(test_loader.dataset)print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(test_loss, correct, len(test_loader.dataset),100. * correct / len(test_loader.dataset)))"""
影响training的因素有:
1、learning rate过大
2、gradient vanish---梯度弥散(参数梯度为0,导致loss保持为常数,loss长时间得不到更新)
3、初始化问题----参数初始化问题
"""课时50 多分类问题实战_哔哩哔哩_bilibili
相关文章:

深度学习pytorch——多分类问题(持续更新)
回归问题 vs 分类问题(regression vs classification) 回归问题(regression) 1、回归问题的目标是使预测值等于真实值,即predy。 2、求解回归问题的方法是使预测值和真实值的误差最小,即minimize dist(p…...
)
Flutter探索之旅:控制键盘可见性的神奇工具(flutter_keyboard_visibility)
随着移动应用的不断发展,用户体验的重要性愈发突显。而键盘的弹出和隐藏对于用户体验来说是至关重要的一环。在Flutter中,我们有幸拥有一个强大的工具——flutter_keyboard_visibility,它让我们能够轻松地监测键盘的可见性并做出相应的响应。…...
提升质量透明度,动力电池企业的数据驱动生产实践 | 数据要素 × 工业制造
系列导读 如《“数据要素”三年行动计划(2024—2026年)》指出,工业制造是“数据要素”的关键领域之一。如何发挥海量数据资源、丰富应用场景等多重优势,以数据流引领技术流、资金流、人才流、物资流,对于制造企业而言…...

华为数通 HCIP-Datacom H12-831 题库补充
2024年 HCIP-Datacom(H12-831)最新题库,完整题库请扫描上方二维码,持续更新。 缺省情况下,PIM报文的IP协议号是以下哪一项? A:18 B:59 C:103 D:9 答案&a…...

tensorflow中显存分配
tensorflow中显存分配 问题:使用tensorflow-gpu训练模型,GPU的显存都是占满的。 # GPU 1的显存将占满 os.environ["CUDA_VISIBLE_DEVICES"] "1" 原因:默认情况下,tensorflow会把可用的显存全部占光&#…...
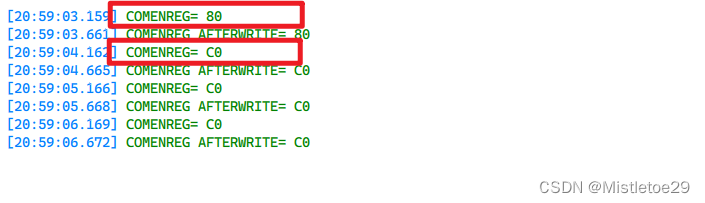
STM32--RC522学习记录
一,datasheet阅读记录 1.关于通信格式 2.读寄存器 u8 RC522_ReadReg(u8 address) {u8 addr address;u8 data0x00;addr((addr<<1)&0x7e)|0x80;//将最高位置一表示read,最后一位按照手册建议变为0Spi_Start();//选中从机SPI2_ReadWriteByte(ad…...

函数封装冒泡排序
大家好: 衷心希望各位点赞。 您的问题请留在评论区,我会及时回答。 一、冒泡排序 冒泡排序是最常见的一种排序算法,按照指定顺序比较相邻元素,如果顺序不同,就交换元素位置,每一趟比较,都会导致…...
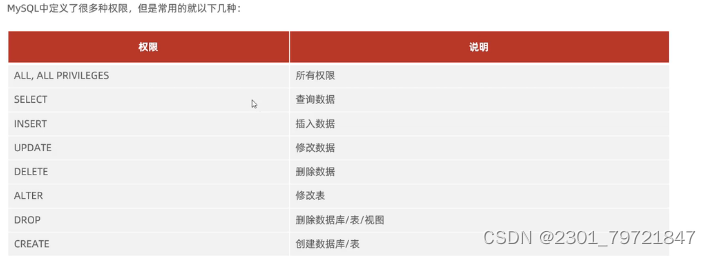
mysql基础学习
一、DML 介绍:DML(数据操作语言),用来对数据库中表的数据记录进行增删改操作。 1.添加数据 /*给指定字段添加数据*/ insert into user(id, name) values (1,小王); select *from user;/*查询该表的数据*/ /*给所有字段添数据*/ insert int…...

mybatisplus提示:Property ‘mapperLocations‘ was not specified.
1、问题概述? 在使用springboot整么mybatisPlus启动的使用提示信息: Property mapperLocations was not specified. 但是我确实写了相对应的配置: 【在pom文件中配置xml识别】 <resources><resource><directory>src/m…...

【STL源码剖析】【2、空间配置器——allocator】
文章目录 1、什么是空间配置器?1.1设计一个简单的空间配置器,JJ::allocator 2、具备次配置力( sub-allocation)的 SGI 空间配置器2.1 什么是次配置力2.2 SGI标准的空间配置器,std::allocator2.2 SGI特殊的空间配置器,std::alloc2.…...

机器人|逆运动学问题解决方法总结
如是我闻: 解决逆运动学(Inverse Kinematics, IK)问题的方法多样,各有特点。以下是一个综合概述: 1. 解析法(Analytical Solutions) 特点:直接使用数学公式计算关节角度࿰…...
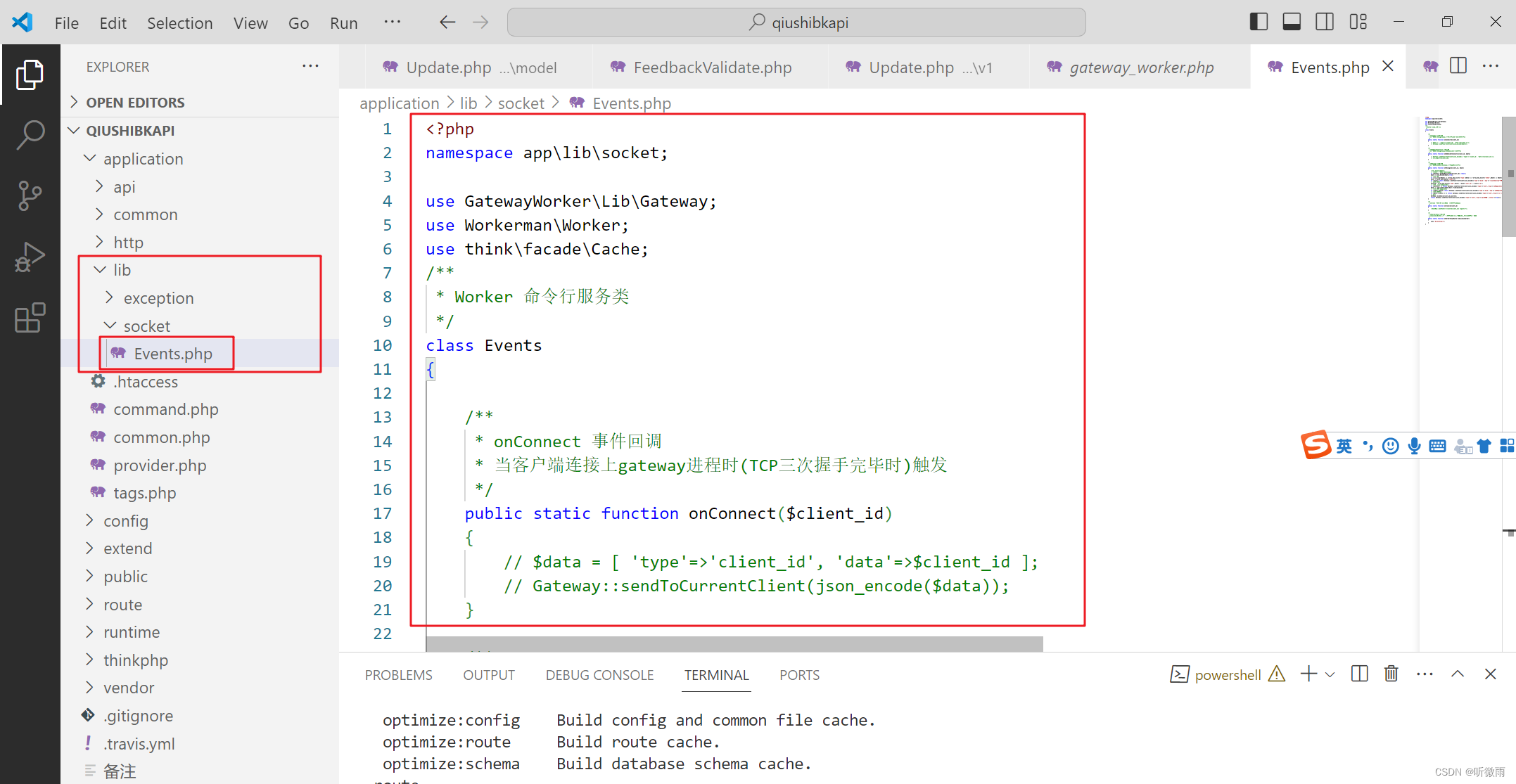
php搭建websocket
workerman文档:https://www.workerman.net/doc/gateway-worker/unbind-uid.html 1.项目终端执行命令:composer require topthink/think-worker 2.0.x 2.config多出三个配置文件: 3.当使用php think worker:gateway命令时,提示不…...

maven install报错原因揭秘:‘parent.relativePath‘指向错误的本地POM文件
哈喽,大家好,我是木头左! 今天我要和大家分享的是关于maven install时报错的一个常见原因:parent.relativePath’指向错误的本地POM文件。这个问题可能会影响到的开发效率,甚至导致项目构建失败。那么,该如…...
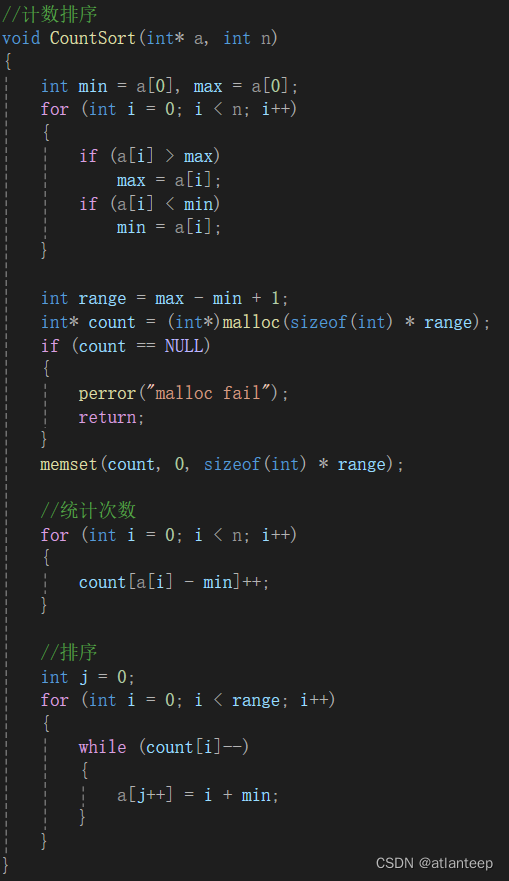
数据结构·排序
1. 排序的概念及运用 1.1 排序的概念 排序:排序是将一组“无序”的记录序列,按照某个或某些关键字的大小,递增或递减归零调整为“有序”的记录序列的操作 稳定性:假定在待排序的记录序列中,存在多个具有相同关键字的记…...

Python学习笔记01
第一章、你好Python 初识Python Python的起源 1989年,为了打发圣诞节假期,Gudiovan Rossum吉多范罗苏姆(龟叔)决心开发一个新的解释程序(Python雏形) 1991年,第一个Python解释器诞生 Python这个名字,来自龟叔所挚爱的电视剧M…...

Java学习笔记01
1.1 Java简介 Java的前身是Oak,詹姆斯高斯林是java之父。 1.2 Java体系 Java是一种与平台无关的语言,其源代码可以被编译成一种结构中立的中间文件(.class,字节码文件)于Java虚拟机上运行。 1.2.3 专有名词 JDK提…...

SOC子模块---RTC and watchdog
RTC RTC大致执行过程: 对SOC 中的锁相环或者外部晶振的时钟进行计数;产生时,分,秒的中断;送给中断控制器;中断控制器进行优先权选择后送给cpu;Cpu执行中断服务程序;在中断服务程序…...

【测试开发学习历程】MySQL增删改操作 + 备份与还原 + 索引、视图、存储过程
前言: SQL内容的连载,到这里就是最后一期啦! 如果有小伙伴要其他内容的话,我会追加内容的。(前提是我有学过,或者能学会) 接下来,我们就要开始python内容的学习了 ~ ~ 目录 1 …...
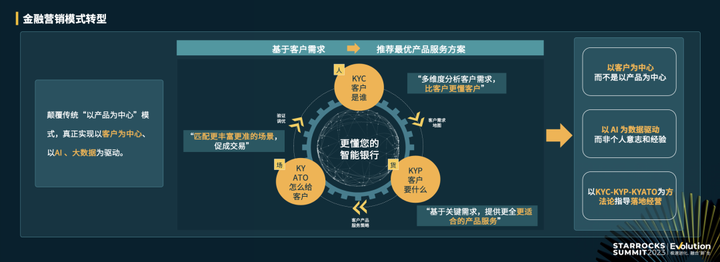
StarRocks 助力金融营销数字化进化之路
作者:平安银行 数据资产中心数据及 AI 平台团队负责人 廖晓格 平安银行五位一体,做零售金融的领先银行,五位一体是由开放银行、AI 银行、远程银行、线下银行、综合化银行协同构建的数据化、智能化的零售客户经营模式,这套模式以数…...
医院预约挂号系统设计与实现|jsp+ Mysql+Java+ Tomcat(可运行源码+数据库+设计文档)
本项目包含可运行源码数据库LW,文末可获取本项目的所有资料。 推荐阅读100套最新项目 最新ssmjava项目文档视频演示可运行源码分享 最新jspjava项目文档视频演示可运行源码分享 最新Spring Boot项目文档视频演示可运行源码分享 2024年56套包含java,…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...
