【二十三】【算法分析与设计】三柱汉诺塔详解,计算子移动次数,正常递归计算,观察数据得出数学规律,递归图得出数学规律,将递归函数转化为递推式
目录
汉诺塔递归
汉诺塔子移动次数的计算
牛牛的汉诺塔
选择正常的递归模拟计算子移动次数
根据具体数据得出数学规律
根据递归图得出数学规律
将递归函数转化为递推式
结尾
汉诺塔递归
汉诺塔是一个经典问题,相传在古印度圣庙中,有一种被称为汉诺塔(Hanoi)的游戏。该游戏是在一块铜板装置上,有三根杆(编号A、B、C),在A杆自下而上、由大到小按顺序放置n个金盘。游戏的目标:把A杆上的金盘全部移到C杆上,并仍保持原有顺序叠好。操作规则:每次只能移动一个盘子,并且在移动过程中三根杆上都始终保持大盘在下,小盘在上,操作过程中盘子可以置于A、B、C任一杆上。
汉诺塔以及其衍生问题往往使用递归来求解,也是学习和理解递归很好的老师。
其伪代码如下
Function Hanoi(n,a,b,c)if n==1 thenprint(a+'->'+c)elseHanoi(n-1,a,c,b)print(a+'->'+c)Hanoi(n-1,b,a,c)end if
end Function 定义递归函数hanoi(n,a,b,c)表示将n个盘子从a柱移动到c柱,以b柱为辅助柱。
维护定义的含义,内部逻辑先将n-1个盘子从a柱移动到b柱,以c柱为辅助柱。再将最大盘子从a柱移动到c柱,以b柱为辅助柱。最后将n-1个盘子从b柱移动到c柱,以a柱为辅助柱。
递归结束出口为n==1时,从a柱移动到c柱,以b柱为辅助柱。
C++代码
#include <iostream>
using namespace std;// 函数声明
void hanoi(int n, char a, char b, char c) {if (n == 1) {cout << a << "->" << c<< endl;return;}hanoi(n-1, a, c, b);cout << a << " -> " << c<< endl;hanoi(n-1, b, a, c);
}
汉诺塔子移动次数的计算
牛牛的汉诺塔
链接:登录—专业IT笔试面试备考平台_牛客网 来源:牛客网
时间限制:C/C++ 1秒,其他语言2秒
空间限制:C/C++ 262144K,其他语言524288K
64bit IO Format: %lld
题目描述
汉诺塔是一个经典问题,相传在古印度圣庙中,有一种被称为汉诺塔(Hanoi)的游戏。该游戏是在一块铜板装置上,有三根杆(编号A、B、C),在A杆自下而上、由大到小按顺序放置n个金盘。游戏的目标:把A杆上的金盘全部移到C杆上,并仍保持原有顺序叠好。操作规则:每次只能移动一个盘子,并且在移动过程中三根杆上都始终保持大盘在下,小盘在上,操作过程中盘子可以置于A、B、C任一杆上。
汉诺塔以及其衍生问题往往使用递归来求解,也是学习和理解递归很好的老师。
其伪代码如下
Function Hanoi(n,a,b,c)
if n==1 then
print(a+'->'+c)
else
Hanoi(n-1,a,c,b)
print(a+'->'+c)
Hanoi(n-1,b,a,c)
end if
end Function
牛牛很快就理解了代码的意思并且写出了求解汉诺塔的程序,他现在想研究汉诺塔的规律。
请你统计以下信息:A->B,A->C,B->A,B->C,C->A,C->B的次数,以及所有移动的总步数。
输入描述:
仅一行,输入一个正整数n(1≤n≤60)(1 leq n leq 60)(1≤n≤60)表示汉诺塔的层数。
输出描述:
首先输出6行
A->B:XX
A->C:XX
B->A:XX
B->C:XX
C->A:XX
C->B:XX
分别表示每种移动情况出现的次数
最后输出一行
SUM:XX
表示所有移动情况的总和。
示例1
输入
复制3
3
输出
复制A->B:1 A->C:3 B->A:1 B->C:1 C->A:0 C->B:1 SUM:7
A->B:1
A->C:3
B->A:1
B->C:1
C->A:0
C->B:1
SUM:7
说明
伪代码所示算法的移动序列如下:
A->C
A->B
C->B
A->C
B->A
B->C
A->C
统计:
A->B出现1次
A->C出现3次
B->C出现1次
B->A出现1次
C->B出现1次
总计7次
选择正常的递归模拟计算子移动次数
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
LL N = 1000005;
LL MOD = 1e4 + 7;
LL N1 = 10005;void Hanoi(int n, char a, char b, char c, int& count_ab, int& count_ac, int& count_ba, int& count_bc, int& count_ca, int& count_cb) {if (a == 'A' && c == 'B') count_ab++;if (a == 'A' && c == 'C') count_ac++;if (a == 'B' && c == 'A') count_ba++;if (a == 'B' && c == 'C') count_bc++;if (a == 'C' && c == 'A') count_ca++;if (a == 'C' && c == 'B') count_cb++;if (n == 1) {return;} else {Hanoi(n - 1, a, c, b, count_ab, count_ac, count_ba, count_bc, count_ca, count_cb);Hanoi(n - 1, b, a, c, count_ab, count_ac, count_ba, count_bc, count_ca, count_cb);}
}
int main() {int count_ab = 0;int count_ac = 0;int count_ba = 0;int count_bc = 0;int count_ca = 0;int count_cb = 0;char a = 'A', b = 'B', c = 'C';int n;cin>>n;Hanoi(n, a, b, c, count_ab, count_ac, count_ba, count_bc, count_ca, count_cb);int count=count_ab+count_ac+count_ba+count_bc+count_ca+count_cb;cout<<"A->B:"<<count_ab<<endl;cout<<"A->C:"<<count_ac<<endl;cout<<"B->A:"<<count_ba<<endl;cout<<"B->C:"<<count_bc<<endl;cout<<"C->A:"<<count_ca<<endl;cout<<"C->B:"<<count_cb<<endl;cout<<"SUM:"<<count;
}我们可以通过递归关系式来表达这个问题的解法次数。对于n个盘子,移动它们所需的步骤T(n)可以表示为:
T(n)=2T(n−1)+1
这里的思路是:移动n-1个盘子到临时柱子(这需要T(n-1)步),移动最大的盘子到目标柱子(这需要1步),最后再将n-1个盘子从临时柱子移动到目标柱子上(再次需要T(n-1)步)。
我们可以进一步解开这个递归式:
-
当
n = 1时,只需要移动一次,所以T(1) = 1。 -
当
n = 2时,T(2) = 2T(1) + 1 = 3。 -
当
n = 3时,T(3) = 2T(2) + 1 = 7。
以此类推,我们发现这是一个等比数列的求和问题,其总和公式为:
T(n)=2^n−1
因此,汉诺塔问题的时间复杂度为O(2^n)。这个复杂度表明了随着盘子数量的增加,需要的移动次数呈指数级增长,这也解释了为什么汉诺塔问题在盘子数量稍多时就变得难以直接通过手动移动来解决。
当n==60时,时间复杂度是O(2^60),2^10≈1000=10^3,2^60==2^10*2^10*2^10*2^10*2^10*2^10。也就是六个10^3相乘,等于10^18远远超过10^9,10^9对应的时间大概是1s,这样的递归是一定会超时的。
根据具体数据得出数学规律
我们将正常递归模拟计算子移动次数的代码进行修改,用来计算前n项的子移动次数数据。
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
LL N = 1000005;
LL MOD = 1e4 + 7;
LL N1 = 10005;void Hanoi(int n, char a, char b, char c, int& count_ab, int& count_ac, int& count_ba, int& count_bc, int& count_ca, int& count_cb) {if (a == 'A' && c == 'B') count_ab++;if (a == 'A' && c == 'C') count_ac++;if (a == 'B' && c == 'A') count_ba++;if (a == 'B' && c == 'C') count_bc++;if (a == 'C' && c == 'A') count_ca++;if (a == 'C' && c == 'B') count_cb++;if (n == 1) {return;} else {Hanoi(n - 1, a, c, b, count_ab, count_ac, count_ba, count_bc, count_ca, count_cb);Hanoi(n - 1, b, a, c, count_ab, count_ac, count_ba, count_bc, count_ca, count_cb);}}
int main() {char a = 'A', b = 'B', c = 'C';cout<<" ";cout << setw(8) << "a->b " << setw(8) << "a->c " << setw(8) << "b->a " << setw(8) << "b->c " << setw(8) << "c->a " << setw(8) << "c->b " << setw(8) << "SUM " << endl;for (int i = 1; i <= 20; i++) {int count_ab = 0;int count_ac = 0;int count_ba = 0;int count_bc = 0;int count_ca = 0;int count_cb = 0;Hanoi(i, a, b, c, count_ab, count_ac, count_ba, count_bc, count_ca, count_cb);int count = count_ab + count_ac + count_ba + count_bc + count_ca + count_cb;cout << "n="<<setw(2) << i<<":";cout << setw(7) << count_ab << " ";cout << setw(7) << count_ac << " ";cout << setw(7) << count_ba << " ";cout << setw(7) << count_bc << " ";cout << setw(7) << count_ca << " ";cout << setw(7) << count_cb << " ";cout << setw(7) << count << endl;}}//输出a->b a->c b->a b->c c->a c->b SUM
n= 1: 0 1 0 0 0 0 1
n= 2: 1 1 0 1 0 0 3
n= 3: 1 3 1 1 0 1 7
n= 4: 4 3 1 4 2 1 15
n= 5: 4 9 6 4 2 6 31
n= 6: 15 9 6 15 12 6 63
n= 7: 15 31 27 15 12 27 127
n= 8: 58 31 27 58 54 27 255
n= 9: 58 117 112 58 54 112 511
n=10: 229 117 112 229 224 112 1023
n=11: 229 459 453 229 224 453 2047
n=12: 912 459 453 912 906 453 4095
n=13: 912 1825 1818 912 906 1818 8191
n=14: 3643 1825 1818 3643 3636 1818 16383
n=15: 3643 7287 7279 3643 3636 7279 32767
n=16: 14566 7287 7279 14566 14558 7279 65535
n=17: 14566 29133 29124 14566 14558 29124 131071
n=18: 58257 29133 29124 58257 58248 29124 262143
n=19: 58257 116515 116505 58257 58248 116505 524287
n=20: 233020 116515 116505 233020 233010 116505 1048575我们将a->b,a->c,b->a,b->c,c->a,c->b分别记为1,2,3,4,5,6。
我们希望找出前后项的规律,很容易发现,同一个n中,1号等于4号,3号等于6号。
因此我们将数据截取出1,2,3,5四列数据。做法很简单,只需要简单修改代码即可。
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
LL N = 1000005;
LL MOD = 1e4 + 7;
LL N1 = 10005;void Hanoi(int n, char a, char b, char c, int& count_ab, int& count_ac, int& count_ba, int& count_bc, int& count_ca, int& count_cb) {if (a == 'A' && c == 'B') count_ab++;if (a == 'A' && c == 'C') count_ac++;if (a == 'B' && c == 'A') count_ba++;if (a == 'B' && c == 'C') count_bc++;if (a == 'C' && c == 'A') count_ca++;if (a == 'C' && c == 'B') count_cb++;if (n == 1) {return;} else {Hanoi(n - 1, a, c, b, count_ab, count_ac, count_ba, count_bc, count_ca, count_cb);Hanoi(n - 1, b, a, c, count_ab, count_ac, count_ba, count_bc, count_ca, count_cb);}}
int main() {char a = 'A', b = 'B', c = 'C';cout << " ";cout << setw(8) << "a->b ";cout << setw(8) << "a->c ";cout << setw(8) << "b->a ";
// cout << setw(8) << "b->c ";cout << setw(8) << "c->a ";
// cout << setw(8) << "c->b ";cout << setw(8) << "SUM " << endl;for (int i = 1; i <= 20; i++) {int count_ab = 0;int count_ac = 0;int count_ba = 0;int count_bc = 0;int count_ca = 0;int count_cb = 0;Hanoi(i, a, b, c, count_ab, count_ac, count_ba, count_bc, count_ca, count_cb);int count = count_ab + count_ac + count_ba + count_bc + count_ca + count_cb;cout << "n=" << setw(2) << i << ":";cout << setw(7) << count_ab << " ";cout << setw(7) << count_ac << " ";cout << setw(7) << count_ba << " ";
// cout << setw(7) << count_bc << " ";cout << setw(7) << count_ca << " ";
// cout << setw(7) << count_cb << " ";cout << setw(7) << count << endl;}}//输出a->b a->c b->a c->a SUM
n= 1: 0 1 0 0 1
n= 2: 1 1 0 0 3
n= 3: 1 3 1 0 7
n= 4: 4 3 1 2 15
n= 5: 4 9 6 2 31
n= 6: 15 9 6 12 63
n= 7: 15 31 27 12 127
n= 8: 58 31 27 54 255
n= 9: 58 117 112 54 511
n=10: 229 117 112 224 1023
n=11: 229 459 453 224 2047
n=12: 912 459 453 906 4095
n=13: 912 1825 1818 906 8191
n=14: 3643 1825 1818 3636 16383
n=15: 3643 7287 7279 3636 32767
n=16: 14566 7287 7279 14558 65535
n=17: 14566 29133 29124 14558 131071
n=18: 58257 29133 29124 58248 262143
n=19: 58257 116515 116505 58248 524287
n=20: 233020 116515 116505 233010 1048575我们希望由上面的数据找出前后项的关系,我们对a->b,a->c,b->a,c->a重新进行编号,分别记为1,2,3,4。
我们需要用的n-1项的1,2,3,4号数据推导出n项的1,2,3,4号数据。
找规律的思路是,我们可以先关注n项的1号数据,看n-1项的某一号数据是否可以单独推导出n项的1号数据。1对1的关系。如果1对1的关系找不到,那就找n-1项的多号数据是否可以推导出1号数据,以此类推。
先关注n项1号与n-1项一对一的关系。
当n==7时,1号等于n==6的(2号*2-3),等于(3号*2+3)。
当n==8时,1号等于n==7的(2号*2-4),等于(3号*2+4)。
当n==9时,1号等于n==8的(2号*2-4),等于(3号*2+4)。
当n==10时,1号等于n==9的(2号*2-5),等于(3号*2+5)。
很容易发现递推公式,n项的1号等于n-1项的(2号*2-n/2)或者等于(3号*2+n/2)。
找到1号的递推式,我们接着找2号的递推式。
先关注n项2号与n-1项一对一的关系。
当n==7时,2号等于n==6的(1号*2+1)。
当n==8时,2号等于n==7的(1号*2+1)。
当n==9时,2号等于n==8的(1号*2+1)。
当n==10时,2号等于n==9的(1号*2+1)。
很容易发现递推公式,n项的2号等于n-1项的(2号*2+1)。
找到2号的递推式,我们接着找3号的递推式。
先关注n项3号与n-1项一对一的关系。
当n==7时,3号等于n==6的(1号*2-3)。
当n==8时,3号等于n==7的(1号*2-3)。
当n==9时,3号等于n==8的(1号*2-4)。
当n==10时,3号等于n==9的(1号*2-4)。
很容易发现递推公式,n项的3号等于n-1项的(1号*2-(n-1)/2)。
找到3号的递推式,我们接着找4号的递推式。
先关注n项4号与n-1项一对一的关系。
当n==7时,4号等于n==6的(3号*2)。
当n==8时,4号等于n==7的(3号*2)。
当n==9时,4号等于n==8的(3号*2)。
当n==10时,4号等于n==9的(3号*2)。
很容易发现递推公式,n项的4号等于n-1项的(3号*2)。
接着我们就可以利用递推式直接求前后项的数据。
其实我们可以发现,上述的前后项关系不仅仅是上述的几种,例如n项的1号等于n-1项的(1号+2号),n项的3号等于n-1项的(1号+4号)等等。我们知道的是这些推导公式都可以推导出前后项关系,得到递推式。
#include<bits/stdc++.h>
using namespace std;
using LL=long long;
int main(){int n;cin>>n;vector<vector<LL>> a(n+1,vector<LL>(4));a[1][1]=1;for(int i=2;i<=n;i++){a[i][0]=a[i-1][1]+a[i-1][2];a[i][1]=a[i-1][0]*2+1;a[i][2]=a[i-1][3]*2+(i-1)/2;a[i][3]=a[i-1][2]*2;}cout<<"A->B:"<<a[n][0]<<endl;cout<<"A->C:"<<a[n][1]<<endl;cout<<"B->A:"<<a[n][2]<<endl;cout<<"B->C:"<<a[n][0]<<endl;cout<<"C->A:"<<a[n][3]<<endl;cout<<"C->B:"<<a[n][2]<<endl;cout<<"SUM:"<<a[n][0]*2+a[n][1]+a[n][2]*2+a[n][3]<<endl;
}根据递归图得出数学规律

#include <bits/stdc++.h>
using namespace std;
using LL = long long;
int main() {int n;cin >> n;LL count_ab = 0, count_ac = 0, count_ba = 0, count_bc = 0, count_ca = 0, count_cb = 0;LL length = 1;for (int i = 1; i <= n; i++) {if (i != 1)length *= 2;if (i % 2 == 1) {LL tempcount = length / 3;count_ac += tempcount;count_cb += tempcount;count_ba += tempcount;LL tempcount1 = length % 3;if (tempcount1 == 1) {count_ac++;} else {count_ac++;count_cb++;}} else {LL tempcount = length / 3;count_ab += tempcount;count_bc += tempcount;count_ca += tempcount;LL tempcount1 = length % 3;if (tempcount1 == 1) {count_ab++;} else {count_ab++;count_bc++;}}}cout << "A->B:" << count_ab << endl;cout << "A->C:" << count_ac << endl;cout << "B->A:" << count_ba << endl;cout << "B->C:" << count_bc << endl;cout << "C->A:" << count_ca << endl;cout << "C->B:" << count_cb << endl;cout << "SUM:" << count_ab + count_ac + count_ba + count_bc + count_ca + count_cb << endl;
}将递归函数转化为递推式

#include <bits/stdc++.h>
using namespace std;
using LL = long long;
int main() {int n;cin >> n;vector<vector<LL>> dp(3,vector<LL>(7));dp[1][2] = 1;for (int i = 2; i <= n; i++) {dp[2][1] = dp[1][2] + dp[1][3];dp[2][2] = dp[1][1] + dp[1][4] + 1;dp[2][3] = dp[1][1] + dp[1][5];dp[2][4] = dp[1][2] + dp[1][6];dp[2][5] = dp[1][6] + dp[1][3];dp[2][6] = dp[1][5] + dp[1][4];dp[1][1] = dp[2][1];dp[1][2] = dp[2][2];dp[1][3] = dp[2][3];dp[1][4] = dp[2][4];dp[1][5] = dp[2][5];dp[1][6] = dp[2][6];}cout << "A->B:" << dp[1][1] << endl;cout << "A->C:" << dp[1][2] << endl;cout << "B->A:" << dp[1][3] << endl;cout << "B->C:" << dp[1][4] << endl;cout << "C->A:" << dp[1][5] << endl;cout << "C->B:" << dp[1][6] << endl;cout << "SUM:" << dp[1][1] + dp[1][2] + dp[1][3] + dp[1][4] + dp[1][5] + dp[1][6] << endl;
}结尾
最后,感谢您阅读我的文章,希望这些内容能够对您有所启发和帮助。如果您有任何问题或想要分享您的观点,请随时在评论区留言。
同时,不要忘记订阅我的博客以获取更多有趣的内容。在未来的文章中,我将继续探讨这个话题的不同方面,为您呈现更多深度和见解。
谢谢您的支持,期待与您在下一篇文章中再次相遇!
相关文章:

【二十三】【算法分析与设计】三柱汉诺塔详解,计算子移动次数,正常递归计算,观察数据得出数学规律,递归图得出数学规律,将递归函数转化为递推式
目录 汉诺塔递归 汉诺塔子移动次数的计算 牛牛的汉诺塔 选择正常的递归模拟计算子移动次数 根据具体数据得出数学规律 根据递归图得出数学规律 将递归函数转化为递推式 结尾 汉诺塔递归 汉诺塔是一个经典问题,相传在古印度圣庙中,有一种被称为汉…...

C# WPF编程-XAML
C# WPF编程-XAML XAML简述XAML子集XAML编译XAML基础XAML名称空间XAML中的属性和事件属性事件使用其他名称空间中的类型 加载和编译XAML XAML简述 XAML(Extensible Application Markup Language的简写,发音"zammel")是用于实例化.NET对象的标记语言。XAML…...
java 高级面试题(借鉴)(下)
雪花算法原理 第1位符号位固定为0,41位时间戳,10位workId,12位序列号,位数可以有不同实现。 优点:每个毫秒值包含的ID值很多,不够可以变动位数来增加,性能佳(依赖workId的实现…...

C++测试代码
C测试代码 目录 基于C实现的AOP功能 基于C实现的AOP功能 #include <iostream> #include <string>struct LogHeader {std::string prefix;std::string aspect; };template <typename T> void before(const std::string& msg, const LogHeader& heade…...
Flask python 开发篇:蓝图的使用
蓝图 引言一、为什么使用蓝图?二、蓝图的概念三、创建蓝图四、注册蓝图五、分享我的creat_app方法六、写在最后 引言 falsk是个轻量级的框架,核心实现简单,但同事可以让开发人员自由的扩展功能。开发中,使用模块导入的方式。 一…...

抖音视频爬虫下载软件|可导出视频分享链接|视频批量采集工具
无水印视频关键词批量下载工具操作指南 我们自主开发了一款便捷的音视频批量下载工具,不仅支持单个视频链接提取,还可通过关键词搜索实现批量采集和选择性下载,让您轻松获取所需视频内容。 操作说明: 关键词批量采集视频 进入软件…...

CentOS DHCP服务器部署指南
title: DHCP 服务器部署以及配置 search: 2024-03-21 tags: “#DHCP 服务器部署以及配置” CentOS DHCP 服务器部署指南 背景 :因上了 Linux 的实验课程,在课程中,老师要求我们自己搭建 DHCP 服务器构建局域网,在构建的时候问题百…...
llvm后端
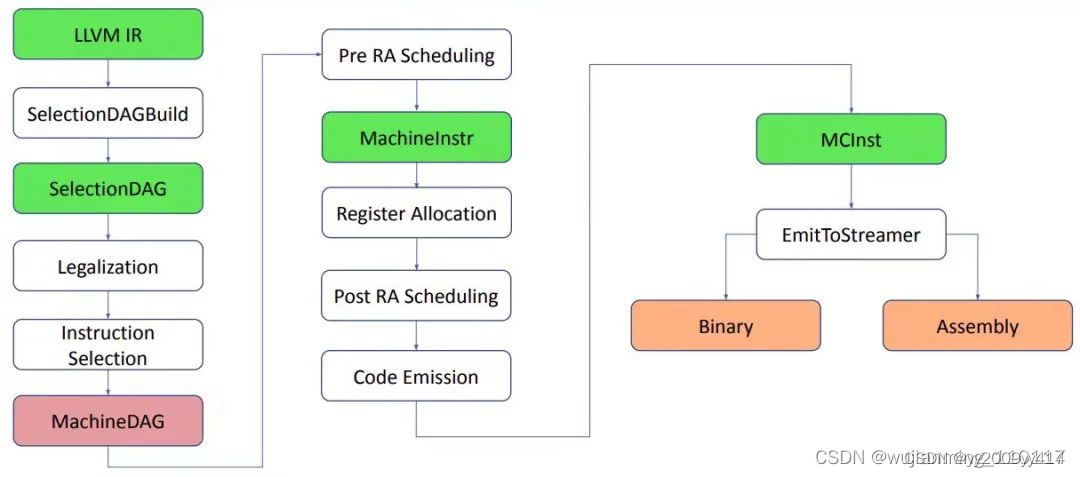
SelectionDAGBuilder是LLVM(Low Level Virtual Machine)编译器中的一个重要组件,它负责将LLVM中间表示(Intermediate Representation,IR)转换为SelectionDAG(选择有向无环图)的形式。…...
【JSON2WEB】10 基于 Amis 做个登录页面login.html
【JSON2WEB】01 WEB管理信息系统架构设计 【JSON2WEB】02 JSON2WEB初步UI设计 【JSON2WEB】03 go的模板包html/template的使用 【JSON2WEB】04 amis低代码前端框架介绍 【JSON2WEB】05 前端开发三件套 HTML CSS JavaScript 速成 【JSON2WEB】06 JSON2WEB前端框架搭建 【J…...
Android 你遇到的无障碍onGesture不执行
你是不是和我一样,在开发无障碍应用的时候,翻边了Android的AccessibilityService源码 但是就是发现不了onGesture不执行的原因? 你是不是和我一样,在好多测试手机之间徘徊,发现还是不执行? 你是不是和我一…...

Java学习10
目录 一.多态: 1.方法的多态: 2.对象的多态: 3.多态的注意事项与细节: 5.多态的应用: 二.Java的动态绑定机制: 三.多态应用: 1.多态数组: 2.多态参数: 三.Object类…...

第二十章 TypeScript(webpack构建ts+vue3项目)
构建项目目录 src-- main.ts-- App.vue--shim.d.tswebpack.config.jsindex.htmlpackage.jsontsconfig.json 基础构建 npm install webpack -D npm install webpack-dev-server -D npm install webpack-cli -D package.json 添加打包命令和 启动服务的命令 {"scripts…...

白酒:陈酿过程中的老熟度评价与品质提升方法
在豪迈白酒的酿造过程中,陈酿是一个至关重要的环节。陈酿不仅能使白酒老熟,提品质,还能发展出与众不同的风味和口感。云仓酒庄深知陈酿的重要性,并进行了深入的研究和实践。本文将探讨陈酿过程中的老熟度评价与品质提升方法。 首先…...
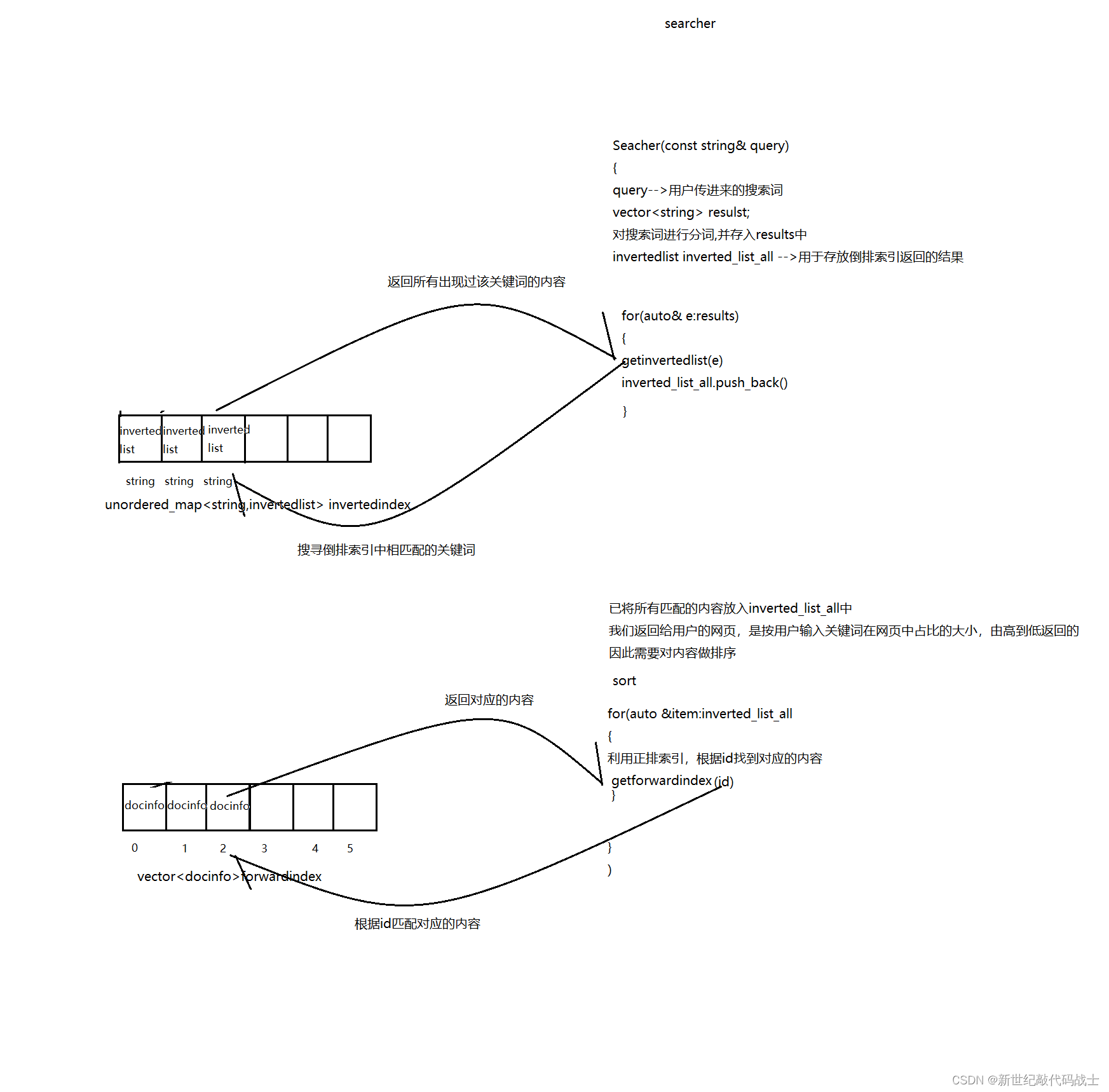
BoostSeacher
前言: 基于Boost库的搜索引擎 为何基于Boost库? 从技术上说:这个项目用了很多Boost库的接口从搜索引擎存储内说:存储的内容是Boost库的内容预期效果 预期效果:用户在浏览器输入关键词,浏览器显示相关结果 STEP1&#x…...
)
我的算法刷题笔记(3.18-3.22)
我的算法刷题笔记(3.18-3.22) 1. 螺旋矩阵1. total是总共走的步数2. int[][] directions {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};方位3. visited[row][column] true;用于判断是否走完一圈 2. 生命游戏1. 使用额外的状态22. 再复制一份数组 3. 旋转图像观…...

初探Ruby编程语言
文章目录 引言一、Ruby简史二、Ruby特性三、安装Ruby四、命令行执行Ruby五、Ruby的编程模型六、案例演示结语 引言 大家好,今天我们将一起探索一门历史悠久、充满魅力的编程语言——Ruby。Ruby是由松本行弘(Yukihiro Matsumoto)于1993年发明…...

深圳MES系统如何提高生产效率
深圳MES系统可以通过多种方式提高生产效率,具体如下: 实时监控和分析:MES系统可以实时收集并分析生产数据,帮助企业及时了解生产状况,发现问题并迅速解决,避免问题扩大化。这种实时监控和分析功能可以显著…...

QT常见Layout布局器使用
布局简介 为什么要布局?通过布局拖动不影响鼠标拖动窗口的效果等优点.QT设计器布局比较固定,不方便后期修改和维护;在Qt里面布局分为四个大类 : 盒子布局:QBoxLayout 网格布局:QGridLayout 表单布局&am…...
Elasticsearch8 - Docker安装Elasticsearch8.12.2
前言 最近在学习 ES,所以需要在服务器上装一个单节点的 ES 服务器环境:centos 7.9 安装 下载镜像 目前最新版本是 8.12.2 docker pull docker.elastic.co/elasticsearch/elasticsearch:8.12.2创建配置 新增配置文件 elasticsearch.yml http.host…...

还在为不知道怎么学习网络安全而烦恼吗?这篇文带你从入门级开始学习网络安全—认识网络安全
随着网络安全被列为国家安全战略的一部分,这个曾经细分的领域发展提速了不少,除了一些传统安全厂商以外,一些互联网大厂也都纷纷加码了在这一块的投入,随之而来的吸引了越来越多的新鲜血液不断涌入。 不同于Java、C/C等后端开发岗…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...
