【PyTorch】解决PyTorch安装中torch.cuda.is_available()返回False的问题
最近在安装PyTorch时遇到torch.cuda.is_available() = False的问题,特此记录下解决方法,以帮助其他遇到相同问题的人。
问题描述
Ubuntu 20.04,3060 Laptop,安装了CUDA 11.4,在Anaconda下新建了Python 3.8的环境,并且使用pytorch官网https://pytorch.org/get-started/previous-versions/,提供的如下安装指令
# CUDA 11.3
conda install pytorch==1.12.1 torchvision==0.13.1 torchaudio==0.12.1 cudatoolkit=11.3 -c pytorch
安装适合11.3的版本是因为CUDA 11.4版本似乎比较特殊,官网并未提供适用于11.4的pytorch,经网上查询得知可以兼容11.3的。
然而,在虚拟环境中import torch之后使用torch.cuda.is_available()检查CUDA是否可用时,返回False。尽管电脑有GPU(执行nvidia-smi能够打印GPU信息),但无法利用其加速功能,非常无语。
以下是检查的步骤:
1. 确认PyTorch安装方式:
首先,需要确认PyTorch是以CPU版本还是GPU版本安装的。在自己创建的虚拟环境中,运行conda list命令查看已安装的PyTorch版本。如果发现安装的是CPU版本,需要将其卸载并重新安装GPU版本。
注意一个非常坑的地方:
用conda install安装的pytorch都是CPU版本的!!!
应该用pip install来安装
2. 卸载并且重新安装PyTorch:
如果发现安装的是CPU版本,需要卸载并重新安装PyTorch。强烈建议使用PIP安装方式,而不是通过conda安装。
进入虚拟环境,使用conda remove命令卸载PyTorch及相关包。例如:
conda remove pytorch torchvision torchaudio cudatoolkit
这将会卸载当前环境中安装的PyTorch、torchvision、torchaudio和cudatoolkit等包。
我换了另外一个版本安装
pip install torch==1.11.0+cu113 torchvision==0.12.0+cu113 torchaudio==0.11.0 --extra-index-url https://download.pytorch.org/whl/cu113
3. 检查版本匹配性:
如果安装了GPU版本的PyTorch,但仍然遇到torch.cuda.is_available()返回False的问题,可能是版本不匹配导致的。请确保安装的PyTorch版本与CUDA版本相匹配,避免版本不一致导致的兼容性问题。
相关文章:
返回False的问题)
【PyTorch】解决PyTorch安装中torch.cuda.is_available()返回False的问题
最近在安装PyTorch时遇到torch.cuda.is_available() False的问题,特此记录下解决方法,以帮助其他遇到相同问题的人。 问题描述 Ubuntu 20.04,3060 Laptop,安装了CUDA 11.4,在Anaconda下新建了Python 3.8的环境&…...
95% 的公司面临 API 安全问题
API 对企业安全发挥着关键作用,但绝大多数企业都为此遭受日益严重的安全风险。据安全公司 Fastly最近做的一项调查显示,84% 的受访企业缺乏足够的API安全措施,95%的企业在过去1年中遇到过 API 安全问题。 此外,79%的受访企业出于A…...

mysql的基本知识点-排序和分组
分组(GROUP BY) GROUP BY 语句用于结合聚合函数,根据一个或多个列对结果集进行分组。例如,假设你有一个包含销售数据的表,并且你想按产品类别计算总销售额。你可以使用 GROUP BY 和 SUM() 函数来实现这一点。 SELECT…...
使用uniapp 的 plus.sqlite 操作本地数据库报错:::table xxx has no column named xxxx
背景: 1、使用uniapp 的 plus.sqlite 进行APP本地数据库操作 2、SQLite 模块用于操作本地数据库文件,可实现数据库文件的创建,执行SQL语句等功能。 遇到:在之前创建的表上进行新增字段的操作时候,出现问题:…...
)
第十五届蓝桥杯模拟赛 第三期 (C++)
第二次做蓝桥模拟赛的博客记录,可能有很多不足的地方,如果大佬有更好的思路或者本文中出现错误,欢迎分享思路或者提出意见 题目A 请问 2023 有多少个约数?即有多少个正整数,使得 2023 是这个正整数的整数倍。 答案&…...
Linux中的常用基础操作
ls 列出当前目录下的子目录和文件 ls -a 列出当前目录下的所有内容(包括以.开头的隐藏文件) ls [目录名] 列出指定目录下的子目录和文件 ls -l 或 ll 以列表的形式列出当前目录下子目录和文件的详细信息 pwd 显示当前所在目录的路径 ctrll 清屏 cd…...
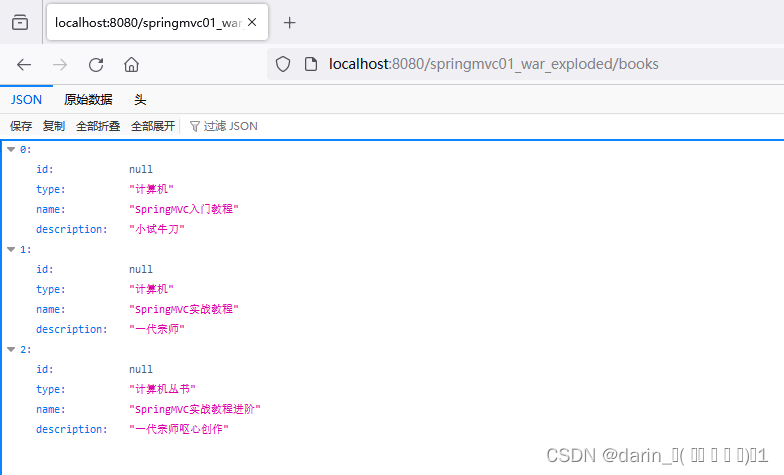
【SpringMVC】知识汇总
SpringMVC 短暂回来,有时间就会更新博客 文章目录 SpringMVC前言一、第一章 SpingMVC概述二、SpringMVC常用注解1. Controller注解2. RequestMapping注解3. ResponseBody注解4. RequestParam5. EnableWebMvc注解介绍6. RequestBody注解介绍7. RequestBody与RequestP…...

android13实现切换导航模式功能
支持android13以上系统,需要系统签名。 public class NavigationHelper {/*** 设置导航模式** param context* param mode GESTURAL:手势 TWOBUTTON:二按钮 THREEBUTTON:三按钮*/public static void setNavigationMode(Contex…...

Pycharm服务器配置python解释器并结合内网穿透实现公网远程开发
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…...

vue3+vite+Electron构建跨平台应用
1.搭建第一个 electron-vite 项目 electron-vite 是一个新型构建工具,旨在为 Electron 提供更快、更精简的开发体验。它主要由五部分组成: 一套构建指令,它使用 Vite 打包你的代码,并且它能够处理 Electron 的独特环境,包括 Node.js 和浏览器环境。 集中配置主进程、渲染…...
学习次模函数-第1章 引言
许多组合优化问题可以被转换为集合函数的最小化,集合函数是在给定基集合的子集的集合上定义的函数。同样地,它们可以被定义为超立方体的顶点上的函数,即,其中是基集合的基数-它们通常被称为伪布尔函数[27]。在这些集合函数中&…...

实在数字员工,助力菜鸟智慧物流高效腾飞,领航行业新高度
秉承人人都有一个智能助理的发展愿景,自2023年首个数字员工落地以来,菜鸟数字员工累计运行时长已达10万小时。 在智能物流科技不断飞速迭代的今天,物流行业作为社会经济运行的重要支柱和电子商务生态链的关键环节,面临着前所未…...

【from PIL import Image】PIL库和Image的功能及用法
from PIL import Image代码 from PIL import Image 是 Python 中导入 PIL 库中的 Image 模块。PIL 是 Python Imaging Library 的缩写,它是 Python 中用于图像处理的一个强大的库。而 Image 模块则是 PIL 库中的一个子模块,提供了处理图像的各种功能。 …...
【python从入门到精通】--第一战:安装python
🌈 个人主页:白子寰 🔥 分类专栏:python从入门到精通,魔法指针,进阶C,C语言,C语言题集,C语言实现游戏👈 希望得到您的订阅和支持~ 💡 坚持创作博文…...

MySQL的利用分区功能将数据存储到不同的磁盘
MySQL支持将不同的分区存储在不同的磁盘或目录上,这可以进一步优化I/O性能和存储利用率。具体的操作步骤如下: 首先需要确保MySQL的数据目录配置允许在不同目录存储数据文件。在MySQL配置文件(my.cnf或my.ini)中添加以下配置项: [mysqld] innodb_file_per_table1 这个配置项…...

KDB+Q | D1 | 学习资源 基础数据类型
官网会是主要的学习资源:https://code.kx.com/q/ 中文教程可能读起来会快一点: https://kdbcn.gitee.io/ 参考了还不错的学习经验帖:https://www.jianshu.com/p/488764d42627 KDB擅长处理时序数据, KDB数据库是后端数据库&…...
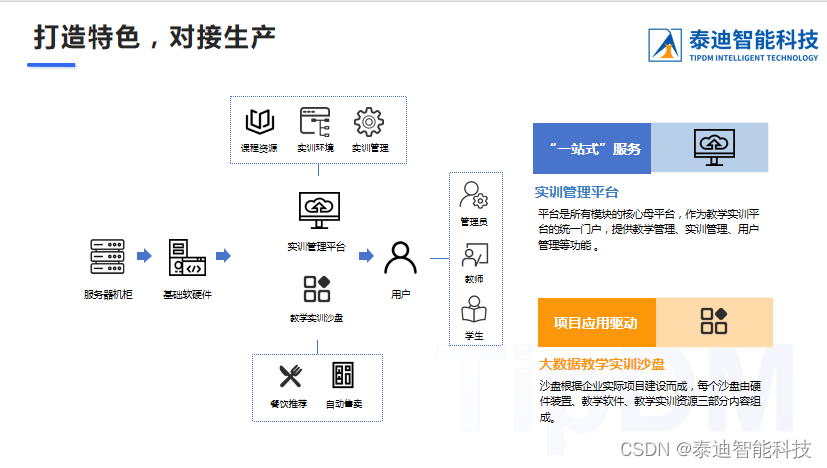
中等职业学校大数据课程建设方案
大数据产业是以数据及数据所蕴含的信息价值为核心生产要素,通过数据技术、数据产品、数据服务等形式,使数据与信息价值在各行业经济活动中得到充分释放的赋能型产业。 大数据产业定义一般分为核心业态、关联业态、衍生业态三大业态。 一、专…...

.NET 依赖注入和配置系统
文章目录 依赖注入DI几个概念.NET 中使用DI生命周期IServiceProvider的服务定位器方法 配置系统Json文件配置绑定类读取配置 依赖注入 依赖注入(Dependency Injection,DI)是控制反转(Inversion of Control,IOC…...

什么是”法兰“?
“法兰”,第一次听说这个词,怪怪的,后来就知道了和“鲁棒”是一类人才发明的词; 所以就知道这个词原本是“flange”; 那这样就好解释了, 【 使物体更加坚固或(如火车车轮)保持正确…...
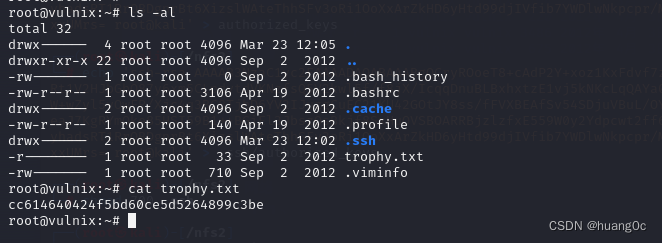
Vulnhub靶机:HackLAB_Vulnix
一、介绍 运行环境:Virtualbox(攻击机)和VMware(靶机) 攻击机:kali(192.168.56.101) 靶机:HackLAB: Vulnix(192.168.56.110) 目标:获取靶机root权限和flag 靶机下载地址&#x…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...
