当前位置： 首页 > news >正文

Excel 打开后提示：MicrosoftExcel无法计算某个公式。在打开的工作簿中有一个循环引用...

news 2026/2/11 1:19:55

目录预览

  • 一、问题描述
  • 二、原因分析
  • 三、解决方案
  • 四、参考链接

一、问题描述

MicrosoftExcel无法计算某个公式。在打开的工作簿中有一个循环引用，但无法列出导致循环的引I用。请尝试编辑上次输入的公式，或利用“撤消”命令删除该公式，如下图：

在这里插入图片描述

解释：
循环引用是指在Excel中的公式中使用了相互引用的单元格，导致计算无法结束或陷入无限循环。这可能是因为您在公式中引用了当前单元格，或者多个单元格之间的相互引用。

二、原因分析

按照提示：说是公式有问题，那就显示公式去掉公式试试呗
步骤：公式-公式审核-显示公式

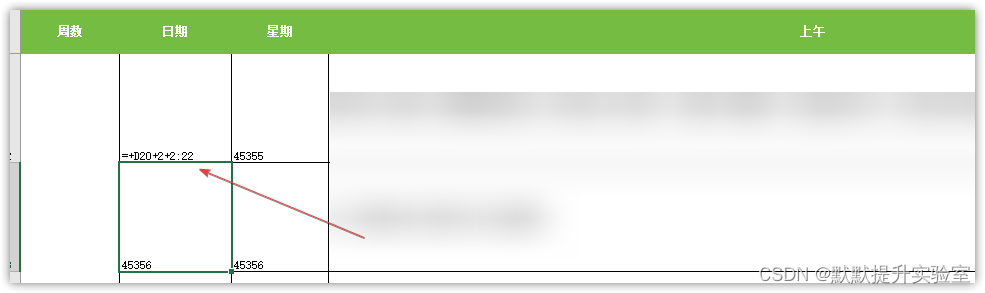
在这里插入图片描述
在这里插入图片描述

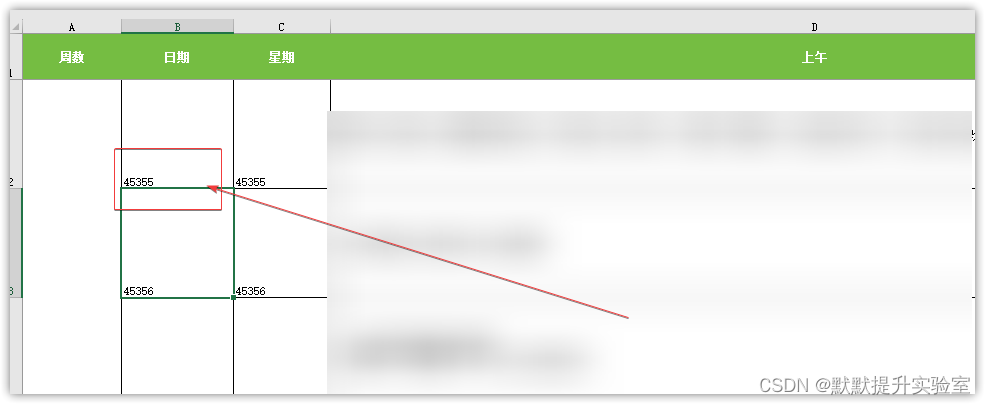
还可以直接看底部提示哪个单元格有问题：

在这里插入图片描述
然后直接定位到有问题的单元格进行修改即可。

三、解决方案

解决此问题的方法是检查公式并删除循环引用，或者通过更改公式来避免循环引用。

  • 删除公式，然后格式刷刷一下就好了。

在这里插入图片描述

四、参考链接

Excel打开后总提示循环引用怎么办？

如能帮你解决问题，请点赞收藏评论，帮助更多的人解决问题。

相关文章：

Excel 打开后提示：MicrosoftExcel无法计算某个公式。在打开的工作簿中有一个循环引用...

目录预览 一、问题描述二、原因分析三、解决方案四、参考链接 一、问题描述 MicrosoftExcel无法计算某个公式。在打开的工作簿中有一个循环引用，但无法列出导致循环的引I用。请尝试编辑上次输入的公式，或利用“撤消”命令删除该公式，如下图&…...

编程日记 2024/3/26 3:14:36

【自我提升】计算机领域相关证书

目录 计算机技术与软件专业资格（水平）考试证书（软考）Oracle认证Cisco认证微软认证红帽认证AWS认证 计算机技术与软件专业资格（水平）考试证书（软考） 计算机技术与软件专业技术资格&a…...

编程日记 2024/3/26 3:13:35

外包干了15天，技术退步明显。。。。。

先说一下自己的情况，本科生，2019年我通过校招踏入了南京一家软件公司，开始了我的职业生涯。那时的我，满怀热血和憧憬，期待着在这个行业中闯出一片天地。然而，随着时间的推移，我发现自己逐渐陷入…...

编程日记 2024/3/26 3:10:33

人工智能（Educoder）-- 搜索技术 -- 启发式搜索

任务描述 本关任务：八数码问题是在一个33的棋盘上有1−8位数字随机分布，以及一个空格，与空格相连的棋子可以滑动到空格中，问题的解是通过空格滑动，使得棋盘转化为目标状态，如下图所示。 为了简化问题的输…...

编程日记 2024/3/26 3:09:32

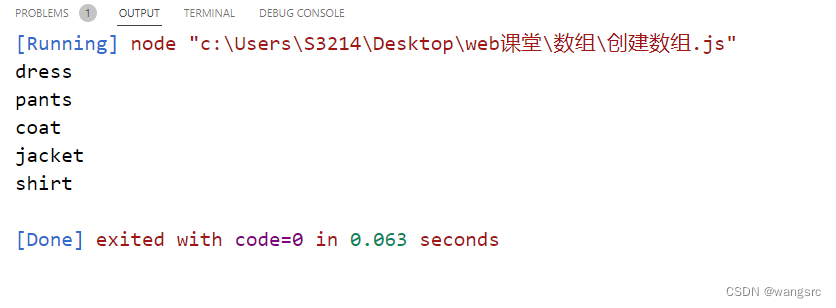
计算平均分 javascript

养成好习惯&#xff1a;先写注释再写代码 基础版&#xff1a;直接写逻辑&#xff08;平均分总和/个数&#xff09; // 求平均分 var scores [60, 55, 80, 33, 75, 100]; // 求和,相除 var sum 0; var avg;for (var i 0; i < 6; i) {sum scores[i]; }avg sum / 6; con…...

编程日记 2024/3/26 3:07:30

Redis入门到实战-第三弹

Redis入门到实战 Redis数据类型官网地址Redis概述Redis数据类型介绍更新计划 Redis数据类型 官网地址 声明: 由于操作系统, 版本更新等原因, 文章所列内容不一定100%复现, 还要以官方信息为准 https://redis.io/Redis概述 Redis是一个开源的&#xff08;采用BSD许可证&#…...

编程日记 2024/3/26 3:03:26

AnyGo for Mac最新激活版：位置模拟软件打破地域限制

AnyGo for Mac&#xff0c;一款专为Mac用户打造的位置模拟软件&#xff0c;让您能够轻松打破地域限制&#xff0c;畅享无限可能。 软件下载&#xff1a;AnyGo for Mac v7.0.0最新激活版 通过AnyGo&#xff0c;您可以随时随地模拟出任何地理位置&#xff0c;无论是国内热门景点还…...

编程日记 2024/3/26 2:58:21

【Mysql数据库基础07】DDL 数据定义语言

Data Definition Language 1 库的操作1.1 create 创建1.2 alter 修改1.3 drop 删除 2 表的操作2.1 表的创建2.2 表的修改2.2.1 修改表名2.2.2 修改列名2.2.3 修改列的类型和约束2.2.4 添加列2.2.5 删除列 2.3 表的删除2.4 表的复制 3 练习 1 库的操作 1.1 create 创建 create…...

编程日记 2024/3/26 2:57:19

数据库及中表的创建和管理

目录 创建数据库 使用数据库（使用，查看信息） 修改数据库(删除，修改)...

编程日记 2024/3/26 2:56:17

git笔记之撤销、回退、reset方面的笔记

git笔记之撤销、回退、reset方面的笔记 code review! 文章目录 git笔记之撤销、回退、reset方面的笔记1.git 已经commit了&#xff0c;还没push&#xff0c;如何撤销到初始状态git reset --soft HEAD~1git reset HEAD~1&#xff08;等同于 git reset --mixed HEAD~1&#xff0…...

编程日记 2024/3/26 2:53:15

【中间件】docker数据卷

&#x1f4dd;个人主页&#xff1a;五敷有你 &#x1f525;系列专栏&#xff1a;中间件 ⛺️稳中求进&#xff0c;晒太阳 1.数据卷&#xff08;容器数据管理&#xff09; 修改nginx的html页面时&#xff0c;需要进入nginx内部。并且因为内部没有编辑器&#xff0c;修改…...

编程日记 2024/3/26 2:52:14

【3D reconstruction 学习笔记 第二部】

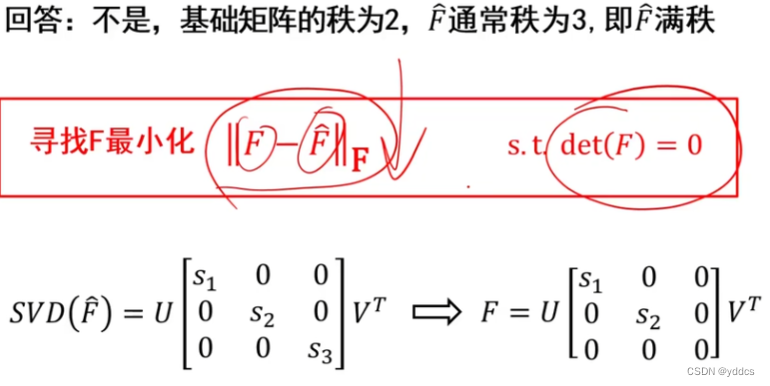
三维重建 3D reconstruction 4. 三维重建与极几何三角化&#xff08;线性解法&#xff09;三角化&#xff08;非线性解法&#xff09;多视图几何极几何极几何约束基础矩阵估计 5. 双目立体视觉重建6. 多视图重建7. SFM 系统设计8. SLAM系统设计 4. 三维重建与极几何 三角化&…...

编程日记 2024/3/26 2:51:12

【CSP试题回顾】202109-1-数组推导（优化）

CSP-202109-1-数组推导 解题代码 #include <iostream> #include <vector> #include <algorithm> using namespace std;long long n, sumMax,sumMin;int main() {cin >> n;vector<long long>arr(n);for (size_t i 0; i < n; i){cin >>…...

编程日记 2024/3/26 2:48:10

Redis - 高并发场景下的Redis最佳实践_翻过6座大山

文章目录 概述6座大山之_缓存雪崩 &#xff08;缓存全部失效&#xff09;缓存雪崩的两种常见场景如何应对缓存雪崩&#xff1f; 6座大山之_缓存穿透&#xff08;查询不存在的 key&#xff09;缓存穿透的原因解决方案1. 数据校验2. 缓存空值3. 频控4. 使用布隆过滤器 6座大山之_…...

编程日记 2024/3/26 2:46:08

数字乡村发展策略：科技引领农村实现跨越式发展

随着信息技术的迅猛发展和数字经济的崛起&#xff0c;数字乡村发展策略已经成为引领农村实现跨越式发展的重要手段。科技的力量正在深刻改变着传统农业的生产方式、农村的社会结构以及农民的生活方式&#xff0c;为农村经济发展注入了新的活力和动力。本文将从数字乡村的内涵、…...

编程日记 2024/3/26 2:43:05

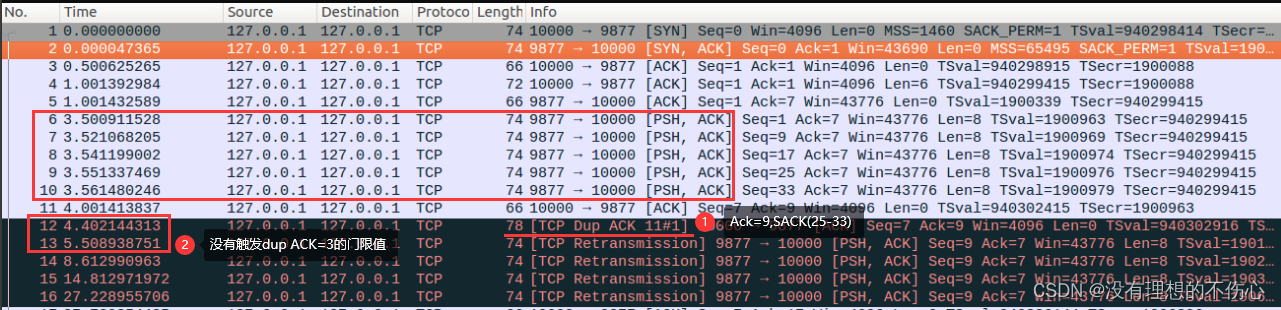
TCP重传机制详解——04FACK

文章目录 TCP重传机制详解——04FACK什么是FACKFACK的发展为什么要引入FACK实战抓包讲解开启FACK场景&#xff0c;且达到dup ACK门限值开启FACK场景&#xff0c;未达到dup ACK门限值 为什么要淘汰FACK总结REF TCP重传机制详解——04FACK 什么是FACK FACK的全称是forward ackn…...

编程日记 2024/3/26 2:42:04

安卓Java面试题 206- 210

206. 简述如何统计Activity的工作时间 ？如何统计Activity启动所用的时间？ 可以通过分析Log得到（这个就是DDMS的那个Log）。 当我们点击触摸时会了类似以下的Log A： 03-06 03:36:47.865: VERBOSE/InputDevice(2486): ID[0]=0(0) Dn (0=>1) 03-06 03:36:47.865: INFO/Powe…...

编程日记 2024/3/26 2:37:00

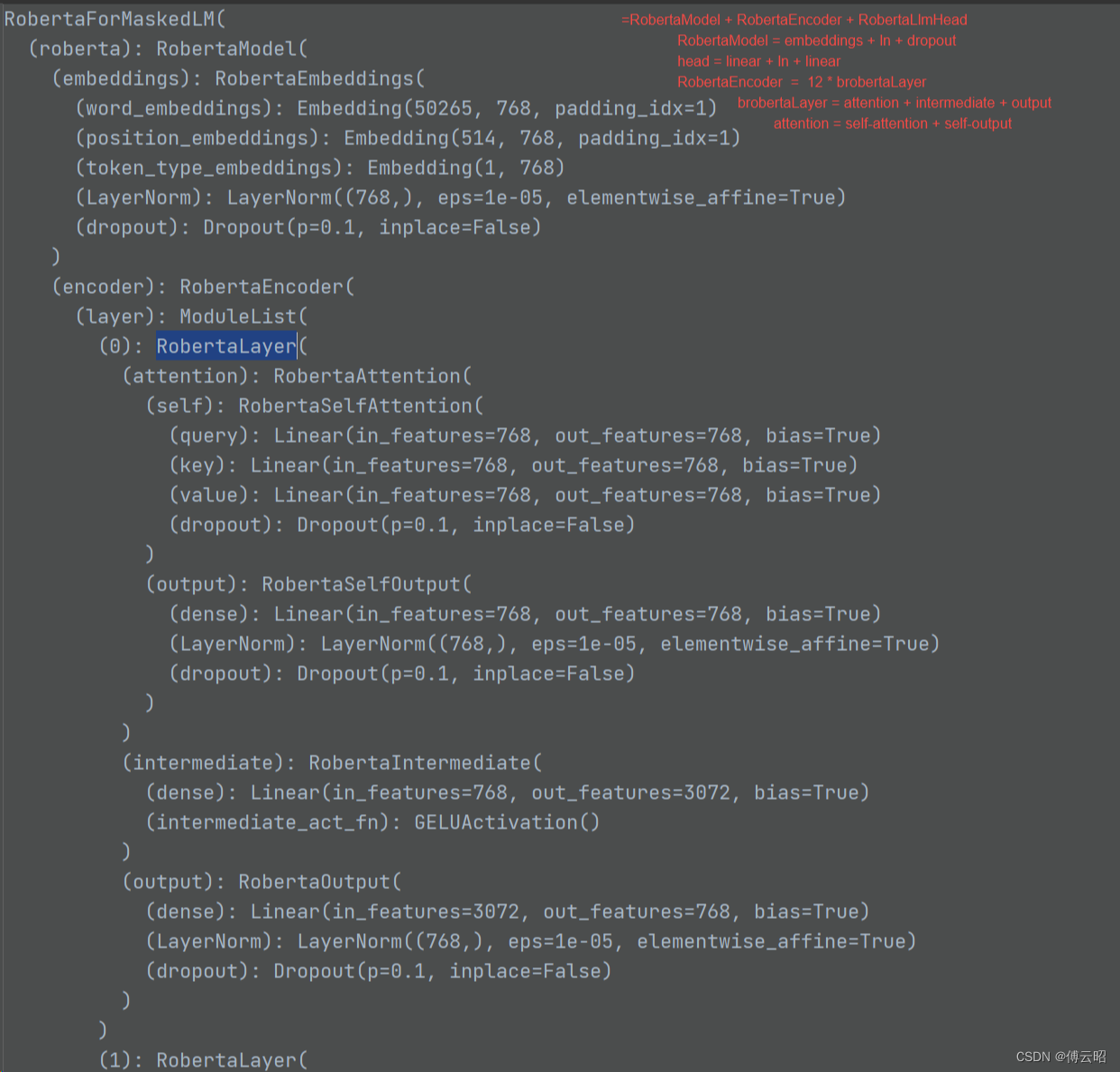
huggingface的transformers训练bert

目录 理论 实践 理论 https://arxiv.org/abs/1810.04805 BERT&#xff08;Bidirectional Encoder Representations from Transformers&#xff09;是一种自然语言处理&#xff08;NLP&#xff09;模型&#xff0c;由Google在2018年提出。它是基于Transformer模型的预训练方法…...

编程日记 2024/3/26 2:35:59

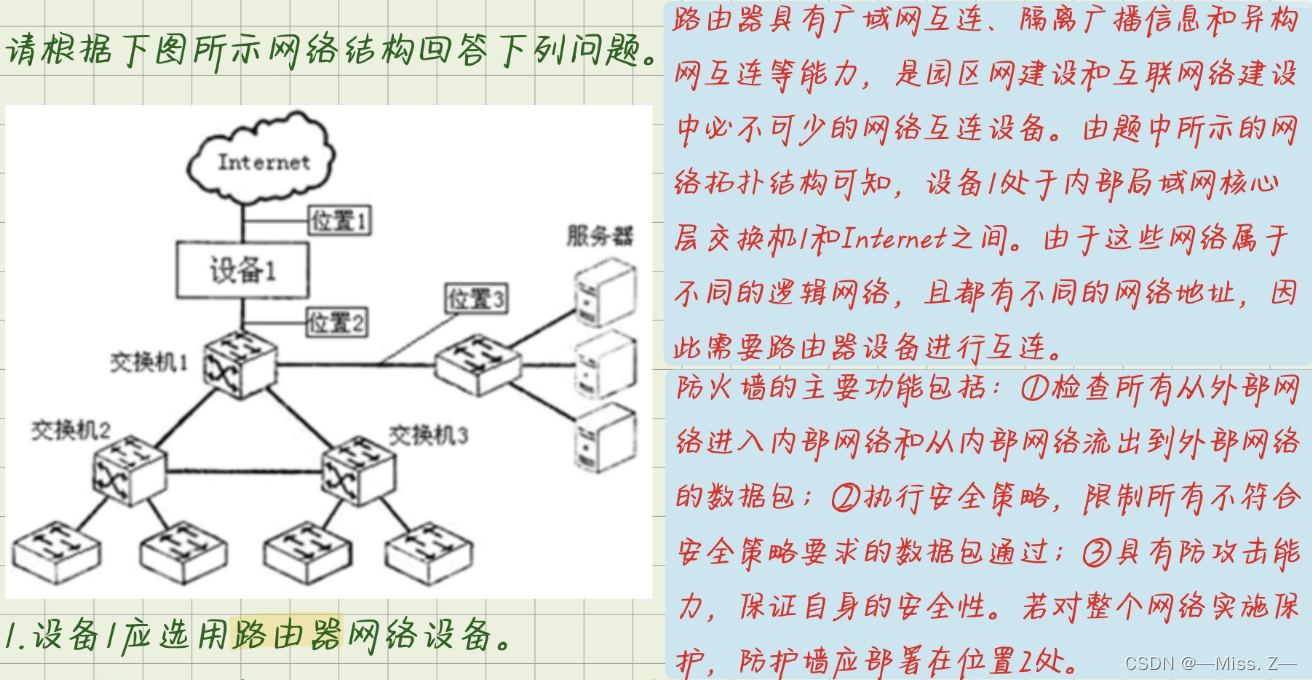
计算机三级——网络技术（综合题第五题）

第一题 填写路由器RG的路由表项①至④。 目的网络&#xff0f;掩码长度输出端口输出端口172.19.63.192&#xff0f;30S0(直接连接)172.19.63.188&#xff0f;30S1(直接连接) 路由器RG的S0的IP地址是172.19.63.193&#xff0c;路由器RE的S0的IP地址是172.19.63.194。 【解析】…...

编程日记 2024/3/26 2:33:57

C#使用ASP.NET Core Razor Pages构建网站（三）

上一篇文章了解Razor Pages 链接&#xff1a;C#使用ASP.NET Core Razor Pages构建网站&#xff08;二&#xff09; 接下来继续了解ASP.NET Core Razor Pages构建网站的后续内容 一、将Entity Framework Core配置为服务 要在 ASP.NET Core 项目中配置 Entity Framework Core 服…...

编程日记 2024/3/26 2:30:55

React 第五十五节 Router 中 useAsyncError的使用详解

前言 useAsyncError 是 React Router v6.4 引入的一个钩子&#xff0c;用于处理异步操作&#xff08;如数据加载&#xff09;中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误&#xff1a;捕获在 loader 或 action 中发生的异步错误替…...

编程新知 2025/11/25 10:36:53

Java 语言特性(面试系列2)

一、SQL 基础 1. 复杂查询 &#xff08;1&#xff09;连接查询&#xff08;JOIN&#xff09; 内连接&#xff08;INNER JOIN&#xff09;&#xff1a;返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

编程新知 2025/10/24 14:20:29

C++实现分布式网络通信框架RPC(3)--rpc调用端

目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中&#xff0c;我们已经大致实现了rpc服务端的各项功能代…...

编程新知 2026/2/8 20:42:58

模型参数、模型存储精度、参数与显存

模型参数量衡量单位 M&#xff1a;百万&#xff08;Million&#xff09; B&#xff1a;十亿&#xff08;Billion&#xff09; 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的&#xff0c;但是一个参数所表示多少字节不一定&#xff0c;需要看这个参数以什么…...

编程新知 2025/12/20 12:32:08

MongoDB学习和应用(高效的非关系型数据库)

一丶 MongoDB简介 对于社交类软件的功能&#xff0c;我们需要对它的功能特点进行分析&#xff1a; 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具&#xff1a; mysql&#xff1a;关系型数据库&am…...

编程新知 2026/1/23 10:24:30

通过Wrangler CLI在worker中创建数据库和表

官方使用文档&#xff1a;Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后&#xff0c;会在本地和远程创建数据库&#xff1a; npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库&#xff1a; 现在&#xff0c;您的Cloudfla…...

编程新知 2026/1/31 6:18:08

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别

UnsatisfiedLinkError 在对接硬件设备中&#xff0c;我们会遇到使用 java 调用 dll文件 的情况&#xff0c;此时大概率出现UnsatisfiedLinkError链接错误&#xff0c;原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用&#xff0c;结果 dll 未实现 JNI 协…...

编程新知 2025/10/6 16:38:04

Qwen3-Embedding-0.6B深度解析：多语言语义检索的轻量级利器

第一章 引言&#xff1a;语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域&#xff0c;文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量&#xff0c;支撑着搜索引擎、推荐系统、…...

编程新知 2025/11/6 8:47:31

Spring数据访问模块设计

前面我们已经完成了IoC和web模块的设计&#xff0c;聪明的码友立马就知道了&#xff0c;该到数据访问模块了&#xff0c;要不就这俩玩个6啊&#xff0c;查库势在必行&#xff0c;至此&#xff0c;它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据&#xff08;数据库、No…...

编程新知 2026/2/4 16:13:50

安卓基础（aar）

重新设置java21的环境&#xff0c;临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的&#xff1a; MyApp/ ├── app/ …...

编程新知 2026/1/25 8:10:56