【算法篇】逐步理解动态规划1(斐波那契数列模型)
目录
斐波那契数列模型
1. 第N个泰波那契数
2.使用最小花费爬楼梯
3.解码方法
学过算法的应该知道,动态规划一直都是一个非常难的模块,无论是状态转移方程的定义还是dp表的填表,都非常难找到思路。在这个算法的支线专题中我会结合很多力扣题型,由简单到复杂,带大家深度剖析动态规划类的题型,欢迎大家关注啊。
顺序:
题目链接-》算法思路-》代码呈现
斐波那契数列模型
动态规划类题目解题步骤:
- 依据题目进行状态表示(dp[i]的含义)
- 写出状态转移方程(类似于dp[i]=dp[i-1]+dp[i-2])
- 为防止填表时数组越界,对dp表进行初始化(dp[0]=dp[1]=1)
- 搞清楚填表顺序(从前往后或者从后往前)
- 利用dp表返回问题答案
1. 第N个泰波那契数
题目链接:
https://leetcode.cn/problems/n-th-tribonacci-number/description/

算法思路:
代码呈现:
class Solution {public int tribonacci(int n) {if(n==0){return 0;}if(n==1||n==2){return 1;}int[] dp=new int[n+1];dp[0]=0;dp[1]=1;dp[2]=1;for(int i=3;i<=n;i++){dp[i]=dp[i-1]+dp[i-2]+dp[i-3];}return dp[n];}
}2.使用最小花费爬楼梯
题目链接:
https://leetcode.cn/problems/min-cost-climbing-stairs/description/

算法思路:
- 先到达 i - 1 的位置,然后⽀付 cost[i - 1] ,接下来⾛⼀步⾛到 i 位置: dp[i - 1] + csot[i - 1] ;
- 先到达 i - 2 的位置,然后⽀付 cost[i - 2] ,接下来⾛⼀步⾛到 i 位置: dp[i - 2] + csot[i - 2] 。
代码呈现:
class Solution {public int minCostClimbingStairs(int[] cost) {int size=cost.length;if(size==2) return Math.min(cost[0],cost[1]);int[] dp=new int[size+1];dp[0]=0;dp[1]=0;dp[2]=Math.min(cost[0],cost[1]);for(int i=3;i<=size;i++){dp[i]=Math.min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);}return dp[size];}
}3.解码方法
题目链接:
https://leetcode.cn/problems/decode-ways/
算法思路:
- 让 i 位置上的数与 i - 1 位置上的数结合在⼀起,解码成⼀个字⺟,也存在「解码成功」和「解码失败」两种情况:
i. 解码成功:当结合的数在 [10, 26] 之间的时候,说明 [i - 1, i] 两个位置是可以解码成功的,那么此时 [0, i] 区间上的解码⽅法应该等于 [0, i - 2 ] 区间上的解码⽅法,原因同上。此时 dp[i] = dp[i - 2] ;
ii. 解码失败:当结合的数在 [0, 9] 和 [27 , 99] 之间的时候,说明两个位置结合后解码失败(这⾥⼀定要注意 00 01 02 03 04 ...... 这⼏种情况),那么此时 [0, i] 区间上的解码⽅法就不存在了,原因依旧同上。此时 dp[i] = 0 。
- 让 i 位置上的数单独解码成⼀个字⺟,就存在「解码成功」和「解码失败」两种情况:
i. 解码成功:当 i 位置上的数在 [1, 9] 之间的时候,说明 i 位置上的数是可以单独解 码的,那么此时 [0, i] 区间上的解码⽅法应该等于 [0, i - 1] 区间上的解码⽅ 法。因为 [0, i - 1] 区间上的所有解码结果,后⾯填上⼀个 i 位置解码后的字⺟就 可以了。此时 dp[i] = dp[i - 1] ;
ii. 解码失败:当 i 位置上的数是 0 的时候,说明 i 位置上的数是不能单独解码的,那么此时 [0, i] 区间上不存在解码⽅法。因为 i 位置如果单独参与解码,但是解码失败了,那么前⾯做的努⼒就全部⽩费了。此时 dp[i] = 0 。
代码呈现:
class Solution {public int numDecodings(String s) {char[] arr=s.toCharArray();int n=arr.length;int[] dp=new int[n+1];dp[0]=1;if(arr[0]=='0') dp[1]=0;else dp[1]=1;if(n==1){return dp[1];}for(int i=2;i<n+1;i++){if(arr[i-1]!='0'){dp[i]+=dp[i-1];}if(((arr[i-2]-'0')*10+(arr[i-1]-'0'))<=26&&((arr[i-2]-'0')*10+(arr[i-1]-'0'))>=10){dp[i]+=dp[i-2];}}return dp[n];}
}相关文章:

【算法篇】逐步理解动态规划1(斐波那契数列模型)
目录 斐波那契数列模型 1. 第N个泰波那契数 2.使用最小花费爬楼梯 3.解码方法 学过算法的应该知道,动态规划一直都是一个非常难的模块,无论是状态转移方程的定义还是dp表的填表,都非常难找到思路。在这个算法的支线专题中我会结合很多力…...

软件测试 - postman高级使用
断言 概念:让程序代替人判断测试用例执行的结果是否符合预期的一个过程 特点: postman断言使用js编写,断言写在postman的tests中 tests脚本在发送请求之后执行,会把断言的结果最终在testresult中进行展示 常用的postman提供的…...
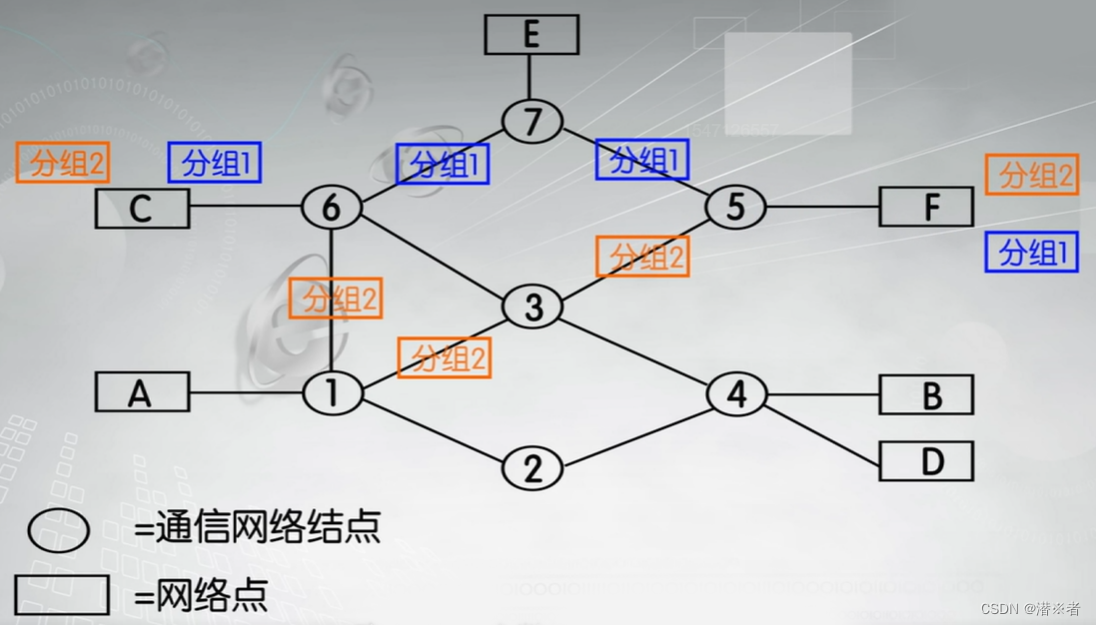
数据交换技术
目录 <线路交换> <报文交换> <分组交换> 1.数据报分组交换 2.虚电路分组交换 计算机网络是以数据交换为目的的技术,从交换技术的发展过程来看,主要经历了线 路交换、报文交换、分组交换的过程。 <线路交换> 线路交换又称为…...
)
FFmpeg-- mp4文件合成1:aac和h264封装(c++实现)
文章目录 流程api核心代码muxer.hmuxer.cppaac 和 h264 封装为视频流,封装为c++的Muxter类 流程 分配视频文件上下文 int Init(const char *url); 创建流,赋值给视频的音频流和视频流 int AddStream(AVCodecContext *codec_ctx); 写视频流的head int SendHeader(); 写视频流的…...

【嵌入式开发 Linux 常用命令系列 1.3 -- 统计目录下有多少个文件】
统计目录下有多少个文件 在 Linux 中,你可以使用 find 命令和 wc(word count)命令的组合来统计当前目录及其子目录下的文件数量。如果你只对当前目录(不包括子目录)中的文件数量感兴趣,可以使用 ls 和 wc …...

JMeter 如何并发执行 Python 脚本
要在JMeter中并发执行Python脚本,可以使用Jython脚本或通过调用外部Python脚本的方式实现。 使用Jython脚本并发执行Python脚本的步骤: 1、创建一个线程组:在JMeter界面中,右键点击测试计划,选择 “添加” -> “线…...

第十三届蓝桥杯省赛真题 Java B 组【原卷】
文章目录 发现宝藏【考生须知】试题 A: 星期计算试题 B: 山试题 C: 字符统计试题 D: 最少刷题数试题 E \mathrm{E} E : 求阶乘试题 F : \mathrm{F}: F: 最大子矩阵试题 G: 数组切分试题 H: 回忆迷宫试题 I: 红绿灯试题 J 拉箱子 发现宝藏 前些天发现了一个巨牛的人工智能学习…...
Excel 打开后提示:MicrosoftExcel无法计算某个公式。在打开的工作簿中有一个循环引用...
目录预览 一、问题描述二、原因分析三、解决方案四、参考链接 一、问题描述 MicrosoftExcel无法计算某个公式。在打开的工作簿中有一个循环引用,但无法列出导致循环的引I用。请尝试编辑上次输入的公式,或利用“撤消”命令删除该公式,如下图&…...
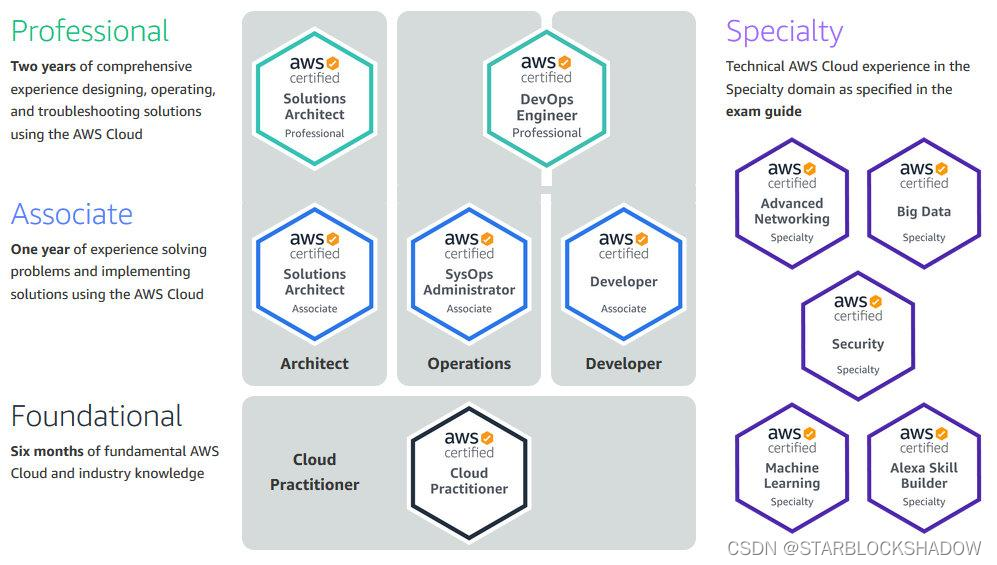
【自我提升】计算机领域相关证书
目录 计算机技术与软件专业资格(水平)考试证书(软考)Oracle认证Cisco认证微软认证红帽认证AWS认证 计算机技术与软件专业资格(水平)考试证书(软考) 计算机技术与软件专业技术资格&a…...
外包干了15天,技术退步明显。。。。。
先说一下自己的情况,本科生,2019年我通过校招踏入了南京一家软件公司,开始了我的职业生涯。那时的我,满怀热血和憧憬,期待着在这个行业中闯出一片天地。然而,随着时间的推移,我发现自己逐渐陷入…...

人工智能(Educoder)-- 搜索技术 -- 启发式搜索
任务描述 本关任务:八数码问题是在一个33的棋盘上有1−8位数字随机分布,以及一个空格,与空格相连的棋子可以滑动到空格中,问题的解是通过空格滑动,使得棋盘转化为目标状态,如下图所示。 为了简化问题的输…...
计算平均分 javascript
养成好习惯:先写注释再写代码 基础版:直接写逻辑(平均分总和/个数) // 求平均分 var scores [60, 55, 80, 33, 75, 100]; // 求和,相除 var sum 0; var avg;for (var i 0; i < 6; i) {sum scores[i]; }avg sum / 6; con…...
Redis入门到实战-第三弹
Redis入门到实战 Redis数据类型官网地址Redis概述Redis数据类型介绍更新计划 Redis数据类型 官网地址 声明: 由于操作系统, 版本更新等原因, 文章所列内容不一定100%复现, 还要以官方信息为准 https://redis.io/Redis概述 Redis是一个开源的(采用BSD许可证&#…...
AnyGo for Mac最新激活版:位置模拟软件打破地域限制
AnyGo for Mac,一款专为Mac用户打造的位置模拟软件,让您能够轻松打破地域限制,畅享无限可能。 软件下载:AnyGo for Mac v7.0.0最新激活版 通过AnyGo,您可以随时随地模拟出任何地理位置,无论是国内热门景点还…...

【Mysql数据库基础07】DDL 数据定义语言
Data Definition Language 1 库的操作1.1 create 创建1.2 alter 修改1.3 drop 删除 2 表的操作2.1 表的创建2.2 表的修改2.2.1 修改表名2.2.2 修改列名2.2.3 修改列的类型和约束2.2.4 添加列2.2.5 删除列 2.3 表的删除2.4 表的复制 3 练习 1 库的操作 1.1 create 创建 create…...

数据库及中表的创建和管理
目录 创建数据库 使用数据库(使用,查看信息) 修改数据库(删除,修改)...

git笔记之撤销、回退、reset方面的笔记
git笔记之撤销、回退、reset方面的笔记 code review! 文章目录 git笔记之撤销、回退、reset方面的笔记1.git 已经commit了,还没push,如何撤销到初始状态git reset --soft HEAD~1git reset HEAD~1(等同于 git reset --mixed HEAD~1࿰…...

【中间件】docker数据卷
📝个人主页:五敷有你 🔥系列专栏:中间件 ⛺️稳中求进,晒太阳 1.数据卷(容器数据管理) 修改nginx的html页面时,需要进入nginx内部。并且因为内部没有编辑器,修改…...
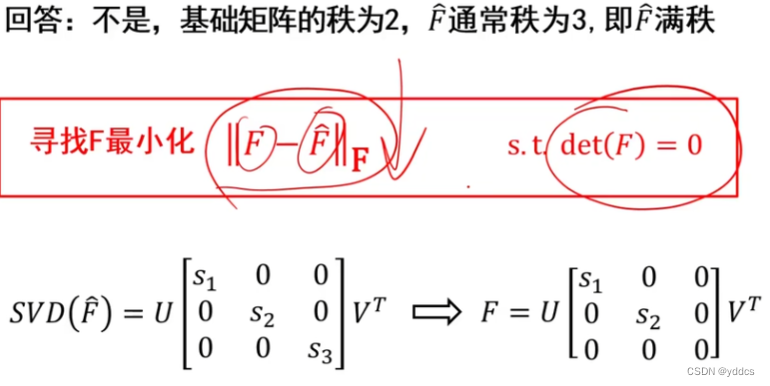
【3D reconstruction 学习笔记 第二部】
三维重建 3D reconstruction 4. 三维重建与极几何三角化(线性解法)三角化(非线性解法)多视图几何极几何极几何约束基础矩阵估计 5. 双目立体视觉重建6. 多视图重建7. SFM 系统设计8. SLAM系统设计 4. 三维重建与极几何 三角化&…...
)
【CSP试题回顾】202109-1-数组推导(优化)
CSP-202109-1-数组推导 解题代码 #include <iostream> #include <vector> #include <algorithm> using namespace std;long long n, sumMax,sumMin;int main() {cin >> n;vector<long long>arr(n);for (size_t i 0; i < n; i){cin >>…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...
