第十三届蓝桥杯省赛真题 Java B 组【原卷】
文章目录
- 发现宝藏
- 【考生须知】
- 试题 A: 星期计算
- 试题 B: 山
- 试题 C: 字符统计
- 试题 D: 最少刷题数
- 试题 E \mathrm{E} E : 求阶乘
- 试题 F : \mathrm{F}: F: 最大子矩阵
- 试题 G: 数组切分
- 试题 H: 回忆迷宫
- 试题 I: 红绿灯
- 试题 J 拉箱子
发现宝藏
前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。【宝藏入口】。
【考生须知】
考试开始后, 选手首先下载题目, 并使用考场现场公布的解压密码解压试题。
考试时间为 4 小时。考试期间选手可浏览自己已经提交的答案, 被浏览的答案允许拷贝。时间截止后,将无法继续提交或浏览答案。
对同一题目, 选手可多次提交答案, 以最后一次提交的答案为准。
选手必须通过浏览器方式提交自己的答案。选手在其它位置的作答或其它方式提交的答案无效。
试题包含 “结果填空” 和 “程序设计” 两种题型。
结果填空题: 要求选手根据题目描述直接填写结果。求解方式不限。不要求源代码。把结果填空的答案直接通过网页提交即可, 不要书写多余的内容。
程序设计题: 要求选手设计的程序对于给定的输入能给出正确的输出结果。考生的程序只有能运行出正确结果才有机会得分。
注意: 在评卷时使用的输入数据与试卷中给出的示例数据可能是不同的。选手的程序必须是通用的, 不能只对试卷中给定的数据有效。
所有源码必须在同一文件中。调试通过后,拷贝提交。
注意: 不要使用 package 语句。
注意:选手代码的主类名必须为: Main, 否则会被判为无效代码。
注意: 如果程序中引用了类库, 在提交时必须将 import 语句与程序的其他部分同时提交。只允许使用 Java 自带的类库。
试题 A: 星期计算
本题总分: 5 分
【问题描述】
已知今天是星期六, 请问 2 0 22 20^{22} 2022 天的后是星期几?
注意用数字 1 到 7 表示星期一到星期日。
【答案提交】
这是一道结果填空的题, 你只需要算出结果后提交即可。本题的结果为一个整数, 在提交答案时只填写这个整数, 填写多余的内容将无法得分。
试题 B: 山
本题总分: 5 分
【问题描述】
这天小明正在学数数。
他突然发现有些正整数的形状像一座 “山”, 比如 123565321、145541, 它们左右对称 (回文) 且数位上的数字先单调不减, 后单调不增。
小明数了很久也没有数完, 他想让你告诉他在区间 [ 2022 , 2022222022 ] [2022,2022222022] [2022,2022222022] 中有多少个数的形状像一座 “山”。
【答案提交】
这是一道结果填空的题, 你只需要算出结果后提交即可。本题的结果为一个整数, 在提交答案时只填写这个整数, 填写多余的内容将无法得分。
试题 C: 字符统计
时间限制: 1.0 s 1.0 \mathrm{~s} 1.0 s 内存限制: 512.0 M B 512.0 \mathrm{MB} 512.0MB 本题总分: 10 分
【问题描述】
给定一个只包含大写字母的字符串 S S S, 请你输出其中出现次数最多的字母。如果有多个字母均出现了最多次, 按字母表顺序依次输出所有这些字母。
【输入格式】
一个只包含大写字母的字符串 S S S.
【输出格式】
若干个大写字母, 代表答案。
【样例输入】
BABBACAC
【样例输出】
A B \mathrm{AB} AB
【评测用例规模与约定】
对于 100 % 100 \% 100% 的评测用例, 1 ≤ ∣ S ∣ ≤ 1 0 6 1 \leq|S| \leq 10^{6} 1≤∣S∣≤106.
试题 D: 最少刷题数
时间限制: 1.0 s 1.0 \mathrm{~s} 1.0 s 内存限制: 512.0 M B 512.0 \mathrm{MB} 512.0MB 本题总分: 10 分
【问题描述】
小蓝老师教的编程课有 N N N 名学生, 编号依次是 1 … N 1 \ldots N 1…N 。第 i i i 号学生这学期刷题的数量是 A i A_{i} Ai 。
对于每一名学生, 请你计算他至少还要再刷多少道题, 才能使得全班刷题比他多的学生数不超过刷题比他少的学生数。
【输入格式】
第一行包含一个正整数 N N N 。
第二行包含 N N N 个整数: A 1 , A 2 , A 3 , … , A N A_{1}, A_{2}, A_{3}, \ldots, A_{N} A1,A2,A3,…,AN.
【输出格式】
输出 N N N 个整数, 依次表示第 1 … N 1 \ldots N 1…N 号学生分别至少还要再刷多少道题。
【样例输入】
5 \begin{array}{lllll}5\end{array} 5
12 10 15 20 6 \begin{array}{lllll}12 & 10& 15& 20& 6\end{array} 121015206
【样例输出】
0 3 0 0 7 \begin{array}{lllll}0 & 3 & 0 & 0 & 7\end{array} 03007
【评测用例规模与约定】
对于 30 % 30 \% 30% 的数据, 1 ≤ N ≤ 1000 , 0 ≤ A i ≤ 1000 1 \leq N \leq 1000,0 \leq A_{i} \leq 1000 1≤N≤1000,0≤Ai≤1000.
对于 100 % 100 \% 100% 的数据, 1 ≤ N ≤ 100000 , 0 ≤ A i ≤ 100000 1 \leq N \leq 100000,0 \leq A_{i} \leq 100000 1≤N≤100000,0≤Ai≤100000.
试题 E \mathrm{E} E : 求阶乘
时间限制: 1.0 s 1.0 \mathrm{~s} 1.0 s 内存限制: 512.0 M B 512.0 \mathrm{MB} 512.0MB 本题总分: 15 分
【问题描述】
满足 N ! N ! N! 的末尾恰好有 K K K 个 0 的最小的 N N N 是多少?如果这样的 N N N 不存在输出 -1 。
【输入格式】
一个整数 K K K 。
【输出格式】
一个整数代表答案。
【样例输入】
2 \begin{array}{lllll}2\end{array} 2
【样例输出】
10 \begin{array}{lllll}10\end{array} 10
【评测用例规模与约定】
对于 30 % 30 \% 30% 的数据, 1 ≤ K ≤ 1 0 6 1 \leq K \leq 10^{6} 1≤K≤106.
对于 100 % 100 \% 100% 的数据, 1 ≤ K ≤ 1 0 18 1 \leq K \leq 10^{18} 1≤K≤1018.
试题 F : \mathrm{F}: F: 最大子矩阵
时间限制: 1.0 s 1.0 \mathrm{~s} 1.0 s 内存限制: 512.0 M B 512.0 \mathrm{MB} 512.0MB 本题总分: 15 分
【问题描述】
小明有一个大小为 N × M N \times M N×M 的矩阵, 可以理解为一个 N N N 行 M M M 列的二维数组。我们定义一个矩阵 m m m 的稳定度 f ( m ) f(m) f(m) 为 f ( m ) = max ( m ) − min ( m ) f(m)=\max (m)-\min (m) f(m)=max(m)−min(m), 其中 max ( m ) \max (m) max(m)表示矩阵 m m m 中的最大值, min ( m ) \min (m) min(m) 表示矩阵 m m m 中的最小值。现在小明想要从这个矩阵中找到一个稳定度不大于 limit 的子矩阵, 同时他还希望这个子矩阵的面积越大越好 (面积可以理解为矩阵中元素个数)。
子矩阵定义如下: 从原矩阵中选择一组连续的行和一组连续的列, 这些行列交点上的元素组成的矩阵即为一个子矩阵。
【输入格式】
第一行输入两个整数 N , M N, M N,M, 表示矩阵的大小。
接下来 N N N 行, 每行输入 M M M 个整数, 表示这个矩阵。
最后一行输入一个整数 limit, 表示限制。
【输出格式】
输出一个整数, 分别表示小明选择的子矩阵的最大面积。
【样例输入】
3 4 \begin{array}{lllll} 3 &4\end{array} 34
2 0 7 9 \begin{array}{llll}2 & 0 & 7 & 9\end{array} 2079
0 6 9 7 \begin{array}{llll}0 & 6 & 9 & 7\end{array} 0697
8 4 6 4 \begin{array}{llll}8 & 4 & 6 & 4\end{array} 8464
8 \begin{array}{lllll}8\end{array} 8
【样例输出】
6 \begin{array}{lllll}6\end{array} 6
【样例说明】
满足稳定度不大于 8 的且面积最大的子矩阵总共有三个, 他们的面积都是 6 (粗体表示子矩阵元素):
2 7 0 9 \begin{array}{lllll}2& 7& 0 & 9\end{array} 2709
0 6 9 7 \begin{array}{lllll}0& 6&9 & 7\end{array} 0697
8 4 6 4 \begin{array}{lllll}8& 4& 6& 4\end{array} 8464
\begin{array}{lllll}\end{array}
2 7 0 9 \begin{array}{lllll}2& 7& 0 & 9\end{array} 2709
0 6 9 7 \begin{array}{lllll}0& 6& 9& 7\end{array} 0697
8 4 6 4 \begin{array}{lllll}8& 4& 6& 4\end{array} 8464
\begin{array}{lllll}\end{array}
2 7 0 9 \begin{array}{lllll}2& 7& 0 & 9\end{array} 2709
0 6 9 7 \begin{array}{lllll}0& 6&9 & 7\end{array} 0697
8 4 6 4 \begin{array}{lllll}8& 4& 6& 4\end{array} 8464
【评测用例规模与约定】
| 评测用例编号 | N \mathrm{N} N | M \mathrm{M} M |
|---|---|---|
| 1,2 | 1 ≤ N ≤ 10 1 \leq N \leq 10 1≤N≤10 | 1 ≤ M ≤ 10 1 \leq M \leq 10 1≤M≤10 |
| 3,4 | N = 1 N=1 N=1 | M ≤ 100000 M \leq 100000 M≤100000 |
| 5 ∼ 12 5 \sim 12 5∼12 | 1 ≤ N ≤ 10 1 \leq N \leq 10 1≤N≤10 | M ≤ 10000 M \leq 10000 M≤10000 |
| 13 ∼ 20 13 \sim 20 13∼20 | 1 ≤ N ≤ 80 1 \leq N \leq 80 1≤N≤80 | 1 ≤ M ≤ 80 1 \leq M \leq 80 1≤M≤80 |
对于所有评测用例, 0 ≤ 0 \leq 0≤ 矩阵元素值, limit ≤ 1 0 5 \leq 10^{5} ≤105 。
试题 G: 数组切分
时间限制: 1.0 s 1.0 \mathrm{~s} 1.0 s 内存限制: 512.0 M B 512.0 \mathrm{MB} 512.0MB 本题总分:20 分
【问题描述】
已知一个长度为 N N N 的数组: A 1 , A 2 , A 3 , … A N A_{1}, A_{2}, A_{3}, \ldots A_{N} A1,A2,A3,…AN 恰好是 1 ∼ N 1 \sim N 1∼N 的一个排列。现在要求你将 A A A 数组切分成若干个 (最少一个, 最多 N N N 个) 连续的子数组, 并且每个子数组中包含的整数恰好可以组成一段连续的自然数。
例如对于 A = { 1 , 3 , 2 , 4 } A=\{1,3,2,4\} A={1,3,2,4}, 一共有 5 种切分方法:
{ 1 } { 3 } { 2 } 4 } : \{1\} \{3\}\{2\} 4\}: {1}{3}{2}4}: 每个单独的数显然是 (长度为 1 的) 一段连续的自然数。
{ 1 } { 3 , 2 } 4 } : { 3 , 2 } \{1\} \{3,2\} 4\}:\{3,2\} {1}{3,2}4}:{3,2} 包含 2 到 3 , 是一段连续的自然数, 另外 { 1 } \{1\} {1} 和 { 4 } \{4\} {4} 显然也是。
{ 1 } { 3 , 2 , 4 } : { 3 , 2 , 4 } \{1\}\{3,2,4\}:\{3,2,4\} {1}{3,2,4}:{3,2,4} 包含 2 到 4 , 是一段连续的自然数, 另外 { 1 } \{1\} {1} 显然也是。
{ 1 , 3 , 2 } { 4 } : { 1 , 3 , 2 } \{1,3,2\} \{4\}:\{1,3,2\} {1,3,2}{4}:{1,3,2} 包含 1 到 3 , 是一段连续的自然数, 另外 { 4 } \{4\} {4} 显然也是。
{ 1 , 3 , 2 , 4 } \{1,3,2,4\} {1,3,2,4} : 只有一个子数组, 包含 1 到 4 , 是一段连续的自然数。
【输入格式】
第一行包含一个整数 N N N 。第二行包含 N N N 个整数, 代表 A A A 数组。
【输出格式】
输出一个整数表示答案。由于答案可能很大, 所以输出其对 1000000007 取模后的值
【样例输入】
4 \begin{array}{llll} 4\end{array} 4
1 3 2 4 \begin{array}{llll}1 & 3 & 2 & 4\end{array} 1324
【样例输出】
5 \begin{array}{llll}5\end{array} 5
【评测用例规模与约定】
对于 30 % 30 \% 30% 评测用例, 1 ≤ N ≤ 20 1 \leq N \leq 20 1≤N≤20.
对于 100 % 100 \% 100% 评测用例, 1 ≤ N ≤ 10000 1 \leq N \leq 10000 1≤N≤10000.
试题 H: 回忆迷宫
时间限制: 1.0 s 1.0 \mathrm{~s} 1.0 s 内存限制: 512.0 M B 512.0 \mathrm{MB} 512.0MB 本题总分: 20 分
【问题描述】
爱丽丝刚从一处地下迷宫中探险归来, 你能根据她对于自己行动路径的回讴, 帮她画出迷宫地图吗?
迷宫地图是基于二维网格的。爱丽丝会告诉你一系列她在迷宫中的移动步骤, 每个移动步骤可能是上下左右四个方向中的一种, 表示爱丽丝往这个方向走了一格。你需要根据这些移动步骤给出一个迷宫地图, 并满足以下条件:
1、爱丽丝能在迷宫内的某个空地开始, 顺利的走完她回忆的所有移动步骤。
2、迷宫内不存在爱丽丝没有走过的空地。
3、迷宫是封闭的,即可通过墙分隔迷宫内与迷宫外。任意方向的无穷远处视为迷宫外, 所有不与迷宫外联通的空地都视为是迷宫内。(迷宫地图为四联通, 即只有上下左右视为联通)
4、在满足前面三点的前提下, 迷宫的墙的数量要尽可能少。
【输入格式】
第一行一个正整数 N N N, 表示爱丽丝回忆的步骤数量。
接下来一行 N N N 个英文字符, 仅包含 UDLR 四种字符, 分别表示上 (Up)、下 (Down)、左 (Left)、右 (Right)。
【输出格式】
请通过字符画的形式输出迷宫地图。迷宫地图可能包含许多行, 用字符 '*’表示墙, 用“(空格)表示非墙。
你的输出需要保证以下条件:
1、至少有一行第一个字符为 ‘*’。
2、第一行至少有一个字符为 ‘*’。
3、每一行的最后一个字符为 ‘*’。
4、最后一行至少有一个字符为 ‘*’。
【样例输入】
17
UUUULLLLDDDDRRRRU
【样例输出】

【样例说明】
爱丽丝可以把第六行第六个字符作为起点。

【评测用例规模与约定】
对于所有数据, 0 < N ≤ 100 0<N \leq 100 0<N≤100.
试题 I: 红绿灯
时间限制: 1.0 s 1.0 \mathrm{~s} 1.0 s 内存限制: 512.0 M B 512.0 \mathrm{MB} 512.0MB 本题总分: 25 分
【问题描述】
爱丽丝要开车去上班, 上班的路上有许多红绿灯, 这让爱丽丝很难过。为了上班不迟到, 她给自己的车安装了氮气喷射装置。现在她想知道自己上班最短需要多少时间。
爱丽丝的车最高速度是 1 V \frac{1}{V} V1 米每秒, 并且经过改装后, 可以瞬间加速到小于等于最高速的任意速度, 也可以瞬间停止。
爱丽丝家离公司有 N N N 米远, 路上有 M M M 个红绿灯, 第 i 个红绿灯位于离爱丽丝家 A i A_{i} Ai 米远的位置, 绿灯持续 B i B_{i} Bi 秒, 红灯持续 C i C_{i} Ci 秒。在初始时(爱丽丝开始计时的瞬间), 所有红绿灯都恰好从红灯变为绿灯。如果爱丽丝在绿灯变红的瞬间到达红绿灯,她会停下车等红灯,因为她是遵纪守法的好市民。
氮气喷射装置可以让爱丽丝的车瞬间加速到超光速(且不受相对论效应的影响!), 达到瞬移的效果, 但是爱丽丝是遵纪守法的好市民, 在每个红绿灯前她都会停下氮气喷射, 即使是绿灯, 因为红绿灯处有斑马线, 而使用氮气喷射装置通过斑马线是违法的。此外, 氮气喷射装置不能连续启动, 需要一定时间的冷却, 表现为通过 K K K 个红绿灯后才能再次使用。(也就是说, 如果 K = 1 K=1 K=1, 就能一直使用啦!) 初始时, 氮气喷射装置处于可用状态。
【输入格式】
第一行四个正整数 N 、 M 、 K 、 V , N 、 M 、 K 、 V , N、M、K、V, 含义如题面所述。
接下来 M M M 行, 每行三个正整数 A i 、 B i 、 C i A_{i} 、 B_{i} 、 C_{i} Ai、Bi、Ci, 含义如题面所述。
【输出格式】
输出一个正整数 T,表示爱丽丝到达公司最短需要多少秒。
【样例输入】
90 2 2 2 \begin{array}{llll}90& 2& 2 & 2\end{array} 90222
30 20 20 \begin{array}{llll}30& 20& 20 \end{array} 302020
60 20 20 \begin{array}{llll}60& 20& 20 \end{array} 602020
【样例输出】
80 \begin{array}{llll}80\end{array} 80
【样例说明】
爱丽丝在最开始直接使用氮气喷射装置瞬间到达第一个红绿灯, 然后绿灯通过, 以最高速行进 60 秒后到达第二个红绿灯, 此时绿灯刚好变红, 于是她等待 20 秒再次变为绿灯后通过该红绿灯, 此时氮气喷射装置冷却完毕, 爱丽丝再次使用瞬间到达公司, 总共用时 80 秒。
【评测用例规模与约定】
对于 30 % 30 \% 30% 的数据, N ≤ 100 ; M ≤ 10 ; M < K ; V = 1 N \leq 100 ; M \leq 10 ; M<K ; V=1 N≤100;M≤10;M<K;V=1
对于 60 % 60 \% 60% 的数据, N ≤ 1000 ; M ≤ 100 ; K ≤ 50 ; B i , C i ≤ 100 ; V ≤ 10 N \leq 1000 ; M \leq 100 ; K \leq 50 ; B_{i}, C_{i} \leq 100 ; V \leq 10 N≤1000;M≤100;K≤50;Bi,Ci≤100;V≤10.
对于 100 % 100 \% 100% 的数据, 0 < N ≤ 1 0 8 ; M ≤ 1000 ; K ≤ 1000 ; 0 < B i , C i ≤ 1 0 6 ; 0 < 0<N \leq 10^{8} ; M \leq 1000 ; K \leq 1000 ; 0<B_{i}, C_{i} \leq 10^{6} ; 0< 0<N≤108;M≤1000;K≤1000;0<Bi,Ci≤106;0< V ≤ 1 0 6 ; 0 < A i < N V \leq 10^{6} ; 0<A_{i}<N V≤106;0<Ai<N; 对任意 i < j i<j i<j, 有 A i < A j A_{i}<A_{j} Ai<Aj
试题 J 拉箱子
时间限制: 1.0 s 1.0 \mathrm{~s} 1.0 s 内存限制: 1.0 G B 1.0 \mathrm{~GB} 1.0 GB 本题总分: 25 分
【问题描述】
推箱子是一款经典电子游戏, 爱丽丝很喜欢玩, 但是她有点玩淢了, 现在她想设计一款拉箱子游戏。
拉箱子游戏需要玩家在一个 N × M N \times M N×M 的网格地图中, 控制小人上下左右移动,将箱子拉到终点以获得胜利。
现在爱丽丝想知道, 在给定地形 (即所有墙的位置) 的情况下, 有多少种不同的可解的初始局面。
【初始局面】的定义如下:
1、初始局面由排列成 N × M N \times M N×M 矩形网格状的各种元素组成, 每个网格中有且只有一种元素。可能的元素有: 空地、墙、小人、箱子、终点。
2、初始局面中有且只有一个小人。
3、初始局面中有且只有一个箱子。
4、初始局面中有且只有一个终点。
【可解】的定义如下:
通过有限次数的移动小人 (可以在移动的同时拉箱子), 箱子能够到达终点所在的网格。
【移动】的定义如下:
在一次移动中, 小人可以移动到相邻 (上、下、左、右四种选项) 的一个网格中, 前提是满足以下条件:
1、小人永远不能移动到 N × M N \times M N×M 的网格外部。
2、小人永远不能移动到墙上或是箱子上。
3、小人可以移动到空地或是终点上。
【拉箱子】的定义如下:
在一次合法移动的同时, 如果小人初始所在网格沿小人移动方向的反方向
上的相邻网格上恰好是箱子, 小人可以拉动箱子一起移动, 让箱子移动到小人初始所在网格。
即使满足条件,小人也可以只移动而不拉箱子。
【输入格式】
第一行两个正整数 N N N 和 M M M, 表示网格的大小。
接下来 N N N 行, 每行 M M M 个由空格隔开的整数 0 或 1 描述给定的地形。其中 1 表示墙, 0 表示未知的元素, 未知元素可能是小人或箱子或空地或终点, 但不能是墙。
【输出格式】
输出一个正整数, 表示可解的初始局面数量。
【样例输入】
2 4 \begin{array}{llll}2 & 4\end{array} 24
0 0 0 0 \begin{array}{llll}0 & 0 & 0 & 0\end{array} 0000
1 1 1 0 \begin{array}{llll}1 & 1 & 1 & 0\end{array} 1110
【样例输出】
13 \begin{array}{llll}13\end{array} 13
【样例说明】



【评测用例规模与约定】
对于 30 % 30 \% 30% 的数据, N , M ≤ 3 N, M \leq 3 N,M≤3.
对于 100 % 100 \% 100% 的数据, 0 < N , M ≤ 10 0<N, M \leq 10 0<N,M≤10.
相关文章:

第十三届蓝桥杯省赛真题 Java B 组【原卷】
文章目录 发现宝藏【考生须知】试题 A: 星期计算试题 B: 山试题 C: 字符统计试题 D: 最少刷题数试题 E \mathrm{E} E : 求阶乘试题 F : \mathrm{F}: F: 最大子矩阵试题 G: 数组切分试题 H: 回忆迷宫试题 I: 红绿灯试题 J 拉箱子 发现宝藏 前些天发现了一个巨牛的人工智能学习…...
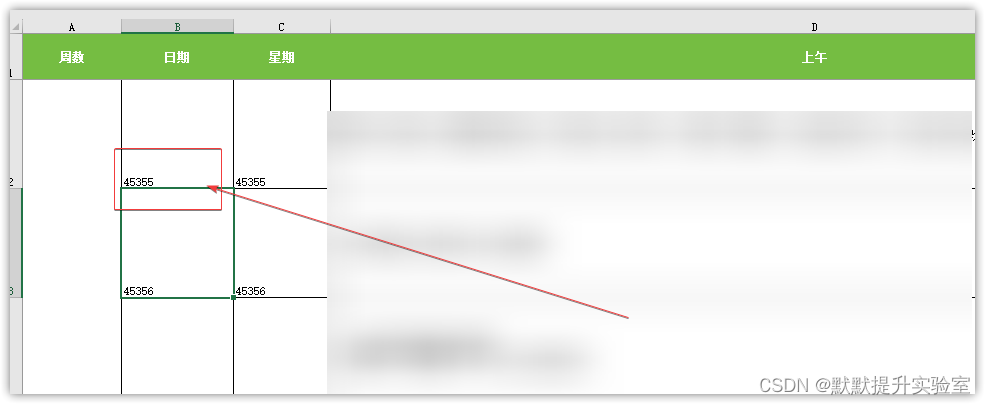
Excel 打开后提示:MicrosoftExcel无法计算某个公式。在打开的工作簿中有一个循环引用...
目录预览 一、问题描述二、原因分析三、解决方案四、参考链接 一、问题描述 MicrosoftExcel无法计算某个公式。在打开的工作簿中有一个循环引用,但无法列出导致循环的引I用。请尝试编辑上次输入的公式,或利用“撤消”命令删除该公式,如下图&…...
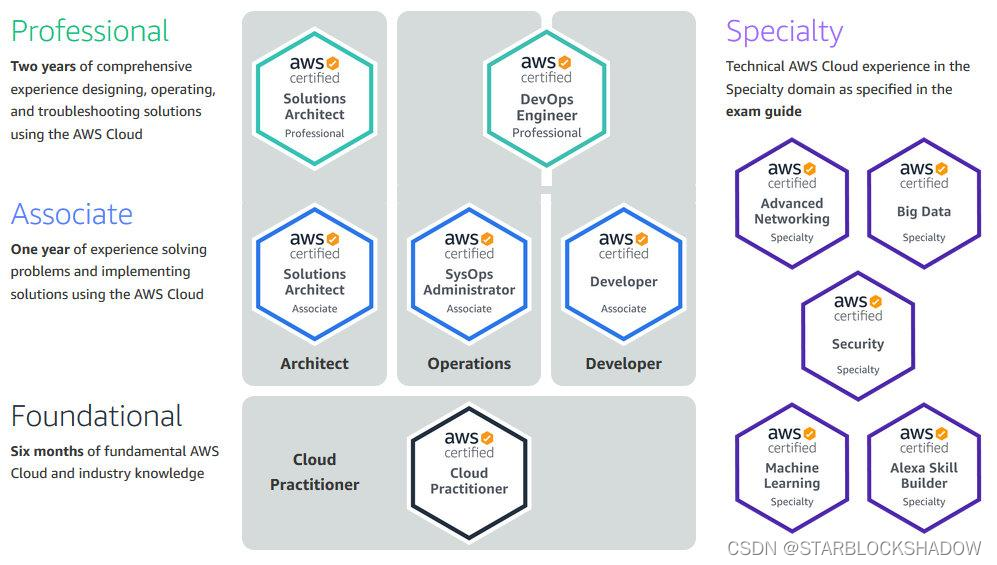
【自我提升】计算机领域相关证书
目录 计算机技术与软件专业资格(水平)考试证书(软考)Oracle认证Cisco认证微软认证红帽认证AWS认证 计算机技术与软件专业资格(水平)考试证书(软考) 计算机技术与软件专业技术资格&a…...
外包干了15天,技术退步明显。。。。。
先说一下自己的情况,本科生,2019年我通过校招踏入了南京一家软件公司,开始了我的职业生涯。那时的我,满怀热血和憧憬,期待着在这个行业中闯出一片天地。然而,随着时间的推移,我发现自己逐渐陷入…...

人工智能(Educoder)-- 搜索技术 -- 启发式搜索
任务描述 本关任务:八数码问题是在一个33的棋盘上有1−8位数字随机分布,以及一个空格,与空格相连的棋子可以滑动到空格中,问题的解是通过空格滑动,使得棋盘转化为目标状态,如下图所示。 为了简化问题的输…...
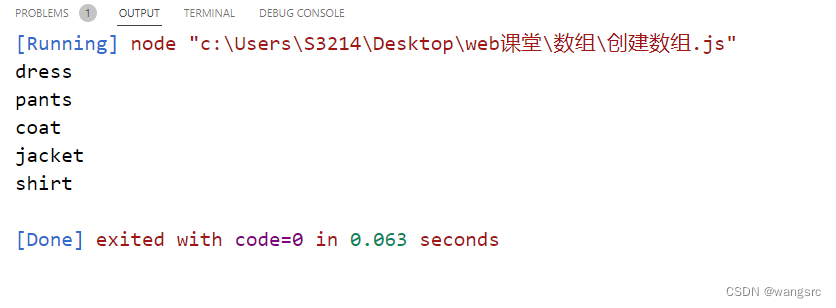
计算平均分 javascript
养成好习惯:先写注释再写代码 基础版:直接写逻辑(平均分总和/个数) // 求平均分 var scores [60, 55, 80, 33, 75, 100]; // 求和,相除 var sum 0; var avg;for (var i 0; i < 6; i) {sum scores[i]; }avg sum / 6; con…...
Redis入门到实战-第三弹
Redis入门到实战 Redis数据类型官网地址Redis概述Redis数据类型介绍更新计划 Redis数据类型 官网地址 声明: 由于操作系统, 版本更新等原因, 文章所列内容不一定100%复现, 还要以官方信息为准 https://redis.io/Redis概述 Redis是一个开源的(采用BSD许可证&#…...
AnyGo for Mac最新激活版:位置模拟软件打破地域限制
AnyGo for Mac,一款专为Mac用户打造的位置模拟软件,让您能够轻松打破地域限制,畅享无限可能。 软件下载:AnyGo for Mac v7.0.0最新激活版 通过AnyGo,您可以随时随地模拟出任何地理位置,无论是国内热门景点还…...

【Mysql数据库基础07】DDL 数据定义语言
Data Definition Language 1 库的操作1.1 create 创建1.2 alter 修改1.3 drop 删除 2 表的操作2.1 表的创建2.2 表的修改2.2.1 修改表名2.2.2 修改列名2.2.3 修改列的类型和约束2.2.4 添加列2.2.5 删除列 2.3 表的删除2.4 表的复制 3 练习 1 库的操作 1.1 create 创建 create…...

数据库及中表的创建和管理
目录 创建数据库 使用数据库(使用,查看信息) 修改数据库(删除,修改)...

git笔记之撤销、回退、reset方面的笔记
git笔记之撤销、回退、reset方面的笔记 code review! 文章目录 git笔记之撤销、回退、reset方面的笔记1.git 已经commit了,还没push,如何撤销到初始状态git reset --soft HEAD~1git reset HEAD~1(等同于 git reset --mixed HEAD~1࿰…...

【中间件】docker数据卷
📝个人主页:五敷有你 🔥系列专栏:中间件 ⛺️稳中求进,晒太阳 1.数据卷(容器数据管理) 修改nginx的html页面时,需要进入nginx内部。并且因为内部没有编辑器,修改…...
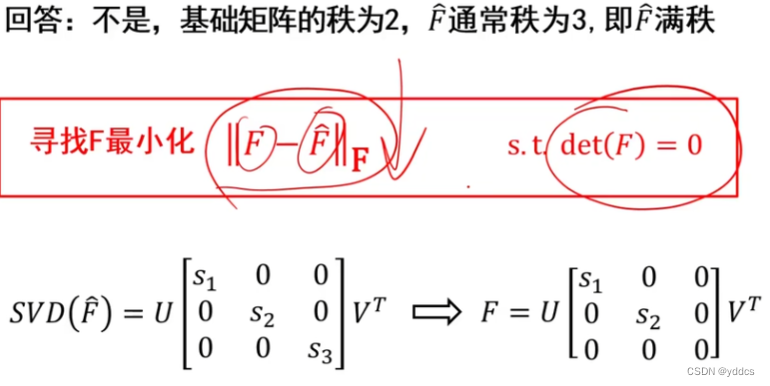
【3D reconstruction 学习笔记 第二部】
三维重建 3D reconstruction 4. 三维重建与极几何三角化(线性解法)三角化(非线性解法)多视图几何极几何极几何约束基础矩阵估计 5. 双目立体视觉重建6. 多视图重建7. SFM 系统设计8. SLAM系统设计 4. 三维重建与极几何 三角化&…...
)
【CSP试题回顾】202109-1-数组推导(优化)
CSP-202109-1-数组推导 解题代码 #include <iostream> #include <vector> #include <algorithm> using namespace std;long long n, sumMax,sumMin;int main() {cin >> n;vector<long long>arr(n);for (size_t i 0; i < n; i){cin >>…...

Redis - 高并发场景下的Redis最佳实践_翻过6座大山
文章目录 概述6座大山之_缓存雪崩 (缓存全部失效)缓存雪崩的两种常见场景如何应对缓存雪崩? 6座大山之_缓存穿透(查询不存在的 key)缓存穿透的原因解决方案1. 数据校验2. 缓存空值3. 频控4. 使用布隆过滤器 6座大山之_…...

数字乡村发展策略:科技引领农村实现跨越式发展
随着信息技术的迅猛发展和数字经济的崛起,数字乡村发展策略已经成为引领农村实现跨越式发展的重要手段。科技的力量正在深刻改变着传统农业的生产方式、农村的社会结构以及农民的生活方式,为农村经济发展注入了新的活力和动力。本文将从数字乡村的内涵、…...
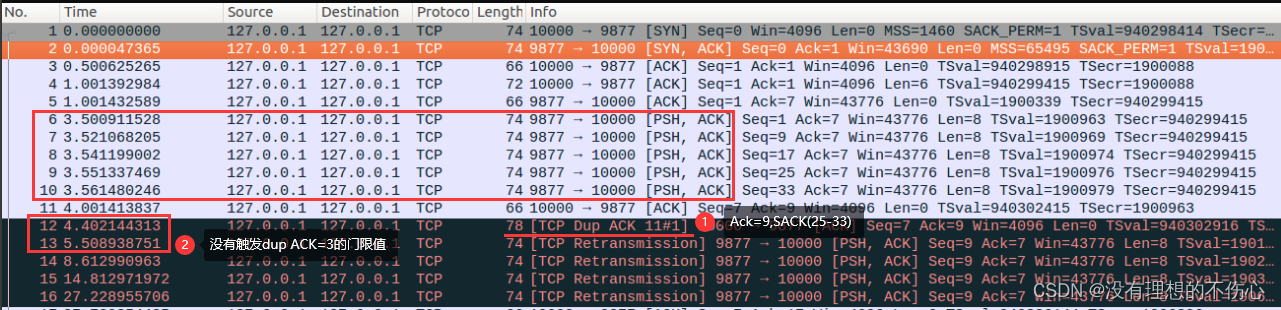
TCP重传机制详解——04FACK
文章目录 TCP重传机制详解——04FACK什么是FACKFACK的发展为什么要引入FACK实战抓包讲解开启FACK场景,且达到dup ACK门限值开启FACK场景,未达到dup ACK门限值 为什么要淘汰FACK总结REF TCP重传机制详解——04FACK 什么是FACK FACK的全称是forward ackn…...

安卓Java面试题 206- 210
206. 简述如何统计Activity的工作时间 ?如何统计Activity启动所用的时间? 可以通过分析Log得到(这个就是DDMS的那个Log)。 当我们点击触摸时会了类似以下的Log A: 03-06 03:36:47.865: VERBOSE/InputDevice(2486): ID[0]=0(0) Dn (0=>1) 03-06 03:36:47.865: INFO/Powe…...
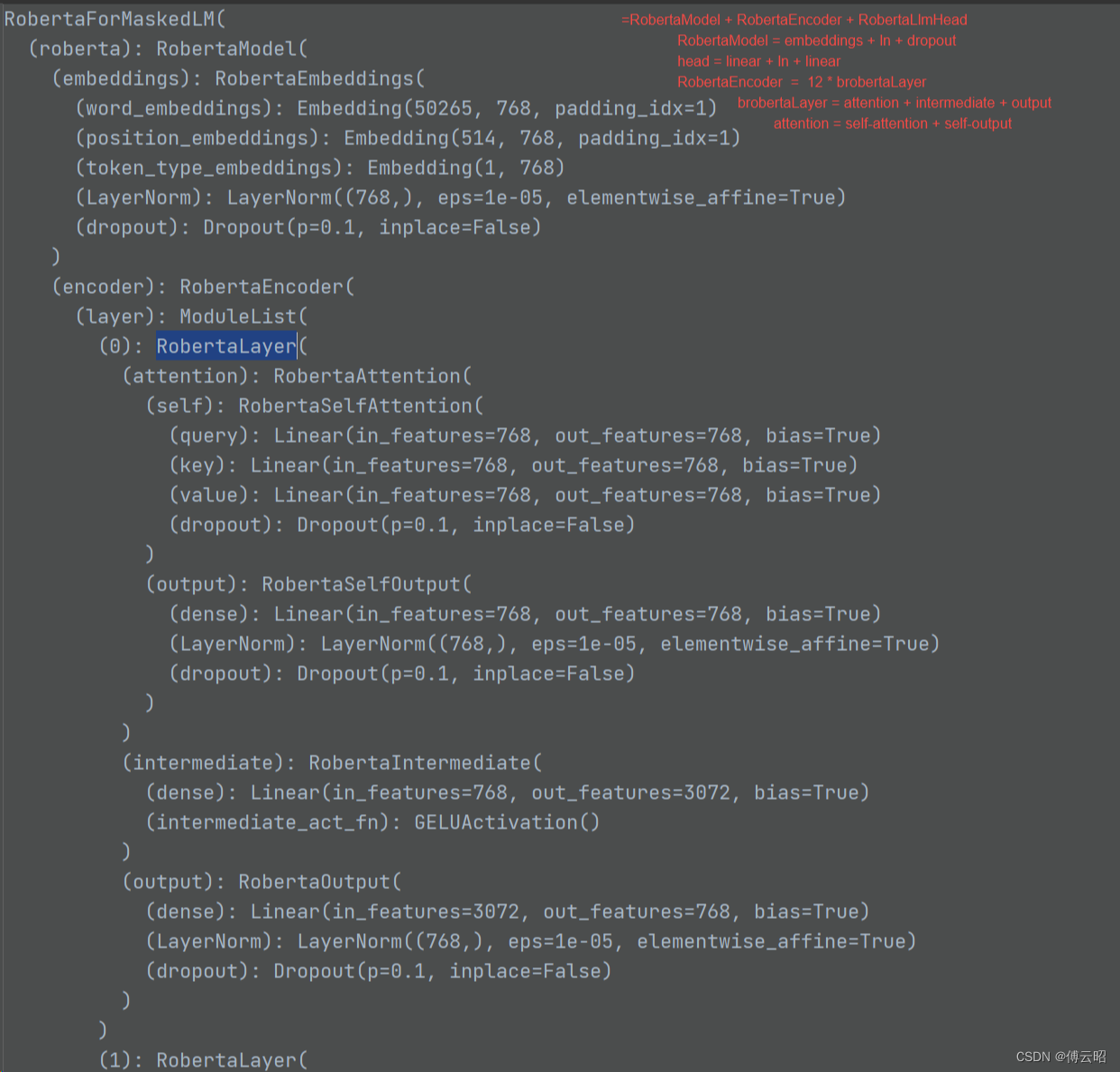
huggingface的transformers训练bert
目录 理论 实践 理论 https://arxiv.org/abs/1810.04805 BERT(Bidirectional Encoder Representations from Transformers)是一种自然语言处理(NLP)模型,由Google在2018年提出。它是基于Transformer模型的预训练方法…...
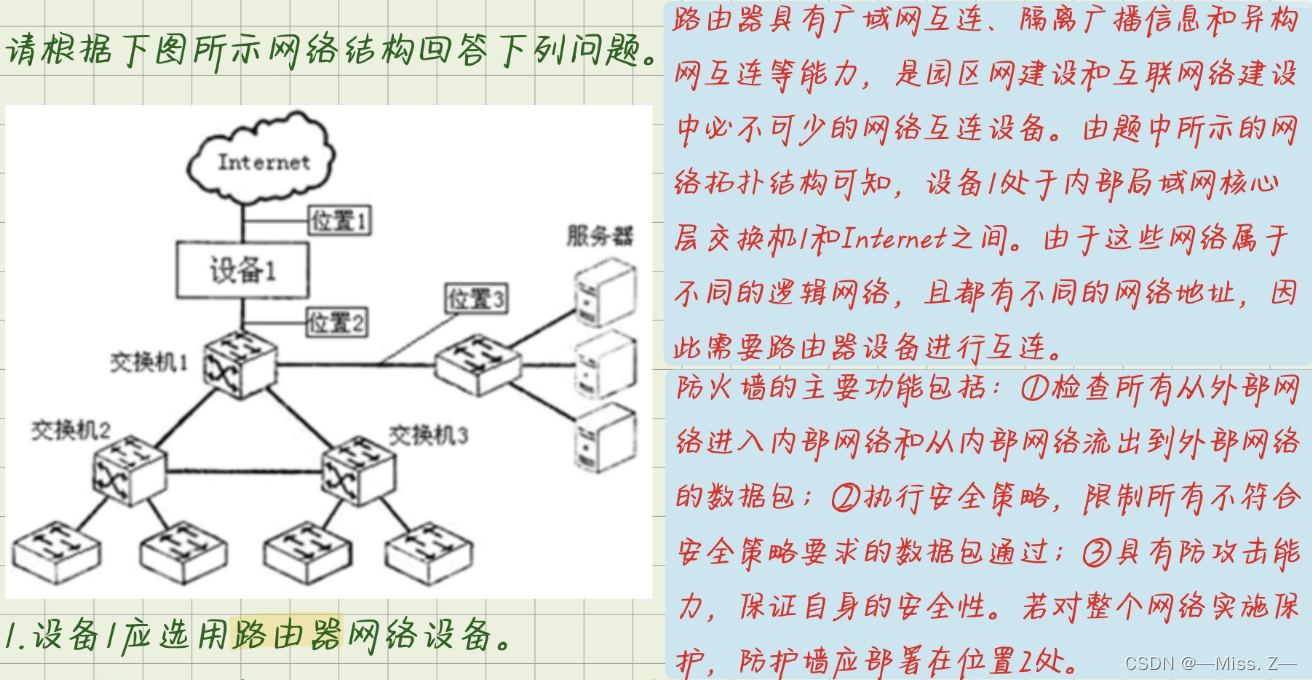
计算机三级——网络技术(综合题第五题)
第一题 填写路由器RG的路由表项①至④。 目的网络/掩码长度输出端口输出端口172.19.63.192/30S0(直接连接)172.19.63.188/30S1(直接连接) 路由器RG的S0的IP地址是172.19.63.193,路由器RE的S0的IP地址是172.19.63.194。 【解析】…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...
