【机器学习】无监督学习算法之:K均值聚类
K均值聚类
- 1、引言
- 2、K均值聚类
- 2.1 定义
- 2.2 原理
- 2.3 实现方式
- 2.4 算法公式
- 2.4.1 距离计算公式
- 2.4.1 中心点计算公式
- 2.5 代码示例
- 3、总结
1、引言
小屌丝:鱼哥, K均值聚类 我不懂,能不能给我讲一讲?
小鱼:行,可以
小屌丝:额…今天咋直接就答应了?
小鱼:不然呢?
小屌丝:有啥条件,直接说,
小鱼:没有
小屌丝:这咋的了,不提条件,我可不踏实
小鱼:你看看你, 我不提条件,你还不踏实,那你这是非让我提条件呗
小屌丝:我…这…我…
小鱼:既然你都让我提条件了,那我就说吧
小屌丝: …
小鱼:最近好长时间没撸串了哈。
小屌丝:…

小鱼:你看看,让我提条件, 还这表情。那算了。
小屌丝:别别别, 可以可以。
小鱼: 这是,可以去吃,还是别提条件?
小屌丝:去撸串> <
2、K均值聚类
2.1 定义
K均值聚类是一种无监督学习算法,旨在将数据划分为K个不相交的簇,使得每个数据点都属于离其最近的簇的质心。
质心是每个簇中所有数据点的平均值,代表该簇的中心位置。
2.2 原理
K均值聚类的原理基于迭代优化。
- 算法首先随机选择K个初始质心,然后将每个数据点分配给最近的质心所在的簇。
- 接下来,算法重新计算每个簇的质心位置,即该簇内所有数据点的平均值。
这个过程不断重复,直到满足某个停止条件,如质心位置不再发生显著变化或达到最大迭代次数。
2.3 实现方式
K均值聚类的实现主要包括以下步骤:
- 初始化:随机选择K个数据点作为初始质心。
- 分配数据点到簇:对于每个数据点,计算其与所有质心的距离,并将其分配给最近的质心所在的簇。
- 更新质心:对于每个簇,重新计算其质心位置,即该簇内所有数据点的平均值。
- 重复迭代:重复步骤2和3,直到质心位置不再发生显著变化或达到最大迭代次数。
2.4 算法公式
2.4.1 距离计算公式
对于每个数据点,计算其与每个中心点之间的距离。常用的距离计算公式是欧氏距离公式:
d ( x , y ) = s q r t ( ( x 1 − y 1 ) 2 + ( x 2 − y 2 ) 2 + … + ( x n − y n ) 2 ) d(x, y) = sqrt((x1-y1)^2 + (x2-y2)^2 + … + (xn-yn)^2) d(x,y)=sqrt((x1−y1)2+(x2−y2)2+…+(xn−yn)2)
其中, x x x和 y y y分别表示两个数据点的特征向量, n n n表示特征的维度。
2.4.1 中心点计算公式
中心点更新公式: C k = ( 1 / ∣ S k ∣ ) ∗ Σ x i Ck = (1/|Sk|) * Σxi Ck=(1/∣Sk∣)∗Σxi
其中 C k Ck Ck为第 k k k个类别的中心点, S k Sk Sk为第 k k k个类别中的数据点集合。
2.5 代码示例
# -*- coding:utf-8 -*-
# @Time : 2024-03-13
# @Author : Carl_DJ'''
实现功能:实scikit-learn库实现K均值聚类'''
import numpy as np # 假设我们有一个二维数据集X
X = np.array([[1, 2], [1, 4], [1, 0], [10, 2], [10, 4], [10, 0]]) # 设定簇的数量
K = 2 # 步骤1: 初始化质心
# 随机选择K个数据点作为初始质心
np.random.seed(0) # 为了可重复性设置随机种子
initial_centroids = X[np.random.choice(range(X.shape[0]), K, replace=False)]
centroids = initial_centroids # 迭代过程
max_iterations = 100 # 最大迭代次数
tolerance = 1e-4 # 收敛阈值
has_converged = False
iteration = 0 while not has_converged and iteration < max_iterations: # 步骤2: 分配数据点到簇 # 对于每个数据点,计算其与所有质心的距离,并将其分配给最近的质心所在的簇 labels = [] for x in X: distances = np.linalg.norm(x - centroids, axis=1) label = np.argmin(distances) labels.append(label) labels = np.array(labels) # 旧的质心位置,用于收敛性检查 old_centroids = centroids.copy() # 步骤3: 更新质心 # 对于每个簇,重新计算其质心位置,即该簇内所有数据点的平均值 new_centroids = np.array([X[labels == i].mean(axis=0) for i in range(K)]) centroids = new_centroids # 步骤4: 检查收敛性 # 如果质心不再发生显著变化,则算法收敛 if np.allclose(old_centroids, centroids, atol=tolerance): has_converged = True iteration += 1 # 输出结果
print("Iterations:", iteration)
print("Labels:", labels)
print("Centroids:", centroids)代码解析
实现K均值聚类的完整过程:
-
初始化质心:通过np.random.choice随机选择K个数据点作为初始质心。
-
分配数据点到簇:对于数据集中的每个数据点,我们计算它与所有质心的距离,并将其分配给最近的质心所在的簇。这通过遍历数据点,计算每个点到所有质心的欧几里得距离,并找到最近的质心来完成。
-
更新质心:对于每个簇,我们计算该簇内所有数据点的平均值作为新的质心位置。这通过分组数据点(基于它们的簇标签)并计算每组的平均值来实现。
-
检查收敛性:我们检查新的质心位置是否与旧的质心位置非常接近(在容忍度范围内)。如果是,则算法已经收敛,可以停止迭代。否则,我们继续迭代过程。
-
重复迭代:如果算法没有收敛,我们重复步骤2到步骤4,直到达到最大迭代次数或算法收敛为止。

3、总结
K均值聚类是一种简单而有效的无监督学习算法,能够自动将数据划分为K个不同的簇。
通过迭代优化过程,算法将数据点分配给最近的质心,并重新计算质心位置,直到满足停止条件。
K均值聚类在数据处理、图像分割和模式识别等领域具有广泛的应用。
然而,它也有一些局限性,如对初始质心的选择敏感、可能陷入局部最优解等。
在实际应用中,需要根据具体任务和数据特点选择合适的算法和参数。
我是小鱼:
- CSDN 博客专家;
- 阿里云 专家博主;
- 51CTO博客专家;
- 企业认证金牌面试官;
- 多个名企认证&特邀讲师等;
- 名企签约职场面试培训、职场规划师;
- 多个国内主流技术社区的认证专家博主;
- 多款主流产品(阿里云等)测评一、二等奖获得者;
关注小鱼,学习机器学习领域的知识。
相关文章:

【机器学习】无监督学习算法之:K均值聚类
K均值聚类 1、引言2、K均值聚类2.1 定义2.2 原理2.3 实现方式2.4 算法公式2.4.1 距离计算公式2.4.1 中心点计算公式 2.5 代码示例 3、总结 1、引言 小屌丝:鱼哥, K均值聚类 我不懂,能不能给我讲一讲? 小鱼:行…...

为wordpress特定分类目录下的内容添加自定义字段
在WordPress中,您可以使用自定义字段(Custom Fields)或称为元数据(Meta Data)来为特定分类目录下的内容添加额外的信息。自定义字段可以附加到文章、页面、用户和其他对象上。以下是一个逐步指南,介绍如何为特定分类目录下的内容添加自定义字段ÿ…...
javaWeb在线考试系统
一、简介 在线考试系统是现代教育中一项重要的辅助教学工具,它为学生提供了便捷的考试方式,同时也为教师提供了高效的考试管理方式。我设计了一个基于JavaWeb的在线考试系统,该系统包括三个角色:管理员、老师和学生。管理员拥有菜…...
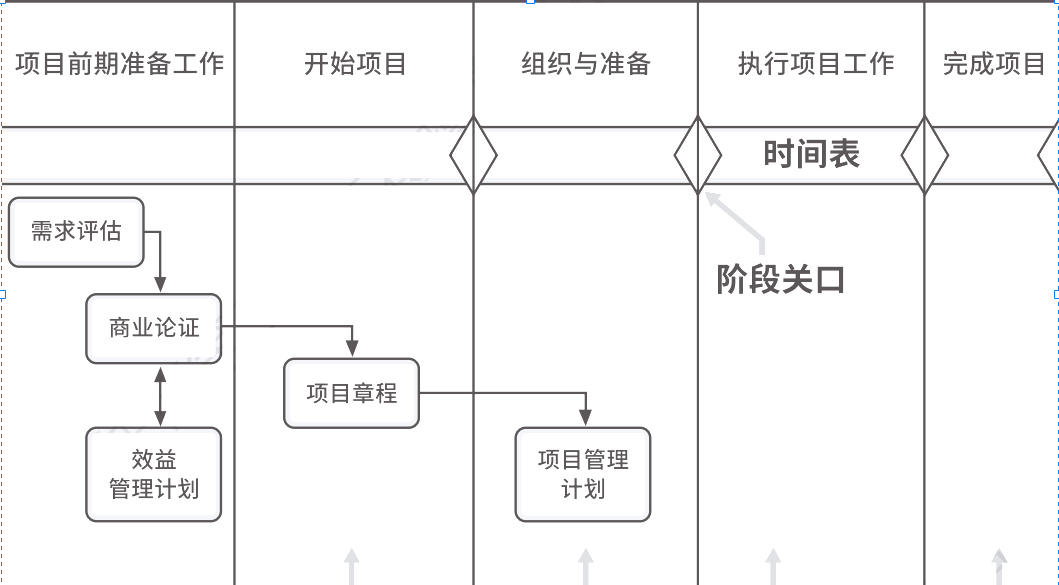
项目管理商业文件--商业论证与效益管理计划
本文描述从事项目管理和了解项目管理领域所需的基本知识,词汇定义来自于《项目知识管理体系》(PMBOK指南)第六版,仅作个人学习使用,任何对此文章的引用,应当说明源出处,不得用于商业用途。 如有侵权、联系速删 文章目录…...

机器学习揭秘:解锁从理论到实践的每一步!
机器学习揭秘:解锁从理论到实践的每一步! 机器学习:从理论到实践的完整指南引言第一部分:机器学习概念定义与重要性历史背景 第二部分:机器学习步骤数据收集数据预处理特征工程模型选择训练模型模型评估参数调优模型部…...
Kotlin协程CoroutineScope命名空间CoroutineName,Kotlin
Kotlin协程CoroutineScope命名空间CoroutineName,Kotlin import kotlinx.coroutines.*fun main(args: Array<String>) {val myName CoroutineName("fly")runBlocking {CoroutineScope(Dispatchers.IO).launch {repeat(3) {val name coroutineCont…...

HAL STM32G4 +TIM1 3路PWM互补输出+VOFA波形演示
HAL STM32G4 TIM1 3路PWM互补输出VOFA波形演示 ✨最近学习研究无刷电机驱动,虽然之前有使用过,但是在STM32上还没实现过。本文内容参考欧拉电子例程,从PWM驱动开始学习。 欧拉电子相关视频讲解: STM32G4 FOC开发实战—高级定时器发…...

MySQL进阶-----索引的结构与分类
目录 前言 一、认识索引 二、索引结构 1.概述 2. 二叉树 3 .B-Tree 4.BTree 5.Hash 三、索引的分类 1 .索引分类 2 .聚集索引&二级索引 前言 索引(index)是帮助MySQL高效获取数据的数据结构(有序)。在数据之外,数据库系统还维…...

FPGA高端项目:解码索尼IMX390 MIPI相机转HDMI输出,提供FPGA开发板+2套工程源码+技术支持
目录 1、前言2、相关方案推荐本博主所有FPGA工程项目-->汇总目录我这里已有的 MIPI 编解码方案 3、本 MIPI CSI-RX IP 介绍4、个人 FPGA高端图像处理开发板简介5、详细设计方案设计原理框图IMX390 及其配置MIPI CSI RX图像 ISP 处理图像缓存HDMI输出工程源码架构 6、工程源码…...

激光显示技术不断进步 国家政策推动行业发展
激光显示技术不断进步 国家政策推动行业发展 激光显示技术即用激光器作为光源的图像信息终端显示技术,是一种新型的投影显示技术。激光显示具有高亮度、色域覆盖率广、维护成本低等优点,在车载显示、家庭娱乐、教育等领域中应用广泛。激光显示产品主要有…...
iOS开发优势解析,费用探究以及软件开发详解
摘要 本文探讨了iOS开发的优势、费用以及软件开发方面的相关内容。通过分析iOS开发所采用的编程语言、开发环境、用户界面设计、应用审核流程以及应用领域等方面,展示了iOS开发的诸多优势和特点。虽然iOS开发具有高用户体验、统一的硬件和软件环境、良好的市场份额…...

02课程发布模块之部署Nginx
部署Nginx 部署网关 通过Nginx访问后台网关,然后由网关再将请求转发到具体的微服务,网关会把请求转发到具体的服务 upstream gatewayserver{server 127.0.0.1:63010 weight10; } # 网站首页对应的虚拟机 server {listen 80;server_name www.51xuecheng.cn…...
)
web学习笔记(四十二)
目录 1.ECMAScript 新特性-async 和await 1.1async函数 1.2await函数 1.3补充: 2. ES6模块化 2.1模块化的优点 2.2 ES6 模块化语法 2.3 ES6 模块暴露 2.4ES6 模块导入 1.ECMAScript 新特性-async 和await 1.1async函数 async函数可以单数使用,…...

大模型分布式推理ray
一、目录 1 框架 2. 入门 3. 安装教程 4. 相关文档、案例阅读 二、实现 1 框架:Ray:将一个模型拆分到多个显卡中,实现分布式预测、训练等功能。 2. 入门 : 案例:通过ray 实现分布式部署,分布式推理服务。…...

Python学习:循环语句
Python循环语句 概念 循环语句是编程中常用的结构,用于多次执行相同或类似的代码块。Python中有两种主要的循环语句:for循环和while循环。 for循环: for循环用于遍历一个序列(如列表、元组、字符串等)中的元素&#x…...

【物联网开源平台】tingsboard二次开发
别看这篇了,这篇就当我的一个记录,我有空我再写过一篇,编译的时候出现了一个错误,然后我针对那一个错误执行了一个命令,出现了绿色的succes,我就以为整个tingsboard项目编译成功了,后面发现的时候ÿ…...

Vue+ELement UI el-table移入或选中某行时改变颜色
起因 出库按钮 置灰时,鼠标移入到表格的某行时,行背景颜色与按钮背景颜色会被覆盖住 最初颜色 实现效果 修改行背景颜色 <style>/* 用来设置当前页面element全局table 选中某行时的背景色*/.el-table__body tr.current-row>td{background-c…...
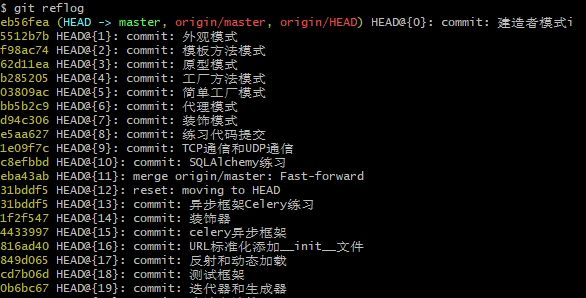
【Git】日志功能
1. git日志显示 # 显示前3条日志 git log -3# 单行显示 git log --oneline# 图表日志 git log --graph# 显示更改摘要 git log --stat# 显示更改位置 git log --patch 或 git log -p# 查看指定文件的提交历史记录 git log {filename}例子1:单行显示 例子2ÿ…...

【网络爬虫】(1) 网络请求,urllib库介绍
各位同学好,今天开始和各位分享一下python网络爬虫技巧,从基本的函数开始,到项目实战。那我们开始吧。 1. 基本概念 这里简单介绍一下后续学习中需要掌握的概念。 (1)http 和 https 协议。http是超文本传输…...
yolov9目标检测可视化图形界面GUI源码
该系统是由微智启软件工作室基于yolov9pyside6开发的目标检测可视化界面系统 运行环境: window python3.8 安装依赖后,运行源码目录下的wzq.py启动 程序提供了ui源文件,可以拖动到Qt编辑器修改样式,然后通过pyside6把ui转成python…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...

stm32wle5 lpuart DMA数据不接收
配置波特率9600时,需要使用外部低速晶振...

热门Chrome扩展程序存在明文传输风险,用户隐私安全受威胁
赛门铁克威胁猎手团队最新报告披露,数款拥有数百万活跃用户的Chrome扩展程序正在通过未加密的HTTP连接静默泄露用户敏感数据,严重威胁用户隐私安全。 知名扩展程序存在明文传输风险 尽管宣称提供安全浏览、数据分析或便捷界面等功能,但SEMR…...
