数据结构——lesson11排序之快速排序
💞💞 前言
hello hello~ ,这里是大耳朵土土垚~💖💖 ,欢迎大家点赞🥳🥳关注💥💥收藏🌹🌹🌹
💥个人主页:大耳朵土土垚的博客
💥 所属专栏:数据结构学习笔记 、排序算法合集
💥对于数据结构顺序表、链表、堆以及排序有疑问的都可以在上面数据结构专栏和排序合集专栏进行学习哦~ 有问题可以写在评论区或者私信我哦~
前面我们学习过五种排序——直接插入排序、希尔排序、直接选择排序、堆排序和冒泡排序,今天我们就来学习交换排序的第二种——快速排序。
1.快速排序(递归版)
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法,其基本思想为:任取待排序元素序列中的某元素作为基准值key,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复(这里使用递归来重复,非递归版本将在后续讲解)该过程,直到所有元素都排列在相应位置上为止。
那怎么实现左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值呢?
下面将介绍三个方法实现,分别是Hoare版本实现、挖坑法和前后指针法;
1.1Hoare版本实现
①选定一个基准值key(假设每次都为最左边的数),定义左右下标left,right;
②right先走从右往左找到小于key的值停在那里;
③左边再开始从左往右走直到停在大于key的值上,然后交换左右两个值;
④接着右边继续往左走继续找小于key的值,找到后左边往右走找大于key的值;
⑤直到左右left和right相遇,也就是left = right,此时该位置的值一定小于key(等学完Hoare后再来分析),再将该值与key交换即可;
🥳🥳这样key左边都是小于它的,右边都是大于它的,在整个序列中的位置就确定好了,接下来我们按照上述方法分别实现key左边的序列和右边的序列有序即可;
图示如下:
// 快速排序递归实现
// 快速排序hoare版本
int PartSort1(int* a, int left, int right)
{if (left >= right)//如果left一开始就小于right就不需要继续往下了return 0;int keyi = left;int key = a[left];while (left < right){//right先走while(left < right && a[right] < key ){if (a[left] > key){Swap(&a[left], &a[right]);break;}left++;}right--;}//当left=right时此时一定a[left] < a[keyi],要交换Swap(&a[left], &a[keyi]);return left;
}
void QuickSort(int* a, int left, int right)
{if (left >= right)//递归结束条件return;int keyi = PartSort1(a, left, right);QuickSort(a, left, keyi-1);//递归左右序列QuickSort(a, keyi+1, right);
}结果如下:
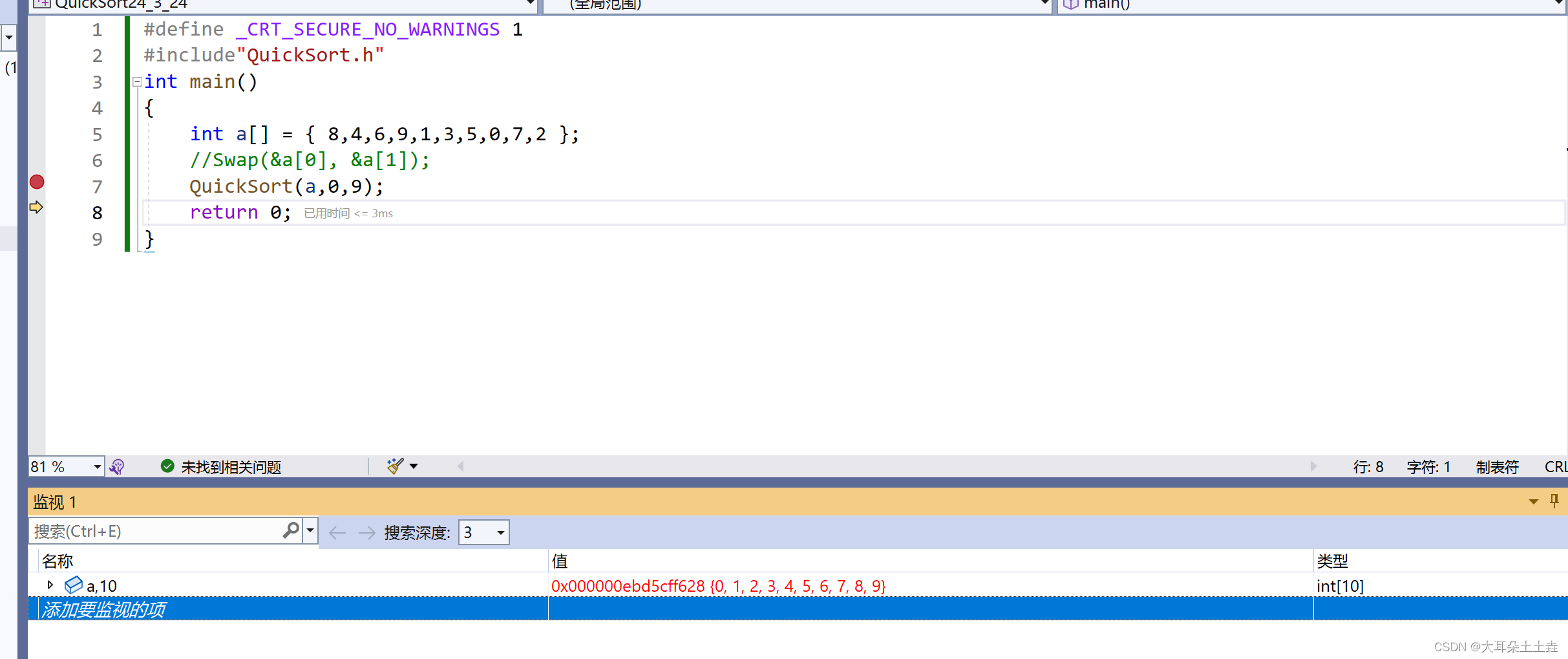
这里注意第二层while循环时也要讲条件left<right写上去,可以防止越界:当right首次向左走时如果没有一直遇到小于key的值那么right就有可能越界;
交换函数在这里🥳🥳
//交换函数
void Swap(int* a, int* b)
{int tmp = 0;tmp = *a;*a = *b;*b = tmp;
}
注意传指针才可以改变参数的值哦~
现在我们来分析为什么left = right时,该位置的值一定小于key
原因如下:
我们在看代码时发现是right先走,这肯定是有它的用意的
left与right相遇无非两种情况:
✨✨(1)left与right相遇:因为是right先走,所以left与right相遇,right此时肯定走过一次,right应该停在小于key的位置上,当left与right相遇时,此时该位置的值小于key
✨✨(2)right与left相遇:同样因为right先走,所以right与left相遇无非两种情况:
🧨🧨🧨①left一次都没走:此时right直接走到最左边,都不用管该位置值直接就是key,交换也没有影响所以可以不考虑;
🧨🧨🧨 ②left走了,那么当right走到与left相遇时,left的值是上次交换后小于key的值,所以相遇时该位置的值小于right;
所以如果将左边定位基准值key那么要让right先走:保障了相遇位置比key小;
依此类推:如果将右边定位基准值key,那么要让left先走:保障了相遇位置比key大;
1.2挖坑法实现
挖坑法较Hoare版本好理解:
①它先需要确定一个坑位hole和基准值key来存放坑位原来的值;
②左右下标也要有left和right,如果以左边的值为基准就要从右边先开始往左找到比key小的数填到坑位里,然后右边的就成为新的坑位;
(当然如果以右边的值为基准就要从左边开始往右找大于key的数)
③左边再开始找大于key的数,找到后填到新的坑位里,左边就成了新的坑位;
④依次循环直到left与right相遇跳出循环;
图示如下:
// 快速排序挖坑法
int PartSort2(int* a, int left, int right)
{int hole = left;int key = a[hole];while (left < right){//右边找小while (left < right && a[right] >= key){right--;}//填坑a[hole] = a[right];hole = right;//新坑//左边找大while (left < right && a[left] <= key){left++;}//填新坑a[hole] = a[left];hole = left;}//结束时坑位左边都比它小,右边都比它大a[hole] = key;return hole;}
//递归实现
void QuickSort(int* a, int left, int right)
{if (left >= right)//递归结束条件return;int keyi = PartSort2(a, left, right);QuickSort(a, left, keyi-1);//递归调用左边QuickSort(a, keyi+1, right);//递归调用右边}
注意✨✨:
①这里嵌套的while循环中也要写条件——left<right不然就会和Hoare版本一样出现越界访问;
②此外另外一个条件a[right] >= key,a[left] <= key不要漏掉等于号不然当左右两边都存在等于key的数时就会出现死循环哦~
结果如下:
1.3前后指针法实现💥
(1)前后指针法首先要定义指向数组的前后两个下标——prev和cur(注意这里的指针说的是下标),同时也需要基准值key(这里依然定义为最左边的数);
(2)这里的循环条件不太好实现:
✨①在没遇到小于key的值之前cur和prev一直向前;
✨②在遇到第一个大于key的值后,prev不再向前,因为prev开始时就时cur的前一位,所以此时prev的下一个就是第一个大于key的值;
✨③与此同时cur继续向前不做停顿,直到cur遇到小于key的值停下与++prev交换,这样一来之前遇到的大的值就被cur指向的小的值交换了,大的就到了后面;
✨④依此类推cur继续向后寻找小于key的值,prev同样不需要再向前,cur找到后与++prev交换…直到cur>right跳出循环;
(3)结束循环后prev的位置就是key合适的位置,交换两个位置的值并返回该位置的下标;
(4)然后再利用递归来实现完整序列的排序即可🥳🥳
图示如下:
// 快速排序前后指针法
int PartSort3(int* a, int left, int right)
{int key = a[left];int cur = left+1;int prev = left;while (cur <= right){//如果a[cur]<=key并且++prev的值不等于cur时说明prev与cur之间有大于key的值就需要交换了//如果a[cur]<=key并且++prev的值等于cur时说明此时还没出现大于key的值cur和prev继续向前//如果a[cur]>key说明出现了大的值,此时只要cur向前走就行,直到遇到下一个小值与++prev交换if (a[cur] <= key && ++prev != cur){Swap(&a[cur], &a[prev]);}cur++;}Swap(&a[prev], &a[left]);return prev;
}
//递归实现
void QuickSort(int* a, int left, int right)
{if (left >= right)//递归结束条件return;int keyi = PartSort3(a, left, right);QuickSort(a, left, keyi-1);//递归调用左边QuickSort(a, keyi+1, right);//递归调用右边}
结果如下:
如下图递归完一次之后int a[] = { 8,4,6,9,1,3,5,0,7,2 };最左边的数8找到了它最合适的位置——倒数第二位🥳🥳

排完序结果如下:

2.快速排序(非递归版)
快速排序的递归调用虽然能够解决问题,但是递归调用的是栈帧,是在栈上实现的,但是栈的空间一般只有8MB,如果递归很深的话有可能造成栈溢出的风险,所以我们也需要学习和掌握快速排序非递归版本;
要实现快速排序的非递归版本我们就可以用之前学习过的栈来模拟实现递归(当然使用队列也可以),详解在这里:数据结构——lesson5栈和队列;我们接下来将用到之前写过的栈来实现快速排序;
①我们利用栈先进后出的特点将左右子序列按照左右下标入栈的方式来标记,每次取出栈顶的元素当作左右下标;
②利用前面实现的三种方法任意一种来对序列进行排序;
③排好后获得key正确位置的下标keyi,并由keyi分割出两个左右子序列;
④并将两个序列的左右下标都入栈,等到下一次排序时调用;
⑤直到keyi无法分割时就不再继续入栈;
⑥直到栈空,排序也就完成🥳🥳
#include"stack.h"
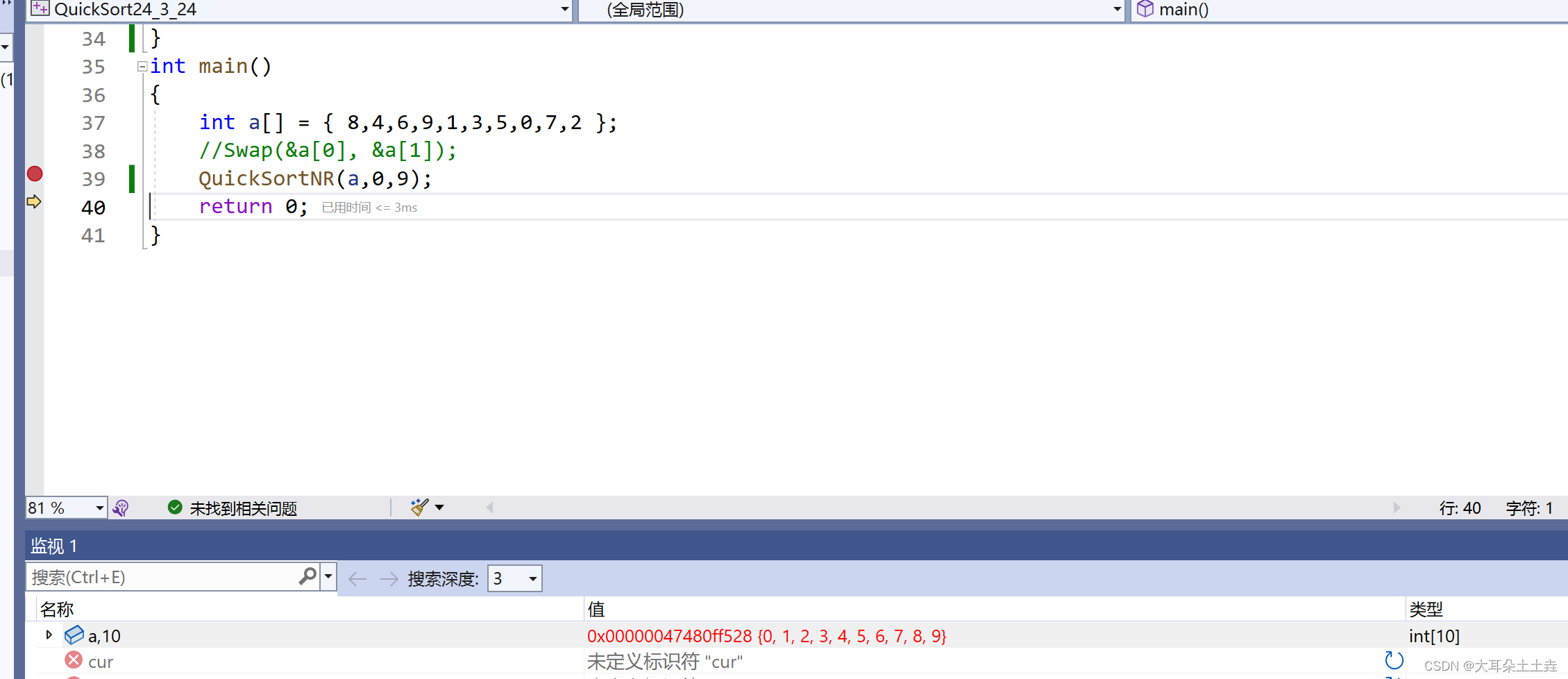
void QuickSortNR(int* a,int left,int right)
{//定义和初始化栈Stack ST;StackInit(&ST);//将整个序列入栈StackPush(&ST, right);StackPush(&ST, left);//当栈不为空时while (!StackEmpty(&ST)){//取栈顶的两个元素作为左右下标int left = StackTop(&ST);StackPop(&ST);int right = StackTop(&ST);StackPop(&ST);//利用前面讲过的三种方法任意一种来对取出的左右下标组成的序列排序int keyi = PartSort1(a, left, right);//如果能够分割左右序列就让它们入栈if (keyi + 1 < right){//记得入栈顺序不能随意,因为栈是先进后出有顺序要求StackPush(&ST, right);StackPush(&ST, keyi + 1);}if(left < keyi-1){//这里入栈顺序也要注意顺序StackPush(&ST, keyi - 1);StackPush(&ST, left);}}//销毁栈StackDestroy(&ST);}
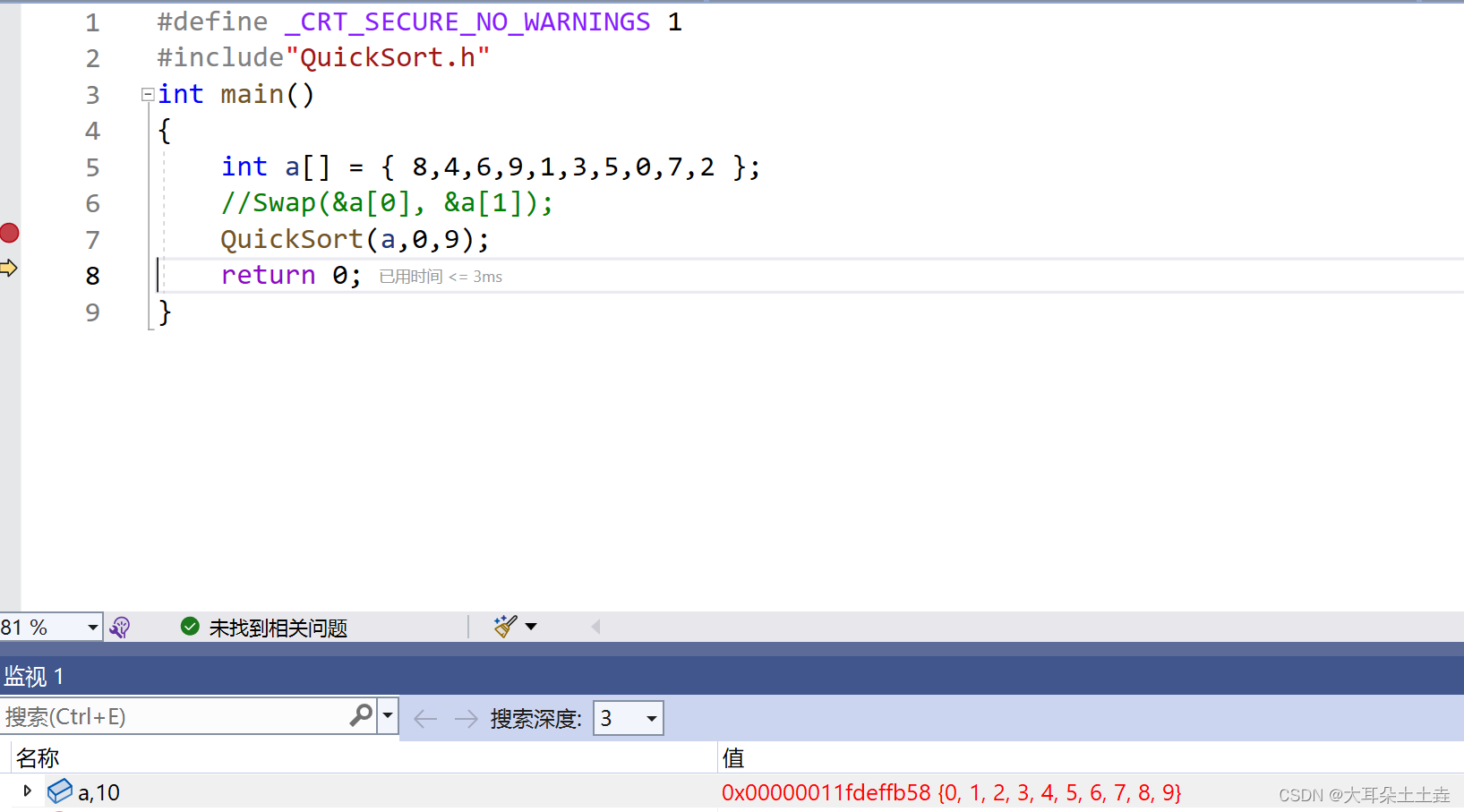
int main()
{int a[] = { 8,4,6,9,1,3,5,0,7,2 };//Swap(&a[0], &a[1]);QuickSortNR(a,0,9);return 0;
}
结果如下:
3.快速排序(改良版)
我们发现如果序列在接近有序的情况下,快速排序都会非常的慢,因为我们每次PartSort取得都是最左边的元素作为基准值key,如果在接近有序的情况下要遍历N遍数组,数组序列每次-1,类似于等差数列,效率太低;如下图所示:
此时时间复杂度为O(N^2);
🥳🥳所以我们可以选择一个不那么大或者不那么小的元素作为基准值key,这样就可以提高快速排序的效率啦~
我们使用三书取中的方法,也就是取左、右、中间三个元素进行比较,取不大也不小的数作为基准值即可;
代码如下:
int GetMidIndex(int* a, int left, int right)
{int mid = (left + right) / 2;if (a[left] < a[mid]){if (a[mid] < a[right]){return mid;}else if (a[left] < a[right]){return right;}else{return left;}}else // a[left] > a[mid]{if (a[mid] > a[right]){return mid;}else if (a[left] > a[right]){return right;}else{return left;}}
}获得中间值的下标后直接与最左边的数交换即可(以Hoare版本为例):
// 快速排序递归实现
// 快速排序hoare版本
int PartSort1(int* a, int left, int right)
{if (left >= right)//如果left一开始就小于right就不需要继续往下了return 0;int midi = GetMidIndex(a,left,right);//与left的值交换即可,其他不变Swap(&a[left],&a[midi]);int keyi = left;int key = a[left];while (left < right){//right先走while(left < right && a[right] < key ){if (a[left] > key){Swap(&a[left], &a[right]);break;}left++;}right--;}//当left=right时此时一定a[left] < a[keyi],要交换Swap(&a[left], &a[keyi]);return left;
}
void QuickSort(int* a, int left, int right)
{if (left >= right)//递归结束条件return;int keyi = PartSort1(a, left, right);QuickSort(a, left, keyi-1);//递归左右序列QuickSort(a, keyi+1, right);
}其他两种方法和上述一致🥳🥳🥳
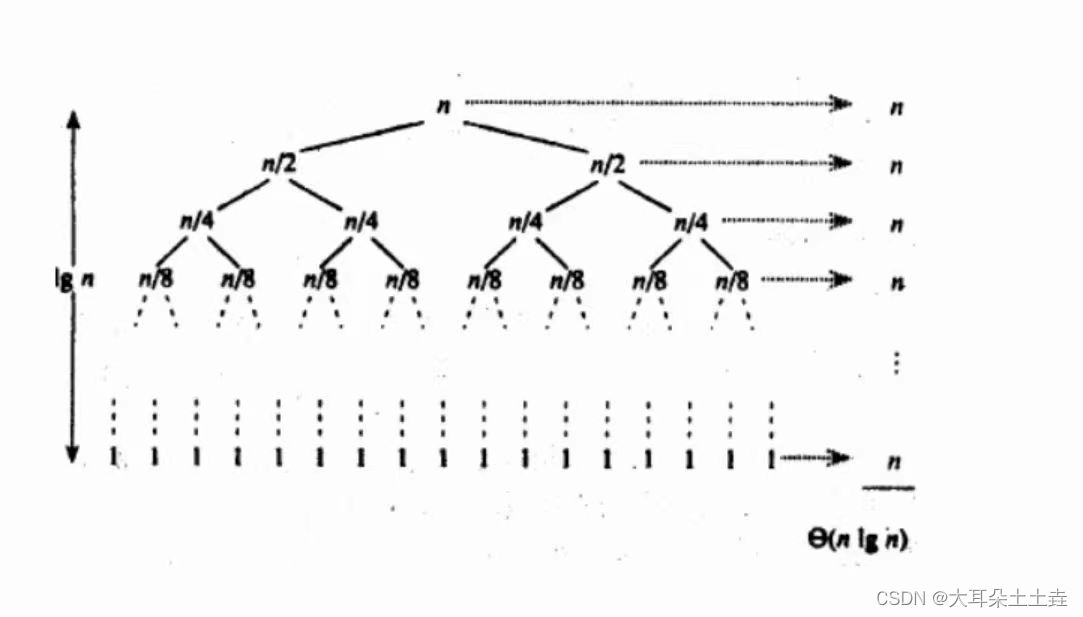
4.快速排序复杂度分析
4.1快速排序空间复杂度
无论时递归还是非递归实现,调用的空间都是O(logN),递归实现要调用栈帧,左右子序列,类似于二分,左序列再调用左右序列…,并且空间是可以复用的,左边归还之后调用右边序列则可以重复使用,所以调用的空间是logN(以2为底);
非递归实现使用了栈,与递归过程类似;
4.2快速排序时间复杂度
快排改良版的时间复杂度是:O(NlogN)
此时不需要遍历N遍,只需要logN层即可遍历完,每层都是N次,所以是O(NlogN);
5.结语
以上就是快速排序的所有内容啦~我们共使用了递归版的三种方法以及非递归版来实现快速排序,并改良了快速排序,分析了它的时间和空间复杂度,完结撒花 ~🥳🥳🎉🎉🎉
相关文章:
数据结构——lesson11排序之快速排序
💞💞 前言 hello hello~ ,这里是大耳朵土土垚~💖💖 ,欢迎大家点赞🥳🥳关注💥💥收藏🌹🌹🌹 💥个人主页&#x…...

Nacos部署(二)Linux部署Nacos2.3.x集群环境
😊 作者: 一恍过去 💖 主页: https://blog.csdn.net/zhuocailing3390 🎊 社区: Java技术栈交流 🎉 主题: Nacos部署(二)Linux部署Nacos2.3.x集群环境 ⏱️…...

RuoYi 自定义字典列表页面编码翻译
“字典数据”单独维护,而不是使用系统自带的字典表,应该如何使用这样的字典信息呢? 系统字典的使用,请参考: 《RuoYi列表页面字典翻译的实现》 https://blog.csdn.net/lxyoucan/article/details/136877238 需求说明…...
GAMES101 学习4
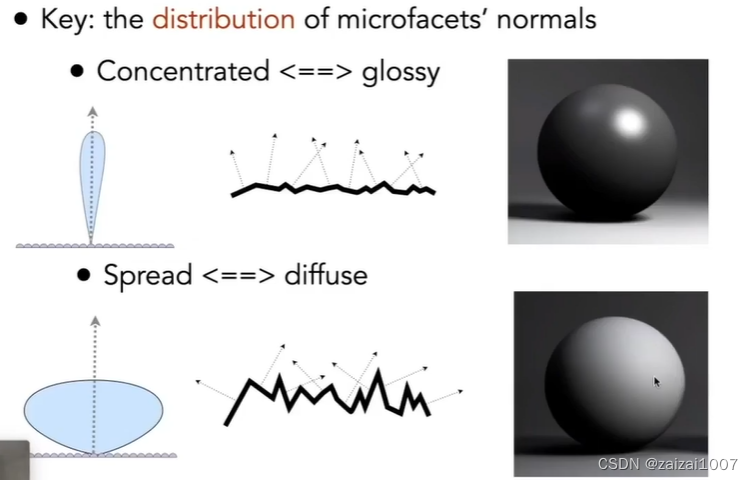
材质和外观 材质 BRDF 漫反射 任何方向的光进来都会被均匀的反射到周围各个不同的方向上去 假设能量守恒,那么 Li Lo,这之后BRDF就 ,就可以定义一个反照率 (Albeo) - ,在(0 - 1࿰…...
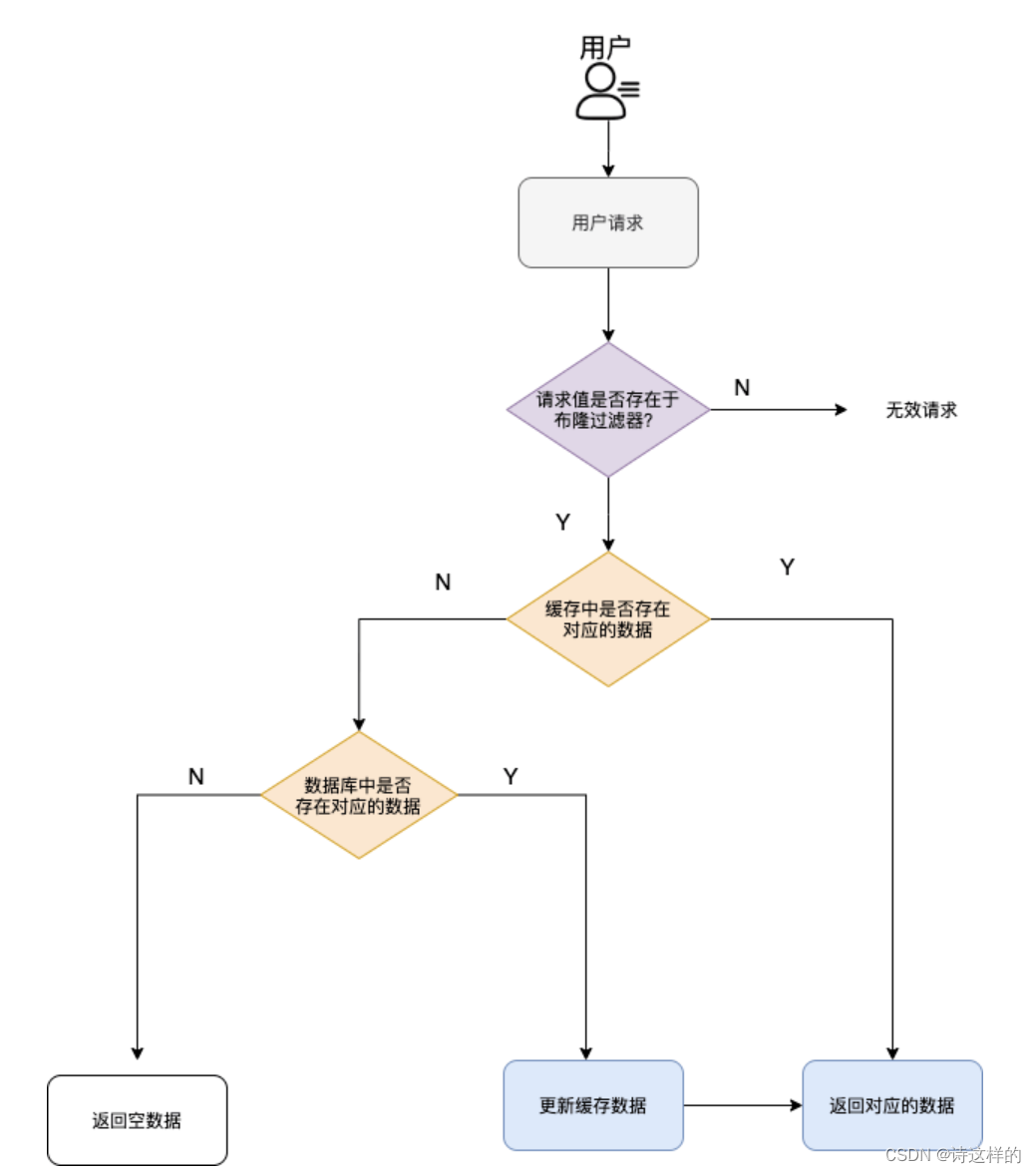
Redis中的缓存穿透
缓存穿透 缓存穿透是指客户端请求的数据在缓存中和数据库中都不存在,导致这些请求直接到了数据库上,对数据库造成了巨大的压力,可能造成数据库宕机。 常见的解决方案: 1)缓存无效 key 如果缓存和数据库中都查不到某…...
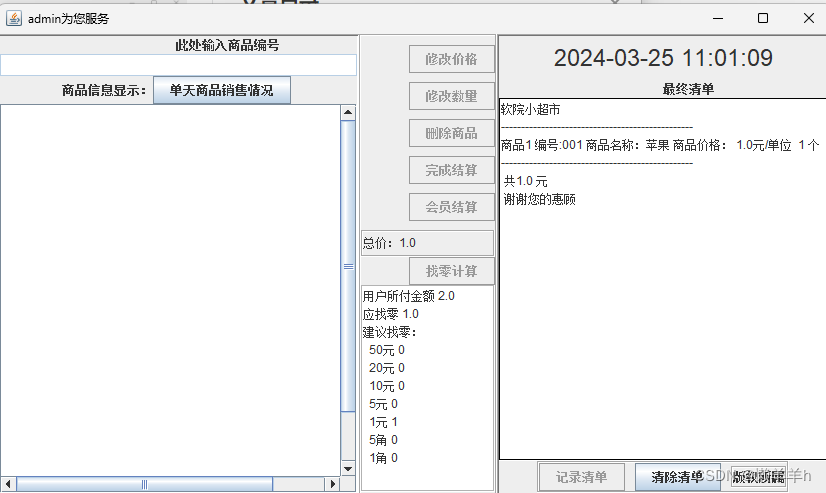
javaSwing超市收银(txt)
一、简介 超市收银系统是商店管理的重要组成部分,它可以帮助商家高效地进行商品管理、销售记录和结算。本文将介绍如何使用Java Swing开发一个简单的超市收银系统,包括基本功能如登录、修改商品信息、结算等,并利用txt文本作为数据库存储商品…...

Linux 理解文件系统、磁盘结构、软硬链接
目录 一、理解磁盘结构 1、磁盘的物理结构 2、硬件层面理解 3、磁盘的具体物理存储结构 4、进行逻辑抽象 5、磁盘文件的管理 6、创建新文件的过程 二、理解文件系统 1、文件的构成 2、为何选择4KB而非512字节作为基本单位? 3、文件系统的组成 数据块(Data Blocks&a…...

智慧商场数字化创新需要有数字能力帮手
商场和商圈是是促进流通创新、培育新兴消费的载体。很多实体店为适应消费升级需求新变化,加快运用现代信息技术,建设智慧商店,创新消费场景。蚓链运用现代信息技术(互联网、物联网、5G、大数据、人工智能、云计算等)&a…...

JS加密解密之应用如何保存到桌面书签
前言 事情起因是这样的,有个客户解密了一个js,然后又看不懂里边的一些逻辑,想知道它是如何自动拉起谷歌浏览器和如何保存应用到书签的,以及如何下载应用的。继而诞生了这篇文章,讲解一下他的基本原理。 渐进式Web应用…...

线上linux服务器升级nginx
一个nginx版本空包 一个pcre文件 一个zlib文件 ./configure配置文件 make编译 make install复制所有文件到nginx 如果nginx -v无版本号 检查环境变量cat /etc/profile 编辑 环境变量vi /etc/profile 按i进入编辑模式 按esc进入查看模式 因为path中并未使用%JAVA_HOME%字样…...

使用JDK提供的常用工具在多线程编写线程安全和数据同步的程序
题图来自APOD 你好,这里是codetrend专栏“高并发编程基础”。 引言 在并发执行任务时,由于资源共享的存在,线程安全成为一个需要考虑的问题。与串行化程序相比,并发执行可以更好地利用CPU计算能力,提高系统的吞吐量…...

八道Python入门级题目及答案详解
前言 介绍Python作为一门流行的编程语言,易学易用的特点。强调通过练习题目来加深对Python语法和编程概念的理解。 题目一:计算两个数的和 描述:编写一个Python程序,计算两个数的和,并输出结果。举例:输…...

Git 的cherry-pick含义
目录 1. cherry-pick的基本概念 2. cherry-pick的使用场景 3. cherry-pick的使用方法 结论 1. cherry-pick的基本概念 git cherry-pick是一个Git命令,它允许你选择一个或多个其他分支上的提交(commits),并将它们复制到你当前的…...

大数据中TopK问题
1.给定100个int数字,在其中找出最大的10个; import java.util.PriorityQueue;public class Main {public static void main(String[] args) {final int topK 3;int[] vec {4, 1, 5, 8, 7, 2, 3, 0, 6, 9};PriorityQueue<Integer> pq new PriorityQueue<…...

基于SpringBoot+MyBatis+Vue的电商智慧仓储管理系统的设计与实现(源码+LW+部署+讲解)
前言 博主简介👨🏼⚕️:国内某一线互联网公司全栈工程师👨🏼💻,业余自媒体创作者💻,CSDN博客专家🏆,Java领域优质创作者📕&#x…...
)
C++经典面试题目(四)
1、请解释const关键字的作用。 在C中,const关键字主要用来表示“不变性”,即被它修饰的东西是不可修改的。它可以用于多种上下文: 修饰基本数据类型变量:声明一个常量,一旦初始化后,其值就不能再更改。 co…...

2024/3/24 蓝桥杯
P1678 烦恼的高考志愿 二分 import java.util.Arrays; import java.util.Scanner;public class Main {public static void main(String[] args) {Scanner sc new Scanner(System.in);int n sc.nextInt();int m sc.nextInt();int[] a new int[n1];//学校int[] b new int[m…...

用户验证:Streamlit应用程序与Streamlit-Authenticator
写在前面 在数字化时代,数据安全和用户隐私越来越受到重视。对于使用Streamlit构建的Web应用程序来说,确保用户的安全身份验证是至关重要的。而Streamlit-Authenticator,作为一个专门为Streamlit应用程序设计的身份验证库,正成为保…...
风丘EV能量流测试解决方案 提高电动汽车续航能力
电动汽车(EV)近些年发展迅猛,已被汽车业内普遍认为是未来汽车发展的新方向,但现如今电动汽车仍然存在一些短板,导致其还无法替代传统燃油车。对此,首先想到的肯定就是电动车的续航问题。其实解决电动车续航…...

【Python】输出一个 Python 项目下需要哪些第三方包
方法一 pycharm 方法二 要分析一个 Python 项目下需要哪些第三方包并生成 requirements.txt 文件,你可以使用 pipreqs 工具。以下是具体的步骤: 首先,确保你已经安装了 pipreqs 工具。如果未安装,可以使用以下命令进行安装&a…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...

TJCTF 2025
还以为是天津的。这个比较容易,虽然绕了点弯,可还是把CP AK了,不过我会的别人也会,还是没啥名次。记录一下吧。 Crypto bacon-bits with open(flag.txt) as f: flag f.read().strip() with open(text.txt) as t: text t.read…...