【字符串】字符串哈希
因为习惯了STL,所以一直没有接触这块儿的内容,今天cf碰到学着用了一下发现还蛮好用的
单哈希
字符串哈希 简单来说就是把一个字符串对应到一个数上,且一个字符串唯一对应一个数,一个数也唯一对应一个字符串
怎么进行这个操作呢?
我们定义一个 base 和一个 mod
字符串 s 1 s 2 s 3 s_1s_2s_3 s1s2s3 就可以表示为 ( s 1 − ′ a ′ ) × b a s e 2 + ( s 2 − ′ a ′ ) × b a s e 1 + ( s 3 − ′ a ′ ) × b a s e 0 (s_1 - 'a')\times base^2+(s_2 - 'a')\times base^1+(s_3 - 'a')\times base^0 (s1−′a′)×base2+(s2−′a′)×base1+(s3−′a′)×base0 (未取模的结果)
base 一般取值 131 1331 13331 (以此类推)
mod 建议取一些奇奇怪怪的值,比如说 1e13+39
通过这个操作把字符串转换成数,之后判断两个字符串是否相等,只需要判断两个数是否相等就可以了
双哈希
虽然经过上面的操作,不同的字符串对应同一个数的概率已经非常小了,但是还是有这个可能性的,所以为了把出错的概率继续降低,我们可以使用双哈希
定义 mod1 mod2 ,让每个字符串对应两个数,只有当两个字符串产生的两个数完全一致时,才判定这两个字符串相等。(依此类推,还可以进行更多次数的哈希降低出错概率)
板子
预处理base的次方
p[0] = 1;
for (int i = 1; i < N; i ++ ) p[i] = p[i - 1] * base % mod1;
将字符串转换成数
int hash_cal(string s)
{int res = 0;for (int i = 0; i < s.size(); i ++ )res = (res * base % mod1 + s[i] - 'a') % mod1;return res;
}
查询
for (int i = 0; i < n; i ++ )
{string s;cin >> s;hash_set[i] = hash_cal(s);
}
sort(hash_set, hash_set + n);
for (int i = 0; i < m; i ++ )
{string s;cin >> s;int tmp = hash_cal(s);if (*lower_bound(hash_set, hash_set + n, tmp) == tmp) cout << "YES\n";else cout << "NO\n";
}
相关文章:

【字符串】字符串哈希
因为习惯了STL,所以一直没有接触这块儿的内容,今天cf碰到学着用了一下发现还蛮好用的 单哈希 字符串哈希 简单来说就是把一个字符串对应到一个数上,且一个字符串唯一对应一个数,一个数也唯一对应一个字符串 怎么进行这个操作呢…...

MacOS快速安装FFmpeg、ffprobe、ffplay
文章目录 一、工具简介二、mac 安装ffprobe、FFmpeg等相关工具2.1 方法一:使用Homebrew安装FFmpeg2.2 从官网下载FFmpeg安装包,源码安装2.3 macOS 无法验证开发者时安装 一、工具简介 这些工具都是与多媒体处理和流媒体相关的开源工具,它们都…...
数据结构 之 树习题 力扣oj(附加思路版)
层序遍历 算法流程: 1.创建一个队列记为que,将根节点放入队列。 2.每次从队列中弹出一个节点,记为node。 3.第三步看这个node有没有左孩子,如果有左孩子把左孩子放入到队列中,如果node有右孩子,把右孩子放入到队列中。…...

闭包学习,闭包和高阶函数
面试官反复在前端面试中提出闭包相关的问题,并要求提供代码示例,主要是为了考察以下几点: 1.概念:考察候选人是否真正理解闭包是如何形成的,即当一个函数可以访问并操作其外部作用域中的变量,即使在其外部…...
 shell)
Linux实战笔记(五) shell
大家好,我是半虹,这篇文章我们介绍一下 shell 1、Shell Shell 通常泛指系统提供给用户的操作界面,是系统内核与用户之间的连接 Shell 这个名字其实还挺形象的,中文翻译是壳,什么的壳呢,自然是系统内核的壳…...

TCP Wrappers 的使用
以ssh为例,每当有ssh的连接请求时,先读取系统管理员所设置的访问控制文件,符合要求,则会把这次连接原封不 动的转给ssh进程,由ssh完成后续工作;如果这次连接发起的ip不符合访问控制文件中的设置,…...
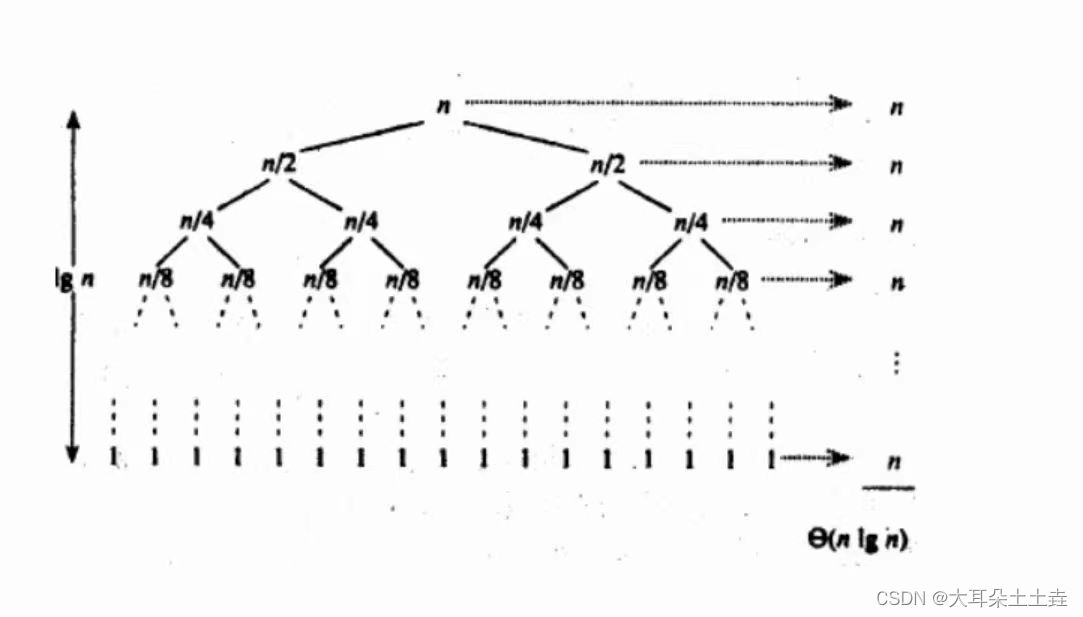
数据结构——lesson11排序之快速排序
💞💞 前言 hello hello~ ,这里是大耳朵土土垚~💖💖 ,欢迎大家点赞🥳🥳关注💥💥收藏🌹🌹🌹 💥个人主页&#x…...

Nacos部署(二)Linux部署Nacos2.3.x集群环境
😊 作者: 一恍过去 💖 主页: https://blog.csdn.net/zhuocailing3390 🎊 社区: Java技术栈交流 🎉 主题: Nacos部署(二)Linux部署Nacos2.3.x集群环境 ⏱️…...

RuoYi 自定义字典列表页面编码翻译
“字典数据”单独维护,而不是使用系统自带的字典表,应该如何使用这样的字典信息呢? 系统字典的使用,请参考: 《RuoYi列表页面字典翻译的实现》 https://blog.csdn.net/lxyoucan/article/details/136877238 需求说明…...
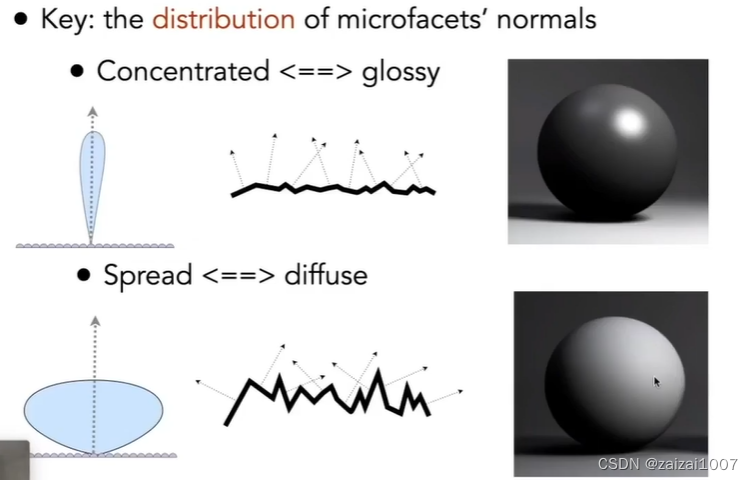
GAMES101 学习4
材质和外观 材质 BRDF 漫反射 任何方向的光进来都会被均匀的反射到周围各个不同的方向上去 假设能量守恒,那么 Li Lo,这之后BRDF就 ,就可以定义一个反照率 (Albeo) - ,在(0 - 1࿰…...
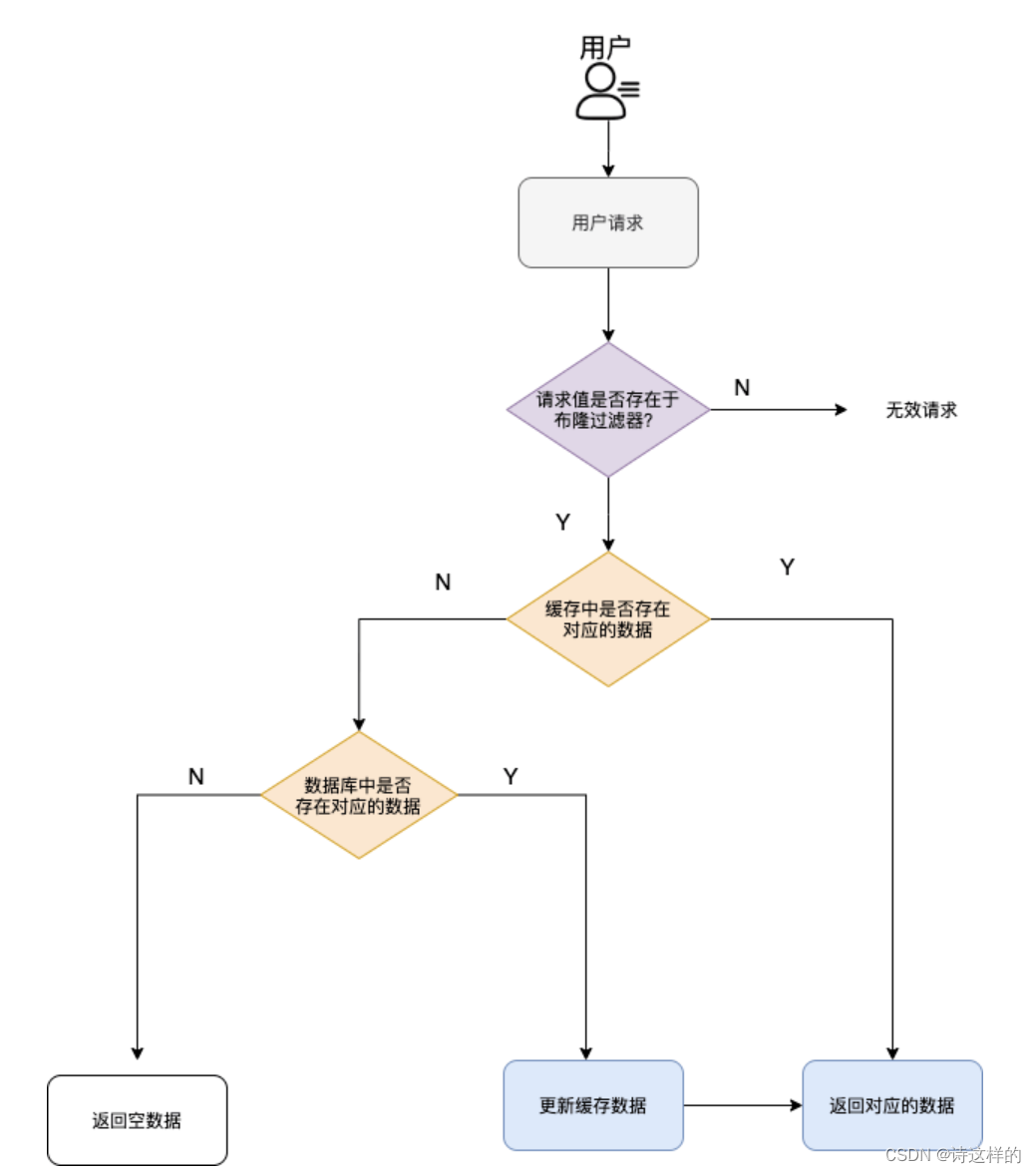
Redis中的缓存穿透
缓存穿透 缓存穿透是指客户端请求的数据在缓存中和数据库中都不存在,导致这些请求直接到了数据库上,对数据库造成了巨大的压力,可能造成数据库宕机。 常见的解决方案: 1)缓存无效 key 如果缓存和数据库中都查不到某…...
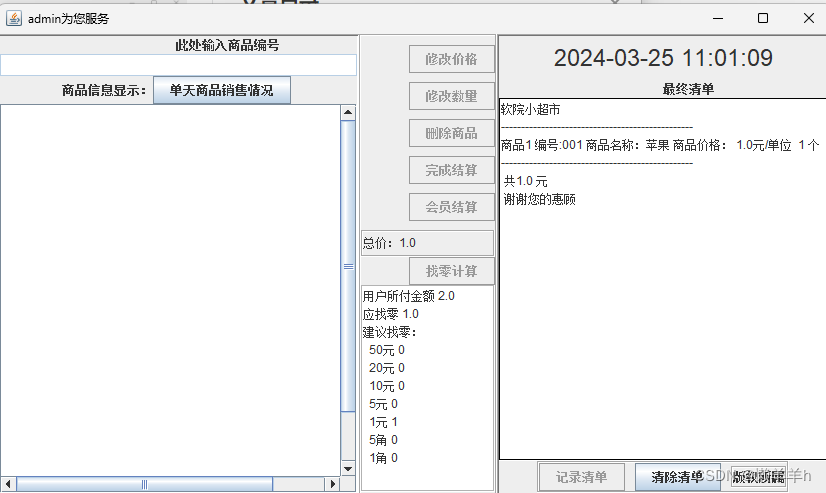
javaSwing超市收银(txt)
一、简介 超市收银系统是商店管理的重要组成部分,它可以帮助商家高效地进行商品管理、销售记录和结算。本文将介绍如何使用Java Swing开发一个简单的超市收银系统,包括基本功能如登录、修改商品信息、结算等,并利用txt文本作为数据库存储商品…...

Linux 理解文件系统、磁盘结构、软硬链接
目录 一、理解磁盘结构 1、磁盘的物理结构 2、硬件层面理解 3、磁盘的具体物理存储结构 4、进行逻辑抽象 5、磁盘文件的管理 6、创建新文件的过程 二、理解文件系统 1、文件的构成 2、为何选择4KB而非512字节作为基本单位? 3、文件系统的组成 数据块(Data Blocks&a…...

智慧商场数字化创新需要有数字能力帮手
商场和商圈是是促进流通创新、培育新兴消费的载体。很多实体店为适应消费升级需求新变化,加快运用现代信息技术,建设智慧商店,创新消费场景。蚓链运用现代信息技术(互联网、物联网、5G、大数据、人工智能、云计算等)&a…...

JS加密解密之应用如何保存到桌面书签
前言 事情起因是这样的,有个客户解密了一个js,然后又看不懂里边的一些逻辑,想知道它是如何自动拉起谷歌浏览器和如何保存应用到书签的,以及如何下载应用的。继而诞生了这篇文章,讲解一下他的基本原理。 渐进式Web应用…...

线上linux服务器升级nginx
一个nginx版本空包 一个pcre文件 一个zlib文件 ./configure配置文件 make编译 make install复制所有文件到nginx 如果nginx -v无版本号 检查环境变量cat /etc/profile 编辑 环境变量vi /etc/profile 按i进入编辑模式 按esc进入查看模式 因为path中并未使用%JAVA_HOME%字样…...

使用JDK提供的常用工具在多线程编写线程安全和数据同步的程序
题图来自APOD 你好,这里是codetrend专栏“高并发编程基础”。 引言 在并发执行任务时,由于资源共享的存在,线程安全成为一个需要考虑的问题。与串行化程序相比,并发执行可以更好地利用CPU计算能力,提高系统的吞吐量…...

八道Python入门级题目及答案详解
前言 介绍Python作为一门流行的编程语言,易学易用的特点。强调通过练习题目来加深对Python语法和编程概念的理解。 题目一:计算两个数的和 描述:编写一个Python程序,计算两个数的和,并输出结果。举例:输…...

Git 的cherry-pick含义
目录 1. cherry-pick的基本概念 2. cherry-pick的使用场景 3. cherry-pick的使用方法 结论 1. cherry-pick的基本概念 git cherry-pick是一个Git命令,它允许你选择一个或多个其他分支上的提交(commits),并将它们复制到你当前的…...

大数据中TopK问题
1.给定100个int数字,在其中找出最大的10个; import java.util.PriorityQueue;public class Main {public static void main(String[] args) {final int topK 3;int[] vec {4, 1, 5, 8, 7, 2, 3, 0, 6, 9};PriorityQueue<Integer> pq new PriorityQueue<…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...
