0202矩阵的运算-矩阵及其运算-线性代数
文章目录
- 一、矩阵的加法
- 二、数与矩阵相乘
- 三、矩阵与矩阵相乘
- 四、矩阵的转置
- 五、方阵的行列式
- 结语
一、矩阵的加法
定义2 设有两个 m × n m\times n m×n橘子 A = ( a i j ) 和 B = ( b i j ) A=(a_{ij})和B=(b_{ij}) A=(aij)和B=(bij),那么矩阵A与B的和记为A+B,规定为
A + B = ( a 11 + b 11 a 12 + b 12 ⋯ a 1 n + b 1 n a 21 + b 21 a 22 + b 22 ⋯ a 2 n + b 2 n ⋮ ⋮ ⋮ a m 1 + b m 1 a m 2 + b m 2 ⋯ a m n + b m n ) A+B=\begin{pmatrix} a_{11}+b_{11}&a_{12}+b_{12}&\cdots&a_{1n}+b_{1n}\\ a_{21}+b_{21}&a_{22}+b_{22}&\cdots&a_{2n}+b_{2n}\\ \vdots&\vdots&&\vdots\\ a_{m1}+b_{m1}&a_{m2}+b_{m2}&\cdots&a_{mn}+b_{mn}\\ \end{pmatrix} A+B= a11+b11a21+b21⋮am1+bm1a12+b12a22+b22⋮am2+bm2⋯⋯⋯a1n+b1na2n+b2n⋮amn+bmn
**tips:**只有当两个矩阵是同型矩阵时,这两个矩阵才能进行加法运算。
矩阵加法满足下列运算规律(设A,B,C都是 m × n m\times n m×n矩阵):
- A + B = B + A A+B=B+A A+B=B+A
- ( A + B ) + C = A + ( B + C ) (A+B)+C=A+(B+C) (A+B)+C=A+(B+C)
设矩阵 A = ( a i j ) A=(a_{ij}) A=(aij),记
− A = ( − a i j ) -A=(-a_{ij}) −A=(−aij)
-A称为矩阵A的负矩阵,显示有
A + ( − A ) = O A+(-A)=O A+(−A)=O
矩阵的减法为
A − B = A + ( − B ) A-B=A+(-B) A−B=A+(−B)
二、数与矩阵相乘
定义3 数 λ \lambda λ与矩阵A的乘积记作 λ A 或 A λ \lambda A或A\lambda λA或Aλ,规定为
λ A = A λ = ( λ a 11 λ a 12 ⋯ λ a 1 n λ a 21 λ a 22 ⋯ λ a 2 n ⋮ ⋮ ⋮ λ a m 1 λ a m 2 ⋯ λ a m n ) \lambda A=A\lambda=\begin{pmatrix} \lambda a_{11}&\lambda a_{12}&\cdots&\lambda a_{1n}\\ \lambda a_{21}&\lambda a_{22}&\cdots&\lambda a_{2n}\\ \vdots&\vdots&&\vdots\\ \lambda a_{m1}&\lambda a_{m2}&\cdots&\lambda a_{mn}\\ \end{pmatrix} λA=Aλ= λa11λa21⋮λam1λa12λa22⋮λam2⋯⋯⋯λa1nλa2n⋮λamn
数乘矩阵满足下列运算规律(设A、B为 m × n m\times n m×n矩阵, λ 、 μ \lambda、\mu λ、μ为数):
- ( λ μ ) A = λ ( μ A ) (\lambda\mu)A=\lambda(\mu A) (λμ)A=λ(μA)
- ( λ + μ ) A = λ A + μ A (\lambda+\mu)A=\lambda A+\mu A (λ+μ)A=λA+μA
- λ ( A + B ) = λ A + λ B \lambda(A+B)=\lambda A+\lambda B λ(A+B)=λA+λB
矩阵加法和数乘矩阵统称为矩阵的线性运算。
三、矩阵与矩阵相乘
定义4 设 A = ( a i j ) 是一个 m × s A=(a_{ij})是一个m\times s A=(aij)是一个m×s的矩阵, B = ( b i j ) 是一个 s × n B=(b_{ij})是一个s\times n B=(bij)是一个s×n的矩阵,那么规定矩阵A与矩阵B的乘积是一个 m × n m\times n m×n矩阵 C = ( c i j ) C=(c_{ij}) C=(cij),其中
c i j = a i 1 b 1 j + a i 2 b 2 j + ⋯ + a i s b s j = ∑ k = 1 n a i k b j k , ( i = 1 , 2 , ⋯ , m ; j = 1 , 2 , ⋯ , n ) c_{ij}=a_{i1}b_{1j}+a_{i2}b_{2j}+\cdots+a_{is}b_{sj}=\sum_{k=1}^na_{ik}b_{jk},(i=1,2,\cdots,m;j=1,2,\cdots,n) cij=ai1b1j+ai2b2j+⋯+aisbsj=∑k=1naikbjk,(i=1,2,⋯,m;j=1,2,⋯,n)
并把此乘积记作
C = A B C=AB C=AB
说明:
- 乘积矩阵 A B = C 的 ( i , j ) 元 c i j AB=C的(i,j)元c_{ij} AB=C的(i,j)元cij就是A的第 i i i行和B的第 j j j列的乘积。
- 只有当第一个矩阵的(左矩阵)的列数等于第二个矩阵的(右矩阵)的行数时,两个矩阵才能相乘。
例5 求矩阵
A = ( 4 − 1 2 1 1 1 0 3 0 3 1 4 ) 与 B = ( 1 2 0 1 3 0 − 1 2 ) A=\begin{pmatrix} 4&-1&2&1\\ 1&1&0&3\\ 0&3&1&4\\ \end{pmatrix} 与B=\begin{pmatrix} 1&2\\ 0&1\\ 3&0\\ -1&2\\ \end{pmatrix} A= 410−113201134 与B= 103−12102
的乘积
C = A B = ( 4 + 0 + 6 − 1 8 − 1 + 0 + 2 1 + 0 + 0 − 3 2 + 1 + 0 + 6 0 + 0 + 3 − 4 0 + 3 + 0 + 8 ) = C = A B = ( 9 9 − 2 9 − 1 11 ) C=AB=\begin{pmatrix} 4+0+6-1&8-1+0+2\\ 1+0+0-3&2+1+0+6\\ 0+0+3-4&0+3+0+8\\ \end{pmatrix}\\ =C=AB=\begin{pmatrix} 9&9\\ -2&9\\ -1&11\\ \end{pmatrix} C=AB= 4+0+6−11+0+0−30+0+3−48−1+0+22+1+0+60+3+0+8 =C=AB= 9−2−19911
例6 求矩阵
A = ( − 2 4 1 − 2 ) 与 B = ( 2 4 − 3 − 6 ) A=\begin{pmatrix} -2&4\\ 1&-2 \end{pmatrix} 与B=\begin{pmatrix} 2&4\\ -3&-6 \end{pmatrix} A=(−214−2)与B=(2−34−6)
的乘积AB级BA
A B = ( − 16 − 32 8 16 ) B A = ( 0 0 0 0 ) AB=\begin{pmatrix} -16&-32\\ 8&16\\ \end{pmatrix}\\ BA=\begin{pmatrix} 0&0\\ 0&0\\ \end{pmatrix}\\ AB=(−168−3216)BA=(0000)
tips:
- A B AB AB有意思,但是 B A BA BA不一定有意义;若 B A BA BA有意义,但AB与BA不一定相等。
- 对于n阶方阵A、B,若AB=BA,则称方阵A与B可交换。
- 若两个矩阵A、B满足 A B = O AB=O AB=O,不能得出 A = O 或 B = O A=O或B=O A=O或B=O;若 A ≠ O A\not=O A=O而 A ( X − Y ) = O A(X-Y)=O A(X−Y)=O,不能得出 X = Y X=Y X=Y的结论。
矩阵的乘法虽不满足交换律,但仍满足下列结合律和分配律(假设运算都是可行的):
- ( A B ) C = A ( B C ) (AB)C=A(BC) (AB)C=A(BC)
- λ ( A B ) = ( λ A ) B = A ( λ B ) \lambda(AB)=(\lambda A)B=A(\lambda B) λ(AB)=(λA)B=A(λB)
- A ( B + C ) = A B + A C , ( B + C ) A = B A + C A A(B+C)=AB+AC,(B+C)A=BA+CA A(B+C)=AB+AC,(B+C)A=BA+CA
对于单位矩阵E,容易验证
E M A m × n = A m × n , A m × n E n = A m × n E_MA_{m\times n}=A_{m\times n},A_{m\times n}E_n=A_{m\times n} EMAm×n=Am×n,Am×nEn=Am×n
或简写EA=AE=A
矩阵
( λ λ ⋱ λ ) \begin{pmatrix} \lambda&&&\\ &\lambda&&\\ &&\ddots&\\ &&&\lambda\\ \end{pmatrix} λλ⋱λ
称为纯量阵。由 ( λ E ) A = λ A , A ( λ E ) = λ A (\lambda E)A=\lambda A,A(\lambda E)=\lambda A (λE)A=λA,A(λE)=λA,可知纯量阵 λ E 与矩阵 A \lambda E与矩阵A λE与矩阵A的乘积等于数 λ \lambda λ与A的乘积,当A位n阶方阵时,有
( λ E ) A n = λ A n = A n ( λ E ) (\lambda E)A_n=\lambda A_n=A_n(\lambda E) (λE)An=λAn=An(λE)
表名纯量阵 λ E \lambda E λE与任何同阶方阵都是可交换的。
矩阵的幂:设A是n阶方阵,定义 A 1 = A , A 2 = A 1 A 1 , ⋯ , A k + 1 = A k A 1 A^1=A,A^2=A^1A^1,\cdots,A^{k+1}=A^kA^1 A1=A,A2=A1A1,⋯,Ak+1=AkA1
其中 k k k为正整数。
矩阵的幂满足以下运算规律
- A K A l = A k + l , ( A k ) l = A k l A^KA^l=A^{k+l},(A^k)^l=A^{kl} AKAl=Ak+l,(Ak)l=Akl
当矩阵A与B可交换时,满足下列运算规律
- ( A B ) k = A k B k (AB)^k=A^kB^k (AB)k=AkBk
- ( A + B ) 2 = A 2 + 2 A B + B 2 (A+B)^2=A^2+2AB+B^2 (A+B)2=A2+2AB+B2
- ( A + B ) ( A − B ) = A 2 − B 2 (A+B)(A-B)=A^2-B^2 (A+B)(A−B)=A2−B2
例7 上阶例1中n元线性方程组(1)
{ a 11 x 1 + a 12 x 2 + ⋯ + a 1 n x n = b 1 , a 21 x 1 + a 22 x 2 + ⋯ + a 2 n x n = b 1 , ⋯ ⋯ ⋯ a m x 1 + a m 2 x 2 + ⋯ + a m n x n = b 1 , \begin{cases} a_{11}x_1+a_{12}x_2+\cdots+a_{1n}x_n=b_1,\\ a_{21}x_1+a_{22}x_2+\cdots+a_{2n}x_n=b_1,\\ \cdots\cdots\cdots\\ a_{m}x_1+a_{m2}x_2+\cdots+a_{mn}x_n=b_1,\\ \end{cases} ⎩ ⎨ ⎧a11x1+a12x2+⋯+a1nxn=b1,a21x1+a22x2+⋯+a2nxn=b1,⋯⋯⋯amx1+am2x2+⋯+amnxn=b1,
利用矩阵乘法可写成矩阵形式
A m × n x n × 1 = b m × 1 A_{m\times n}x_{n\times 1}=b_{m\times 1} Am×nxn×1=bm×1
其中 A = ( a i j ) A=(a_{ij}) A=(aij)为系数矩阵, x = ( x 1 x 2 ⋮ x n ) x=\begin{pmatrix}x_1\\x_2\\\vdots\\x_n\end{pmatrix} x= x1x2⋮xn 为未知数矩阵, b = ( b 1 b 2 ⋮ b m ) b=\begin{pmatrix}b_1\\b_2\\\vdots\\b_m\end{pmatrix} b= b1b2⋮bm 为常数项矩阵。特别当b=O时,得到吗哥方程的n元齐次线性方程组的矩阵形式
A m × n x n × 1 = 0 m × 1 A_{m\times n}x_{n\times 1}=0_{m\times 1} Am×nxn×1=0m×1
四、矩阵的转置
定义5 把矩阵A的行换成同序列的列得到一个新的矩阵,叫做A的转置矩阵,记作 A T A^T AT.
矩阵的转置也是一种运算,满足下列运算过滤(假设运算都是可行的):
- ( A T ) T = A (A^T)^T=A (AT)T=A
- ( A + B ) T = A T + B T (A+B)^T=A^T+B^T (A+B)T=AT+BT
- ( λ A ) T = λ A T (\lambda A)^T=\lambda A^T (λA)T=λAT
- ( A B ) T = B T A T (AB)^T=B^TA^T (AB)T=BTAT
例8 已知
A = ( 2 0 − 1 1 3 2 ) , B = ( 1 7 − 1 4 2 3 2 0 1 ) A=\begin{pmatrix} 2&0&-1\\ 1&3&2\\ \end{pmatrix} ,B=\begin{pmatrix} 1&7&-1\\ 4&2&3\\ 2&0&1\\ \end{pmatrix}\\ A=(2103−12),B= 142720−131
求 ( A B ) T (AB)^T (AB)T
A B = A = ( 0 14 − 3 17 13 10 ) ( A B ) T = ( 0 17 14 13 − 3 10 ) AB=A=\begin{pmatrix} 0&14&-3\\ 17&13&10\\ \end{pmatrix}\\ (AB)^T=\begin{pmatrix} 0&17\\ 14&13\\ -3&10\\ \end{pmatrix} AB=A=(0171413−310)(AB)T= 014−3171310
五、方阵的行列式
定义6 有n阶方阵A的元素所构成的行列式(各元素的位置不变),称为方程A的行列式,记作 d e t A 或者 ∣ A ∣ det A或者\vert A\vert detA或者∣A∣
有A确定 ∣ A ∣ \vert A\vert ∣A∣的这个运算满足下述运算规律(设A、B位n阶方阵,$\lambda $为数:
- ∣ A T ∣ = ∣ A ∣ \vert A^T\vert = \vert A\vert ∣AT∣=∣A∣
- ∣ λ A ∣ = λ n ∣ A ∣ |\lambda A\vert = \lambda^n \vert A\vert ∣λA∣=λn∣A∣
- ∣ A B ∣ = ∣ A ∣ ∣ B ∣ \vert AB\vert = \vert A\vert \vert B\vert ∣AB∣=∣A∣∣B∣
伴随矩阵:
行列式 ∣ A ∣ \vert A\vert ∣A∣的各个元素的代数余子式 A i j A_{ij} Aij所构成的如下的矩阵
A ∗ = ( A 11 A 21 ⋯ A n 1 A 12 A 22 ⋯ A n 2 ⋮ ⋮ ⋮ A 1 n A 2 n ⋯ A n n ) A^*=\begin{pmatrix} A_{11}&A_{21}&\cdots&A_{n1}\\ A_{12}&A_{22}&\cdots&A_{n2}\\ \vdots&\vdots&&\vdots\\ A_{1n}&A_{2n}&\cdots&A_{nn}\\ \end{pmatrix} A∗= A11A12⋮A1nA21A22⋮A2n⋯⋯⋯An1An2⋮Ann
称为矩阵A的伴随矩阵,简称伴随阵。
A A ∗ = A ∗ A = ∣ A ∣ E AA^*=A^*A=\vert A\vert E AA∗=A∗A=∣A∣E
结语
❓QQ:806797785
⭐️文档笔记地址 https://github.com/gaogzhen/math
参考:
[1]同济大学数学系.工程数学.线性代数 第6版 [M].北京:高等教育出版社,2014.6.p29-39.
[2]同济六版《线性代数》全程教学视频[CP/OL].2020-02-07.p9.
相关文章:

0202矩阵的运算-矩阵及其运算-线性代数
文章目录 一、矩阵的加法二、数与矩阵相乘三、矩阵与矩阵相乘四、矩阵的转置五、方阵的行列式结语 一、矩阵的加法 定义2 设有两个 m n m\times n mn橘子 A ( a i j ) 和 B ( b i j ) A(a_{ij})和B(b_{ij}) A(aij)和B(bij),那么矩阵A与B的和记为AB,规定为 A B ( a 11…...

python中的__dict__
类的__dict__返回的是:类的静态函数、类函数、普通函数、全局变量以及一些内置的属性都是放在类的__dict__里的, 而实例化对象的:__dict__中存储了一些类中__init__的一些属性值。 import的py文件 __dict__返回的是:__init__的…...

数学分析复习:无穷乘积
文章目录 无穷乘积定义:无穷乘积的收敛性命题:无穷乘积的Cauchy收敛准则正项级数和无穷乘积的联系 本篇文章适合个人复习翻阅,不建议新手入门使用 无穷乘积 设复数列 { a n } n ≥ 1 \{a_n\}_{n\geq 1} {an}n≥1,设对任意 …...

02 React 组件使用
import React, { useState } from react;// 定义一个简单的函数式组件 function Counter() {// 使用 useState hook 来创建一个状态变量 count,并提供修改该状态的函数 setCountconst [count, setCount] useState(0);// 在点击按钮时增加计数器的值const increment…...
你就是上帝
你就是上帝:Jv程序员,请你站在上帝或神的角度 1.万物皆有裂缝 按照西方文化(宗教神话,古希腊、古罗马等),上帝创建了人; 创建人之前,还创建了人的居所或地盘/栖息地(伊…...

Spring Cloud: openFegin使用
文章目录 一、OpenFeign简介二、Springboot集成OpenFeign1、引入依赖2、EnableFeignClients注解(1)应用(2)属性解析 3、 FeignClient(1)应用(2)属性解析(3)向…...

流畅的 Python 第二版(GPT 重译)(二)
第三章:字典和集合 Python 基本上是用大量语法糖包装的字典。 Lalo Martins,早期数字游牧民和 Pythonista 我们在所有的 Python 程序中都使用字典。即使不是直接在我们的代码中,也是间接的,因为dict类型是 Python 实现的基本部分。…...

Flutter 旋转动画 线性变化的旋转动画
直接上代码 图片自己添加一张就好了 import dart:math;import package:flutter/material.dart;import package:flutter/animation.dart;void main() > runApp(MyApp()); //旋转动画 class MyApp extends StatelessWidget {overrideWidget build(BuildContext context) {re…...

【Web应用技术基础】HTML(5)——案例1:展示简历信息
样式: 代码: <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>展示简历信息…...
)
ethers.js:wallet(创建钱包,导入助记词,导入私钥)
Wallet Wallet类继承了Signer,可以使用私钥作为外部拥有帐户(EOA)的标准对交易和消息进行签名。 npm install ethers@5.4.0// 引入 import {ethers } from ethers创建新钱包 this.provider = new ethers.providers.Web3Provider(window...

面试笔记——Java集合篇
Java集合框架体系 重点:单列集合——ArrayList、LinkedList;双列集合——HashMap、ConcurrentHashMap。 List相关 数组(Array) 是一种用连续的内存空间存储相同数据类型数据的线性数据结构。 数组获取其他元素: 为什…...

在 IntelliJ IDEA 中使用 Terminal 执行 git log 命令后的退出方法
前言 IntelliJ IDEA 是一款广受欢迎的集成开发环境,它内置了强大的终端工具,使得开发者无需离开IDE就能便捷地执行各种命令行操作,包括使用 Git 进行版本控制。在 IDEA 的 Terminal 中执行 git log 命令时,由于该命令会显示项目的…...
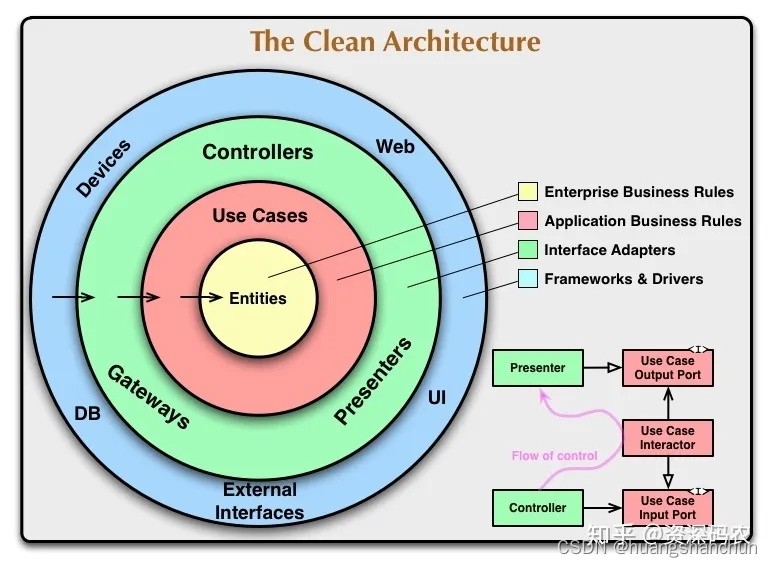
架构整洁之道-读书总结
1 概述 1.1 关于本书 《架构整洁之道》(Clean Architecture: A Craftsman’s Guide to Software Structure and Design)是由著名的软件工程师Robert C. Martin(又称为Uncle Bob)所著。这本书提供了软件开发和架构设计的指导原则…...

蓝桥杯学习笔记(贪心)
在很久很久以前,有几个部落居住在平原上,依次编号为1到n。第之个部落的人数为 t 有一年发生了灾荒,年轻的政治家小蓝想要说服所有部落一同应对灾荒,他能通过谈判来说服部落进行联台。 每次谈判,小蓝只能邀请两个部落参…...

【无标题】如何使用 MuLogin 设置代理
如何使用 MuLogin 设置代理 使用 MuLogin 浏览器设置我们的代理,轻松管理多个社交媒体或电子商务帐户。 什么是MuLogin? MuLogin 是一款虚拟反检测浏览器,使用户能够管理多个电子商务、社交媒体和广告帐户,而无需验证码或 IP 禁…...

芒果YOLOv8改进135:主干篇GCNet,统一为全局上下文建模global context结构,即插即用,助力小目标检测,轻量化的同时精度性能涨点
该专栏完整目录链接: 芒果YOLOv8深度改进教程 芒果专栏 基于 GCNet 的改进结构,改进源码教程 | 详情如下🥇 💡本博客 改进源代码改进 适用于 YOLOv8 按步骤操作运行改进后的代码即可 即插即用 结构。博客 包括改进所需的 核心结构代码 文件 论文:https://arxiv.org/a…...
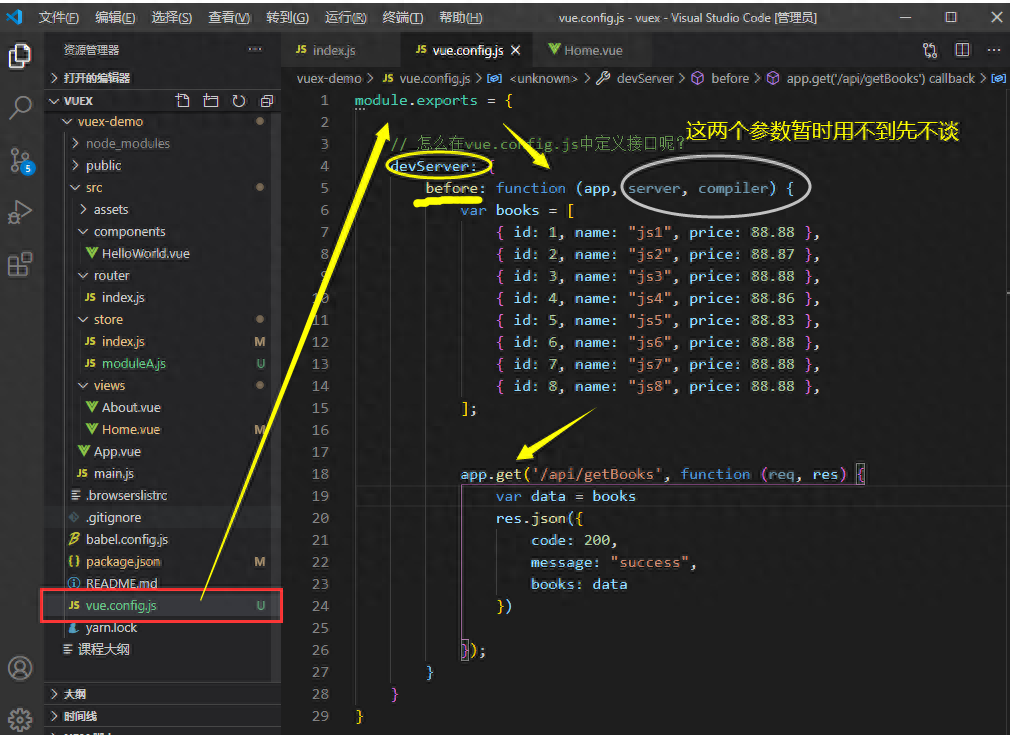
全面:vue.config.js 的完整配置
vue.config.js是Vue项目的配置文件,用于配置项目的构建、打包和开发环境等。 在Vue CLI 3.0之后,项目的配置文件从原来的build和config目录下的多个配置文件,合并成了一个vue.config.js文件。这个文件可以放在项目的根目录下,用于…...

海量数据处理项目-账号微服务注册Nacos+配置文件增加
海量数据处理项目-账号微服务注册Nacos配置文件增加 导入生成好的代码 model (为啥不放common项目,如果是确定每个服务都用到的依赖或者类才放到common项目) mapper 类接口拷贝 resource/mapper文件夹 xml脚本拷贝 controller service 不拷贝 Mybatis plus配置控制…...

DNS 服务 Unbound 部署最佳实践
文章目录 安装unbound-control配置启动服务测试 参考: 官网地址:https://nlnetlabs.nl/projects/unbound/about/ 详细文档:https://unbound.docs.nlnetlabs.nl/en/latest/index.html DNS服务Unbound部署于使用 https://cloud.tencent.com/…...
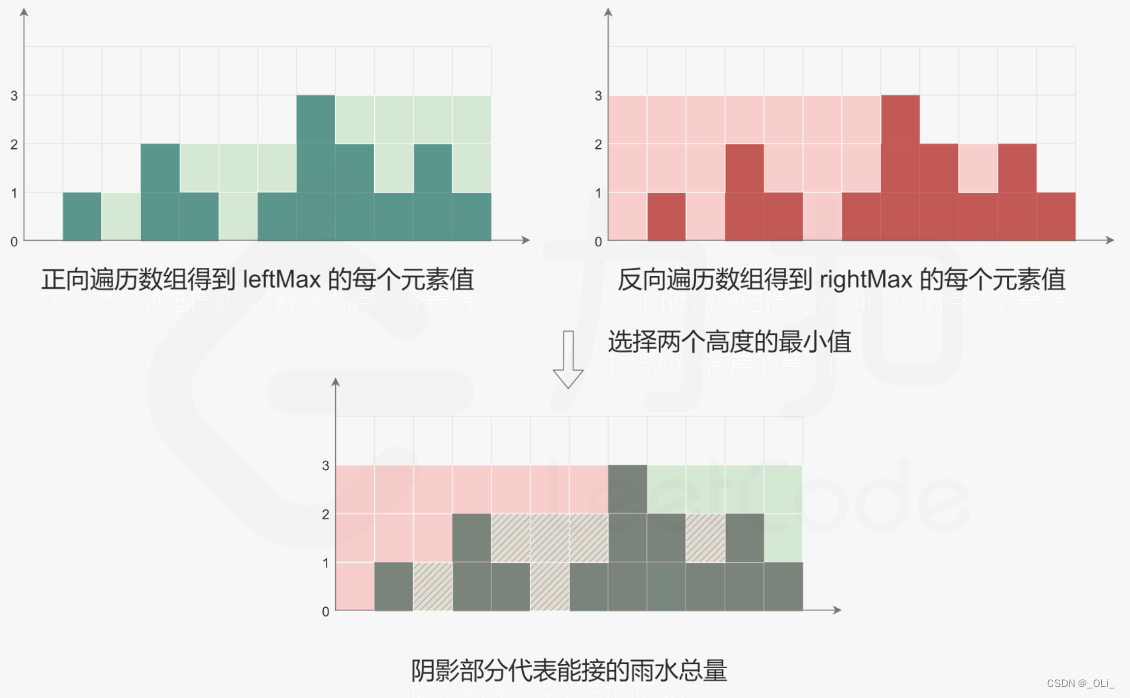
力扣HOT100 - 42. 接雨水
解题思路: 动态规划 感觉不是很好想 class Solution {public int trap(int[] height) {int n height.length;if (n 0) return 0;int[] leftMax new int[n];leftMax[0] height[0];for (int i 1; i < n; i) {leftMax[i] Math.max(leftMax[i - 1], height[i…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...

使用SSE解决获取状态不一致问题
使用SSE解决获取状态不一致问题 1. 问题描述2. SSE介绍2.1 SSE 的工作原理2.2 SSE 的事件格式规范2.3 SSE与其他技术对比2.4 SSE 的优缺点 3. 实战代码 1. 问题描述 目前做的一个功能是上传多个文件,这个上传文件是整体功能的一部分,文件在上传的过程中…...

用 Rust 重写 Linux 内核模块实战:迈向安全内核的新篇章
用 Rust 重写 Linux 内核模块实战:迈向安全内核的新篇章 摘要: 操作系统内核的安全性、稳定性至关重要。传统 Linux 内核模块开发长期依赖于 C 语言,受限于 C 语言本身的内存安全和并发安全问题,开发复杂模块极易引入难以…...

spring boot使用HttpServletResponse实现sse后端流式输出消息
1.以前只是看过SSE的相关文章,没有具体实践,这次接入AI大模型使用到了流式输出,涉及到给前端流式返回,所以记录一下。 2.resp要设置为text/event-stream resp.setContentType("text/event-stream"); resp.setCharacter…...
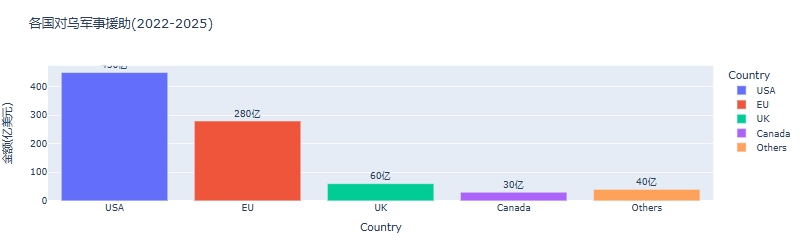
python可视化:俄乌战争时间线关键节点与深层原因
俄乌战争时间线可视化分析:关键节点与深层原因 俄乌战争是21世纪欧洲最具影响力的地缘政治冲突之一,自2022年2月爆发以来已持续超过3年。 本文将通过Python可视化工具,系统分析这场战争的时间线、关键节点及其背后的深层原因,全面…...
