[Python图像处理] 使用高通滤波器实现同态滤波
使用高通滤波器实现同态滤波
- 同态滤波基础
- 实现同态滤波
- 相关链接
同态滤波基础
同态滤波是一种去除图像中乘性噪声的技术,常用于校正图像中的不均匀照明。根据图像形成的光照反射模型,图像 f(x,y)f(x,y)f(x,y) 可以由以下两个分量表征:
- 入射到场景中的光源量
- 场景中对象反射的光量
根据光照反射模型模型,图像中像素的强度(即对象上的点反射的光)是场景照明和场景中对象反射的结果。傅立叶变换在加法下是线性关联的,但在乘法下并不关联。因此,傅立叶方法仅在将噪声作为原始图像的附加项建模时,才适合从图像中去除噪声。
但是,如果图像的缺陷(例如,不均匀的照明)必须建模为乘法而非加法,则直接应用傅立叶变换并不合适。此时,我们便需要使用同态滤波:首先,通过使用对数将乘法转换为加法;然后,使用对数域中的 HPF 来删除低频照明分量,同时保留高频反射率分量。
同态滤波的基本步骤如下,输入图像为 f(x,y)f(x,y)f(x,y),滤波器的输出为 g(x,y)g(x,y)g(x,y):

实现同态滤波
在本节中,我们将学习如何使用 Butterworth HPF 实现同态滤波器。
(1) 首先,导入所需 Python 库,并定义相关函数:
import cv2
import numpy as np
import matplotlib.pyplot as plt
from skimage.color import rgb2gray
from skimage.filters import sobel, threshold_otsudef dft2(im):freq = cv2.dft(np.float32(im), flags = cv2.DFT_COMPLEX_OUTPUT)freq_shift = np.fft.fftshift(freq)mag, phase = freq_shift[:,:,0], freq_shift[:,:,1]return mag + 1j*phasedef idft2(freq):real, imag = freq.real, freq.imagback = cv2.merge([real, imag])back_ishift = np.fft.ifftshift(back)im = cv2.idft(back_ishift, flags=cv2.DFT_SCALE)im = cv2.magnitude(im[:,:,0], im[:,:,1])return imdef butterworth(sz, D0, n=1):h, w = szu, v = np.meshgrid(range(-w//2,w//2), range(-h//2,h//2)) #, sparse=True)return 1 / (1 + (D0/(0.01+np.sqrt(u**2 + v**2)))**(2*n))
(2) 定义同态滤波函数,频域 H(u,v)H(u,v)H(u,v) 中的同态滤波器如下所示:
H(u,v)=(γH−γL)(11+(D0D(u,v))2n)+γLH(u,v)=(\gamma_H-\gamma_L)(\frac 1 {1+(\frac {D_0} {D(u,v)})^{2n}})+\gamma_L H(u,v)=(γH−γL)(1+(D(u,v)D0)2n1)+γL
为了避免对数域中错误操作,在输入中添加常数 1,以确保对数的输入始终 ≥1,最后,从输出中减去 1:
def homomorphic_filter(im, D0, g_l=0, g_h=1, n=1):im_log = np.log(im.astype(np.float)+1)im_fft = dft2(im_log)H = (g_h - g_l) * butterworth(im.shape, D0, n) + g_l#H = np.fft.ifftshift(H)im_fft_filt = H*im_fft#im_fft_filt = np.fft.ifftshift(im_fft_filt)im_filt = idft2(im_fft_filt)im = np.exp(im_filt.real)-1im = np.uint8(255*im/im.max())return im
(3) 读取输入图像(带有不均匀照明),将其转换为灰度图像(确保像素值在 0-255 范围内),然后通过调函数 homomorphic_filter() 应用同态滤波器。
其中,Butterworth 滤波器 n=2 阶的截止频率为 30,γL\gamma_LγL 和 γH\gamma_HγH 参数分别设置为 0.3 和 1:
image = rgb2gray(plt.imread('1.png'))
image_filtered = homomorphic_filter(image, D0=30, n=2, g_l=0.3, g_h=1)
(4) 使用 sobel 滤波器从原始图像中提取边缘,使用 OTSU 最佳阈值创建二值图像如下:
image_edges = sobel(image)
image_edges = image_edges <= threshold_otsu(image_edges)
(5) 使用 sobel 滤波器通过从同态滤波器转换的图像中提取边缘:
image_filtered_edges = sobel(image_filtered)
image_filtered_edges = image_filtered_edges <= threshold_otsu(image_filtered_edges)
(6) 最后,绘制输入图像和使用同态滤波器获得的输出图像,以及提取的边缘:
plt.figure(figsize=(21,17))
plt.gray()
plt.subplots_adjust(0,0,1,0.95,0.01,0.05)
plt.subplot(221), plt.imshow(image), plt.axis('off'), plt.title('original image', size=10)
plt.subplot(222), plt.imshow(image_filtered), plt.axis('off'), plt.title('filtered image', size=10)
plt.subplot(223), plt.imshow(image_edges), plt.axis('off'), plt.title('original image edges', size=10)
plt.subplot(224), plt.imshow(image_filtered_edges), plt.axis('off'), plt.title('filtered image edges', size=10)
plt.show()
输出结果如下所示:

从上图中可以看出,所获得的输出图像中的光照更加均匀,从而可以看清楚原始图像中黑暗区域的细节/边缘。
相关链接
Python图像处理【1】图像与视频处理基础
Python图像处理【2】探索Python图像处理库
Python图像处理【3】Python图像处理库应用
Python图像处理【4】图像线性变换
Python图像处理【5】图像扭曲/逆扭曲
Python图像处理【7】采样、卷积与离散傅里叶变换
相关文章:

[Python图像处理] 使用高通滤波器实现同态滤波
使用高通滤波器实现同态滤波同态滤波基础实现同态滤波相关链接同态滤波基础 同态滤波是一种去除图像中乘性噪声的技术,常用于校正图像中的不均匀照明。根据图像形成的光照反射模型,图像 f(x,y)f(x,y)f(x,y) 可以由以下两个分量表征: 入射到…...
PyTorch深度学习:60分钟入门
PyTorch深度学习:60分钟入门 本教程的目的: 更高层级地理解PyTorch的Tensor库以及神经网络。训练一个小的神经网络来对图像进行分类。 本教程以您拥有一定的numpy基础的前提下展开 Note: 务必确认您已经安装了 torch 和 torchvision 两个包。 这是一个基于Pytho…...

C语言指针常见问题汇总
我们在学C语言时,指针是我们最头疼的问题之一,针对C语言指针,博主根据自己的实际学到的知识以及开发经验,总结了以下使用C语言指针时常见问题。 1、指针做函数参数 学习函数的时候,讲了函数的参数都是值拷贝…...
Coremail邮件系统全新上线存档邮箱功能
邮箱积累邮件太多,搜索起来又慢又麻烦! 我的重要邮件忘记下载丢失了!14天自动删除太难了! 有没有可能重要邮件自动存档,解救一下“遗忘星”人? 在我们日常工作中,邮件是最经常使用的办公工具之一…...
Python绘图
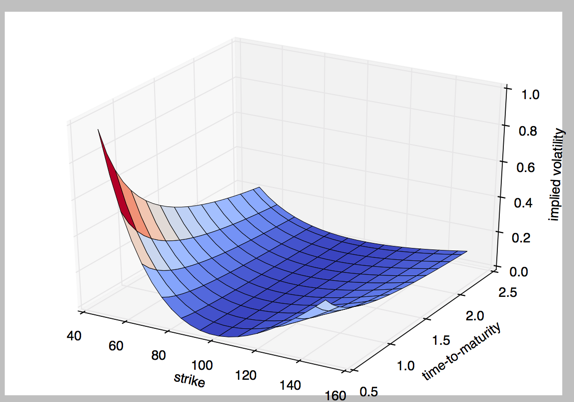
1.二维绘图 a. 一维数据集 用 Numpy ndarray 作为数据传入 ply 1. import numpy as np import matplotlib as mpl import matplotlib.pyplot as pltnp.random.seed(1000) y np.random.standard_normal(10) print "y %s"% y x range(len(y)) print "x%s&q…...
)
【独家】华为OD机试 - 第K个最小码值的字母(C 语言解题)
最近更新的博客 华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典【华为OD机试】全流程解析经验分享,题型分享,防作弊指南)华为od机试,独家整理 已参加机试…...
)
整数反转(python)
题目链接: https://leetcode.cn/problems/reverse-integer/ 题目描述: 给你一个 32 位的有符号整数 x ,返回将 x 中的数字部分反转后的结果。 如果反转后整数超过 32 位的有符号整数的范围 [−231,231−1][−2^{31}, 2^{31} − 1][−231,231…...
【数据结构】二叉树与堆
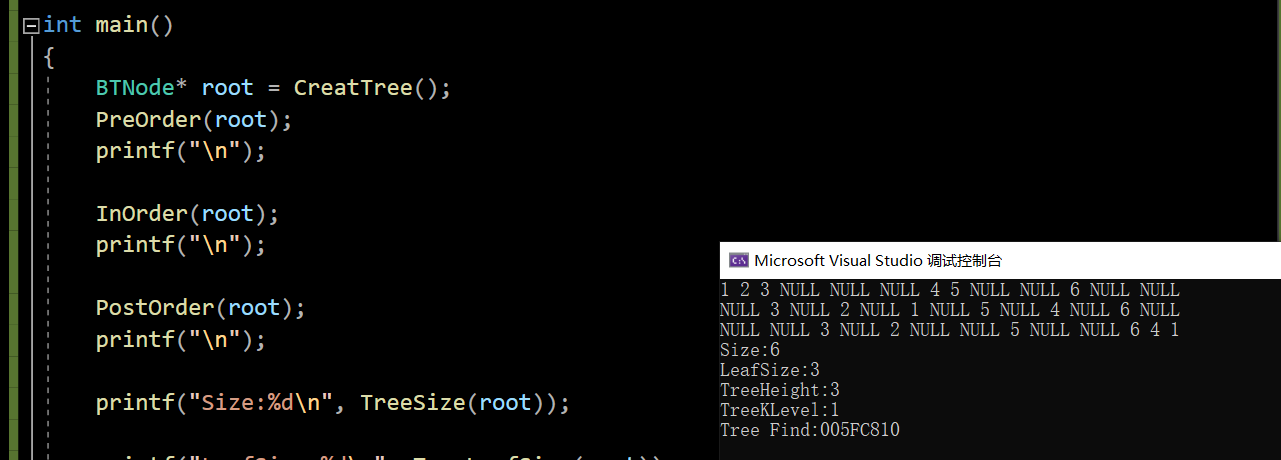
文章目录1.树概念及结构1.1树的相关概念1.2树的结构2.二叉树概念及结构2.1相关概念2.2特殊的二叉树2.3二叉树的性质2.4二叉树的存储结构3.二叉树的顺序结构及实现3.1二叉树的顺序结构3.2堆的概念3.3堆的实现Heap.hHeap.c3.4堆的应用3.4.1 堆排序3.4.2 TOP-KOJ题最小K个数4.二叉…...
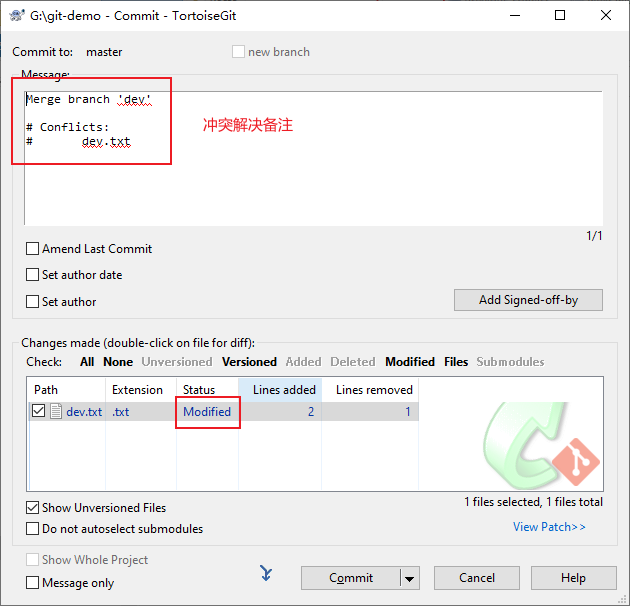
Git图解-常用命令操作-可视化
目录 一、前言 二、初始化仓库 2.1 设置用户名与邮箱 2.2 初始化仓库 三、添加文件 四、查看文件状态 五、查看提交日志 六、查看差异 七、版本回退 八、删除文件 九、分支管理 9.1 创建分支 9.2 切换分支 9.3 查看分支 9.4 合并分支 十、文件冲突 十一、转视…...

C语言-基础了解-20-typedef
typedef 一、typedef C 语言提供了 typedef 关键字,您可以使用它来为类型取一个新的名字。下面的实例为单字节数字定义了一个术语 BYTE: typedef unsigned char BYTE; 在这个类型定义之后,标识符 BYTE 可作为类型 unsigned char 的缩写&…...

Ubuntu系统升级16.04升级18.04
一、需求说明 作为Linux发行版中的后起之秀,Ubuntu 在短短几年时间里便迅速成长为从Linux初学者到实验室用计算机/服务器都适合使用的发行版,目前官网最新版本是22.04。Ubuntu16.04是2016年4月发行的版本,于2019年4月停止更新维护。很多软件支…...
CM6.3.2启用Kerberos(附问题解决)
基础准备支持JCE的jdk重新安装JCE的jdk(已正确配置跳过)删除/usr/java/下面的jdk,然后通过CM->管理->安全->安装Java无限制...重新安装后,配置Java(可选)主机->主机配置->搜java->Java主目录 配置路径主机->所有主机->设置->高级:Java配置Kerberos安…...
)
QML 动画(组合动画)
在QML中,可以把多个动画组合成一个单一的动画。 组合动画的类型: ParallelAnimation 动画同时进行(并行)SequentialAnimation 动画按照顺序执行(顺序执行)注意:将动画分组为“顺序动画”或“…...
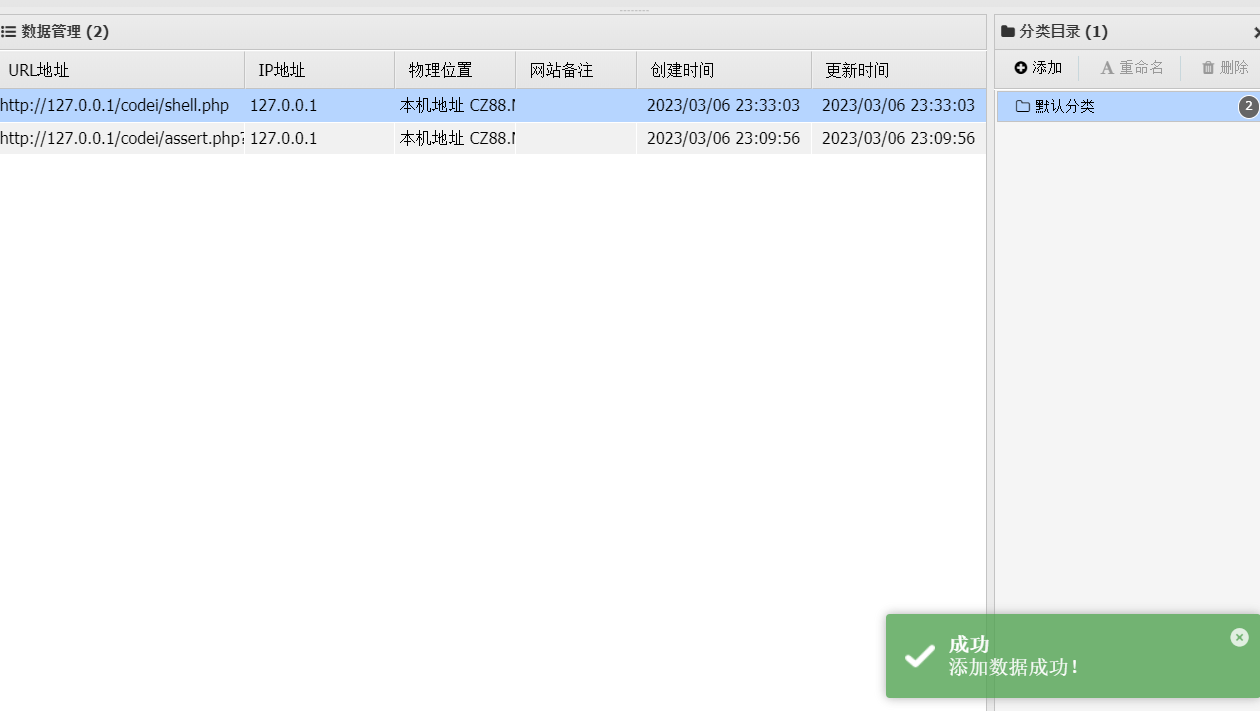
【PHP代码注入】PHP代码注入漏洞
漏洞原理RCE为两种漏洞的缩写,分别为Remote Command/Code Execute,远程命令/代码执行PHP代码注入也叫PHP代码执行(Code Execute)(Web方面),是指应用程序过滤不严,用户可以通过HTTP请求将代码注入到应用中执行。代码注入(代码执行)…...

Python 常用语句同C/C++、Java的不同
文章目录前言1. 数字 int2. 字符 string3. 列表 List4. 元组 tuple5. 字典 dictionary6. 集合 set7. 值类型变量与引用类型变量8. if elif else9. >、<、>、<、、!10. while11. for前言 本篇为本人前段时间的一个简单汇总,这里可能并不齐全,…...

一把火烧掉了苹果摆脱中国制造的幻想,印度制造难担重任
这几年苹果不断推动印度制造,希望摆脱对中国制造的依赖,然而近期苹果在印度的一家代工厂发生大火却证明了苹果的这一计划遭受重大打击,印度制造根本就无法中国制造。一、印度制造屡屡发生幺蛾子苹果推动印度制造已有多年了,然而印…...

常用的 JavaScript 数组 API
以下是一些常用的 JavaScript 数组 API 的代码示例: 1、push() push(): 在数组末尾添加一个或多个元素,返回新的数组长度 const arr [1, 2, 3]; const newLength arr.push(4, 5); console.log(arr); // [1, 2, 3, 4, 5] console.log(newLength); //…...
海思3531a pjsip交叉编译
学习文档: PJSUA2 Documentation — PJSUA2 Documentation 1.0-alpha documentationhttps://www.pjsip.org/docs/book-latest/html/index.html ./configure --prefix/opensource/pjproject-2.12/build3531a \ --host/opt/hisi-linux/x86-arm/arm-hisi…...
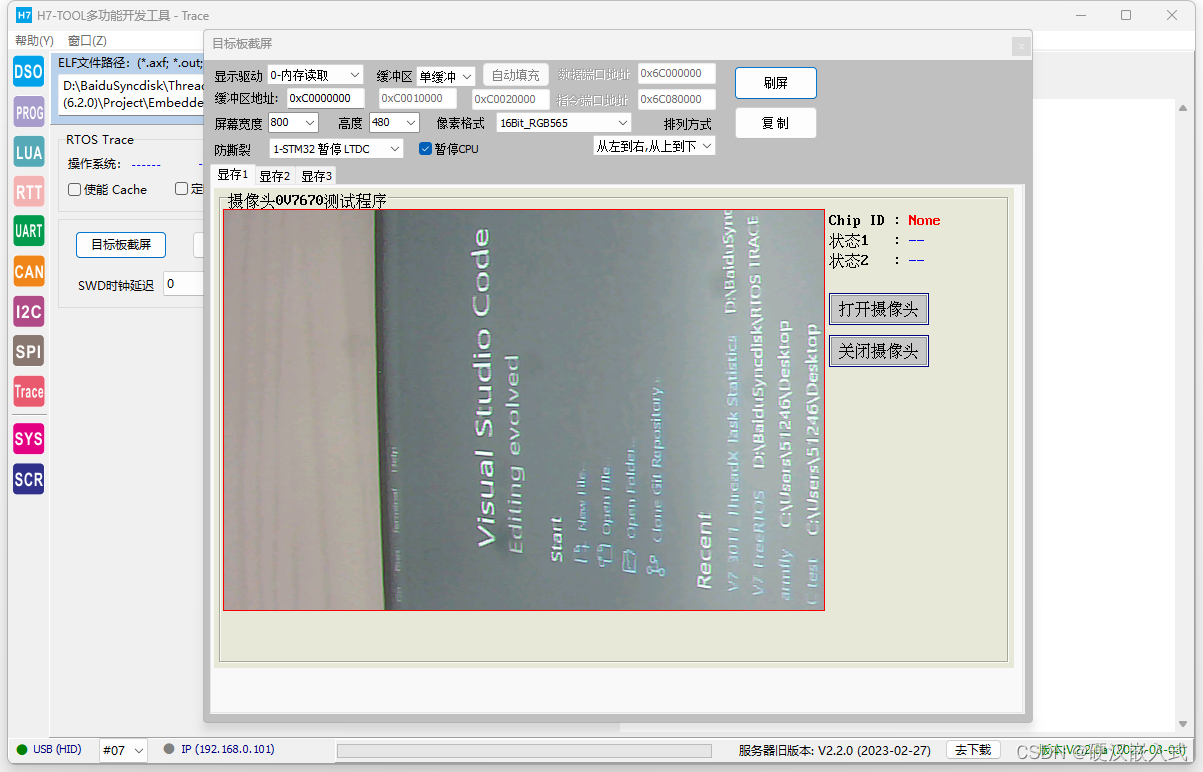
《安富莱嵌入式周报》第305期:超级震撼数码管瀑布,使用OpenAI生成单片机游戏代码的可玩性,120通道逻辑分析仪,复古电子设计,各种运动轨迹函数源码实现
往期周报汇总地址:嵌入式周报 - uCOS & uCGUI & emWin & embOS & TouchGFX & ThreadX - 硬汉嵌入式论坛 - Powered by Discuz! 说明: 谢谢大家的关注,继续为大家盘点上周精彩内容。 视频版: https://www.bi…...

力扣-查找每个员工花费的总时间
大家好,我是空空star,本篇带大家了解一道简单的力扣sql练习题。 文章目录前言一、题目:1741. 查找每个员工花费的总时间二、解题1.正确示范①提交SQL运行结果2.正确示范②提交SQL运行结果3.正确示范③提交SQL运行结果4.正确示范④提交SQL运行…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...
