【面试经典150 | 动态规划】三角形最小路径和
文章目录
- 写在前面
- Tag
- 题目来源
- 解题思路
- 方法一:动态规划
- 写在最后
写在前面
本专栏专注于分析与讲解【面试经典150】算法,两到三天更新一篇文章,欢迎催更……
专栏内容以分析题目为主,并附带一些对于本题涉及到的数据结构等内容进行回顾与总结,文章结构大致如下,部分内容会有增删:
- Tag:介绍本题牵涉到的知识点、数据结构;
- 题目来源:贴上题目的链接,方便大家查找题目并完成练习;
- 题目解读:复述题目(确保自己真的理解题目意思),并强调一些题目重点信息;
- 解题思路:介绍一些解题思路,每种解题思路包括思路讲解、实现代码以及复杂度分析;
- 知识回忆:针对今天介绍的题目中的重点内容、数据结构进行回顾总结。
Tag
【动态规划】【数组】
题目来源
120. 三角形最小路径和

解题思路
方法一:动态规划
定义状态
f[i][j] 表示从三角形顶部到达位置 (i, j) 的最小路径,i 和 j 分别表示 triangle 数组中的第 i 个数组中的第 j 个元素(索引从 0 开始)。
转移关系
由于每一步只能移动到下一行的「相邻节点」,因此要到达位置 (i, j) 处,上一步只能在位置 (i-1, j) 或 (i-1, j-1)。我们需要在这两个位置中选择一个路径和较小的进行转移,转移关系为:
f [ i ] [ j ] = m i n ( f [ i − 1 ] [ j ] , f [ i − 1 ] [ j − 1 ] ) + t r i a n g l e [ i ] [ j ] f[i][j] = min(f[i-1][j], f[i-1][j-1]) + triangle[i][j] f[i][j]=min(f[i−1][j],f[i−1][j−1])+triangle[i][j]
base case
边界情况有三种,一是初始位置 f[0][0] = triangle[0][0].
二是对于每个数组中的第一个位置,即 f[i][j] 中 j = 0 的情况,上一个位置只能是 (i-1, j),因此此时有:
f [ i ] [ 0 ] = f [ i − 1 ] [ j ] + t r i a n g l e [ i ] [ j ] , i > = 1 f[i][0] = f[i-1][j] + triangle[i][j], i>=1 f[i][0]=f[i−1][j]+triangle[i][j],i>=1
三是 i = j 时,上一个位置只能是 (i-1, j-1),因此有:
f [ i ] [ i ] = f [ i − 1 ] [ i − 1 ] + t r i a n g l e [ i ] [ i ] , i = j f[i][i] = f[i-1][i-1] + triangle[i][i], i=j f[i][i]=f[i−1][i−1]+triangle[i][i],i=j
最后返回
最后返回数组 f[n-1] 中的最小值。
实现代码
class Solution {
public:int minimumTotal(vector<vector<int>>& triangle) {int n = triangle.size();vector<vector<int>> f(n, vector<int>(n));f[0][0] = triangle[0][0];for (int i = 1; i < n; ++i) {f[i][0] = f[i-1][0] + triangle[i][0];for (int j = 1; j < i; ++j) {f[i][j] = min(f[i-1][j], f[i-1][j-1]) + triangle[i][j];}f[i][i] = f[i-1][i-1] + triangle[i][i];}return *min_element(f[n-1].begin(), f[n-1].end());}
};
复杂度分析
时间复杂度: O ( n 2 ) O(n^2) O(n2), n n n 是三角形的行数。
空间复杂度: O ( n 2 ) O(n^2) O(n2)。我们需要一个 n × n n \times n n×n 的二维数组存放所有的状态。
写在最后
如果您发现文章有任何错误或者对文章有任何疑问,欢迎私信博主或者在评论区指出 💬💬💬。
如果大家有更优的时间、空间复杂度的方法,欢迎评论区交流。
最后,感谢您的阅读,如果有所收获的话可以给我点一个 👍 哦。
相关文章:

【面试经典150 | 动态规划】三角形最小路径和
文章目录 写在前面Tag题目来源解题思路方法一:动态规划 写在最后 写在前面 本专栏专注于分析与讲解【面试经典150】算法,两到三天更新一篇文章,欢迎催更…… 专栏内容以分析题目为主,并附带一些对于本题涉及到的数据结构等内容进行…...

【线段树二分】第十三届蓝桥杯省赛C++ A组/研究生组 Python 研究生组《扫描游戏》(C++)
【题目描述】 有一根围绕原点 O 顺时针旋转的棒 OA,初始时指向正上方(Y 轴正向)。 在平面中有若干物件,第 i 个物件的坐标为(,),价值为 。 当棒扫到某个物件时,棒的长度会瞬间增长 ÿ…...

类模板与继承及成员、全局函数的实现
一、类模板与继承 当类模板碰到继承时,需要注意一下几点: 1.当子类继承的父类是一个类模板时,子类在声明的时候,要指定出父类中T的类型 2.如果不指定,编译器无法给子类分配内存 3.如果想灵活指定出父类中T的类型&a…...
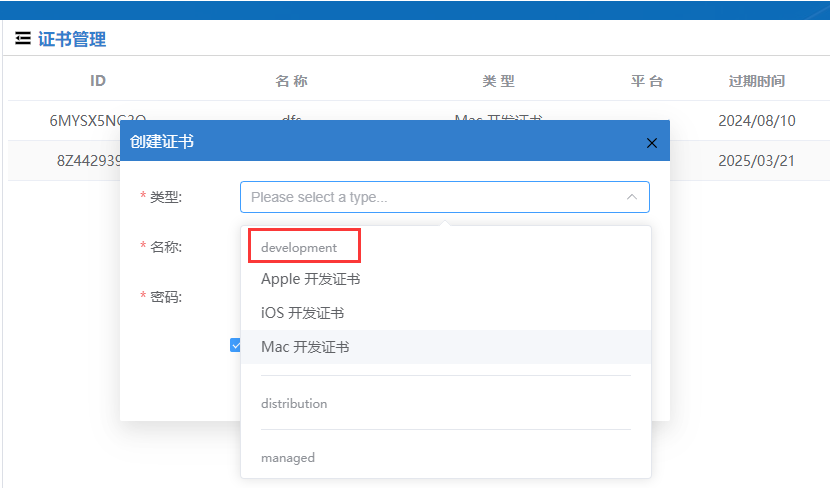
怎么制作iOS证书
首先我们登录appuploder官网 搜索 appuploder 第一个就是我们官网啦,网址是:Appuploader home -- A tool improve ios develop efficiency such as submit ipa to appstore and manage ios certificate 可以跨平台开发,无论是Windows还是Ma…...
图床项目实战:从零搭建一个简易图床
项目背景与需求分析 随着互联网的发展,图片分享、存储和管理的需求日益增长。图床作为一种专门用于存储和分享图片的服务,受到了广大用户的欢迎。本项目旨在搭建一个简易的图床系统,满足用户上传、查看和删除图片的基本需求。 技术选型 本项…...

双亲委派机制总结
回顾了一下双亲委派机制,在这记录记录,下一篇会基于打破双亲委派机制来更新 1. 类加载: 多个java文件经过编译打包后生成可运行jar包,最后启动程序。首先需要通过类加载器把主类加载到JVM。主类在运行过程中如果使用到其他类&a…...
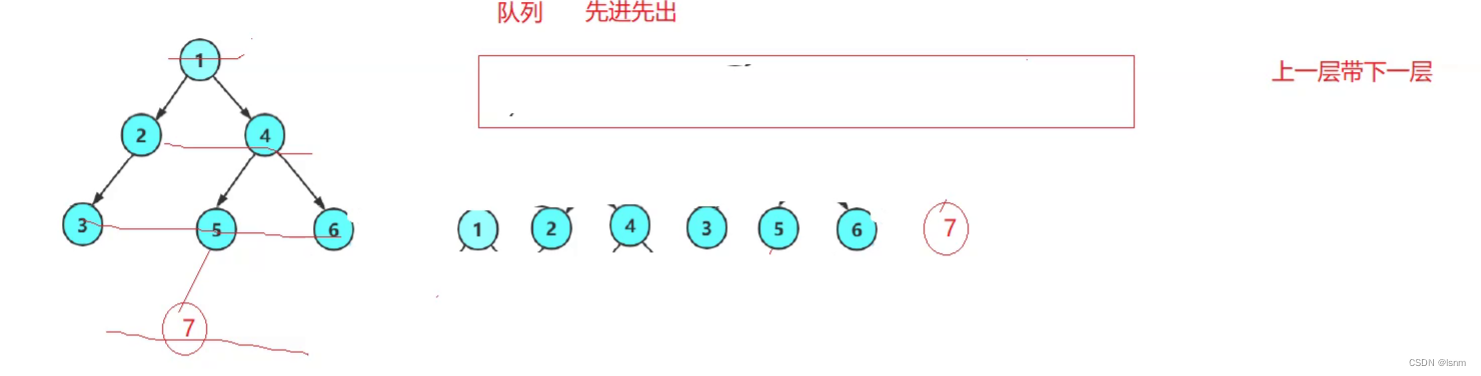
C语言数据结构基础————二叉树学习笔记(四)简单的OJ题目练习
1.单值二叉树 965. 单值二叉树 - 力扣(LeetCode) 建立一个新的函数,用函数传参的方法来记录val的值 如上一篇最后的对称二叉树的习题,建立新的函数来传参 多采用使用反对值的方法,因为如果是相等return true的话&am…...
:生成一个比较综合的message)
protobuf学习笔记(一):生成一个比较综合的message
一年前学过对应的知识,终究是太潦草了,这几天网上学习了一下,重新写一下笔记。这里是protobuf和golang的结合 一、protobuf protobuf实际上是一种类似json和gob之类的数据格式,也是grpc的御用格式吧(有自己的优势&am…...
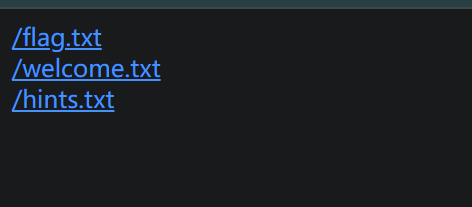
[BT]BUUCTF刷题第8天(3.26)
第8天 Web [CISCN2019 华北赛区 Day2 Web1]Hack World 题目明确提示flag在flag表里的flag列,这里先尝试1 返回:你好,glzjin想要一个女朋友。 再尝试1,返回bool(false) 到这里就感觉是布尔盲注的题目类型了(虽然我没…...

【前端】-
相对路径和绝对路径是描述文件位置的两种方式。 1. 相对路径:相对于自己的目标文件的位置,以引用文件之间网页所在位置为参考基础,而建立出的目录路径。因此,当保存于不同目录的网页引用同一个文件时,所使用的路径将不…...
uniapp安装axios
先npm安装 npm i axios然后在项目里面建一个utils文件,再建一个index.js 以下是index.js代码: import axios from axios; const service axios.create({baseURL: //xxxx.xxxxx.com///你的请求接口域名, timeout: 6000, // request timeoutcrossDomai…...
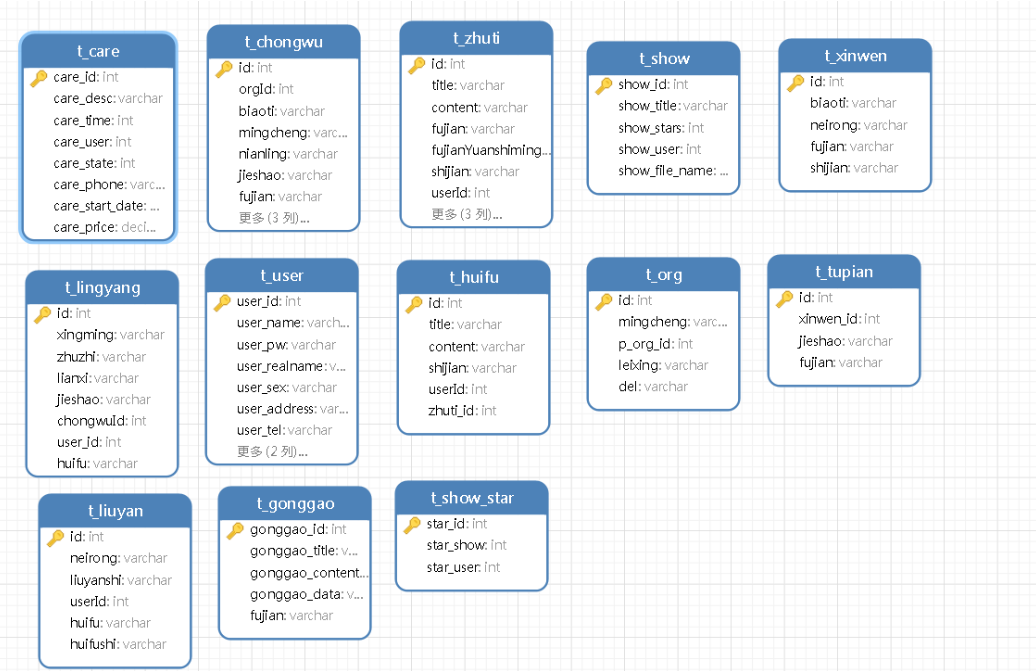
基于javaweb宠物领养平台管理系统设计和实现
基于javaweb宠物领养平台管理系统设计和实现 博主介绍:多年java开发经验,专注Java开发、定制、远程、文档编写指导等,csdn特邀作者、专注于Java技术领域 作者主页 央顺技术团队 Java毕设项目精品实战案例《1000套》 欢迎点赞 收藏 ⭐留言 文末获取源码联…...

网络问题排查方案
PC上不了网初步排查方案步骤 首先查看配置是否正确,是否使用自动获取(DHCP)IP,掩码,网关,如果不是,手动配置确认网关,子网掩码,IP是否配置正确,IP是否已有PC使…...

【CMake】所见所闻所学
Note: 本贴仅记录遇到的CMake的问题,以问题为驱动。 - cmake_minimum_required - project - add_executable - target_include_directories - ExternalProject_Add ExternalProject_Add 是 CMake 中用于管理和构建外部项目的模块。通过 ExternalProject_Add&…...

Linux shell脚本切换为root用户执行命令
首先安装expect。 sudo apt install expect 创建shell脚本文件,示例内容如下: #!/usr/bin/expectspawn su rootexpect {"密码:" {send "00000\r"}"Password:" {send "000000\r"}}send "./…...

儿童护眼灯哪个牌子好?盘点五款满分护眼台灯
为人父母以后,守护孩子的健康成了首要任务。随着孩子慢慢长大,课程的增多,作业也随之增加起来。很多孩子从放学回家就开始伏案在桌子上写作业,哪怕天色逐渐变暗,孩子作业仍旧未写完,作为父母的我们不得不担…...

HangZhou Java Journey P1
Java程序运行时类加载机制 下面是对这个流程的详细说明: JVM启动:当Java程序开始执行时,JVM首先启动。JVM的启动涉及到操作系统级别的进程创建和资源分配。 Bootstrap ClassLoader:JVM启动后,首先会初始化Bootstrap …...
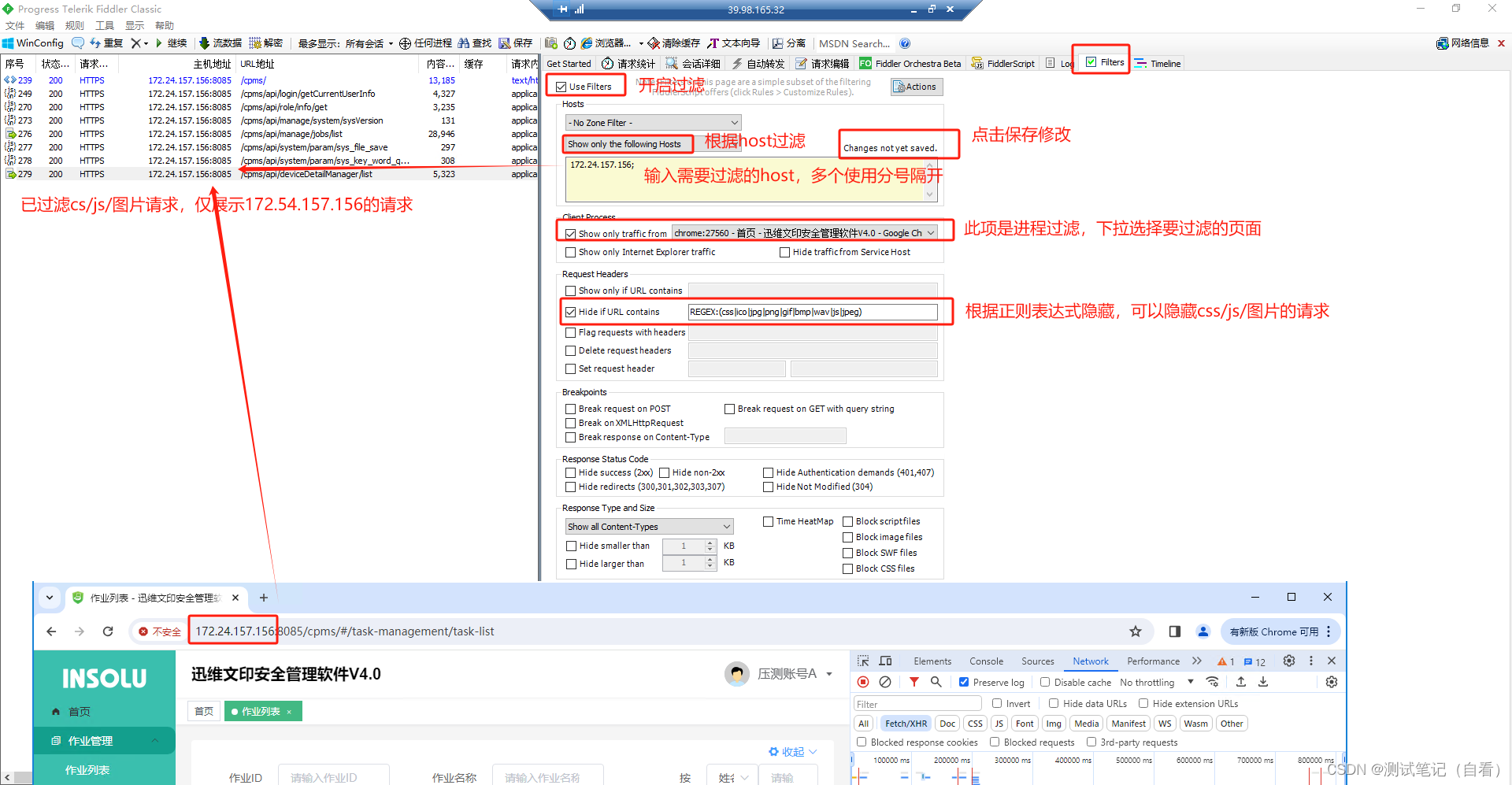
fiddler过滤器使用,隐藏图片、js、css请求
如果抓包过程中不想查看图片、js、css请求,或者只想抓某个ip或者某个网页下的请求,可以在过滤器中设置。 (1)没有开启过滤器 可以看出所有的请求都会抓取,cs、js、图片请求都有 (2)开启过滤器 …...
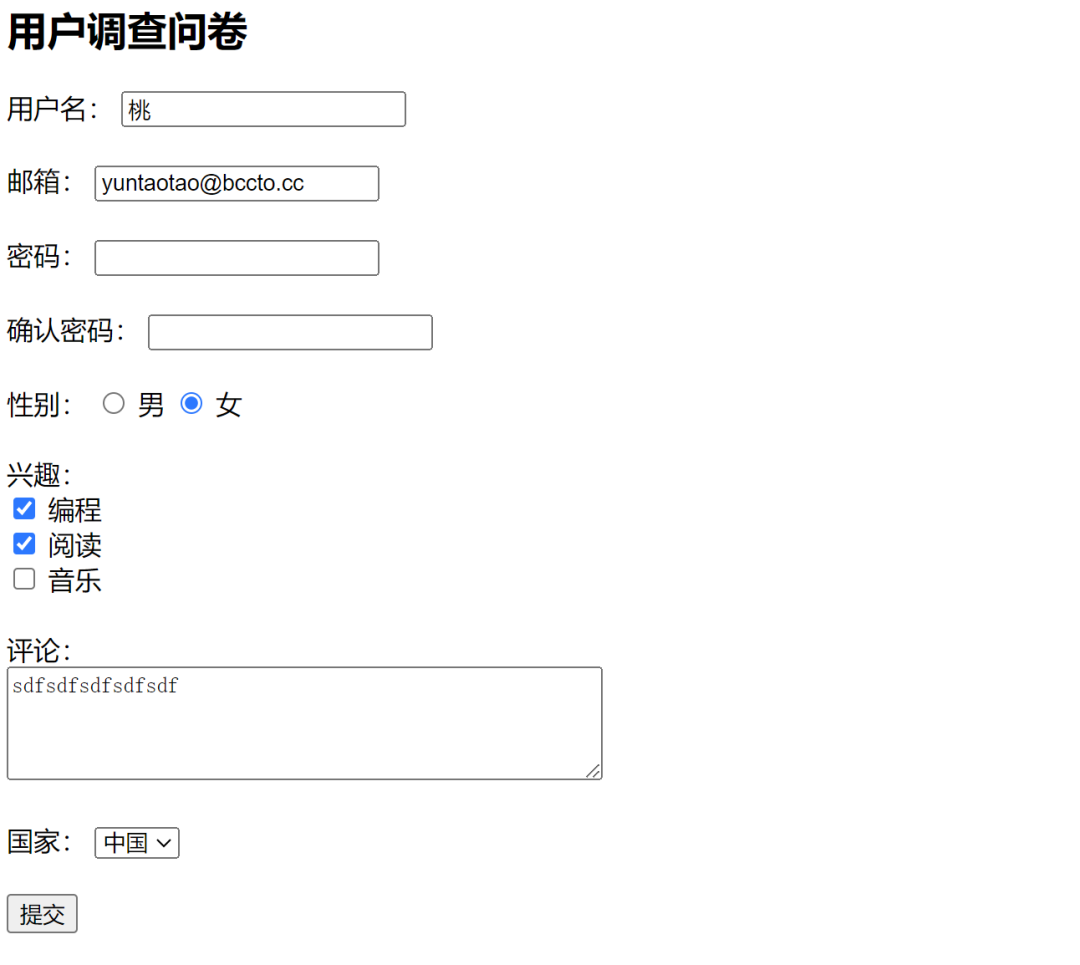
HTML基础:8个常见表单元素的详解
你好,我是云桃桃。 一个希望帮助更多朋友快速入门 WEB 前端程序媛。 后台回复“前端工具”可免费获取开发工具,持续更新。 今天来说说 HTML 表单。它是用于收集用户输入信息的元素集合。例如文本框、单选按钮、复选框、下拉列表等。 用户经常填写的表…...
密码学之哈希碰撞和生日悖论
哈希碰撞 哈希碰撞是指找到两个不一样的值,它们的哈希值却相同 假设哈希函数的取值空间大小为k ,计算次数为n 先算每个值不一样的概率P’ 所以至少两个值相同(即存在哈希碰撞)的概率P为 生日悖论 假设班里有50个人,求班里至少两个人相同…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...
