P8623 [蓝桥杯 2015 省 B] 移动距离 Python
[蓝桥杯 2015 省 B] 移动距离
题目描述
X 星球居民小区的楼房全是一样的,并且按矩阵样式排列。其楼房的编号为 $1,2,3, \cdots $ 。
当排满一行时,从下一行相邻的楼往反方向排号。
比如:当小区排号宽度为 6 6 6 时,开始情形如下:
1 2 3 4 5 6
12 11 10 9 8 7
13 14 15 .....
我们的问题是:已知了两个楼号 m m m 和 n n n,需要求出它们之间的最短移动距离。(不能斜线方向移动)
输入格式
输入为 3 3 3 个整数 w , m , n w,m,n w,m,n,空格分开,都在 1 1 1 到 10000 10000 10000 范围内。
w w w 为排号宽度, m , n m,n m,n 为待计算的楼号。
输出格式
要求输出一个整数,表示 m m m 与 n n n 两楼间最短移动距离。
样例 #1
样例输入 #1
6 8 2
样例输出 #1
4
样例 #2
样例输入 #2
4 7 20
样例输出 #2
5
提示
时限 1 秒, 256M。
蓝桥杯 2015 年省赛 B 组 H 题。
思路
先明白题意,其实就是找矩阵中怎么从一个点移动到另一个点,求总的步数。
再看下面这个图片,题目指定的楼号其实就是序号,如果按这样构造的矩阵,看 8 到 2 的距离的话**,
本质上是 8 的坐标 - 2 的坐标求和**
8(1,4) 2(0,1) (1-0) + (4-1)=4

这个肯定是二维数组,在二维数组中,每个元素都有自己的坐标,在给数组赋值时,其实就可以判断此时的序号是不是等于等会要判断的楼号,如果相等的话,就保存下坐标,当给定的两个坐标都知道时,就不必再继续赋值,直接退出循环,计算数值。
#创建一个w*10010的矩阵 ,每个位置为0
a = [[0]*w for i in range(10010)]
#在矩阵中,坐标的移动方向
dirction = [(0,1),(1,0),(0,-1),(1,0)]#右 下 左 下
#处理移动的逻辑 往右到头就去下面,往左到头继续往下走
while num<10001:#据题目知楼号在1-10000num+=1a[x][y] = numnewx = x + dirction[index][0]newy = y + dirction[index][1]if newx<0 or newy>=6 or newy <0:index = (index+1)%4newx = x + dirction[index][0]newy = yindex = (index +1)%4x = newxy = newy
#判断是否等于输入的楼号
if num == m:x1,y1 = x,yind_x1 = Trueif num == n:x2,y2 = x,yind_x2= Trueif ind_x1 ==True and ind_x2 ==True:break
总代码
import math
w,m,n = map(int,input().split())
a = [[0]*w for i in range(10010)]
num=0
x,y=0,0
index= 0
x1,y1=0,0
ind_x1,ind_x2 = False,False
dirction = [(0,1),(1,0),(0,-1),(1,0)]#右 下 左 下
while num<10001:num+=1a[x][y] = numif num == m:x1,y1 = x,yind_x1 = Trueif num == n:x2,y2 = x,yind_x2= Trueif ind_x1 ==True and ind_x2 ==True:breaknewx = x + dirction[index][0]newy = y + dirction[index][1]if newx<0 or newy>=w or newy <0:index = (index+1)%4# print("index_f",index)newx = x + dirction[index][0]newy = yindex = (index +1)%4# print("index_l",index)x = newxy = newy# print("value_x,value_y",x,y)
# for i in a:
# for num in i:
# print(f"{num:3d}",end="")
# print()
# print(x1,y1)
# print(x2,y2)
ans = abs(x1-x2) + abs (y1-y2)
print(ans)
相关文章:

P8623 [蓝桥杯 2015 省 B] 移动距离 Python
[蓝桥杯 2015 省 B] 移动距离 题目描述 X 星球居民小区的楼房全是一样的,并且按矩阵样式排列。其楼房的编号为 $1,2,3, \cdots $ 。 当排满一行时,从下一行相邻的楼往反方向排号。 比如:当小区排号宽度为 6 6 6 时,开始情形如…...
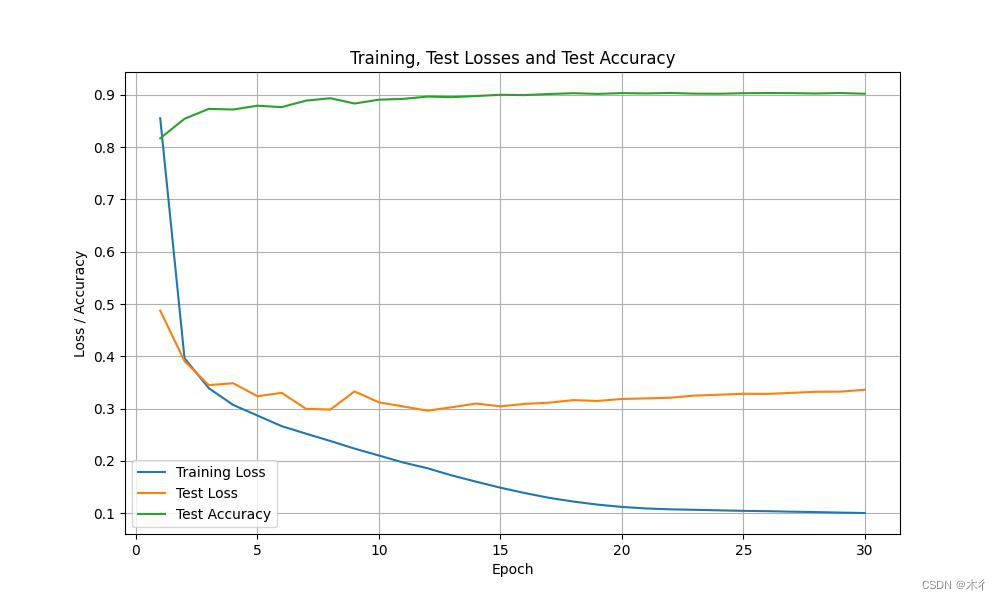
【Python】学习率调整策略详解和示例
学习率调整得当将有助于算法快速收敛和获取全局最优,以获得更好的性能。本文对学习率调度器进行示例介绍。 学习率调整的意义基础示例无学习率调整方法学习率调整方法一多因子调度器余弦调度器 结论 学习率调整的意义 首先,学习率的大小很重要。如果它…...

【Linux实践室】Linux用户管理实战指南:用户密码管理操作详解
🌈个人主页:聆风吟_ 🔥系列专栏:Linux实践室、网络奇遇记 🔖少年有梦不应止于心动,更要付诸行动。 文章目录 一. ⛳️任务描述二. ⛳️相关知识2.1 🔔用户密码存放地及方式2.2 🔔使用…...

UE5学习日记——蓝图节点前缀关键字整理
一、起因 节点如海,中英文翻译的时候还是有差别的,比如: 同一个中文,可能在英文里完全不同,连出现位置可能都不一样 附加 Attach Actor To Component(将Actor附加到组件)Append Array…...

浅析机器学习的常用方法
引言: 机器学习(Machine Learning,ML)是一种以计算机程序为基础,在不需要明确编程的情况下,对数据进行分析和处理的人工智能技术。与传统的计算机编程相比,机器学习的区别在于它通过数据建立模…...

大数据开发(日志离线分析项目)
大数据开发(日志离线分析项目) 一、项目需求1、使用jqueryecharts的方式调用程序后台提供的rest api接口,获取json数据,然后通过jquerycss的方式进行数据展示。工作流程如下:2、七大角度1、用户基本信息分析模块2、浏览…...
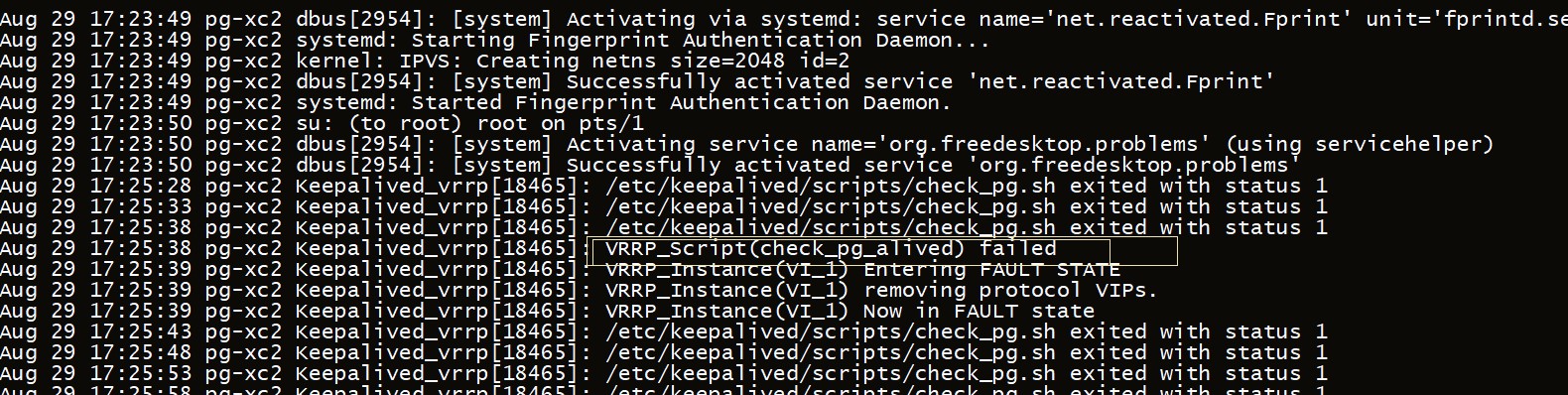
PostgreSQL技术大讲堂 - 第48讲:PG高可用实现keepalived
PostgreSQL从小白到专家,是从入门逐渐能力提升的一个系列教程,内容包括对PG基础的认知、包括安装使用、包括角色权限、包括维护管理、、等内容,希望对热爱PG、学习PG的同学们有帮助,欢迎持续关注CUUG PG技术大讲堂。 第48讲&#…...

【若依 SpringBoot 前后端分离版】修改加密传输后密码错误的解决方法(附排错过程)
目录 排错过程 报错信息 SysLoginController SysLoginService(问题核心) 太长不看版:解决方法 文章传送门:若依(RuoYi)SpringBoot框架密码加密传输(前后分离板)_若依密码加密方式-CSDN博客文章浏览阅读1.5w次,点赞…...
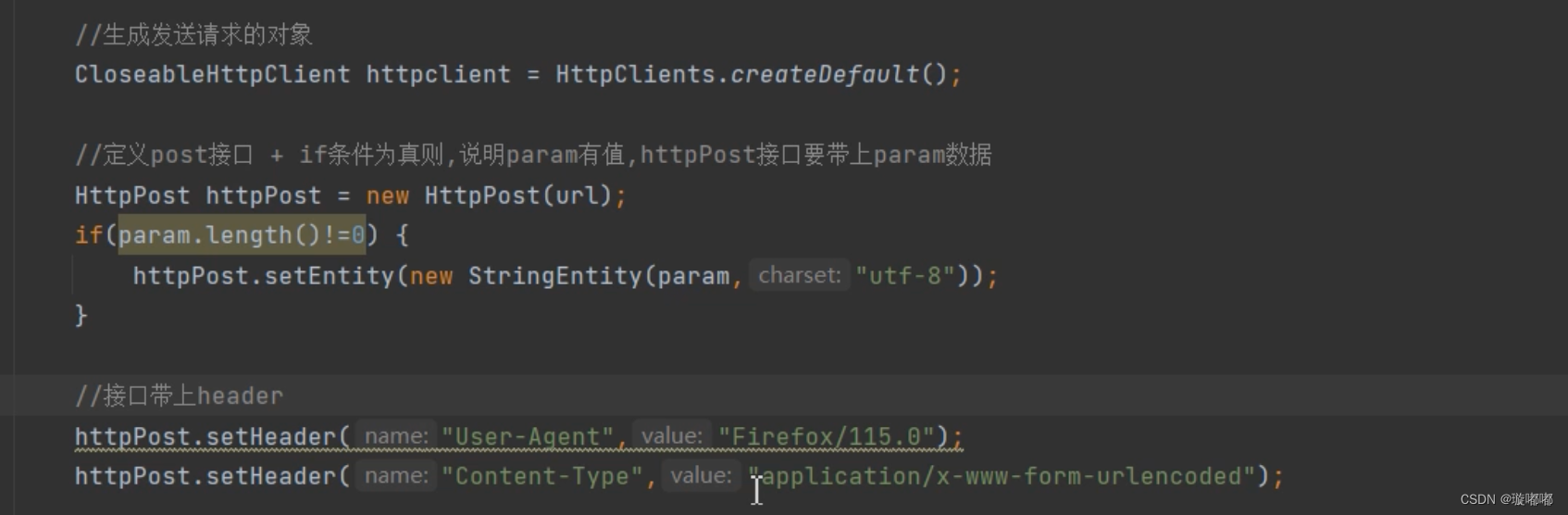
发送请求- header配置
请求头里是客户端的要求,把你的诉求告诉服务端,服务端按照你的要求返回数据 , 请求header需要严格全配置,把请求header全部传入,不能频繁访问,让后端知道它是正常请求 一般只配置User-Agent和Content Typ…...

C语言重难知识点
C语言重难知识点 if(a=1) 为真函数指针的调用(int)2.9 = 2逗号运算符,最右边表达式值作为整个逗号表达式的值。文件操作if(a=1) 为真 int a=0,b=0,c=0; if(a...

jMeter学习
一. JMeter介绍 1. 什么是JMeter? Apache JMeter™ 应用程序是开源软件,一个 100% 纯 Java 应用程序,旨在加载测试功能行为和测量性能 。它最初是为测试 Web 应用程序而设计的,但后来扩展到其他测试功能。 2. JMeter能做啥&#x…...

Nodejs运行vue项目时,报错:Error: error:0308010C:digital envelope routines::unsupported
前端项目使用( npm run dev ) 运行vue项目时,出现错误:Error: error:0308010C:digital envelope routines::unsupported 经过探索,发现问题所在,主要是nodeJs V17版本发布了OpenSSL3.0对算法和秘钥大小增加了更为严格的限制&#…...

华为汽车图谱
极狐 极狐(ARCFOX)是由北汽、华为、戴姆勒、麦格纳等联合打造。总部位于北京蓝谷。 问界 华为与赛力斯(东风小康)合作的成果。 阿维塔 阿维塔(AVATR)是由长安汽车、华为、宁德时代三方联合打造。公司总部位…...

鸿蒙操作系统-初识
HarmonyOS-初识 简述安装配置hello world1.创建项目2.目录解释3.构建页面4.真机运行 应用程序包共享包HARHSP 快速修复包 官方文档请参考:HarmonyOS 简述 1.定义:HarmonyOS是分布式操作系统,它旨在为不同类型的智能设备提供统一的操作系统&a…...
)
【ZZULIOJ】1003: 两个整数的四则运算(Java)
题目描述 输入两个整数num1和num2,请你设计一个程序,计算并输出它们的和、差、积、整数商及余数。 输入 输入只有两个正整数num1、num2。 输出 输出占一行,包括两个数的和、差、积、商及余数,数据之间用一个空格隔开。 样例…...

聊聊芯片原厂
芯片原厂是芯片的生产商,他们制造和设计芯片,并拥有产品的所有权原厂这个词是为了区分芯片代理商(厂)而创造的。 每一家芯片制造商都会通过自己忠诚的芯片代理商(厂)来销售自己的芯片,代理商(厂)也会打着芯片制造商的旗号来销售芯片,因此有时候为了强调自己的正统地…...
百人一岗,Android开发者的困境。。。。。
前言 在当前的Android开发领域,竞争的激烈程度已经达到了前所未有的水平,几乎到了100个开发者竞争1个岗位的地步。 这种“内卷”现象的背后,是技术的快速发展和市场对Android开发者技能要求的不断提升。随着移动应用的普及和多样化…...

若依分离版 —引入echart连接Springboot后端
1. vue引入echart (1)首先安装ECharts库。可以通过npm npm install echarts --save (2)在vue页面中添加一个容器元素来显示图表 <el-card class"mt20"><div id"ha" ref"main"><…...

Halcon深度学习项目实战
Halcon在机器视觉中的价值主要体现在提供高效、可扩展、灵活的机器视觉解决方案,帮助用户解决各种复杂的机器视觉问题,提高生产效率和产品质量。 缩短产品上市时间 Halcon的灵活架构使其能够快速开发出任何类型的机器视觉应用。其全球通用的集成开发环…...

子类中的方法去调用父类中的方法有几种形式?原生django如何向响应头写入数据
1 子类中的方法去调用父类中的方法有几种形式 2 原生django如何向响应头写入数据 1 子类中的方法去调用父类中的方法有几种形式? class Animal:def eat(self):print(self.name, 在吃饭)class Dog(Animal):def __init__(self, name):self.name namedef test(self):#…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林:一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好,未来的算法大神! 在数据结构的世界里,“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的,它…...

前端调试HTTP状态码
1xx(信息类状态码) 这类状态码表示临时响应,需要客户端继续处理请求。 100 Continue 服务器已收到请求的初始部分,客户端应继续发送剩余部分。 2xx(成功类状态码) 表示请求已成功被服务器接收、理解并处…...
如何做好一份技术文档?从规划到实践的完整指南
如何做好一份技术文档?从规划到实践的完整指南 🌟 嗨,我是IRpickstars! 🌌 总有一行代码,能点亮万千星辰。 🔍 在技术的宇宙中,我愿做永不停歇的探索者。 ✨ 用代码丈量世界&…...
