LeetCode刷题--- 等差数列划分 II - 子序列
个人主页:元清加油_【C++】,【C语言】,【数据结构与算法】-CSDN博客
个人专栏
力扣递归题
http://t.csdnimg.cn/yUl2I
【C++】
http://t.csdnimg.cn/6AbpV
数据结构
http://t.csdnimg.cn/hKh2l
前言:这个专栏主要讲述动态规划算法,所以下面题目主要也是这些算法做的
我讲述题目会把讲解部分分为3个部分:
1、题目解析
2、算法原理思路讲解
3、代码实现
等差数列划分 II - 子序列
题目链接:等差数列划分 II - 子序列
题目
给你一个整数数组 nums ,返回 nums 中所有 等差子序列 的数目。
如果一个序列中 至少有三个元素 ,并且任意两个相邻元素之差相同,则称该序列为等差序列。
- 例如,
[1, 3, 5, 7, 9]、[7, 7, 7, 7]和[3, -1, -5, -9]都是等差序列。 - 再例如,
[1, 1, 2, 5, 7]不是等差序列。
数组中的子序列是从数组中删除一些元素(也可能不删除)得到的一个序列。
- 例如,
[2,5,10]是[1,2,1,2,4,1,5,10]的一个子序列。
题目数据保证答案是一个 32-bit 整数。
示例 1:
输入:nums = [2,4,6,8,10] 输出:7 解释:所有的等差子序列为: [2,4,6] [4,6,8] [6,8,10] [2,4,6,8] [4,6,8,10] [2,4,6,8,10] [2,6,10]
示例 2:
输入:nums = [7,7,7,7,7] 输出:16 解释:数组中的任意子序列都是等差子序列。
提示:
1 <= nums.length <= 1000-231 <= nums[i] <= 231 - 1
解法
算法原理与解析
我们这题使用动态规划,我们做这类题目可以分为以下五个步骤
- 状态显示
- 状态转移方程
- 初始化(防止填表时不越界)
- 填表顺序
- 返回值
- 状态显示
- 状态转移方程
- a 存在,下标为 k ,并且 a < b :此时我们知道以 k 元素以及 i 元素结尾的等差序列的个数 dp[k][i] ,在这些⼦序列的后⾯加上 j 位置的元素依旧是等差序列。但是这⾥会多出来⼀个以 k, i, j 位置的元素组成的新的等差序列,因此 dp[i][j] = dp[k][i] + 1 ;
- 因为 a 可能有很多个,我们需要全部累加起来。
- 初始化(防止填表时不越界)
- 填表顺序
- 先固定倒数第⼀个数;
- 然后枚举倒数第⼆个数。
- 返回值
代码实现
class Solution {
public:
typedef long long ll;int numberOfArithmeticSlices(vector<int>& nums) {int n = nums.size();// 优化unordered_map<ll, vector<int>> hash;for (int i = 0; i < n; i++){hash[nums[i]].push_back(i);}vector<vector<int>> dp(n, vector<int>(n)); // 创建 dp 表int sum = 0;for (int j = 2; j < n; j++) // 固定倒数第一个数{for (int i = 1; i < j; i++) // 枚举倒数第二个数{ll a = (ll)nums[i] * 2 - nums[j]; // 处理数据溢出if (hash.count(a)){for (auto k : hash[a]){if (k < i){dp[i][j] += dp[k][i] + 1;}else break;}}sum += dp[i][j];}}return sum;}
};相关文章:

LeetCode刷题--- 等差数列划分 II - 子序列
个人主页:元清加油_【C】,【C语言】,【数据结构与算法】-CSDN博客 个人专栏 力扣递归题 http://t.csdnimg.cn/yUl2I 【C】 http://t.csdnimg.cn/6AbpV 数据结构 http://t.csdnimg.cn/hKh2l 前言:这个专栏主要讲述动态规划算…...
kubectl 启用shell自动补全功能
官网手册参考:https://kubernetes.io/zh-cn/docs/tasks/tools/install-kubectl-linux/ 系统:centos7 补全脚本依赖于工具 bash-completion, 所以要先安装它(可以用命令 type _init_completion 检查 bash-completion 是否已安装&a…...
极简wordpress网站模板
Pithy设计师wordpress网站模板 精练简洁的wordpress模板,设计师或设计工作室展示型网站模板。 https://www.jianzhanpress.com/?p6329...
python的字典dict按照key或value排序的不同方法)
【python】(16)python的字典dict按照key或value排序的不同方法
系列文章回顾 【python】(01)初识装饰器Decorator 【python】(02)初识迭代器Iterator 【python】(03)初识生成器Generator 【python】(04)python中实现多任务并发和并行的区别 【python】(05)如何使用python中的logging模块记录日志信息 【python】(06)理解Python中的 lambda 、…...
_VI 深入理解Zuul服务网关)
微服务篇-C 深入理解第一代微服务(SpringCloud)_VI 深入理解Zuul服务网关
原创作者:田超凡(程序员田宝宝) 版权所有,引用请注明原作者,严禁复制转载 Part 1 理论部分 1 网关类别有哪些? 常见的网关类别有三种:开放API(Open API)网关、微服务…...
web CSS笔记1
CSS(Cascading Style Sheets) 美化样式 CSS通常称为CSS样式表或层叠样式表(级联样式表),主要用于设置HTML页面中的文本内容(字体、大小、对齐方式等)、图片的外形(宽高、边框样式、边距等)以及…...

js算法记录
> 更多请前往 https://www.passerma.com/article/86 滑动窗口 1 给定一个矩阵,包含N*M个整数,和一个包含K个整数的数组。现在要求在这个矩阵中找一个宽度最小的子矩阵,要求子矩阵包含数组中所有的整数 function minSubmatrixWidth(mat…...

球面数据的几何深度学习--球形 CNN
目录 一、说明二、球形 CNN概述三、球面数据的对称性四、标准(平面)CNN的局限性五、卷积并发症六、球面卷积七、球面卷积是不够的 一、说明 球面数据的几何深度学习–球形 CNN。通过对物理世界的平移对称性进行编码,卷积神经网络 ࿰…...
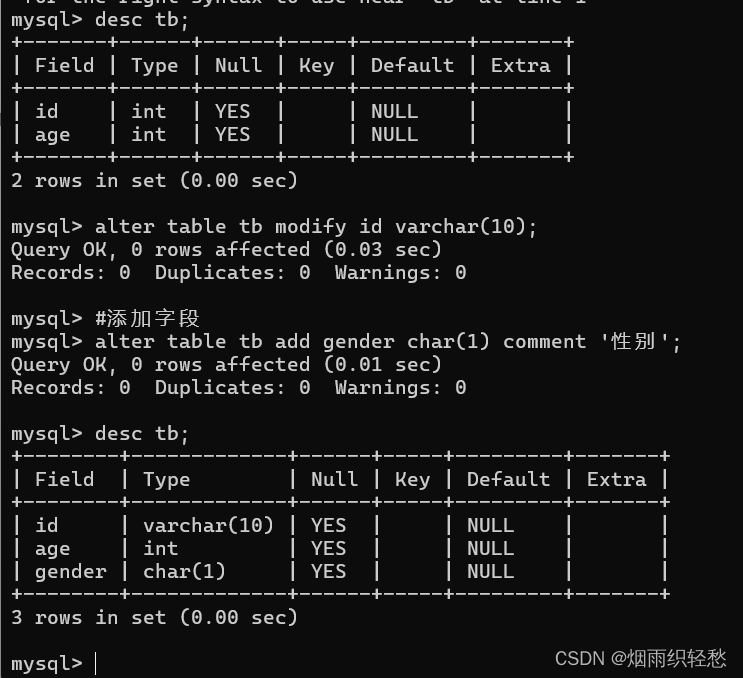
MySQL学习笔记------SQL(1)
关系型数据库(RDBMS) 建立在关系模型基础上,由多张相互连接的二维表组成的数据库 特点:使用表储存数据,格式统一,便于维护 使用SQL语言操作,标准统一,使用方便 SQL通用语法 SQL…...

PMP能提前查成绩?还能改分数?别太离谱!
震惊!3月10日PMP考试才结束没多久,昨天就有学员收到了查分邮件,寄信人自称自己是内部人员,可以提前查询到成绩并直接修改成绩。 这也太离谱了吧!在此,小赛想说,PMP考试是一个公正、严格的考试体…...

【保姆级讲解服务器硬件的基础知识】
服务器硬件基础知识 1. 前言2. 中央处理器(CPU)3. 内存(RAM)4. 存储设备5. 主板6. 电源供应单元(PSU)7. 冷却系统8. 网络连接9. 扩展插槽和端口10. 管理功能 🌈🌈🌈&…...

并查集---力扣547省份的数量
假设:有一群小混混打架,小弟们可能互相不认识,如果要确定他们是一伙的,就需要确定他们的组长是不是一个,但是每个组长的领导可能又不一样,所以要找到最大的那个领导,才能确定是一伙的。 我们先…...
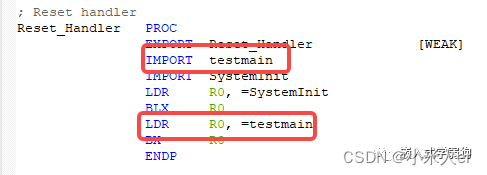
stm32启动文件里面的__main和主函数main()
一、__main和main()之间的关系 先来对stm32启动过程简单学习 启动文件里面的Reset_Handler: 调用过程: stm32在启动后先进入重启中断函数Reset_Handler,其中会先后调用SystemInit和__main函数, __main函数属于c库函数&…...

曲线生成 | 图解Reeds-Shepp曲线生成原理(附ROS C++/Python/Matlab仿真)
目录 0 专栏介绍1 什么是Reeds-Shepp曲线?2 Reeds-Shepp曲线的运动模式3 Reeds-Shepp曲线算法原理3.1 坐标变换3.2 时间翻转(time-flip)3.3 反射变换(reflect)3.4 后向变换(backwards) 4 仿真实现4.1 ROS C实现4.2 Python实现4.3 Matlab实现 0 专栏介绍 ǵ…...
深入探讨iOS开发:从创建第一个iOS程序到纯代码实现全面解析
iOS开发作为移动应用开发的重要领域之一,对于开发人员具有重要意义。本文将深入探讨iOS开发的各个方面,从创建第一个iOS程序到纯代码实现iOS开发,带领读者全面了解iOS应用程序的开发流程和技术要点。 📱 第一个iOS程序 在创建第…...

Python学习之-正则表达式
目录 前言:1.re.serach1.1例子: 2.re.match2.1示例1:2.2 示例2: 3.re.findall3.1 示例 4.re.fullmatch4.1 示例1:4.2 示例2: 5.re.split5.1 示例1:5.2 示例2:5.3 示例3: 6.re.sub6.1 示例&#…...
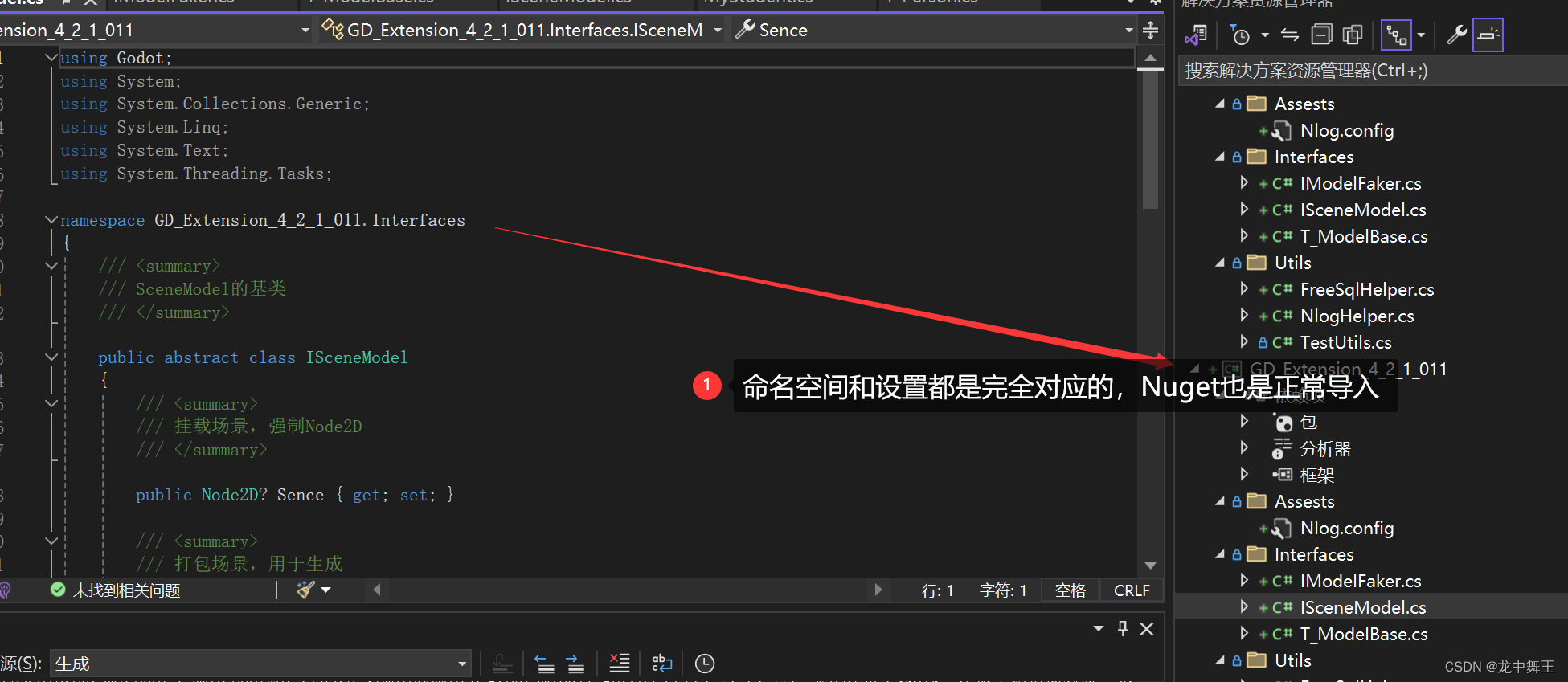
Godot.NET C# 工程化开发(1):通用Nuget 导入+ 模板文件导出,包含随机数生成,日志管理,数据库连接等功能
文章目录 前言Github项目地址,包含模板文件后期思考补充项目设置编写失误环境visual studio 配置详细的配置看我这篇文章 Nuget 推荐NewtonSoft 成功Bogus 成功Github文档地址随机生成构造器生成构造器接口(推荐) 文件夹设置Nlog 成功!Nlog.configNlogHe…...

数据仓库——雪花模式以及层次递归
层次结构 钻取 向下钻取:对某些代表事实的报表中添加维度细节 向上钻取:从某些代表事实的报表中去除维度细节 属性层次 提供了一种自然方法,用于顺序地在不断深入的层次上组织事实。许多维度可以被理解为包含连续主从关系的属性层次。此类…...
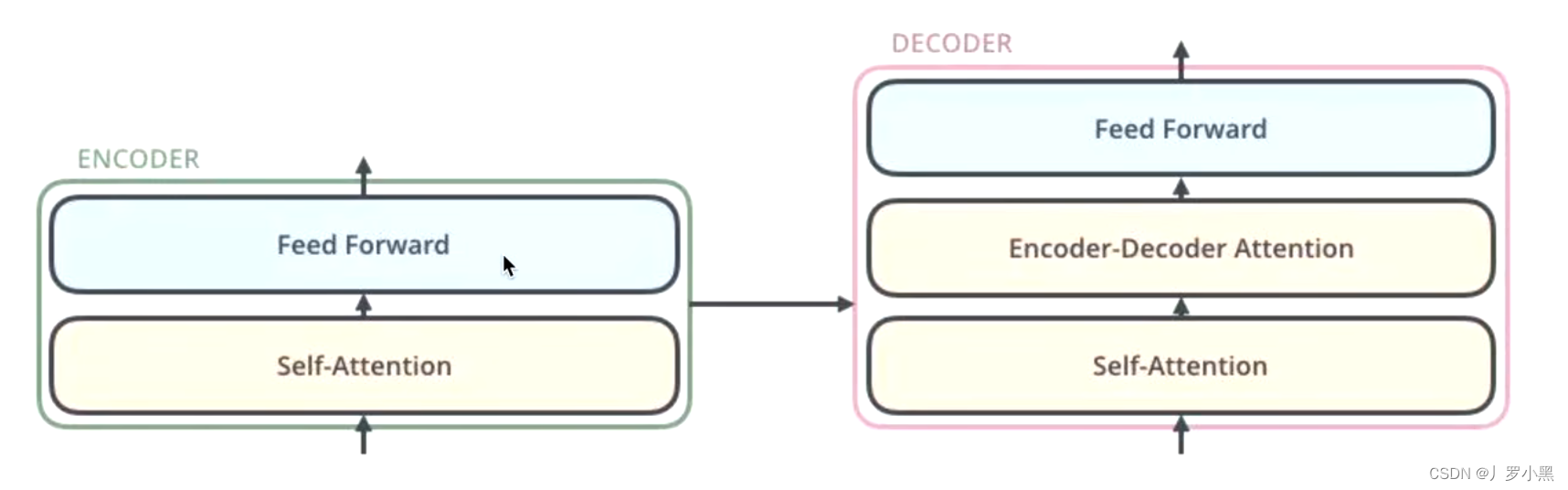
Transformer的前世今生 day09(Transformer的框架概述)
前情提要 编码器-解码器结构 如果将一个模型分为两块:编码器和解码器那么编码器-解码器结构为:编码器负责处理输入,解码器负责生成输出流程:我们先将输入送入编码器层,得到一个中间状态state,并送入解码器…...
Qt 压缩/解压文件
前面讲了很多Qt的文件操作,文件操作自然就包括压缩与解压缩文件了,正好最近项目里要用到压缩以及解压缩文件,所以就研究了一下Qt如何压缩与解压缩文件。 QZipReader/QZipWriter QZipReader 和 QZipWriter 类提供了用于读取和写入 ZIP 格式文…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...

提升移动端网页调试效率:WebDebugX 与常见工具组合实践
在日常移动端开发中,网页调试始终是一个高频但又极具挑战的环节。尤其在面对 iOS 与 Android 的混合技术栈、各种设备差异化行为时,开发者迫切需要一套高效、可靠且跨平台的调试方案。过去,我们或多或少使用过 Chrome DevTools、Remote Debug…...

Mysql故障排插与环境优化
前置知识点 最上层是一些客户端和连接服务,包含本 sock 通信和大多数jiyukehuduan/服务端工具实现的TCP/IP通信。主要完成一些简介处理、授权认证、及相关的安全方案等。在该层上引入了线程池的概念,为通过安全认证接入的客户端提供线程。同样在该层上可…...

使用 uv 工具快速部署并管理 vLLM 推理环境
uv:现代 Python 项目管理的高效助手 uv:Rust 驱动的 Python 包管理新时代 在部署大语言模型(LLM)推理服务时,vLLM 是一个备受关注的方案,具备高吞吐、低延迟和对 OpenAI API 的良好兼容性。为了提高部署效…...

android 之 KeyguardService
一、功能定位与核心作用 KeyguardService 是 Android 锁屏功能的核心服务,负责管理设备锁屏界面(如密码、图案、指纹等验证流程),并协调系统安全策略与用户交互。主要职责包括: 锁屏状态管理 控制锁屏界面的显示/隐藏…...
