798.差分矩阵
输入一个 n行 m列的整数矩阵,再输入 q个操作,每个操作包含五个整数 x1,y1,x2,y2,c,其中 (x1,y1)和 (x2,y2)
表示一个子矩阵的左上角坐标和右下角坐标。每个操作都要将选中的子矩阵中的每个元素的值加上 c。
请你将进行完所有操作后的矩阵输出。
输入格式
第一行包含整数 n,m,q。
接下来 n行,每行包含 m个整数,表示整数矩阵。
接下来 q行,每行包含 5个整数 x1,y1,x2,y2,c,表示一个操作。
输出格式
共 n行,每行 m个整数,表示所有操作进行完毕后的最终矩阵。
数据范围
1≤n,m≤1000,
1≤q≤100000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤c≤1000,
−1000≤矩阵内元素的值≤1000
输入样例:
3 4 3
1 2 2 1
3 2 2 1
1 1 1 1
1 1 2 2 1
1 3 2 3 2
3 1 3 4 1
输出样例:
2 3 4 1
4 3 4 1
2 2 2 2
#include<bits/stdc++.h>
using namespace std;
const int N = 1010;int n, m, q;
int a[N][N], b[N][N];void insert(int x1, int y1, int x2, int y2, int c) {b[x1][y1] += c;b[x2 + 1][y1] -= c;b[x1][y2 + 1] -= c;b[x2 + 1][y2 + 1] += c;
}int main() {cin >> n >> m >> q;for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++)cin >> a[i][j];}for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {insert(i, j, i, j, a[i][j]);}}while (q--) {int x1, y1, x2, y2, c;cin >> x1 >> y1 >> x2 >> y2 >> c;insert(x1, y1, x2, y2, c);}for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];}}for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {cout << b[i][j] << " ";}cout << endl;}return 0;
}
相关文章:

798.差分矩阵
输入一个 n行 m列的整数矩阵,再输入 q个操作,每个操作包含五个整数 x1,y1,x2,y2,c,其中 (x1,y1)和 (x2,y2) 表示一个子矩阵的左上角坐标和右下角坐标。每个操作都要将选中的子矩阵中的每个元素的值加上 c。 请你将进行完所有操作后的矩阵输出…...

InfluxDB 2 介绍与使用 flux查询 数据可视化
一、关键概念 相比V1 移除了database 和 RP,增加了bucket。 V2具有以下几个概念: timestamp、field key、field value、field set、tag key、tag value、tag set、measurement、series、point、bucket、bucket schema、organization 新增的概念&…...
Qt QTreeView简单使用
QT-QTreeView使用方法 QTreeView: 用于显示树状结构数据,适用于树状结构数据的操作。 一、初始化 利用QStandardlternModel来初始化数据,标准的基于项数据的数据模型类, 每个项数据可以是任何数据类型。 // 初始化model QStandardItem…...
Wannacrypt蠕虫老树开花?又见Wannacrypt
Wannacrypt蠕虫是一个在2017年就出现的远古毒株,其利用永恒之蓝漏洞降维打击用户服务器,而后进行扩散勒索,曾经一度风靡全球,可谓是闻者伤心,听着落泪,因为这玩意解密是不可能 解密的。 而2023年的今天&am…...
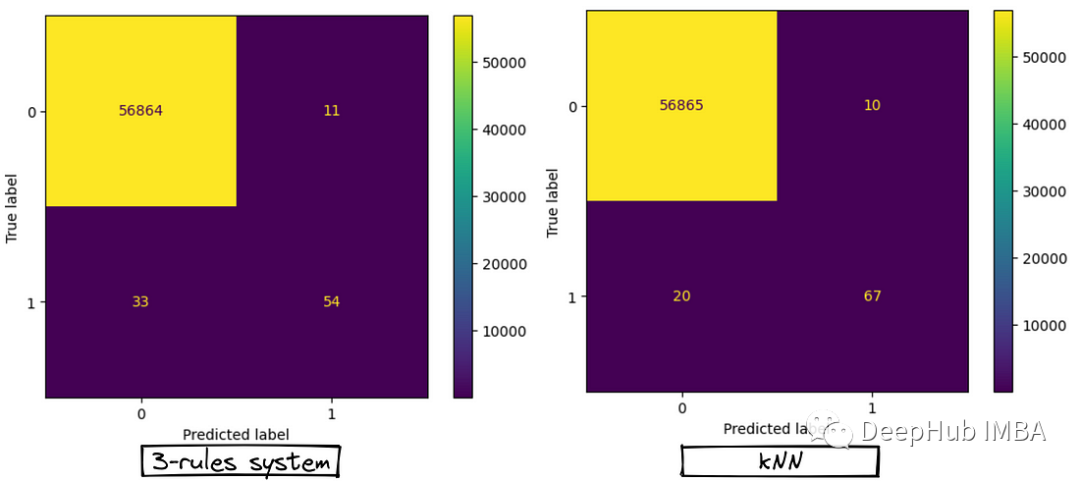
结合基于规则和机器学习的方法构建强大的混合系统
经过这些年的发展,我们都确信ML即使不能表现得更好,至少也可以在几乎所有地方与前ML时代的解决方案相匹配。比如说一些规则约束,我们都会想到能否把它们替换为基于树的ml模型。但是世界并不总是黑白分明的,虽然机器学习在解决问题…...
Spring Security OAuth2实现多用户类型认证、刷新Token
原本的OAuth2登录支持用户名密码登录,现在还想支持另外用id号码和密码登录。但是OAuth2默认提供的UserDetailsService只允许传入一个参数:想要实现多种用户登录,是不是可以考虑loadUserByUsername方法携带多个参数呢?接下来记录一…...

云计算介绍,让你更了解云计算
同学们好! 第一次接触IT行业吗?没关系,看完这篇文章肯定会让你不再陌生。给自己几分钟时间,认真看完哦! 1、不知道什么是云计算? 网络计算云计算 官方定义是:通过网络提供可伸缩的分布式计算…...

阿里大佬翻遍全网Java面试文章,总结出这份1658页文档,GitHub收获25K+点赞
就目前大环境来看,跳槽成功的难度比往年高很多。一个明显的感受:今年的面试,无论一面还是二面,都很考验Java程序员的技术功底。这不又到了面试跳槽的黄金段,成功升职加薪,不成功饱受打击。当然也要注意&…...

【JDK1.8 新特性】Lambda表达式
1. 什么是Lambda表达式? Lambda 是一个匿名函数,我们可以把 Lambda 表达式理解为是一段可以传递的代码(将代码像数据一样进行传递)。使用它可以写出更简洁、更灵活的代码。作为一种更紧凑的代码风格,使Java的语言表达…...

【Vue.js】Vuex核心概念
文章目录全局状态管理模式Vuexvuex是什么?什么是“状态管理模式”?vuex的应用场景Vuex安装开始核心概念一、State1、单一状态树2、在 Vue 组件中获得 Vuex 状态3、mapState辅助函数二、Getter三、Mutation1、提交载荷(Payload)2、…...

react router零基础使用教程
安装既然学习 react router 就免不了运行 react安装 reactnpx create-react-app my-appcd my-appnpm start安装 react routernpm install react-router-dom如果一切正常,就让我们打开 index.js 文件。配置路由引入 react-router-dom 的 RouterProviderimport {Route…...

IOC三种依赖注入的方式,以及区别
目录构造方法注入(constructor injection)setter 方法注入(setter injection)接口注入(interface injection)三种方式比较构造方法注入(constructor injection) 构造方法中声明依赖…...
Ubuntu18安装新版本PCL-1.13,并和ROS自带PCL-1.8共存
文章目录1.安装新版本PCL-1.132.在工程中使用新版本的PCL-1.133.pcl-1.13误装到/usr/local/下如何卸载1.安装新版本PCL-1.13 下载PCL-1.13代码: 修改CMakeLists.txt文件,不编译vtk相关的代码:vtk的问题比较难解决,但是一般我们安…...
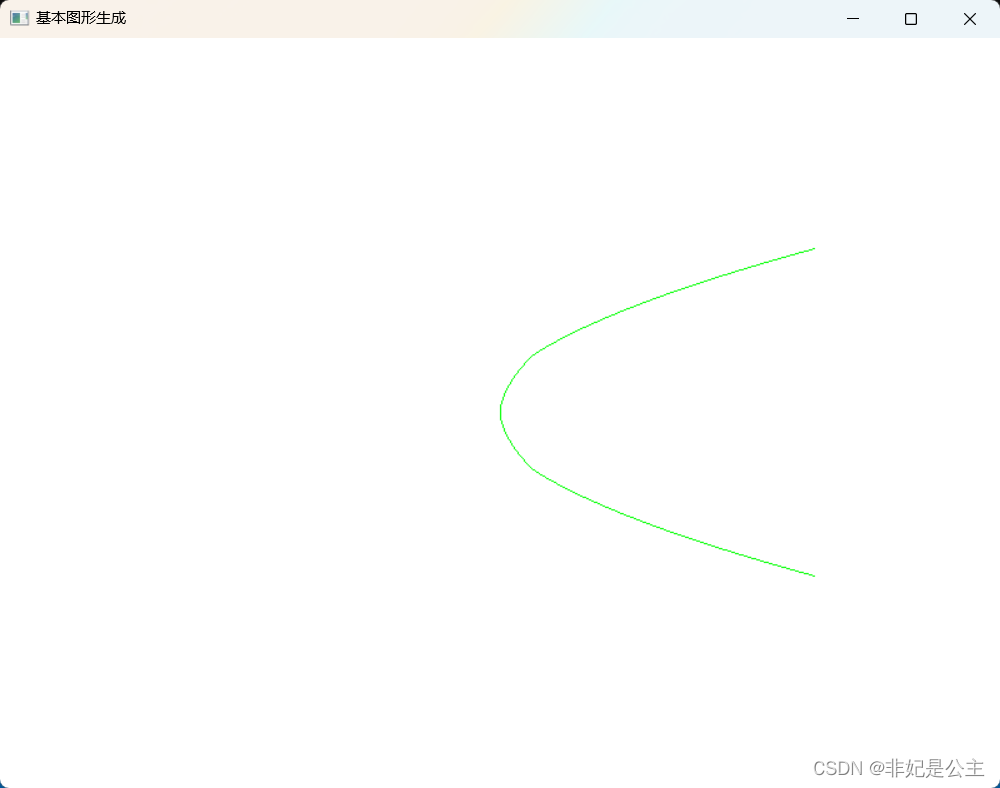
计算机图形学08:中点BH算法绘制抛物线(100x = y^2)
作者:非妃是公主 专栏:《计算机图形学》 博客地址:https://blog.csdn.net/myf_666 个性签:顺境不惰,逆境不馁,以心制境,万事可成。——曾国藩 文章目录专栏推荐专栏系列文章序一、算法原理二、…...
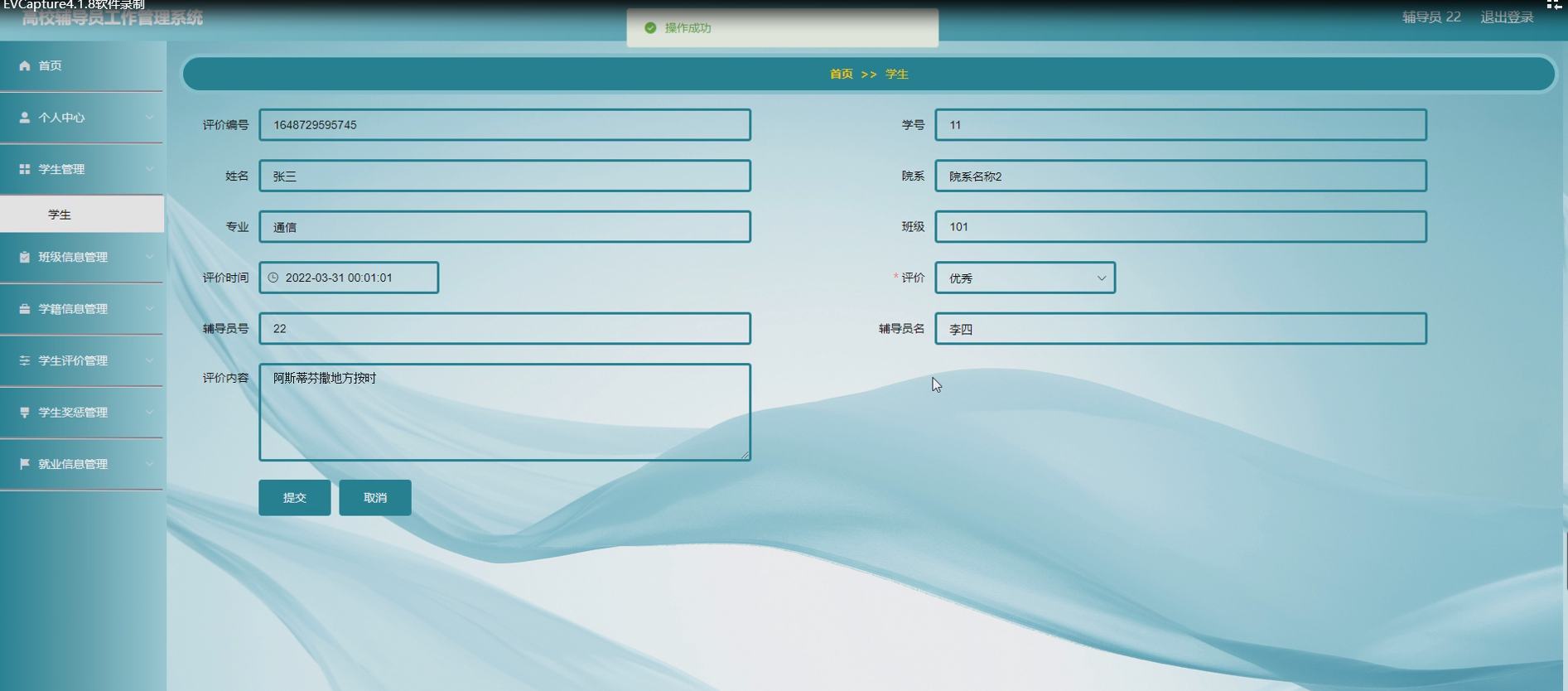
基于java的高校辅导员工作管理系统
摘 要网络技术的快速发展给各行各业带来了很大的突破,也给各行各业提供了一种新的管理模块,对于高校辅导员工作管理将是又一个传统管理到智能化信息管理的改革,设计高校辅导员工作管理系统的目的就是借助计算机让复杂的班级信息、学籍信息等管…...
字节3次都没裁掉的7年老测试。掌握设计业务与技术方案,打开上升通道!
前言职场中的那些魔幻操作,研发最烦的是哪个?“面对业务需求的时候,可能都听过这样一句话:这个很简单,直接开发,三天内上线;”朋友说:“产品听了流泪,测试见了崩溃&#…...
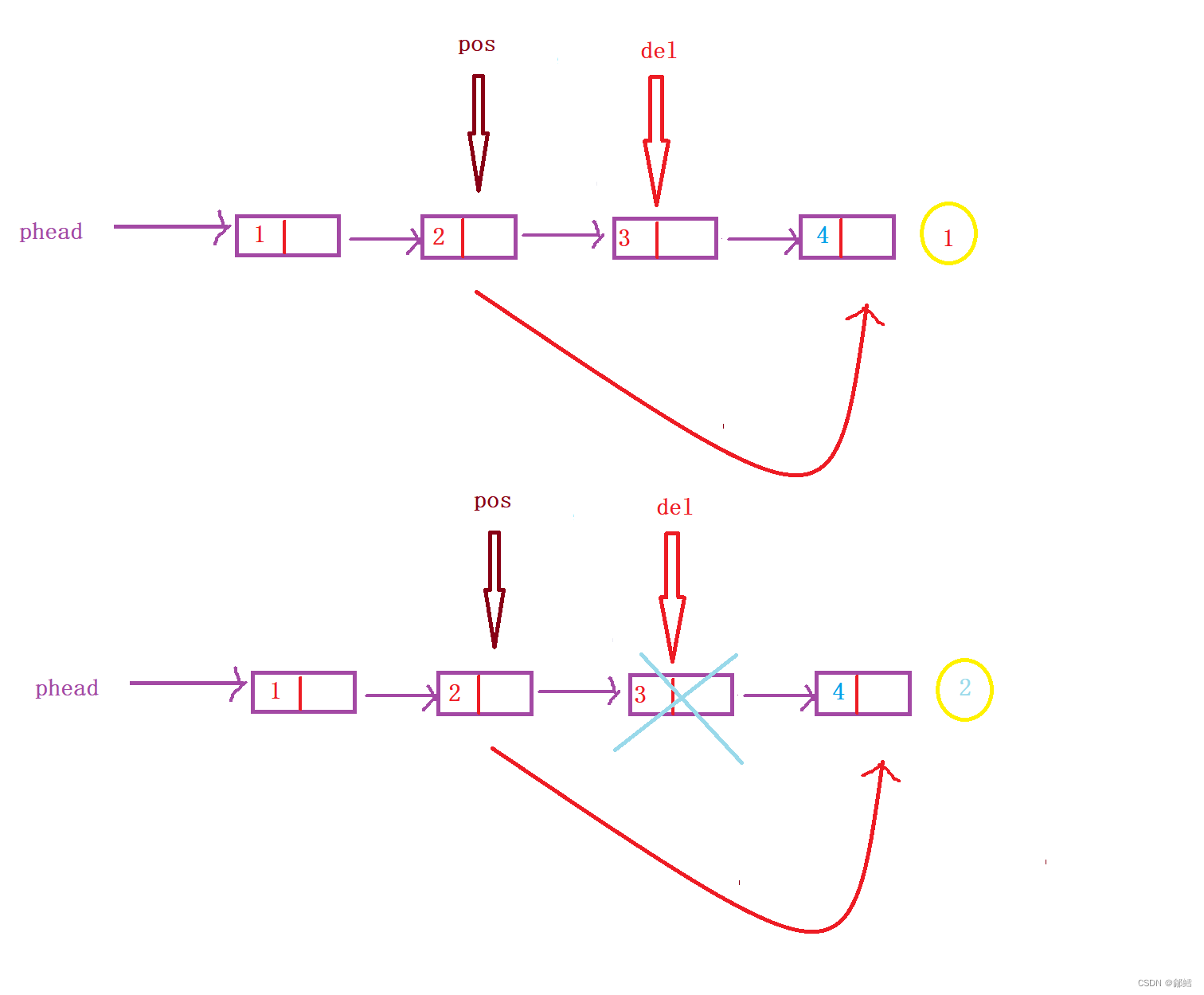
详细介绍关于链表【数据结构】
文章目录链表单链表尾插头插尾删第一种方式删除第二种头删查找pos之前插入pos位置删除pos后面插入pos位置后面删除链表 顺序表缺点: 空间不够了 需要扩容,但是扩容是有消耗的头部或中间位置需要插入或删除,需要挪动 ,但是挪动是…...

2.3 二分搜索技术
二分搜索算法是运用分治策略的典型例子。给定己排好府的 n个元素a10:n-1],现要在这n个元素中找出一特定元素3。首先较容易想到的是用顺序搜索方法,逐个比较a10:1-1]中元素,直至找出元素,或搜索遍整个数组后确定,不在其…...
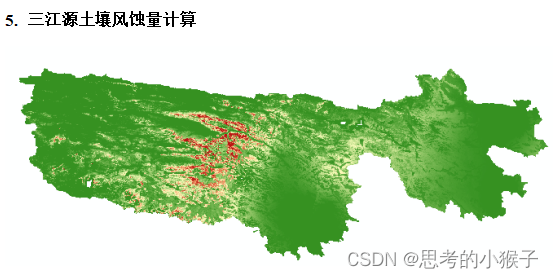
RWEQ模型的土壤风蚀模数估算、其变化归因分析
土壤风蚀是一个全球性的环境问题。中国是世界上受土壤风蚀危害最严重的国家之一,土壤风蚀是中国干旱、半干旱及部分湿润地区土地荒漠化的首要过程。中国风蚀荒漠化面积达160.74104km2,占国土总面积的16.7%,严重影响这些地区的资源开发和社会经…...
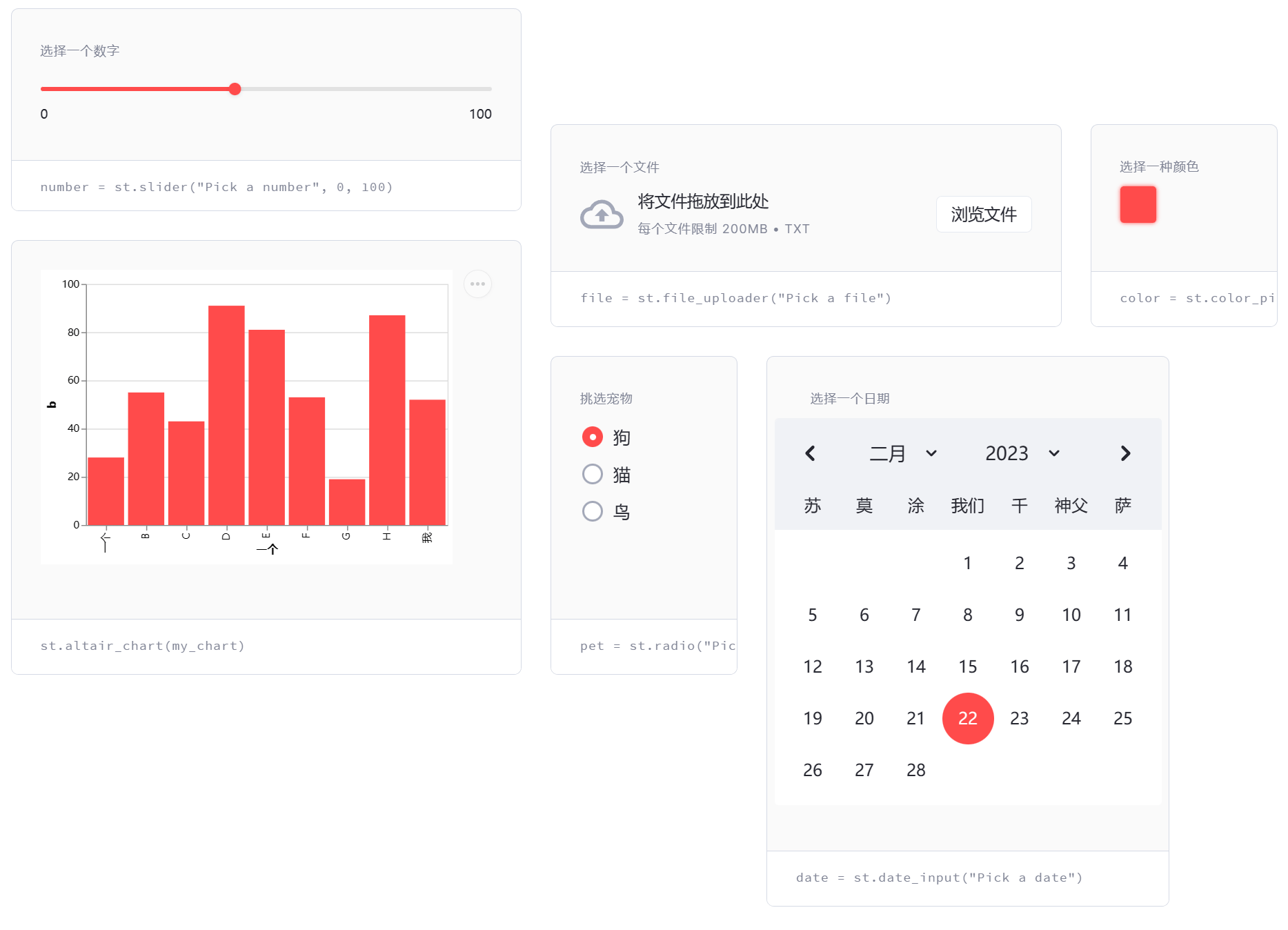
学习streamlit-1
Streamlit A faster way to build and share data apps streamlit在几分钟内就可以将数据脚本转换为可共享的web应用程序,并且是纯python编程,无需前端经验。 快速开始 streamlit非常容易上手,运行demo只需2行代码: pip install…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...
)
Leetcode33( 搜索旋转排序数组)
题目表述 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nu…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...

【HarmonyOS 5】鸿蒙中Stage模型与FA模型详解
一、前言 在HarmonyOS 5的应用开发模型中,featureAbility是旧版FA模型(Feature Ability)的用法,Stage模型已采用全新的应用架构,推荐使用组件化的上下文获取方式,而非依赖featureAbility。 FA大概是API7之…...

针对药品仓库的效期管理问题,如何利用WMS系统“破局”
案例: 某医药分销企业,主要经营各类药品的批发与零售。由于药品的特殊性,效期管理至关重要,但该企业一直面临效期问题的困扰。在未使用WMS系统之前,其药品入库、存储、出库等环节的效期管理主要依赖人工记录与检查。库…...

倒装芯片凸点成型工艺
UBM(Under Bump Metallization)与Bump(焊球)形成工艺流程。我们可以将整张流程图分为三大阶段来理解: 🔧 一、UBM(Under Bump Metallization)工艺流程(黄色区域ÿ…...

基于Uniapp的HarmonyOS 5.0体育应用开发攻略
一、技术架构设计 1.混合开发框架选型 (1)使用Uniapp 3.8版本支持ArkTS编译 (2)通过uni-harmony插件调用原生能力 (3)分层架构设计: graph TDA[UI层] -->|Vue语法| B(Uniapp框架)B --&g…...
