蓝桥杯 - 小明的背包1(01背包)


解题思路:
本题属于01背包问题,使用动态规划
dp[ j ]表示容量为 j 的背包的最大价值
注意:
需要时刻提醒自己dp[ j ]代表的含义,不然容易晕头转向
注意越界问题,且 j 需要倒序遍历
如果正序遍历
dp[1] = dp[1 - volume[0]] + value[0] = 15
dp[2] = dp[2 - volume[0]] + value[0] = 30
此时dp[2]就已经是30了,意味着物品0,被放入了两次,所以不能正序遍历。
为什么倒叙遍历,就可以保证物品只放入一次呢?
倒叙就是先算dp[2]
dp[2] = dp[2 - volume[0]] + value[0] = 15 (dp数组已经都初始化为0)
dp[1] = dp[1 - volume[0]] + value[0] = 15
所以从后往前循环,每次取得状态不会和之前取得状态重合,这样每种物品就只取一次了。
import java.util.Scanner;public class Main {public static void main(String[] args) {Scanner scan = new Scanner(System.in);int N = scan.nextInt();int V = scan.nextInt();int[] volume = new int[N];int[] value = new int[N];for (int i = 0; i < N; i++) {volume[i] = scan.nextInt();value[i] = scan.nextInt();}int[] dp = new int[V + 1];for (int i = 0; i < N; i++) {//注意越界问题,且 j 需要从大到小遍历for (int j = V; j >= volume[i]; j--) {dp[j] = Math.max(dp[j], dp[j - volume[i]] + value[i]);}}System.out.println(dp[V]);}
}相关文章:

蓝桥杯 - 小明的背包1(01背包)
解题思路: 本题属于01背包问题,使用动态规划 dp[ j ]表示容量为 j 的背包的最大价值 注意: 需要时刻提醒自己dp[ j ]代表的含义,不然容易晕头转向 注意越界问题,且 j 需要倒序遍历 如果正序遍历 dp[1] dp[1 - vo…...

学习java第二十六天
Spring是一个开源框架,Spring是一个轻量级的Java 开发框架。它是为了解决企业应用开发的复杂性而创建的。框架的主要优势之一就是其分层架构,分层架构允许使用者选择使用哪一个组件,同时为 J2EE 应用程序开发提供集成的框架。Spring使用基本的…...
Go第三方框架--gin框架(二)
4. gin框架源码–Engine引擎和压缩前缀树的建立 讲了这么多 到标题4才开始介绍源码,主要原因还是想先在头脑中构建起 一个大体的框架 然后再填肉 这样不容易得脑血栓。标题四主要涉及标题2.3的步骤一 也就是 标题2.3中的 粗线框中的内容 4.1 Engine 引擎的建立 见…...
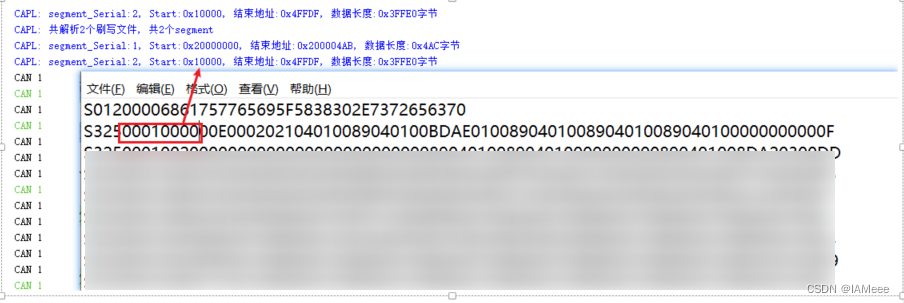
五分钟搞懂UDS刷写34/36/37服务(内含S19文件解读)
目录 34服务 36服务 37服务 S19文件介绍 理论太多总是让人头昏,通过举例的方法学习刷写是最好的办法,刷写中最重要的就是34/36/37服务之间的联动,在我当前的项目中37服务较为简单,等待36服务全部传输完成之后,发送…...

知识图谱智能问答系统技术实现
知识图谱是以一种结构化的方式存储和描述知识的数据集合,它将知识表示为节点和边的形式,并可以对这些节点和边进行有意义的存储、查询、连接和关系挖掘等操作。知识图谱不仅可以为人提供理解信息的能力,而且还能为机器提供对信息进行分析、推…...
【unity】如何汉化unity编译器
在【unity】如何汉化unity Hub这篇文章中,我们已经完成了unity Hub的汉化,现在让我们对unity Hub安装的编译器也进行下汉化处理。 第一步:在unity Hub软件左侧栏目中点击安装,选择需要汉化的编译器,再点击设置图片按钮…...

为什么Python不适合写游戏?
知乎上有热门个问题:Python 能写游戏吗?有没有什么开源项目? Python可以开发游戏,但不是好的选择 Python作为脚本语言,一般很少用来开发游戏,但也有不少大型游戏有Python的身影,比如࿱…...
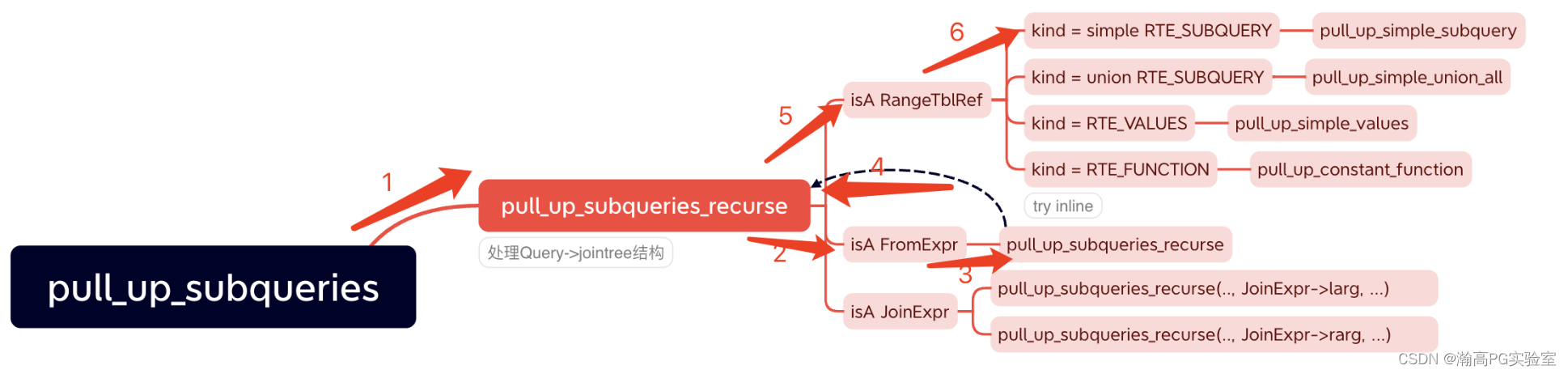
查询优化-提升子查询-UNION类型
瀚高数据库 目录 文档用途 详细信息 文档用途 剖析UNION类型子查询提升的条件和过程 详细信息 注:图片较大,可在浏览器新标签页打开。 SQL: SELECT * FROM score sc, LATERAL(SELECT * FROM student WHERE sno 1 UNION ALL SELECT * FROM student…...
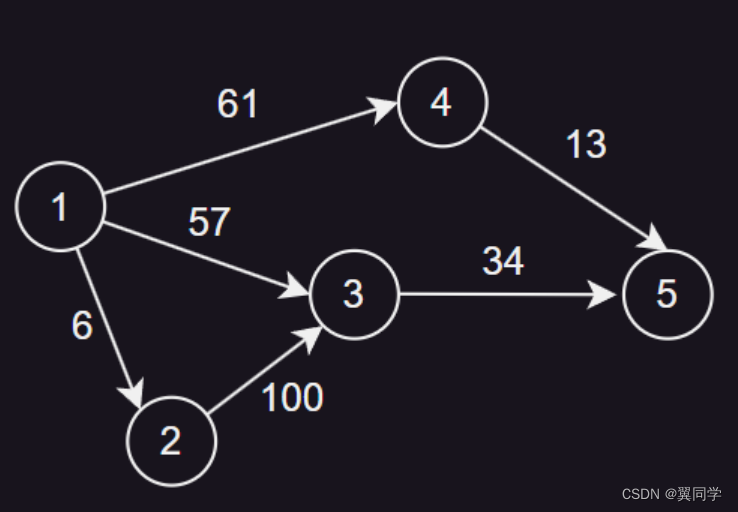
【数据结构 | 图论】如何用链式前向星存图(保姆级教程,详细图解+完整代码)
一、概述 链式前向星是一种用于存储图的数据结构,特别适合于存储稀疏图,它可以有效地存储图的边和节点信息,以及边的权重。 它的主要思想是将每个节点的所有出边存储在一起,通过数组的方式连接(类似静态数组实现链表…...
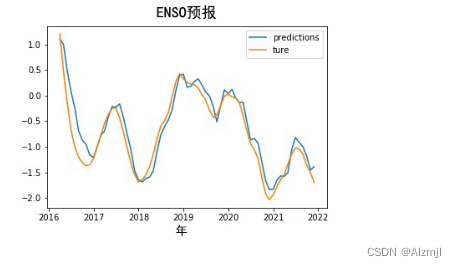
气象预测新篇章:Python人工智能的变革力量
Python是功能强大、免费、开源,实现面向对象的编程语言,在数据处理、科学计算、数学建模、数据挖掘和数据可视化方面具备优异的性能,这些优势使得Python在气象、海洋、地理、气候、水文和生态等地学领域的科研和工程项目中得到广泛应用。可以…...
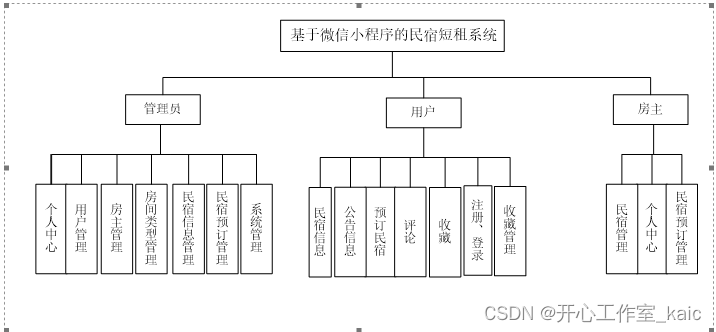
基于微信小程序的民宿短租系统设计与实现(论文+源码)_kaic
摘 要 随着社会的发展,出差、旅游成为常态,也就造成民宿短租市场的兴起。人们新到陌生的环境里找民宿一般都是通过中介。中介虽然可以快速找到合适的民宿但会收取大量的中介费用,这对刚到新环境里的人们来说是一笔大的资金支出。也有一些人通…...
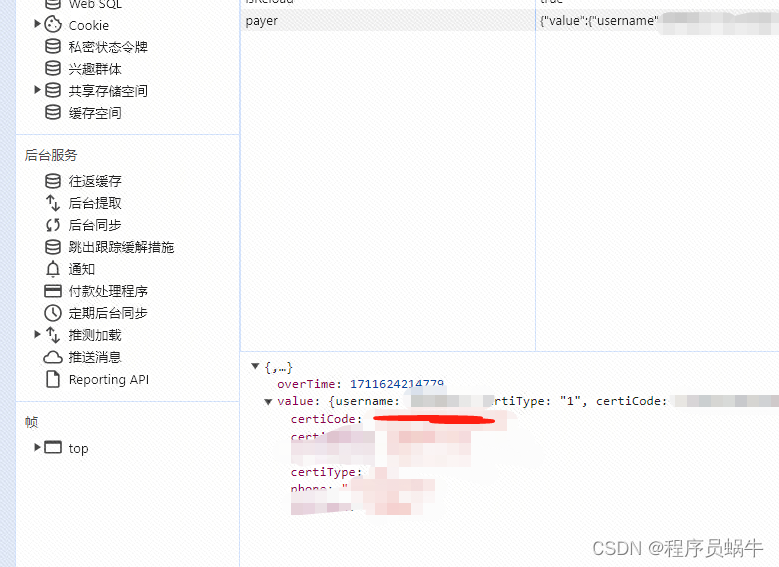
vue3开发前端表单缓存自定义指令,移动端h5必备插件
开发背景 公司需要开发一款移动端应用,使用vue开发,用户录入表单需要本地缓存,刷新页面,或者不小心关掉重新进来,上次录入的信息还要存在。 这里有两种方案,第一种就是像博客平台一样,实时保存…...
骗子查询系统源码
源码简介 小权云黑管理系统 V1.0 功能如下: 1.添加骗子,查询骗子 2.可添加团队后台方便审核用 3.在线反馈留言系统 4.前台提交骗子,后台需要审核才能过 5.后台使用光年UI界面 6.新增导航列表,可给网站添加导航友链 7.可添加云黑类…...

目标检测+车道线识别+追踪
一种方法: 车道线检测-canny边缘检测-霍夫变换 一、什么是霍夫变换 霍夫变换(Hough Transform)是一种在图像处理和计算机视觉中广泛使用的特征检测技术,主要用于识别图像中的几何形状,尤其是直线、圆和椭圆等常见形状…...
非wpf应用程序项目【类库、用户控件库】中使用HandyControl
文章速览 前言参考文章实现方法1、添加HandyControl包;2、添加资源字典3、修改资源字典内容 坚持记录实属不易,希望友善多金的码友能够随手点一个赞。 共同创建氛围更加良好的开发者社区! 谢谢~ 前言 wpf应用程序中,在入口项目中…...
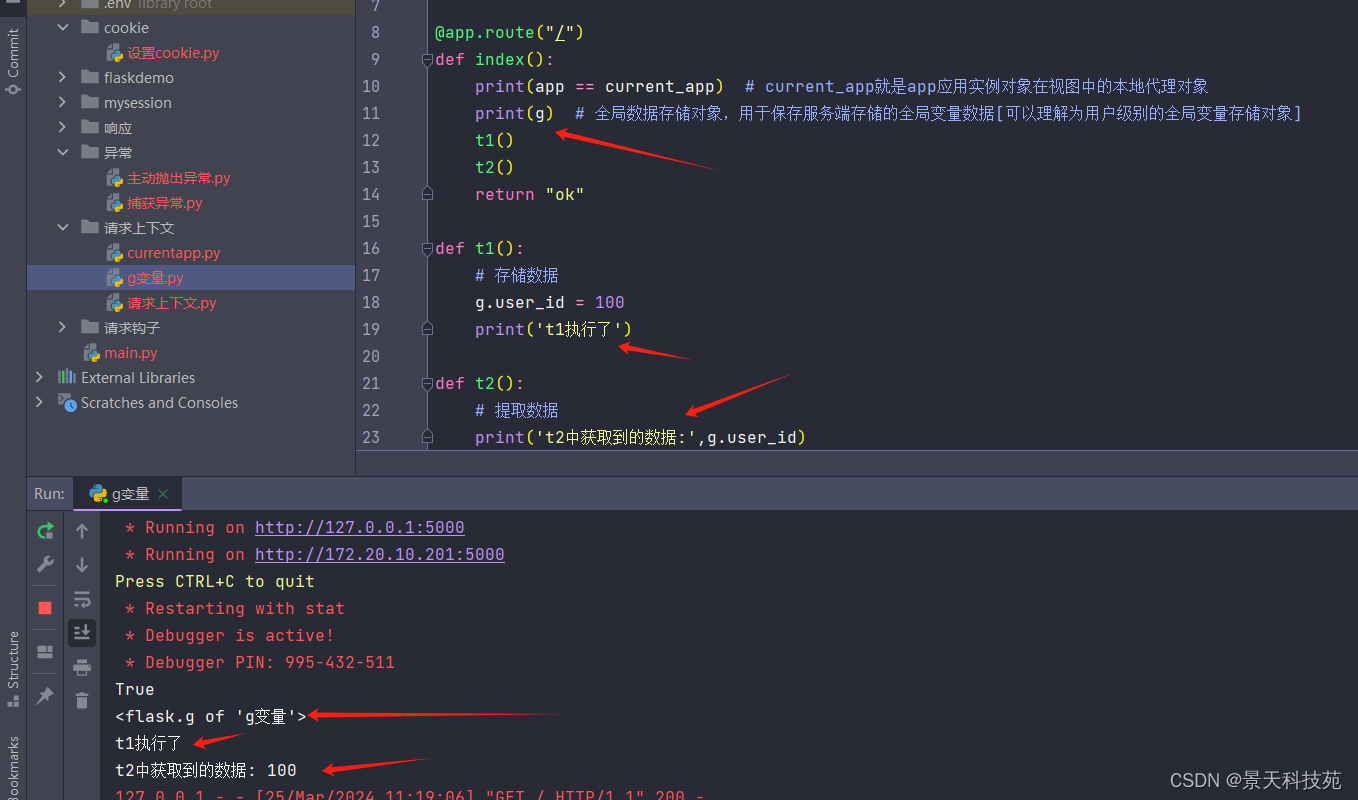
【python】flask执行上下文context,请求上下文和应用上下文原理解析
✨✨ 欢迎大家来到景天科技苑✨✨ 🎈🎈 养成好习惯,先赞后看哦~🎈🎈 🏆 作者简介:景天科技苑 🏆《头衔》:大厂架构师,华为云开发者社区专家博主,…...
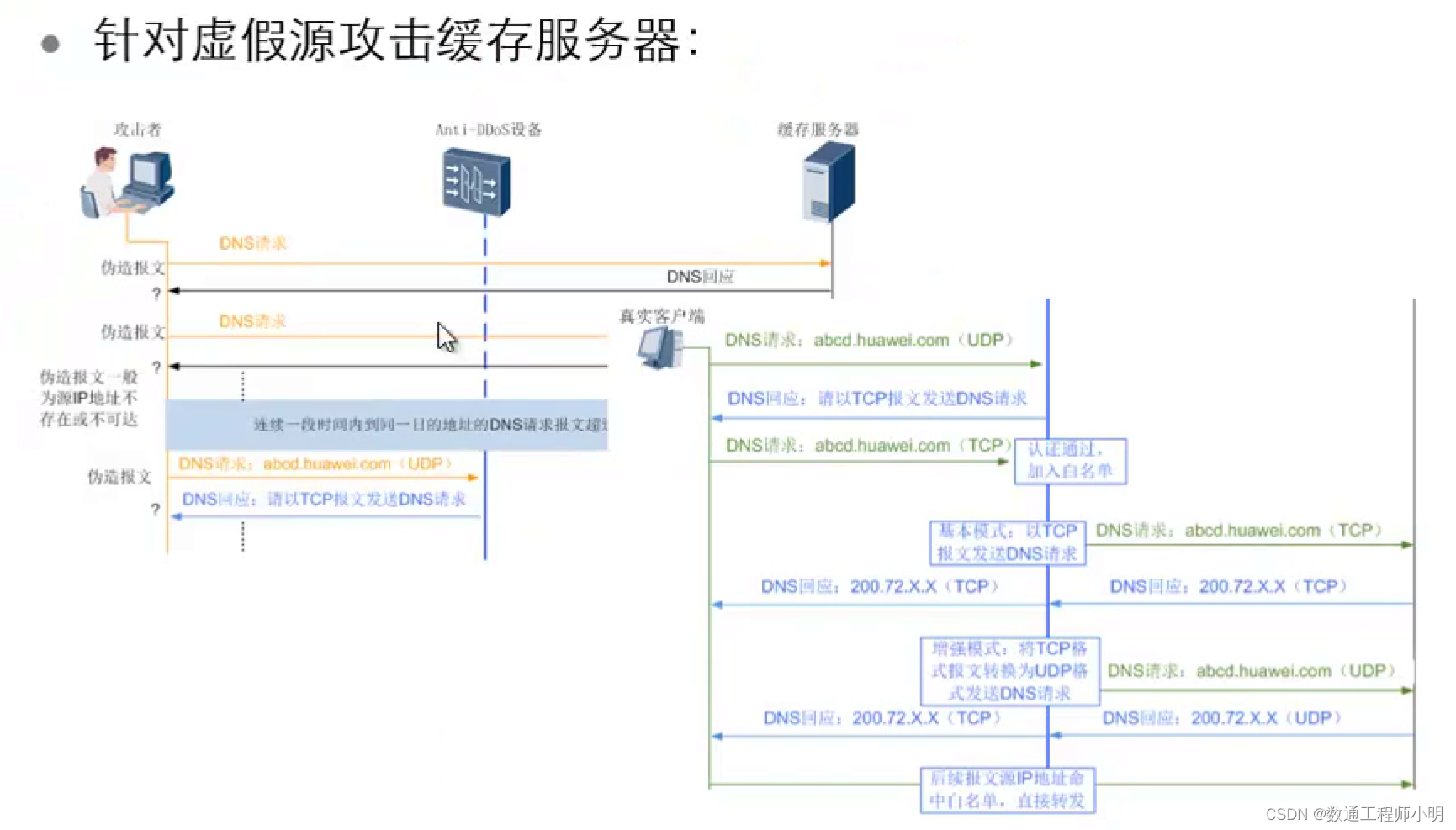
DDos系列攻击原理与防御原理
七层防御体系 静态过滤 命中黑名单 对确定是攻击的流量直接加入黑名单(源地址命中黑名单直接丢弃,缺乏机动性和扩展性) 畸形报文过滤 畸形报文攻击 TCP包含多个标记位,排列组合有规律 • 现象:TCP标记位全为1 …...
Python拆分PDF、Python合并PDF
WPS能拆分合并,但却是要输入编辑密码,我没有。故写了个脚本来做拆分,顺便附上合并的代码。 代码如下(extract.py) #!/usr/bin/env python """PDF拆分脚本(需要Python3.10)Usage::$ python extract.py <pdf-fil…...
经典总结大全-技巧总结-数据开发-基本函数-常识整理-经典面试题)
SqlServer(4)经典总结大全-技巧总结-数据开发-基本函数-常识整理-经典面试题
六、技巧 1、11,12的使用,在SQL语句组合时用的较多 “where 11” 是表示选择全部 “where 12”全部不选, 如: if strWhere !‘’ begin set strSQL ‘select count(*) as Total from [’ tblName ] where ’ strWhere …...
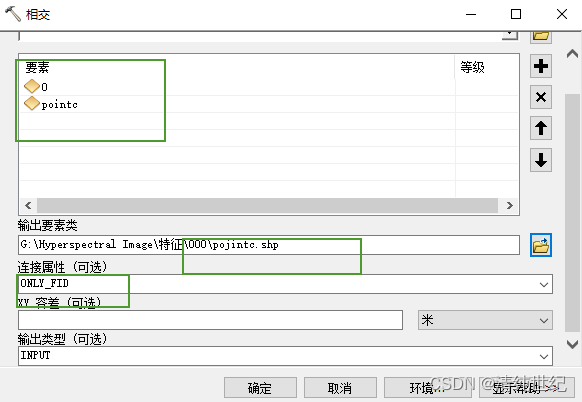
ArcGIS矢量裁剪矢量
一、利用相交工具 Arctoolbox工具一分析工具一叠加分析一相交...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...
