Chrome 插件各模块使用 Fetch 进行接口请求
Chrome 插件各模块使用 Fetch 进行接口请求
常规网页可以使用 fetch() 或 XMLHttpRequest API 从远程服务器发送和接收数据,但受到同源政策的限制。
内容脚本会代表已注入内容脚本的网页源发起请求,因此内容脚本也受同源政策的约束,插件的来源不受限制。
在插件 Service Worker 或前台标签页中执行的脚本可以与其源之外的远程服务器通信,前提是该插件请求跨源权限。
一、XMLHttpRequest 和 Fetch
fetch() 是专为 Service Worker 创建的,遵循远离同步操作的更广泛的网络趋势。Service Worker 之外的扩展支持 XMLHttpRequest() API,调用它会触发扩展 Service Worker 的提取处理程序
Service Worker 模块不支持 XMLHttpRequest,因此在新的插件中进行接口网络请求需使用 Fetch
const response = await fetch('https://www.example.com/greeting.json'')
console.log(response.statusText);
二、Fetch 请求
1. 请求插件内容模块
每个正在运行的插件都存在于各自独立的安全源中。该插件无需请求额外的权限,即可调用 fetch() 来获取安装范围内的资源
如果某个插件在 config_resources/ 文件夹中包含一个名为 config.json 的 JSON 配置文件,则该插件可以检索该文件的内容
const response = await fetch('/config_resources/config.json');
const jsonData = await response.json();
2. 跨源请求
需在 manifest.json 中添加 host_permissions 字段
{"name": "My extension","host_permissions": ["https://www.douban.com/"],
}
3. content_scripts 中进行网络请求
manifest.json文件配置
{"content_scripts": [{"matches": ["https://movie.douban.com/*"],"css": ["content/index.css"],"js": ["content/jquery.js", "content/index.js"]}],"host_permissions": ["https://movie.douban.com/*"],
}
content/index.js进行数据请求
const response = await fetch("https://movie.douban.com/j/tv/recommend_groups")
if (!response.ok) {throw new Error('Network response was not ok')
}
const allData = await response.json()
console.log('content index allData', allData)
- 日志输出
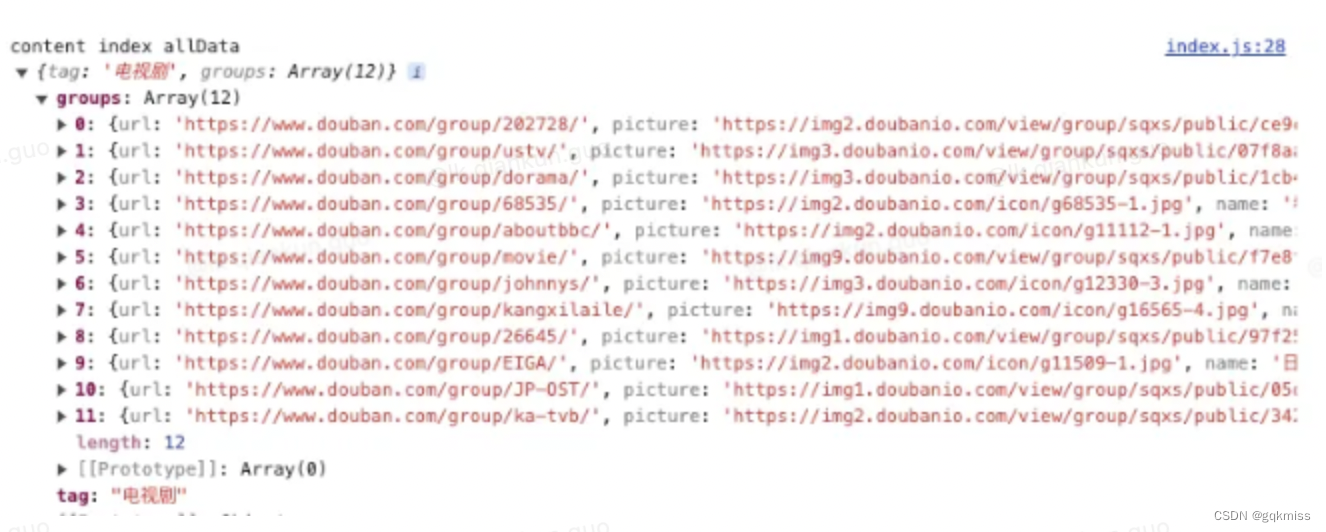
4. service_worker 中进行网络请求
manifest.json文件配置
{"host_permissions": ["https://movie.douban.com/*"],
}
service_worker.js进行数据请求
const response = await fetch("https://movie.douban.com/j/tv/recommend_groups")
if (!response.ok) {throw new Error('Network response was not ok')
}
const allData = await response.json()
console.log('service worker allData', allData)
- 日志输出
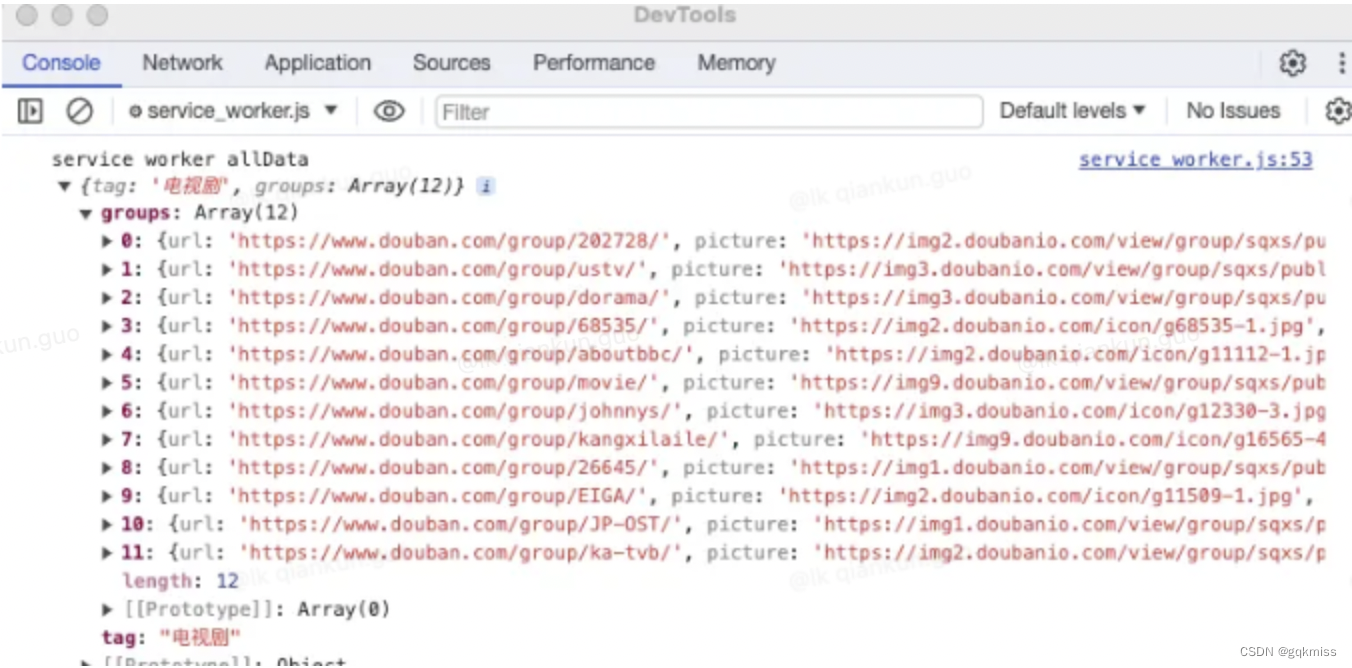
5. Action 中进行网络请求
manifest.json文件配置
{"host_permissions": ["https://movie.douban.com/*"],
}
index.js进行数据请求
const response = await fetch("https://movie.douban.com/j/tv/recommend_groups")
if (!response.ok) {throw new Error('Network response was not ok')
}
const allData = await response.json()
console.log('Action allData', allData)
- 日志输出
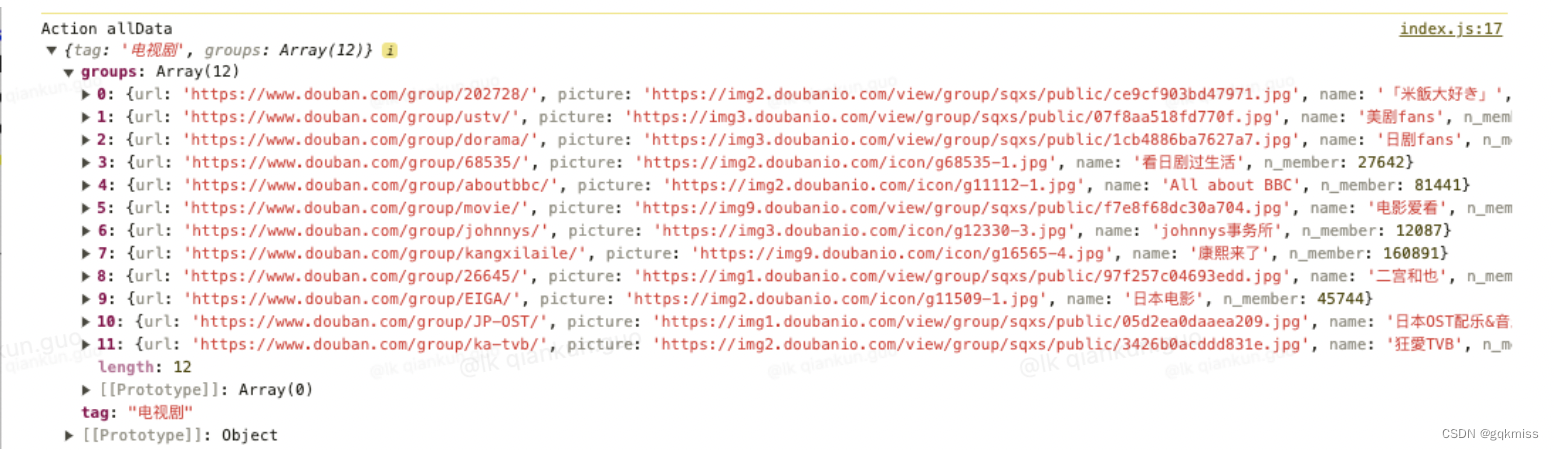
总结
Chrome插件中的网络请求和普通web是一样的,只不过从常用的AJAX换成了Fetch- 进行跨域请求的时候一定要配置
manifest.json文件 - 一般请求都需要和
cookies进行配合,关于cookies API可以查看 【Chrome 浏览器插件 cookies API 解析
】
相关文章:

Chrome 插件各模块使用 Fetch 进行接口请求
Chrome 插件各模块使用 Fetch 进行接口请求 常规网页可以使用 fetch() 或 XMLHttpRequest API 从远程服务器发送和接收数据,但受到同源政策的限制。 内容脚本会代表已注入内容脚本的网页源发起请求,因此内容脚本也受同源政策的约束,插件的来…...

内存可见性
内存可见性 一:内存可见性1.2: 二:解决内存可见性问题2.1 volatile关键字2.2:synchronized关键字解决内存可见性问题 一:内存可见性 public class Demo1 {public static int count 0;public static void main(String[] args) throws InterruptedException {Thread t1new Thre…...
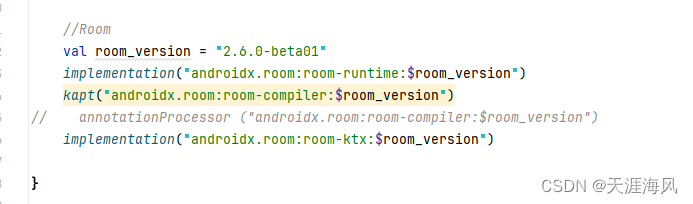
Android room 在dao中不能使用挂起suspend 否则会报错
错误: Type of the parameter must be a class annotated with Entity or a collection/array of it. kotlin.coroutines.Continuation<? super kotlin.Unit> $completion); 首先大家检查一下几个点 一、kotlin-kapt 二、 是否引入了 room-ktx 我是2024年…...
【stable diffusion扩散模型】一篇文章讲透
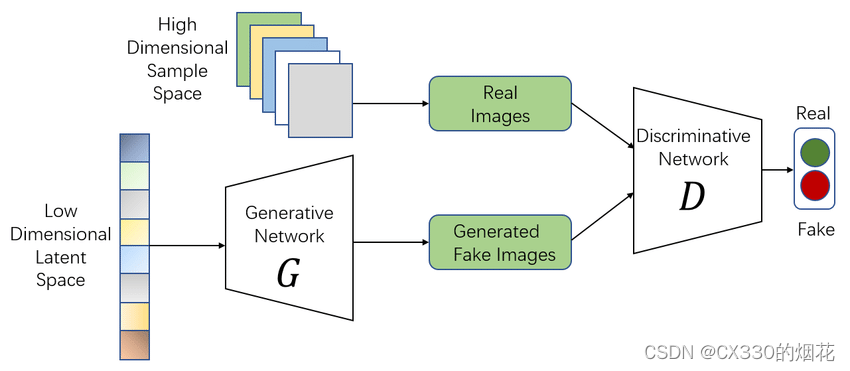
目录 一、引言 二、Stable Diffusion的基本原理 1 扩散模型 2 Stable Diffusion模型架构 3 训练过程与算法细节 三、Stable Diffusion的应用领域 1 图像生成与艺术创作 2 图像补全与修复 3 其他领域 四、Stable Diffusion的优势与挑战 👉优势 …...

数据链路层之信道:数字通信的桥梁与守护者
✨✨ 欢迎大家来访Srlua的博文(づ ̄3 ̄)づ╭❤~✨✨ 🌟🌟 欢迎各位亲爱的读者,感谢你们抽出宝贵的时间来阅读我的文章。 我是Srlua小谢,在这里我会分享我的知识和经验。&am…...

SQL109 纠错4(组合查询,order by..)
SELECT cust_name, cust_contact, cust_email FROM Customers WHERE cust_state MI UNION SELECT cust_name, cust_contact, cust_email FROM Customers WHERE cust_state IL ORDER BY cust_name;order by子句,必须位于最后一条select语句之后...

Spring Boot + Vue 实现文件导入导出功能
文章目录 1、概述2、后端实现(Spring Boot)3、前端实现(Vue)4、总结 1、概述 在现代Web应用开发中,文件的导入导出是一个常见的需求。Spring Boot作为后端开发的强大框架,搭配前端框架Vue,可…...
vue watch 深度监听
vue2文档:API — Vue.js vue3文档:侦听器 | Vue.js watch 可以用来监听页面中的数据,但如果监听的源是对象或数组,则使用深度监听,强制深度遍历源,以便在深度变更时触发回调。 一,监听 <t…...
Qt源码调试步骤记录
1.源码: 两种方式,要么安装qt时选择source,要么从官网下载源码,然后在qt creator中设置路径。二选一即可。我选的第二种。 1.1.第一种,安装时选择source: 1.2.第二种,下载源码设置路径&#x…...
)
大数据面试英文自我介绍参考(万字长文)
发现有一个怪圈,如果码农年龄35+,除非非常匹配,不然在国内企业筛选可能就筛选不过。国外码农可以干到40+、50+。一些外企,对年龄35+的码农依然青睐。这些外企对英文是有要求,通常是要英文自我介绍,下面提供一些英文自我介绍参考。 参考1: Good morning/afternoon, I a…...

外包干了5天,技术退步明显.......
先说一下自己的情况,大专生,18年通过校招进入杭州某软件公司,干了接近4年的功能测试,今年年初,感觉自己不能够在这样下去了,长时间呆在一个舒适的环境会让一个人堕落! 而我已经在一个企业干了四年的功能测…...
Docket常见的软件部署1
1 安装MySQL # 查看MySQL镜像 docker search mysql # 拉起镜像 docker pull mysql:5.7 # 创建MySQL数据映射卷,防止数据不丢失 mkdir -p /hmoe/tem/docker/mysql/data/ # 启动镜像 docker run -d --name mysql -e MYSQL_ROOT_PASSWORD123456 -p 3306:3306 -v /home…...
Qt源程序编译及错误问题解决
Error 5 while parsing C:/qt-everywhere-src-6.6.2/qt-build/qtdeclarative/src/qmlmodels/meta_types/qt6qmlmodels_release_metatypes.json: illegal value .json 文件为空文件0字节,加 “[]”,不要引号。可以解决这类错误。 Qt编译 Qt for Windows…...
)
作业练习(python)
第一题: cel eval(input()) fah 9 / 5 * cel 32 print("%.1f" % fah) 第二题: radius, length eval(input()) area radius * radius * 3.14159267 volume area * length print("%.2f" % area) print("%.2f" …...
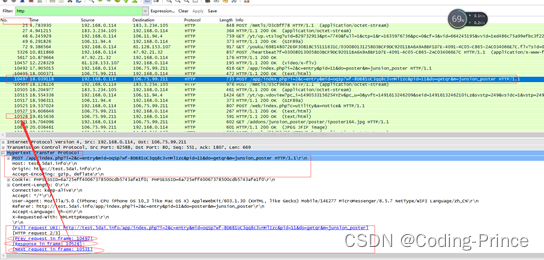
Wireshark使用相关
1.wireshark如何查看RST包 tcp.flags.reset1 RST表示复位,用来异常的关闭连接,在TCP的设计中它是不可或缺的。发送RST包关闭连接时,不必等缓冲区的包都发出去(不像上面的FIN包),直接就丢弃缓存区的包发送R…...

相机标定学习记录
相机标定是计算机视觉和机器视觉领域中的一项基本技术,它的主要目的是通过获取相机的内部参数(内参)和外部参数(外参),以及镜头畸变参数,建立起现实世界中的点与相机成像平面上对应像素点之间准…...

CSS 滚动条样式修改
1、滚动条整体部分 使用 ::-webkit-scrollbar 注意:这个必须要加,不然修改的样式不生效 ::-webkit-scrollbar {width: 10px;//修改滚动条宽度 }2、滚动条中的滑块 使用 ::-webkit-scrollbar-thumb ::-webkit-scrollbar-thumb {border-radius: 8px;b…...
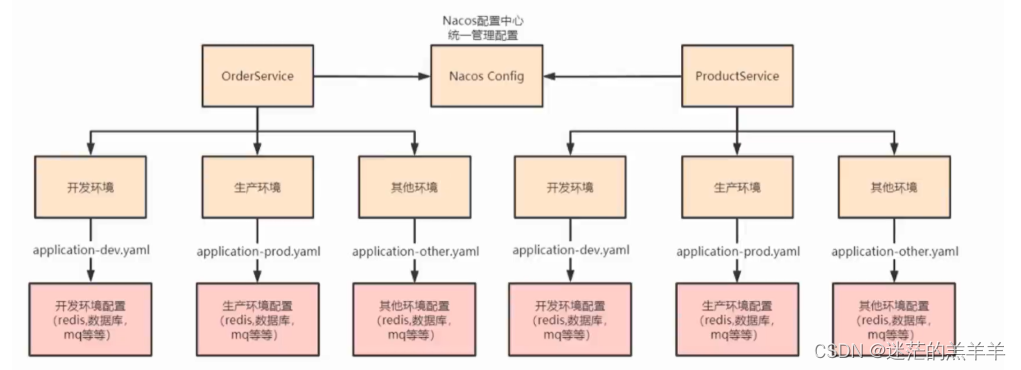
谈谈配置中心?
配置中心可以做集中式的服务配置管理,比如配置一些数据库连接的URL,一些共用的配置且可动态调整的参数。如果不采用集中式的管理,会导致修改起来特别麻烦,一个个的修改特别繁琐。 Nacos Config配置中心中采用的是客户端拉取数据&a…...
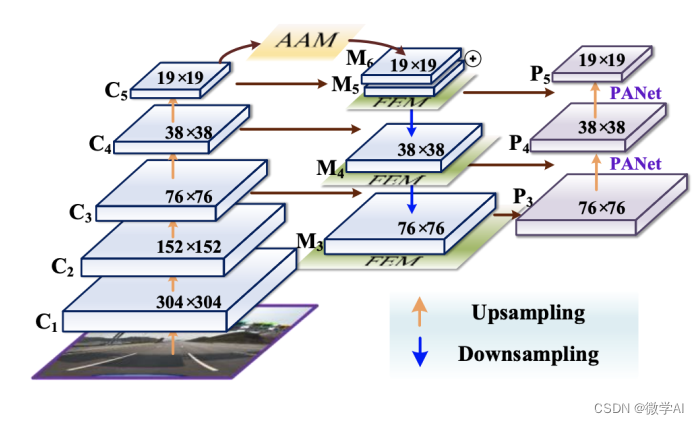
人工智能(pytorch)搭建模型25-基于pytorch搭建FPN特征金字塔网络的应用场景,模型结构介绍
大家好,我是微学AI,今天给大家介绍一下人工智能(pytorch)搭建模型25-基于pytorch搭建FPN特征金字塔网络的应用场景,模型结构介绍。特征金字塔网络(FPN)是一种深度学习模型结构,主要应用于目标检测任务中&am…...
JRT业务开发起步
这是一段充满挑战与奋斗的旅程,自第一行Java代码的写下起,便历经重重险阻。从细微的代码行,逐步汇聚成实用的工具类方法;从工具类方法的积累,逐渐构建起功能强大的工具包;再从工具包的整合,最终…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...

Windows电脑能装鸿蒙吗_Windows电脑体验鸿蒙电脑操作系统教程
鸿蒙电脑版操作系统来了,很多小伙伴想体验鸿蒙电脑版操作系统,可惜,鸿蒙系统并不支持你正在使用的传统的电脑来安装。不过可以通过可以使用华为官方提供的虚拟机,来体验大家心心念念的鸿蒙系统啦!注意:虚拟…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...
