数据结构——二叉树——堆
前言:
在前面我们已经学习了数据结构的基础操作:顺序表和链表及其相关内容,今天我们来学一点有些难度的知识——数据结构中的二叉树,今天我们先来学习二叉树中堆的知识,这部分内容还是非常有意思的,下面我们就开始慢慢学习
准备工作:本人习惯将文件放在test.c、SeqList.c、SeqList.h三个文件中来实现,其中test.c用来放主函数,SeqList.c用来放调用的函数,SeqList.h用来放头文件和函数声明
一、什么是树
在正式进行二叉树的学习之前,我们要了解一下树是何物,其实我们经常讲到的计算机中的树其实是以数组的形式存在在内存中的,只是它的可以形象化成树的形状,如下:
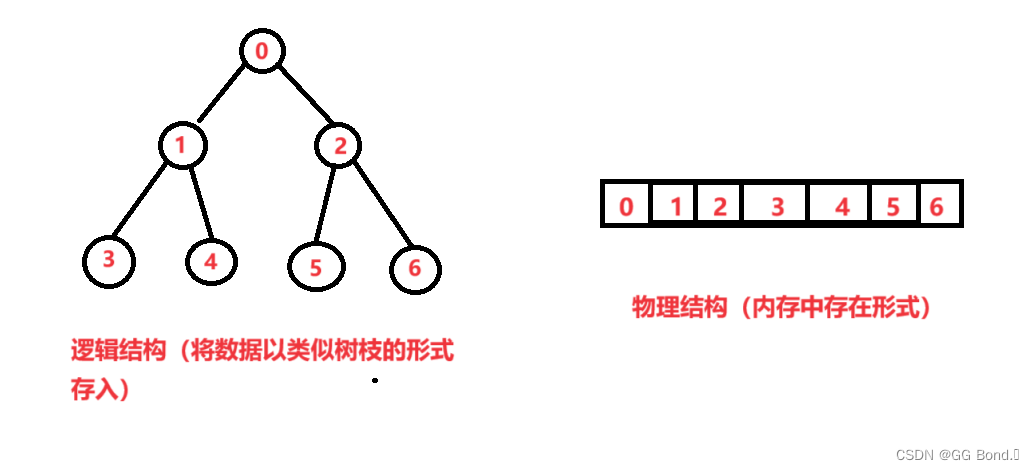
如图,其中0所在位置被称为树顶或者树根都可以,下面的称为子树,其中1所在分叉称为左子树,2所在分叉成为右子树
还有一些规则如下:

对于学过离散数学的同学来说这部分知识并不难,没有学过的自己再去搜一下了解一下吧,这里只讲了一些大概内容
二、什么是堆
树里面有几个特殊的概念,例如完全二叉树和满二叉树,而堆就是完全二叉树的一种,完全二叉树就是除了最后一层外,其他层节点数达到最大
堆与普通的完全二叉树的不同在于它的大小堆的性质
大堆:树任何一个父亲>=孩子
小堆:树任何一个父亲<=孩子
例如:
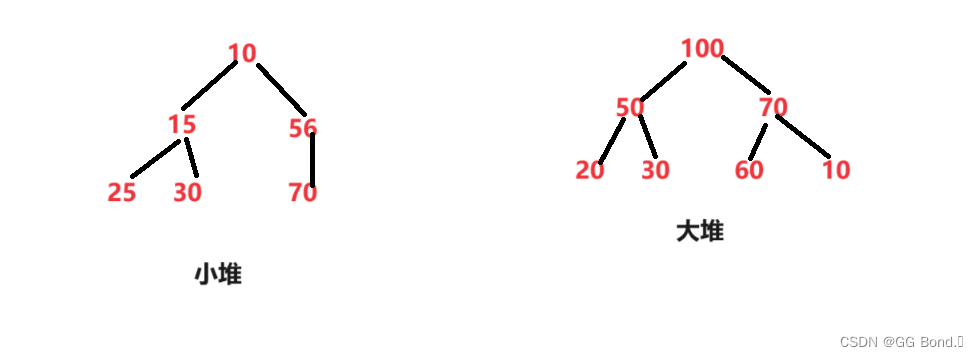
三、堆的节点结构
堆用的顺序表的结构,所以堆的节点结构与顺序表差异不大
typedef int HPDataType;
typedef struct Heap
{HPDataType* a;int sz;int capacity;
}HP;
堆的节点结构很简单,定义一个指针,两个表示容量的整形即可
四、堆的基本操作
//初始化
void HeapInit(HP* php);
//销毁
void HeapDestory(HP* php);
//插入
void HeapPush(HP* php, HPDataType x);
//删除
void HeapPop(HP* php);
//找堆顶元素
HPDataType HeapTop(HP* php);
//判断是否为空
bool HeapEmpty(HP* php);
//算个数
int HeapSize(HP* php);看上面的函数声明部分我们就可以看到我们每一步要实现的内容,接下来,我们就来一步一步进行实现
1、初始化
//初始化
void HeapInit(HP* php)
{assert(php);php->a = NULL;php->capacity = 0;php->sz = 0;
}
2、销毁
//销毁
void HeapDestory(HP* php)
{free(php->a);free(php);
}
3、插入元素
插入元素时要先检查空间是否够用,如果不够用要先进行扩容
//交换
void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}
//删除//向上调整(小堆)
void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}
//向下调整
void AdjustDown(int* a, int n, int parent)
{int child = parent * 2 + 1;while (child<n){if (child+1<n&&a[child + 1] < a[child]){++child;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}//插入
void HeapPush(HP* php, HPDataType x)
{assert(php);if (php->sz == php->capacity){int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newcapacity);php->a = tmp;php->capacity = newcapacity;}php->a[php->sz] = x;php->sz++;//向上调整AdjustUp(php->a, php->sz - 1);
}
在这一步我们还创建了几个其他的函数分担一些功能,这些函数在后文中也有应用
4、判断栈顶元素是否为空
这一步在下面有用到,例如当删除树根元素时,如果树根元素为空就无法操作,所以需要判断树根元素是否为空
//判断是否为空
bool HeapEmpty(HP* php)
{assert(php);return php->sz == 0;
}
5、删除元素
这里删除元素是删除树根元素
//删除
void HeapPop(HP* php)
{assert(php);assert(!HeapEmpty(php));Swap(&php->a[0], &php->a[php->sz - 1]);php->sz--;//向下调整AdjustDown(php->a, php->sz,0);
}
6、返回树根元素
//找堆顶元素
HPDataType HeapTop(HP* php)
{assert(php);assert(!HeapEmpty(php));return php->a[0];
}
7、算个数
//算个数
int HeapSize(HP* php)
{assert(php);return php->sz;
}五、完整代码实例
SeqList.h
typedef int HPDataType;
typedef struct Heap
{HPDataType* a;int sz;int capacity;
}HP;//初始化
void HeapInit(HP* php);
//销毁
void HeapDestory(HP* php);
//插入
void HeapPush(HP* php, HPDataType x);
//删除
void HeapPop(HP* php);
//找堆顶元素
HPDataType HeapTop(HP* php);
//判断是否为空
bool HeapEmpty(HP* php);
//算个数
int HeapSize(HP* php);test.c
//堆
int main()
{HP hp;HeapInit(&hp);int a[] = { 65,100,70,32,50,60 };for (int i = 0; i < sizeof(a) / sizeof(int); i++){HeapPush(&hp, a[i]);}while (!HeapEmpty(&hp)){int top = HeapTop(&hp);printf("%d ", top);HeapPop(&hp);}return 0;
}SeqList.c
//堆
//初始化
void HeapInit(HP* php)
{assert(php);php->a = NULL;php->capacity = 0;php->sz = 0;
}
//销毁
void HeapDestory(HP* php)
{free(php->a);free(php);
}
//交换
void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}
//删除//向上调整(小堆)
void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}
//向下调整
void AdjustDown(int* a, int n, int parent)
{int child = parent * 2 + 1;while (child<n){if (child+1<n&&a[child + 1] < a[child]){++child;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}//插入
void HeapPush(HP* php, HPDataType x)
{assert(php);if (php->sz == php->capacity){int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newcapacity);php->a = tmp;php->capacity = newcapacity;}php->a[php->sz] = x;php->sz++;//向上调整AdjustUp(php->a, php->sz - 1);
}
//删除
void HeapPop(HP* php)
{assert(php);assert(!HeapEmpty(php));Swap(&php->a[0], &php->a[php->sz - 1]);php->sz--;//向下调整AdjustDown(php->a, php->sz,0);
}
//判断是否为空
bool HeapEmpty(HP* php)
{assert(php);return php->sz == 0;
}
//找堆顶元素
HPDataType HeapTop(HP* php)
{assert(php);assert(!HeapEmpty(php));return php->a[0];
}
//算个数
int HeapSize(HP* php)
{assert(php);return php->sz;
}相关文章:

数据结构——二叉树——堆
前言: 在前面我们已经学习了数据结构的基础操作:顺序表和链表及其相关内容,今天我们来学一点有些难度的知识——数据结构中的二叉树,今天我们先来学习二叉树中堆的知识,这部分内容还是非常有意思的,下面我们…...
算法学习——LeetCode力扣图论篇3(127. 单词接龙、463. 岛屿的周长、684. 冗余连接、685. 冗余连接 II)
算法学习——LeetCode力扣图论篇3 127. 单词接龙 127. 单词接龙 - 力扣(LeetCode) 描述 字典 wordList 中从单词 beginWord 和 endWord 的 转换序列 是一个按下述规格形成的序列 beginWord -> s1 -> s2 -> … -> sk: 每一对相…...

状态模式详解:管理对象状态的利器
在软件设计中,我们经常会遇到需要根据对象的不同状态来执行不同行为的情况。为了优雅地管理这些状态及其对应的行为,状态模式(State Pattern)应运而生。本文将深入探讨状态模式的使用条件、Java代码实现,并结合现实社会…...

探索----------------阿里云
目录 一、阿里云四大件 1、云服务器ECS 2、云数据库RDS 3、负载均衡SLB 4、对象存储OSS 5、其他的云计算产品 1)内容分发网络CDN 2)专有网络 VPC 二、linux发行版本 三、你平时对系统会怎么优化(五大负载) 1、cpu 使用率…...
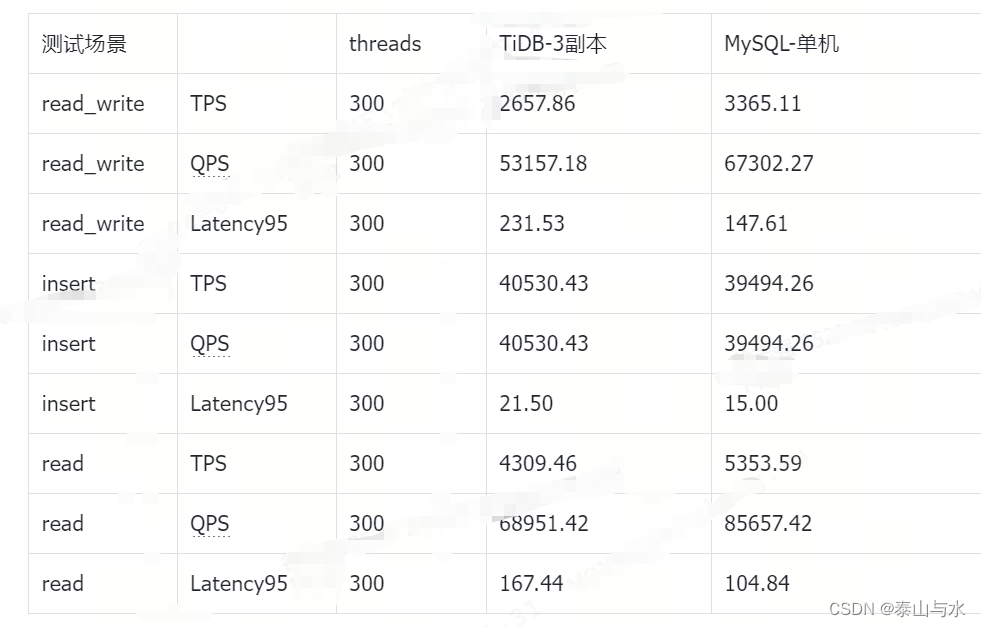
Tidb和MySQL性能简单测试对比
一、单SQL性能对比 由于TiDB的并发能力优秀,但是单个SQL执行延迟较差,为了客观对比,所以只用1个线程来压测tidb和mysql,以观察延迟情况 二、并发SQL性能对比 TiDB:v6.5.2 MySQL:8.0.26 (单机) 三、结论 …...

2024.2.6力扣每日一题——魔塔游戏
2024.2.6 题目来源我的题解方法一 贪心优先队列 题目来源 力扣每日一题;题序:LCP 30 我的题解 方法一 贪心优先队列 思路:使用贪心的思想,从左到右遍历,若遇到加上当前房间的生命值后小于等于0,由于需要…...

C# OAuth单点登录的实现
原理 单点登录(Single Sign-On,简称SSO)是一种身份验证技术,它允许用户使用一组凭据(如用户名和密码)登录多个相关但独立的系统,而无需在每个系统中都进行登录操作。下面是一个简单的SSO实现示…...

AtCoder Beginner Contest 347 (ABCDEF题)视频讲解
A - Divisible Problem Statement You are given positive integers N N N and K K K, and a sequence of length N N N, A ( A 1 , A 2 , … , A N ) A(A_1,A_2,\ldots,A_N) A(A1,A2,…,AN). Extract all elements of A A A that are multiples of K K K, divi…...
【vue2+antvx6】报错Cannot read properties of undefined (reading ‘toUpperCase‘)
我的代码是这样的 <el-collapseref"collapse"v-model"active"accordionclass"collapseStart"change"collapsechange"><el-collapse-item:name"String(index 1)"v-for"(i, index) in List":key"in…...

主流的开发语言、环境及其特点
主流的开发语言及其特点: 1. Python:以其简洁的语法和强大的库支持而闻名,适用于数据科学、人工智能和网络开发等领域。 2. Java:跨平台的编程语言,广泛应用于企业级应用、Android 开发和大型系统开发。 3. C…...

Android知识 - 代码混淆ProGuard规则介绍
ProGuard 的规则及示例 规则概述 ProGuard 是一个代码优化工具,它通过移除未使用的代码、重命名类、字段和方法等方式来减小应用的大小。在 ProGuard 的配置文件中,我们可以定义一系列的规则来控制优化和混淆的过程。 规则语法 ProGuard 的规则通常包…...

【Linux的进程篇章 - 冯诺依曼的体系结构】
Linux学习笔记---005 Linux冯诺依曼体系结构理解1、冯诺依曼体系结构1.1、冯诺依曼体系结构1.2、硬件层面1.3、数据层面1.4、那么冯诺依曼体系能干什么呢? 2、操作系统(Operastor System)2.1、概念2.2、操作系统层的核心功能 3、进程的初步理解 Linux冯诺依曼体系结…...
)
flask-(数据连接池的使用,定制命令,信号的使用,表关系的建立和查询)
文章目录 连接池实例flask定制命令flask 缓存的使用flask信号的使用sqlalchemy原生操作sqlalchemy操作表flask orm操作表一对多的增加和跨表查询 (一对一只需要关联字段加上 ,uniqueTrue)多对多关系的增加和查询多对多基本的增删改查 连接池 import pymy…...
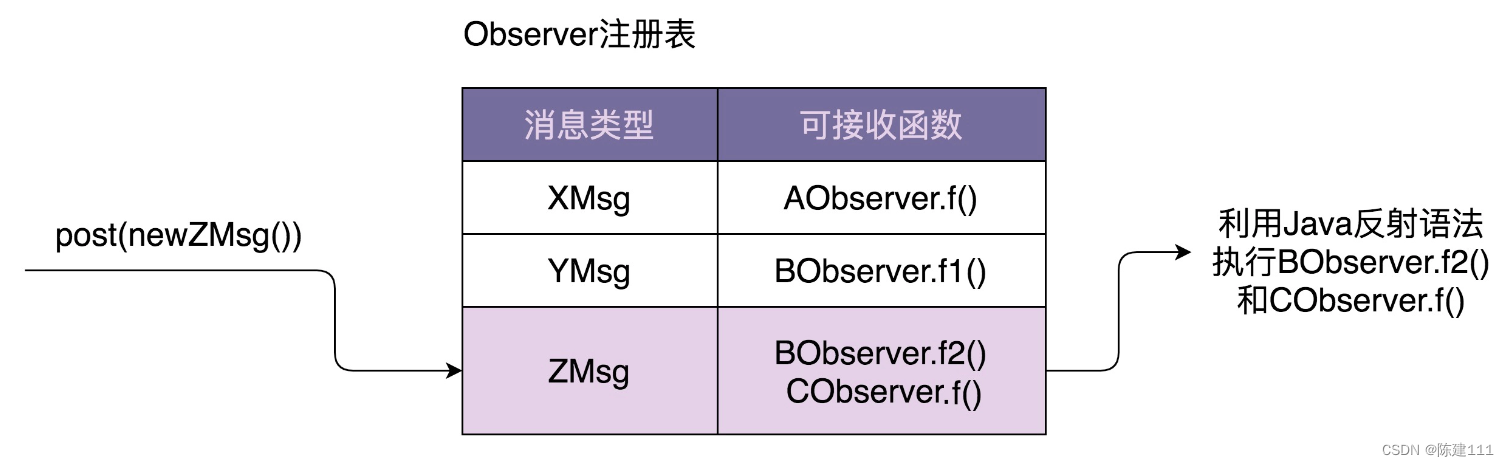
设计模式学习笔记 - 设计模式与范式 -行为型:2.观察者模式(下):实现一个异步非阻塞的EventBus框架
概述 《1.观察者模式(上)》我们学习了观察者模式的原理、实现、应用场景,重点节介绍了不同应用场景下,几种不同的实现方式,包括:同步阻塞、异步非阻塞、进程内、进程间的实现方式。 同步阻塞最经典的实现…...
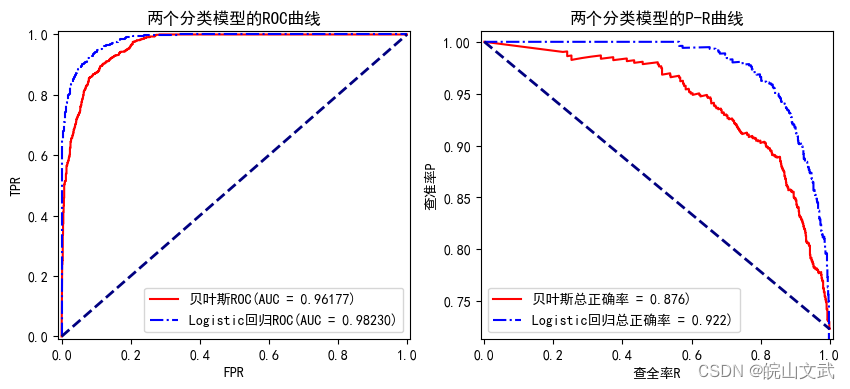
数据挖掘|贝叶斯分类器及其Python实现
分类分析|贝叶斯分类器及其Python实现 0. 分类分析概述1. Logistics回归模型2. 贝叶斯分类器2.1 贝叶斯定理2.2 朴素贝叶斯分类器2.2.1 高斯朴素贝叶斯分类器2.2.2 多项式朴素贝叶斯分类器 2.3 朴素贝叶斯分类的主要优点2.4 朴素贝叶斯分类的主要缺点 3. 贝叶斯分类器在生产中的…...
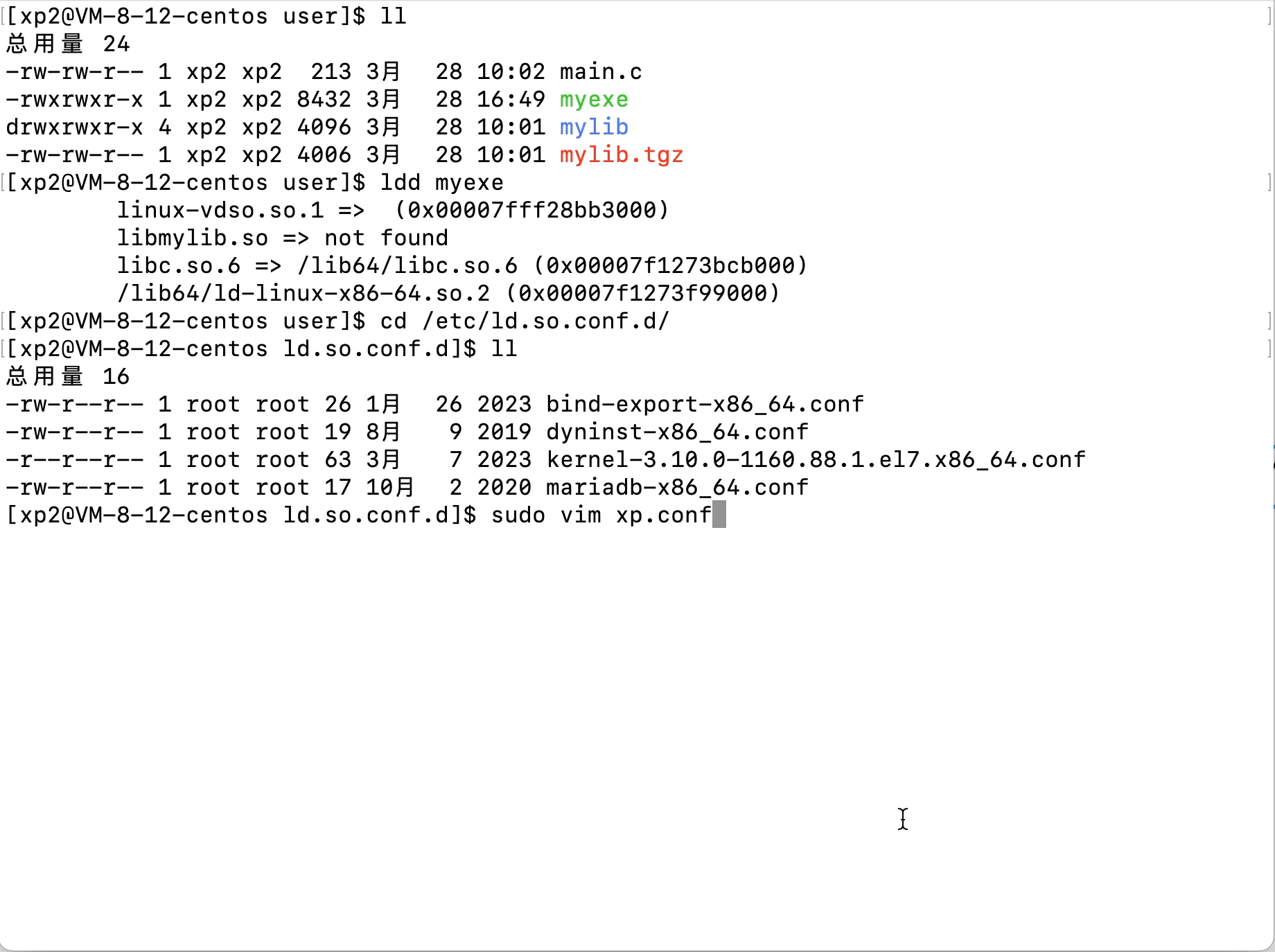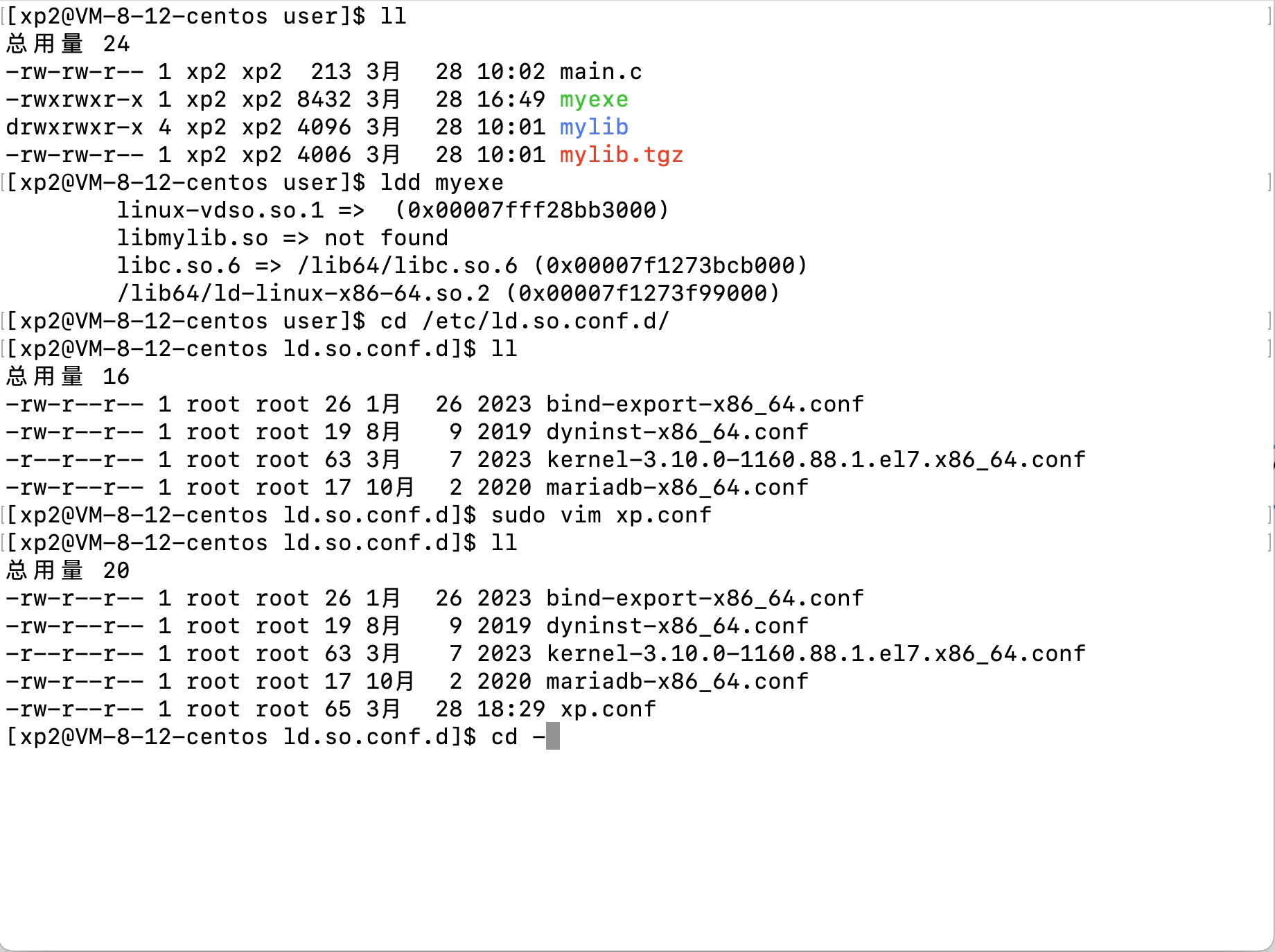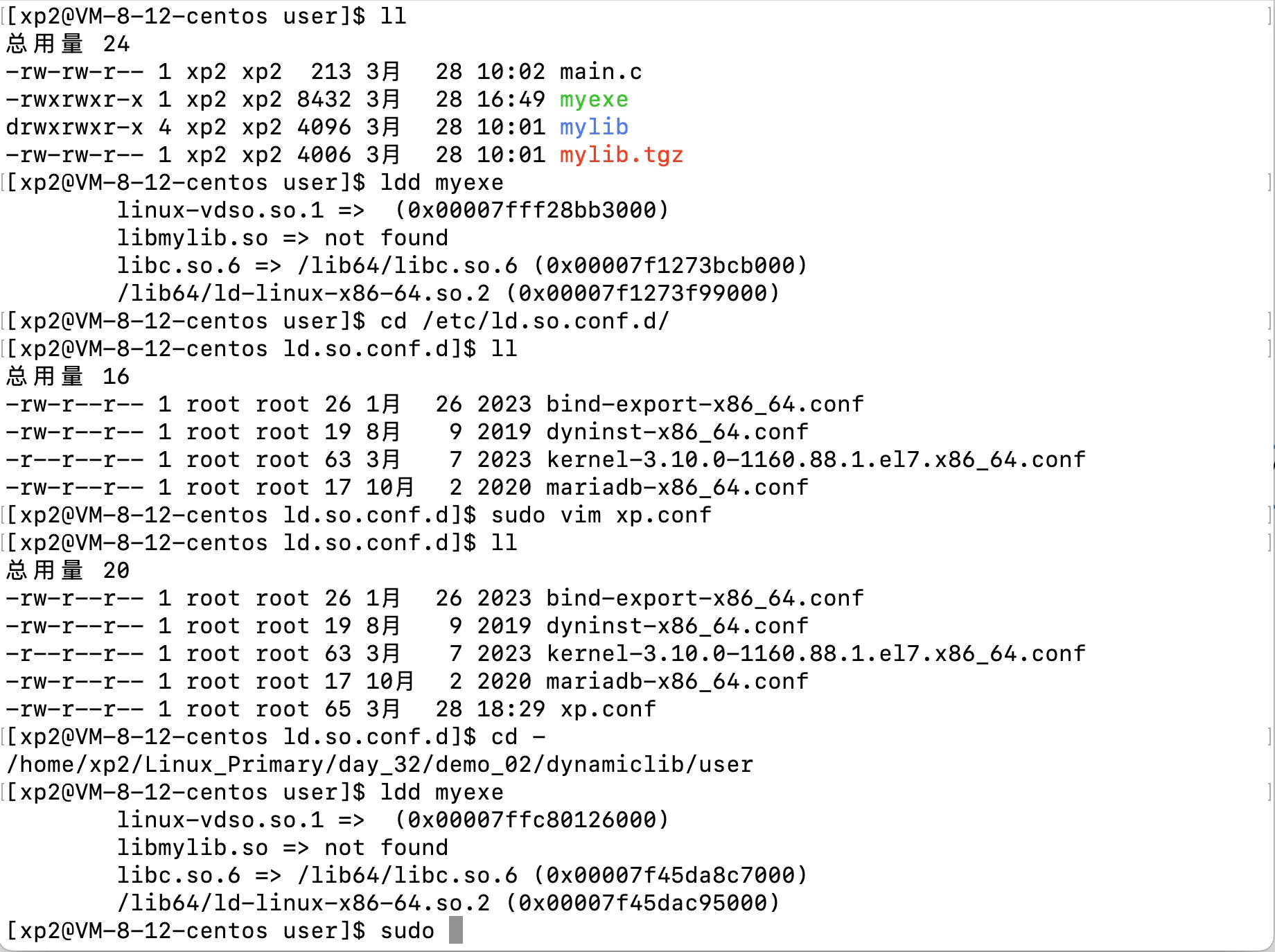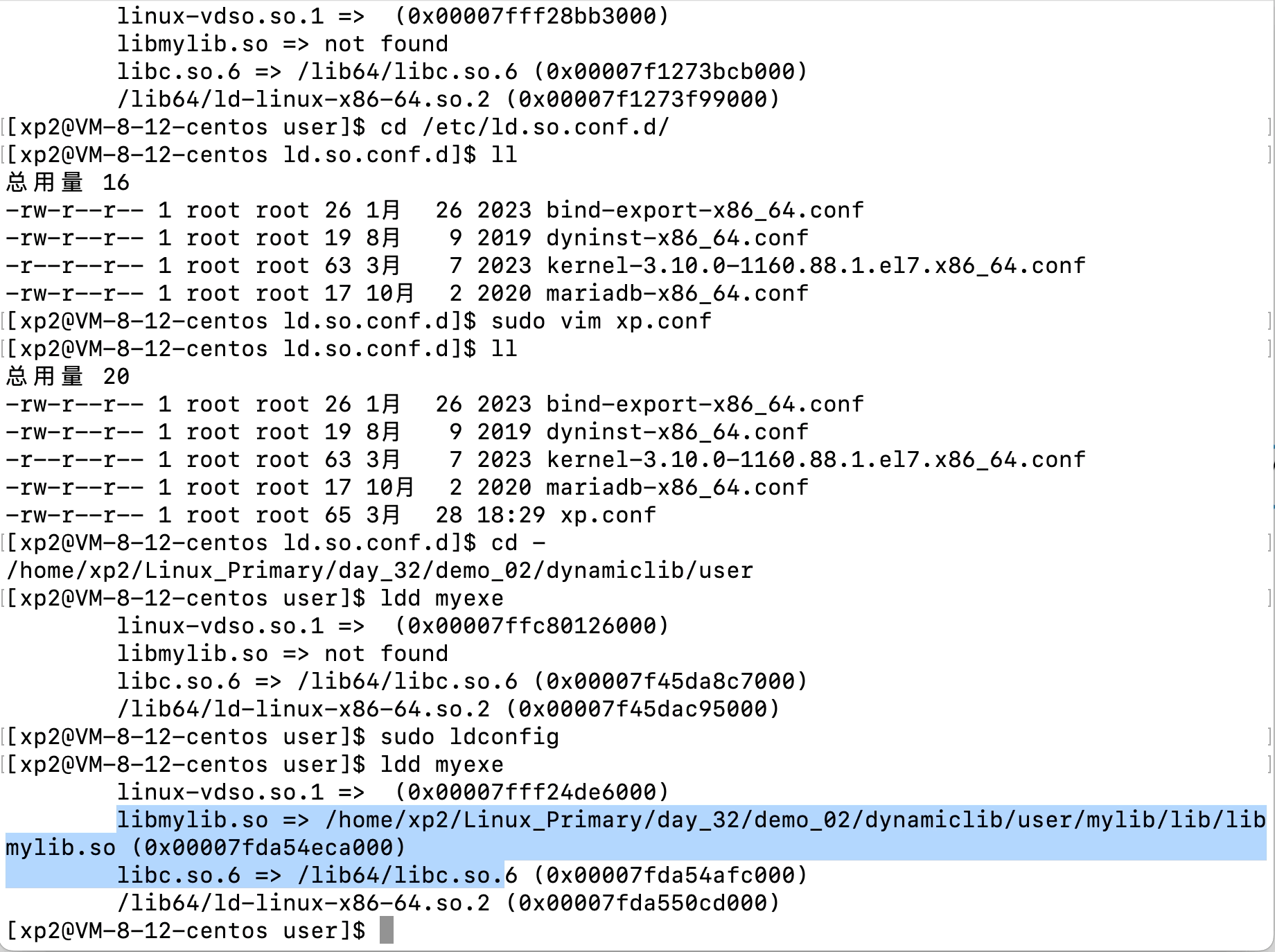
Linux文件(系统)IO(含动静态库的链接操作)
文章目录 Linux文件(系统)IO(含动静态库的链接操作)1、C语言文件IO操作2、三个数据流stdin、stdout、stderr3、系统文件IO3.1、相关系统调用接口的使用3.2、文件描述符fd3.3、文件描述符的分配规则3.3、重定向3.4、自制shell加入重…...
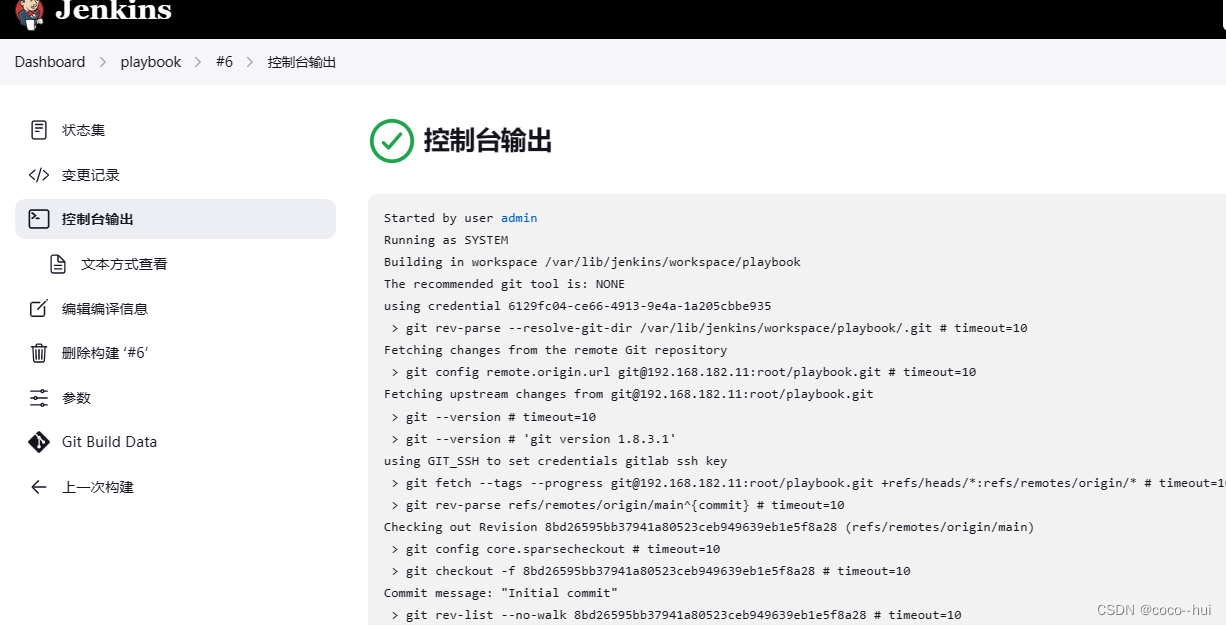
CI/CD实战-jenkins结合ansible 7
配置主机环境 在jenkins上断开并删除docker1节点 重新给master添加构建任务 将server3,server4作为测试主机,停掉其上后面的docker 在server2(jenkins)主机上安装ansible 设置jenkins用户到目标主机的免密 给测试主机创建用户并…...
内网渗透-(黄金票据和白银票据)详解(一)
目录 一、Kerberos协议 二、下面我们来具体分析Kerberos认证流程的每个步骤: 1、KRB_AS-REQ请求包分析 PA-ENC-TIMESTAMP PA_PAC_REQUEST 2、 KRB_AS_REP回复包分析: TGT认购权证 Logon Session Key ticket 3、然后继续来讲相关的TGS的认证过程…...
学习transformer模型-Dropout的简明介绍
Dropout的定义和目的: Dropout 是一种神经网络正则化技术,它在训练时以指定的概率丢弃一个单元(以及连接)p。 这个想法是为了防止神经网络变得过于依赖特定连接的共同适应,因为这可能是过度拟合的症状。直观上&#…...
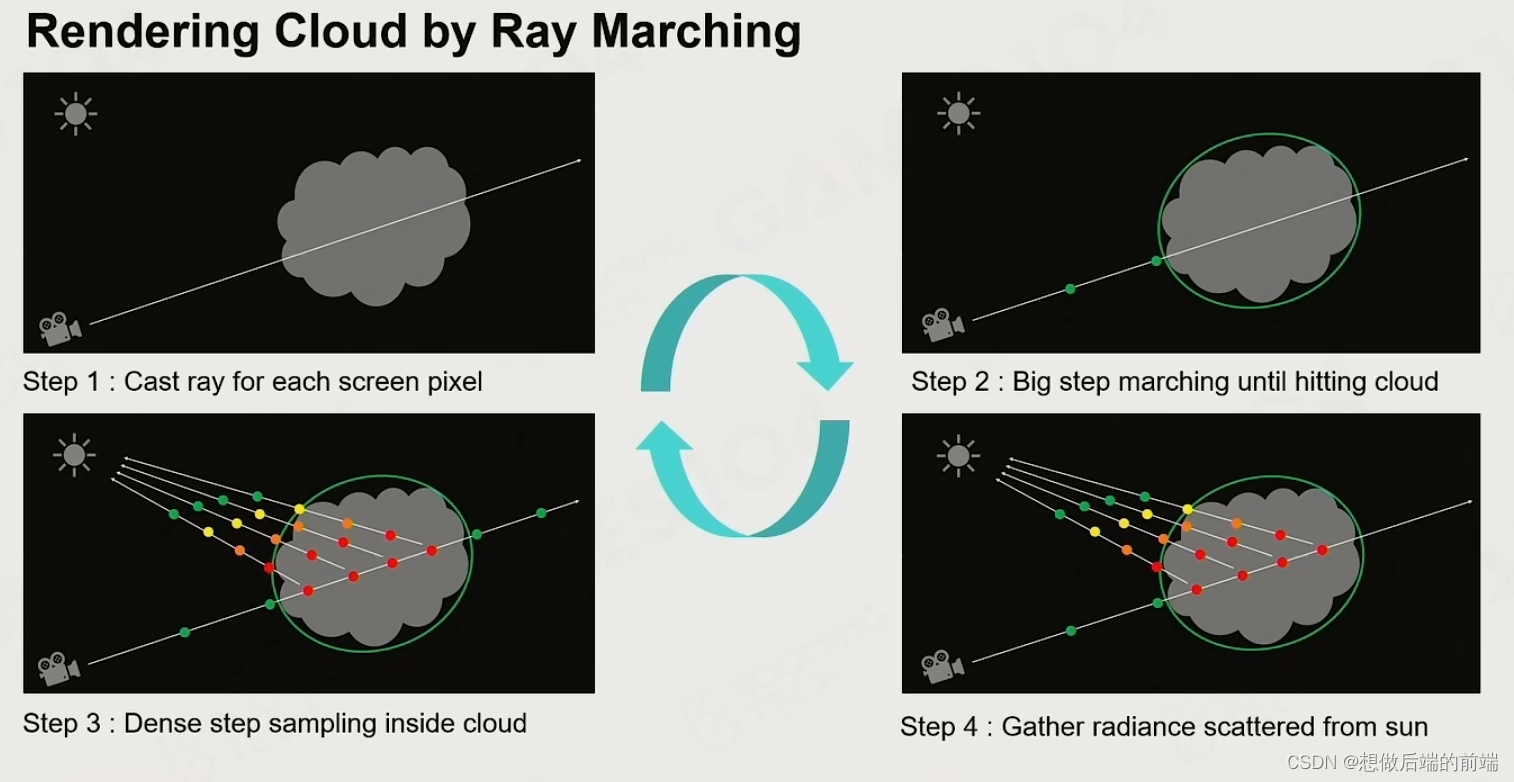
游戏引擎中的大气和云的渲染
一、大气 首先和光线追踪类似,大气渲染也有类似的渲染公式,在实际处理中也有类似 Blinn-Phong的拟合模型。关键参数是当前点到天顶的角度和到太阳的角度 二、大气散射理论 光和介质的接触: Absorption 吸收Out-scattering 散射Emission …...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...
