App推广新篇章:Xinstall助力精准分析与优化
在当前的移动应用市场中,App推广已成为每个开发者不可或缺的一环。然而,推广并非简单的投放广告与等待用户下载,而是需要一套科学、系统的分析与优化流程。这正是Xinstall作为国内专业的App全渠道统计服务商,能够为您带来的核心价值。
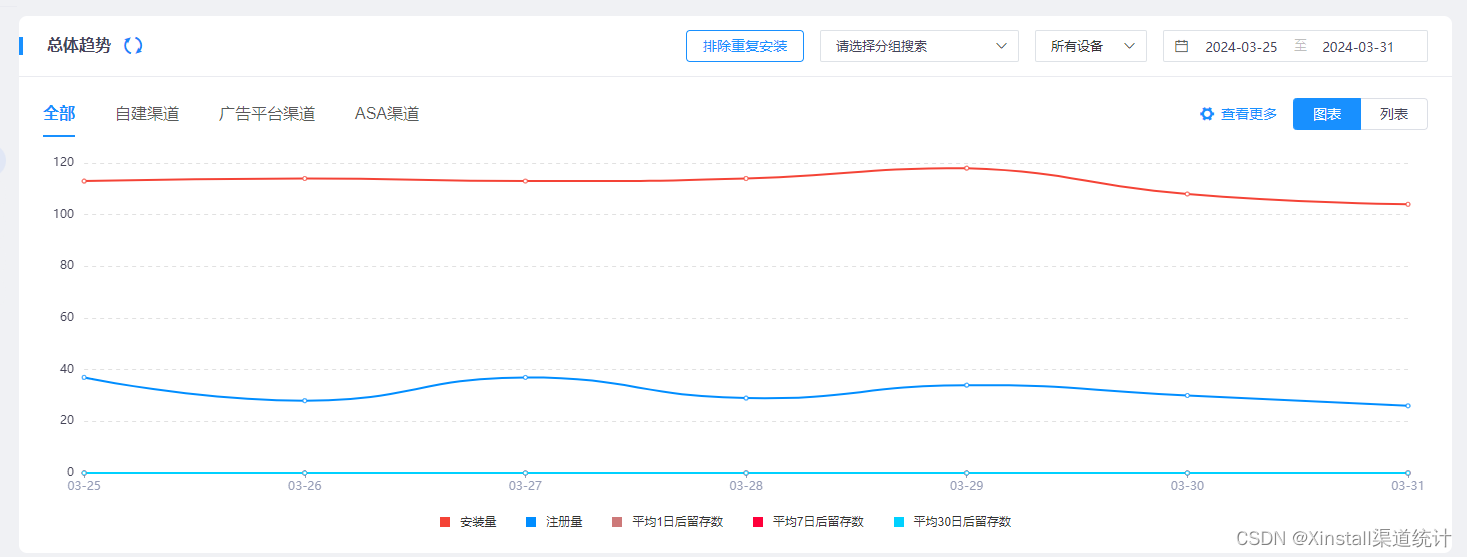
我们知道,App推广的过程中充满了无数的变量与未知,从用户来源、使用习惯到下载转化率,每一个环节都蕴含着丰富的数据与信息。而要想在这海量数据中挖掘出有价值的洞察,就需要一款强大且易用的分析工具。Xinstall正是这样一款工具,它不仅提供了全面的App安装统计服务,更在免填邀请码安装、深度链接一键跳转、携带参数安装等领域有着丰富的服务经验。
使用Xinstall,广告主和开发者能够更清晰地了解推广活动的全貌,从而做出更明智的决策。例如,通过深度链接技术,我们可以追踪用户从哪个渠道、哪个页面进入了App,进而评估不同渠道的推广效果;而通过携带参数安装功能,我们可以更精确地分析用户的行为与偏好,为后续的精准营销提供有力支持。
值得一提的是,Xinstall还具备强大的广告效果监测能力。在这个广告投放日益精细化的时代,能够准确衡量广告效果并持续优化投放策略显得尤为重要。Xinstall的广告效果监测平台不仅能够帮助广告主们更准确地衡量广告投放的效果,还能够挖掘出更多有价值的用户来源和优质的投放渠道。
更重要的是,Xinstall始终以用户体验为优化导向。我们深知,无论推广策略如何精妙,最终都需要落实到用户体验上。因此,我们提供的一站式App全渠道统计服务,始终致力于提升App的渠道效果评估、精准获客能力以及用户体验优化。
App推广的成功离不开科学、系统的分析与优化流程,而Xinstall正是您在这一过程中的得力助手。我们相信,通过Xinstall的专业服务,您将能够更好地洞悉推广效果、衡量广告ROI,从而在激烈的市场竞争中脱颖而出。
相关文章:

App推广新篇章:Xinstall助力精准分析与优化
在当前的移动应用市场中,App推广已成为每个开发者不可或缺的一环。然而,推广并非简单的投放广告与等待用户下载,而是需要一套科学、系统的分析与优化流程。这正是Xinstall作为国内专业的App全渠道统计服务商,能够为您带来的核心价…...

vue知识点: v-if和v-for为何不能同时使用?
在vue2和vue3的官方文档里都写到不推荐 v-if和v-for同时使用,如下代码所示: <li v-for"todo in todos" v-if"!todo.isComplete">{{ todo.text }} </li> 一、vue3文档:列表渲染 | Vue.js 在vue3中ÿ…...
刷题记录)
2024.3.31力扣(1200-1400)刷题记录
一、1523. 在区间范围内统计奇数数目 1.模拟 class Solution:def countOdds(self, low: int, high: int) -> int:# 模拟return len(range(low,high1,2)) if low & 1 else len(range(low1,high1,2)) 2.数学 总结规律。首为偶数就向下取整;奇数就向上取整。…...

【核弹级软安全事件】XZ Utils库中发现秘密后门,影响主要Linux发行版,软件供应链安全大事件
Red Hat 发布了一份“紧急安全警报”,警告称两款流行的数据压缩库XZ Utils(先前称为LZMA Utils)的两个版本已被植入恶意代码后门,这些代码旨在允许未授权的远程访问。 此次软件供应链攻击被追踪为CVE-2024-3094,其CVS…...
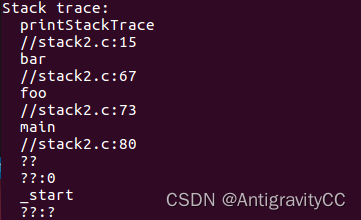
【Linux在程序运行时打印调用栈信息(函数名,文件行号等)】
在程序运行时打印相关调用栈信息(函数名,文件行号等),便于梳理调用逻辑等 //stack.c #include <stdio.h> #include <execinfo.h> #include <stdlib.h> #include <string.h> #include <stdbool.h>#define MAX_…...

9.包和工具【go】
在Go语言中,包是代码的组织单元,而工具链则是Go语言提供的命令行工具,用于构建、测试和调试Go代码。下面我将详细介绍如何导入和使用标准库中的包,如何编写自己的包,以及如何使用Go的工具链。 导入和使用标准库中的包 Go的标准库包含了许多预定义的包,你可以通过导入这…...

判断一个字符串是否是真实手机号:JavaScript
一个简单的正则表达式示例,用于匹配中国大陆的手机号: function isValidPhoneNumber(phoneNumber) {// 定义一个正则表达式,用于匹配中国大陆的手机号const phoneRegex /^1[3-9]\d{9}$/;// 使用正则表达式测试手机号是否匹配return phoneReg…...

3D检测:从pointnet,voxelnet,pointpillar到centerpoint
记录centerpoint学习笔记。目前被引用1275次,非常高。 地址:Center-Based 3D Object Detection and Tracking (thecvf.com) GitHub - tianweiy/CenterPoint CenterPoint:三维点云目标检测算法梳理及最新进展(CVPR2021ÿ…...

使用canvas内置api完成图片的缩放平移和导出和添加提示
最近挺忙的,几乎没有时间去更新博客,今天正好在学习新东西,正好和大家分享一下。 最近要做一个使用canvas完成图片平移,缩放,添加标注的需求,完成的效果大概如下: 使用canvas内置api完成图片的缩…...
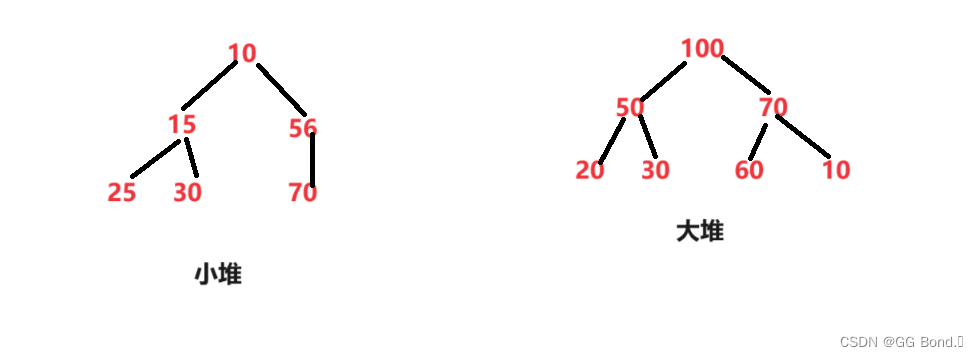
数据结构——二叉树——堆
前言: 在前面我们已经学习了数据结构的基础操作:顺序表和链表及其相关内容,今天我们来学一点有些难度的知识——数据结构中的二叉树,今天我们先来学习二叉树中堆的知识,这部分内容还是非常有意思的,下面我们…...
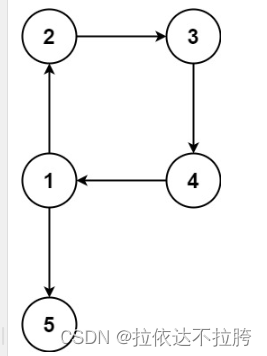
算法学习——LeetCode力扣图论篇3(127. 单词接龙、463. 岛屿的周长、684. 冗余连接、685. 冗余连接 II)
算法学习——LeetCode力扣图论篇3 127. 单词接龙 127. 单词接龙 - 力扣(LeetCode) 描述 字典 wordList 中从单词 beginWord 和 endWord 的 转换序列 是一个按下述规格形成的序列 beginWord -> s1 -> s2 -> … -> sk: 每一对相…...

状态模式详解:管理对象状态的利器
在软件设计中,我们经常会遇到需要根据对象的不同状态来执行不同行为的情况。为了优雅地管理这些状态及其对应的行为,状态模式(State Pattern)应运而生。本文将深入探讨状态模式的使用条件、Java代码实现,并结合现实社会…...

探索----------------阿里云
目录 一、阿里云四大件 1、云服务器ECS 2、云数据库RDS 3、负载均衡SLB 4、对象存储OSS 5、其他的云计算产品 1)内容分发网络CDN 2)专有网络 VPC 二、linux发行版本 三、你平时对系统会怎么优化(五大负载) 1、cpu 使用率…...
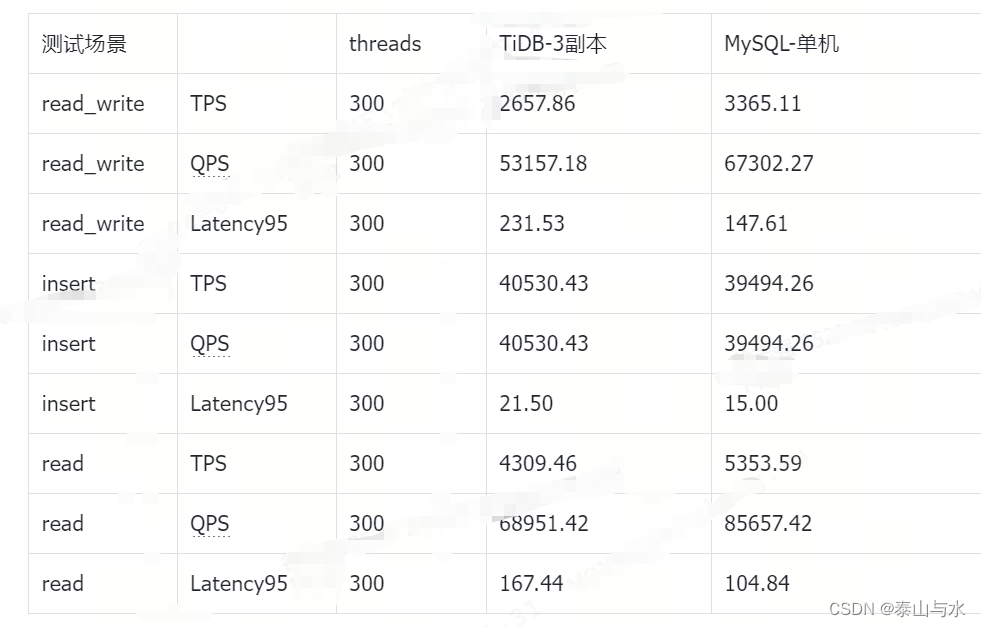
Tidb和MySQL性能简单测试对比
一、单SQL性能对比 由于TiDB的并发能力优秀,但是单个SQL执行延迟较差,为了客观对比,所以只用1个线程来压测tidb和mysql,以观察延迟情况 二、并发SQL性能对比 TiDB:v6.5.2 MySQL:8.0.26 (单机) 三、结论 …...

2024.2.6力扣每日一题——魔塔游戏
2024.2.6 题目来源我的题解方法一 贪心优先队列 题目来源 力扣每日一题;题序:LCP 30 我的题解 方法一 贪心优先队列 思路:使用贪心的思想,从左到右遍历,若遇到加上当前房间的生命值后小于等于0,由于需要…...

C# OAuth单点登录的实现
原理 单点登录(Single Sign-On,简称SSO)是一种身份验证技术,它允许用户使用一组凭据(如用户名和密码)登录多个相关但独立的系统,而无需在每个系统中都进行登录操作。下面是一个简单的SSO实现示…...

AtCoder Beginner Contest 347 (ABCDEF题)视频讲解
A - Divisible Problem Statement You are given positive integers N N N and K K K, and a sequence of length N N N, A ( A 1 , A 2 , … , A N ) A(A_1,A_2,\ldots,A_N) A(A1,A2,…,AN). Extract all elements of A A A that are multiples of K K K, divi…...
【vue2+antvx6】报错Cannot read properties of undefined (reading ‘toUpperCase‘)
我的代码是这样的 <el-collapseref"collapse"v-model"active"accordionclass"collapseStart"change"collapsechange"><el-collapse-item:name"String(index 1)"v-for"(i, index) in List":key"in…...

主流的开发语言、环境及其特点
主流的开发语言及其特点: 1. Python:以其简洁的语法和强大的库支持而闻名,适用于数据科学、人工智能和网络开发等领域。 2. Java:跨平台的编程语言,广泛应用于企业级应用、Android 开发和大型系统开发。 3. C…...

Android知识 - 代码混淆ProGuard规则介绍
ProGuard 的规则及示例 规则概述 ProGuard 是一个代码优化工具,它通过移除未使用的代码、重命名类、字段和方法等方式来减小应用的大小。在 ProGuard 的配置文件中,我们可以定义一系列的规则来控制优化和混淆的过程。 规则语法 ProGuard 的规则通常包…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...
