当前位置： 首页 > news >正文

马斯克旗下xAI发布Grok-1.5，相比较开源的Grok-1，各项性能大幅提升，接近GPT-4！

news 2026/2/11 0:17:32

本文原文来自DataLearnerAI官方网站：马斯克旗下xAI发布Grok-1.5，相比较开源的Grok-1，各项性能大幅提升，接近GPT-4！ | 数据学习者官方网站(Datalearner)

继Grok-1开源之后，xAI宣布了Grok-1.5的内测消息，并预告即将全面商用，这一消息无疑为AI技术爱好者和开发者社区带来了新的兴奋点。

Grok-1.5的技术突破

Grok-1.5在性能上的提升是显著的。根据官方发布的数据，Grok-1.5在综合理解能力MMLU评测上达到了81.3分，超越了MistralAI的Mixtral Large模型。在数学推理能力GSM8K的评测中，Grok-1.5更是取得了90分的高分，与业界领先的GPT-4和Claude-3 Sonnet相差无几。

Grok-1.5在DataLearnerAI综合评测排行

在DataLearnerAI收集的全球大模型综合评测数据上，Grok-1.5表现也非常好。按照GSM8K排序，结果如下：

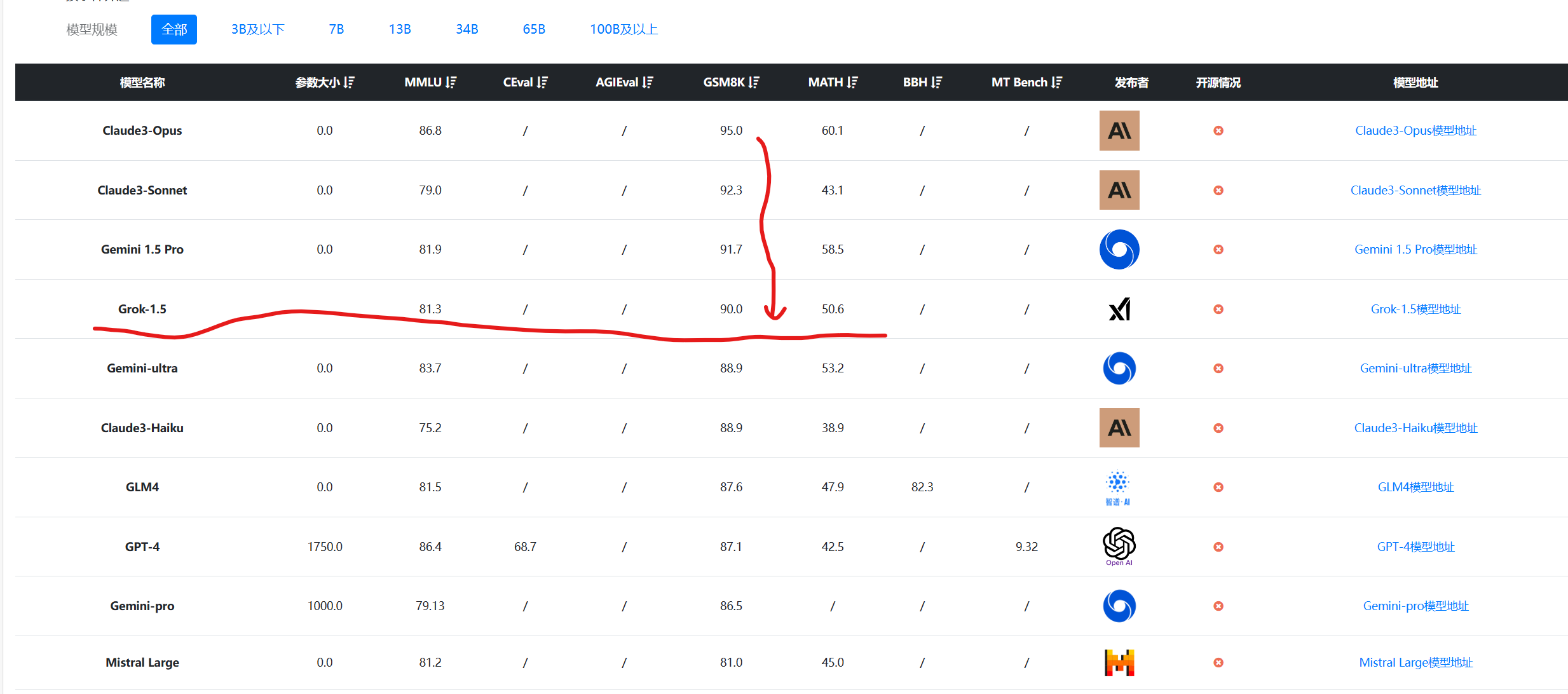
数据来源：大模型综合评测对比 | 当前主流大模型在各评测数据集上的表现总榜单 | 数据学习 (DataLearner)

可以看到，GSM8K在目前的评测上，Grok-1.5已经是全球第四，最好的模型之一了。其它评测结果也是类似，说明Grok-1.5已经达到了第一梯队。而按照编程能力评测的结果，以Human Eval排序为例，结果如下：

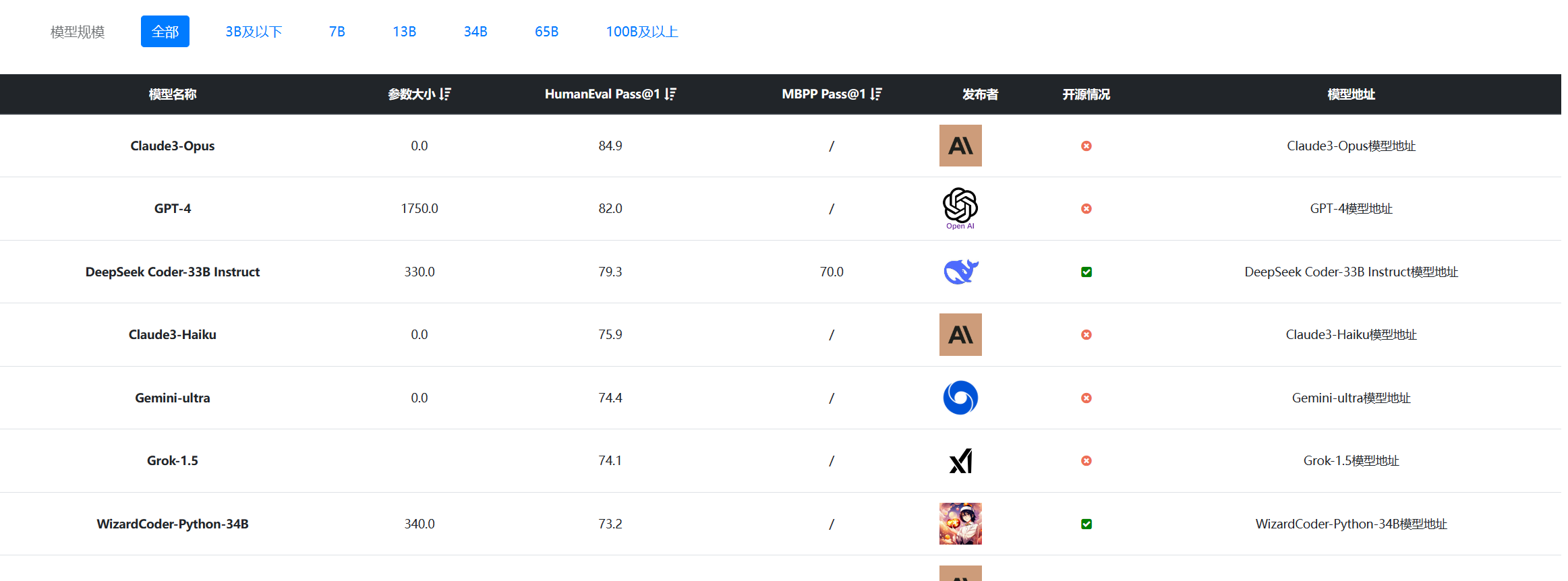
数据来源：大模型代码能力评测对比 | 当前主流大模型在代码能力上的表现总榜单 | 数据学习 (DataLearner)

可以看到，Grok-1.5依然排名很高，作为一个综合基础大模型，这样的成绩非常好。略超Claude3-Sonnet！

支持128K上下文长度

Grok-1.5的另一个亮点是支持最高128K的上下文长度，这是第一代Grok-1的8K上下文长度的显著提升。在大海捞针测试中，Grok-1.5表现出色，这一特性对于处理长文本和复杂对话场景具有重要意义。

关于Grok-1.5的详情参考DataLearnerAI原文：马斯克旗下xAI发布Grok-1.5，相比较开源的Grok-1，各项性能大幅提升，接近GPT-4！ | 数据学习者官方网站(Datalearner)

相关文章：

马斯克旗下xAI发布Grok-1.5，相比较开源的Grok-1，各项性能大幅提升，接近GPT-4！

本文原文来自DataLearnerAI官方网站：马斯克旗下xAI发布Grok-1.5，相比较开源的Grok-1，各项性能大幅提升，接近GPT-4！ | 数据学习者官方网站(Datalearner) 继Grok-1开源之后，xAI宣布了Grok-1.5的内测消息&…...

编程日记 2024/4/2 7:13:37

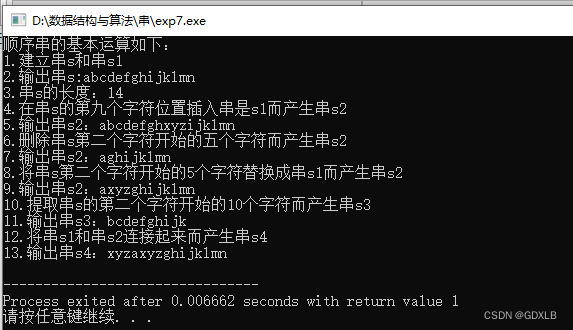
数据结构与算法 顺序串的基本运算

一、实验内容 编写一个程序sqstring.cpp，实现顺序串的各种基本运算，并在此基础上实现一个程序exp7.cpp，完成以下功能： （1）建立串s“abcdefghefghijklmn”和串s1“xyz” （2）输出串…...

编程日记 2024/4/2 7:12:36

2024年04月数据库流行度最新排名

点击查看最新数据库流行度最新排名（每月更新） 2024年04月数据库流行度最新排名 TOP DB顶级数据库索引是通过分析在谷歌上搜索数据库名称的频率来创建的 一个数据库被搜索的次数越多，这个数据库就被认为越受欢迎。这是一个领先指标。原始数…...

编程日记 2024/4/2 7:10:34

golang语言系列：SOLID、YAGNI、KISS等设计原则

云原生学习路线导航页（持续更新中） 本文是 golang语言系列 文章，主要对编程通用技能 SOLID、YAGNI、KISS等设计原则 进行学习 1.SOLID设计原则 S：SRP，单一职责原则O：OCP，开闭原则L：…...

编程日记 2024/4/2 7:08:32

Meta Pixel：助你实现高效地Facebook广告追踪

Meta Pixel 像素代码是用來衡量Facebook广告效果的一个官方数据工具，只要商家有在Facebook上投放广告就需要串联Meta Pixel 像素代码来查看相关数据。 它本质上是一段 JavaScript 代码，安装后可以让用户在自己网站上查看到访客活动。它的工作原理是加载…...

编程日记 2024/4/2 7:07:31

基于Arduino IDE 野火ESP8266模块 文件系统LittleFS 的开发

一、文件系统LittleFS的介绍 LittleFS是一个为微控制器设计的轻量级、可靠且高性能的文件系统。它专为嵌入式设备打造，拥有占用空间小、对硬件要求低的特点，同时保证在断电情况下数据的完整性和稳定性。 1.设计与特点 LittleFS的设计旨在提供嵌入式系统所…...

编程日记 2024/4/2 7:04:28

通讯录改造———文件版本

上一篇文章我们详细讲了文件操作，这时候我们就可以把通讯录保存到文件中，这样即使程序退出了，联系人的信息也还是保存着，下一次启动程序时我们就可以把文件中的数据读取到程序中来使用。 保存 首先我们要在退出通讯录之前把联系人…...

编程日记 2024/4/2 7:01:26

FastAPI Web框架教程 第13章 WebSocket

13-1 WebSocket是什么 WebSocket简介： WebSocket是一种在单个TCP连接上进行全双工通信的协议。 WebSocket使得客户端和服务器之间的数据交换变得更加简单，允许服务端主动向客户端推送数据。 在WebSocket API中，浏览器和服务器只需要完成一…...

编程日记 2024/4/2 6:57:21

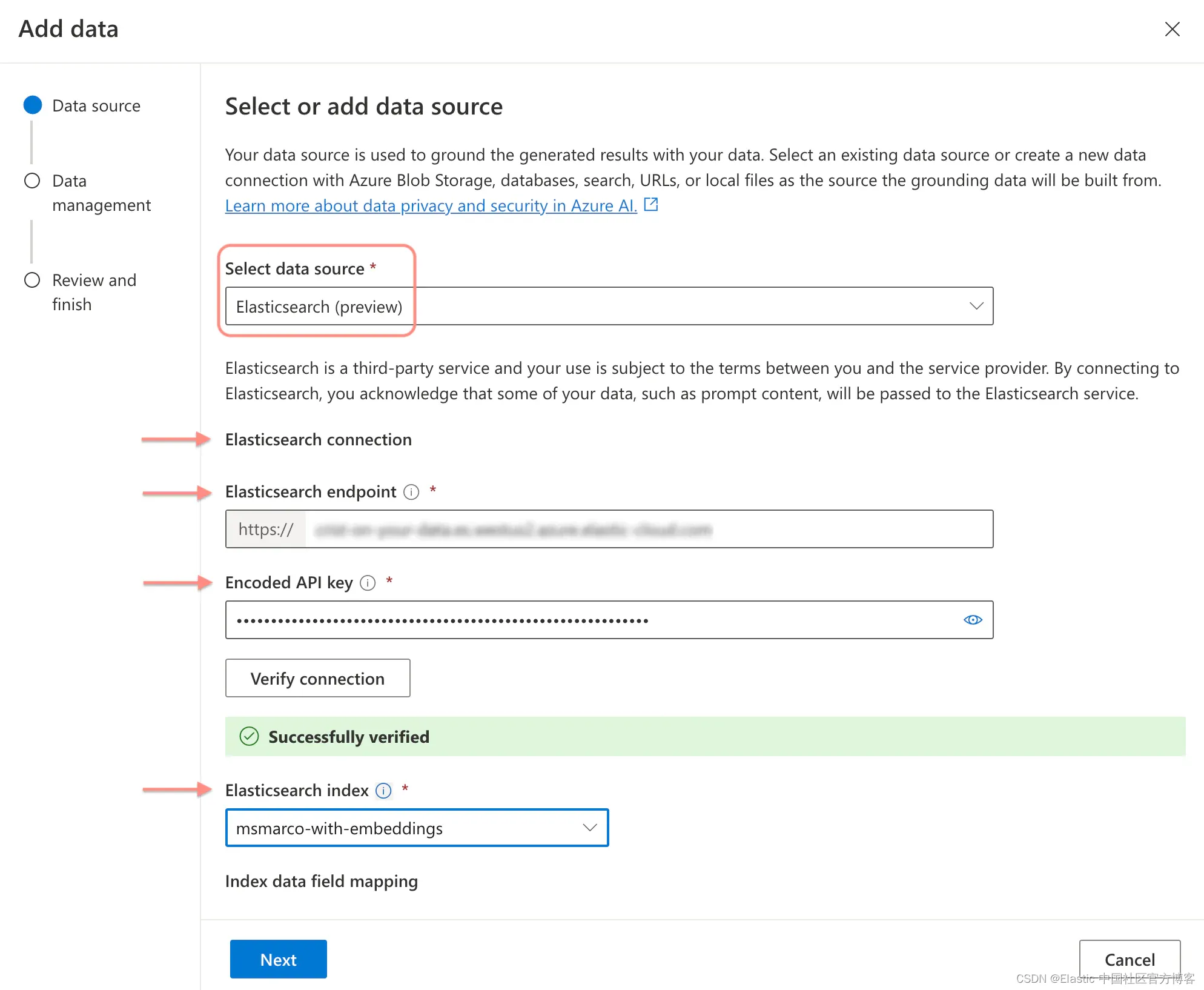
将 Elasticsearch 向量数据库引入到数据上的 Azure OpenAI 服务（预览）

作者：来自 Elastic Aditya Tripathi Microsoft 和 Elastic 很高兴地宣布，全球下载次数最多的向量数据库 Elasticsearch 是公共预览版中 Azure OpenAI Service On Your Data 官方支持的向量存储和检索增强搜索技术。 这项突破性的功能使你能够利用 GPT-4 …...

编程日记 2024/4/2 6:54:18

SeLinux 常见的宏

在SeLinux框架中，google定义好了一些宏，我们使用这些宏，开发时可以更加方便。大部分的宏是定义在te_macros文件中 type_transition type_transition source_type target_type : class default_type当主体进程域source_type 对target_type 类…...

编程日记 2024/4/2 6:53:17

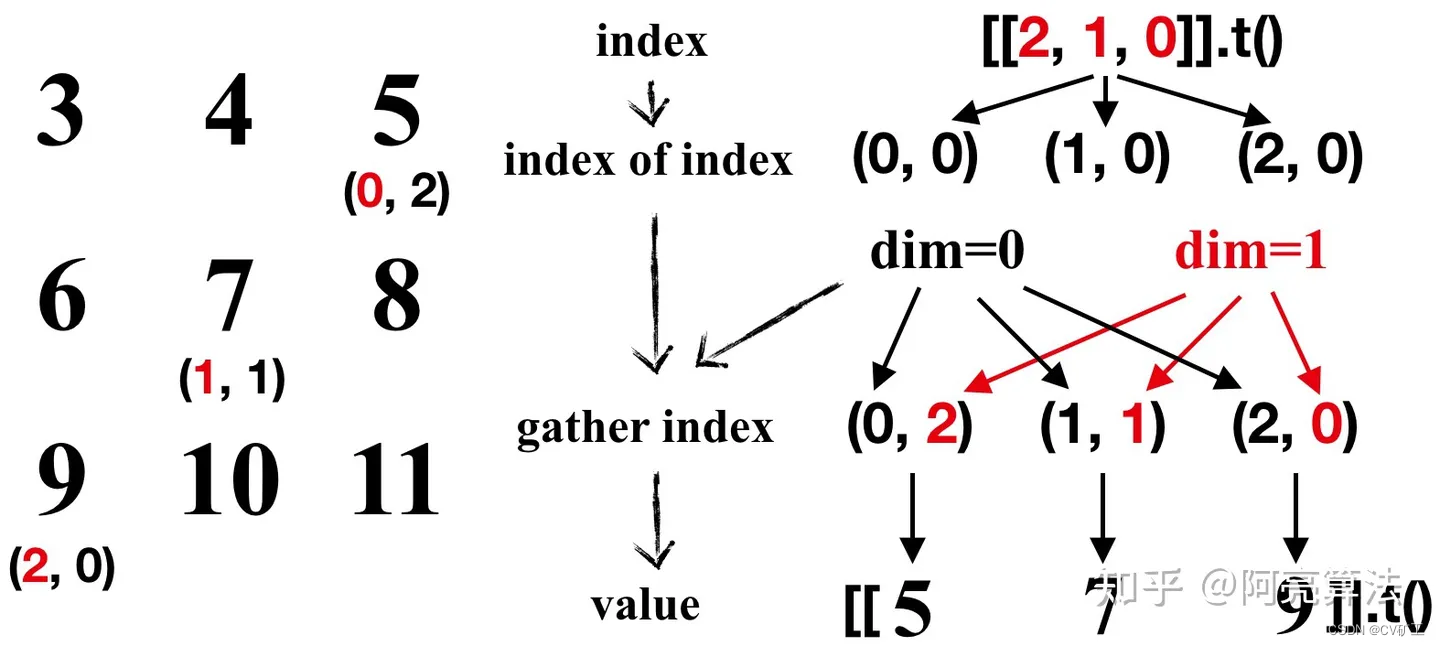
图解PyTorch中的torch.gather函数和 scatter 函数

前言 torch.gather在目前基于 transformer or query based 的目标检测中，在最后获取目标结果时，经常用到。 这里记录下用法，防止之后又忘了。 介绍 torch.gather 官方文档对torch.gather()的定义非常简洁 定义：从原tensor中获…...

编程日记 2024/4/2 6:52:16

Pytorch实用教程： torch.tensor()的用法

在PyTorch中，torch.tensor()函数是用来创建张量（Tensor）的一个非常基础和重要的函数。张量是PyTorch中的基本数据结构，用于存储和操作数据，可以看作是一个高维数组。torch.tensor()函数可以从数据创建新的张量&#xf…...

编程日记 2024/4/2 6:51:15

Java设计模式详解：工厂模式

Java设计模式详解：工厂模式 文章目录 Java设计模式详解：工厂模式前言一、工厂模式是个啥？二、工厂模式怎么用？三、工厂模式啥时候用？四、工厂模式的优点总结 前言 今天咱们来聊聊设计模式中的一位重要成员——工厂模式…...

编程日记 2024/4/2 6:50:14

Python爬虫：爬虫常用伪装手段

目录 前言 一、设置User-Agent 二、设置Referer 三、使用代理IP 四、限制请求频率 总结 前言 随着互联网的快速发展，爬虫技术在网络数据采集方面发挥着重要的作用。然而，由于爬虫的使用可能会对被爬取的网站造成一定的压力，因此&#…...

编程日记 2024/4/2 6:48:12

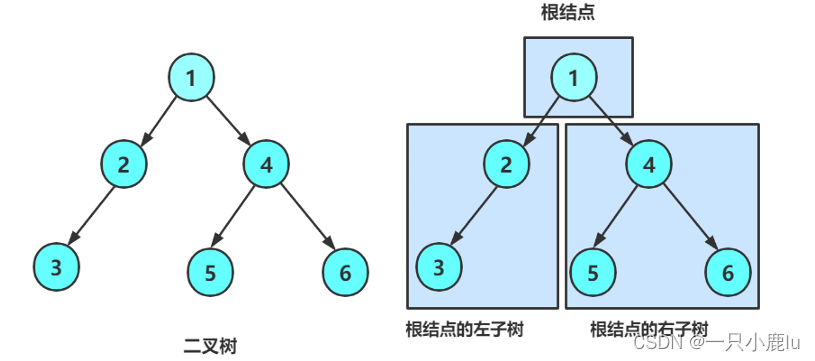
【数据结构】非线性结构---二叉树

1、树 1.1 树的相关概念 节点的度：一个节点含有的子树的个数称为该节点的度； 如上图：A的为6 叶节点或终端节点：度为0的节点称为叶节点； 如上图：B、C、H、I...等节点为叶节点 非终端节点或分支节点&#…...

编程日记 2024/4/2 6:47:11

【战略前沿】与中国达成生产协议后，飞行汽车即将起飞

【原文】Flying cars edge towards takeoff after Chinese production deal 【作者】Thomas Macaulay 斯洛伐克公司KleinVision签署了一项协议，将大规模生产AirCar。 一辆获得航空认证的飞行汽车向商业化又迈出了一大步。 空中汽车的创造者KleinVision今天宣布出售…...

编程日记 2024/4/2 6:46:10

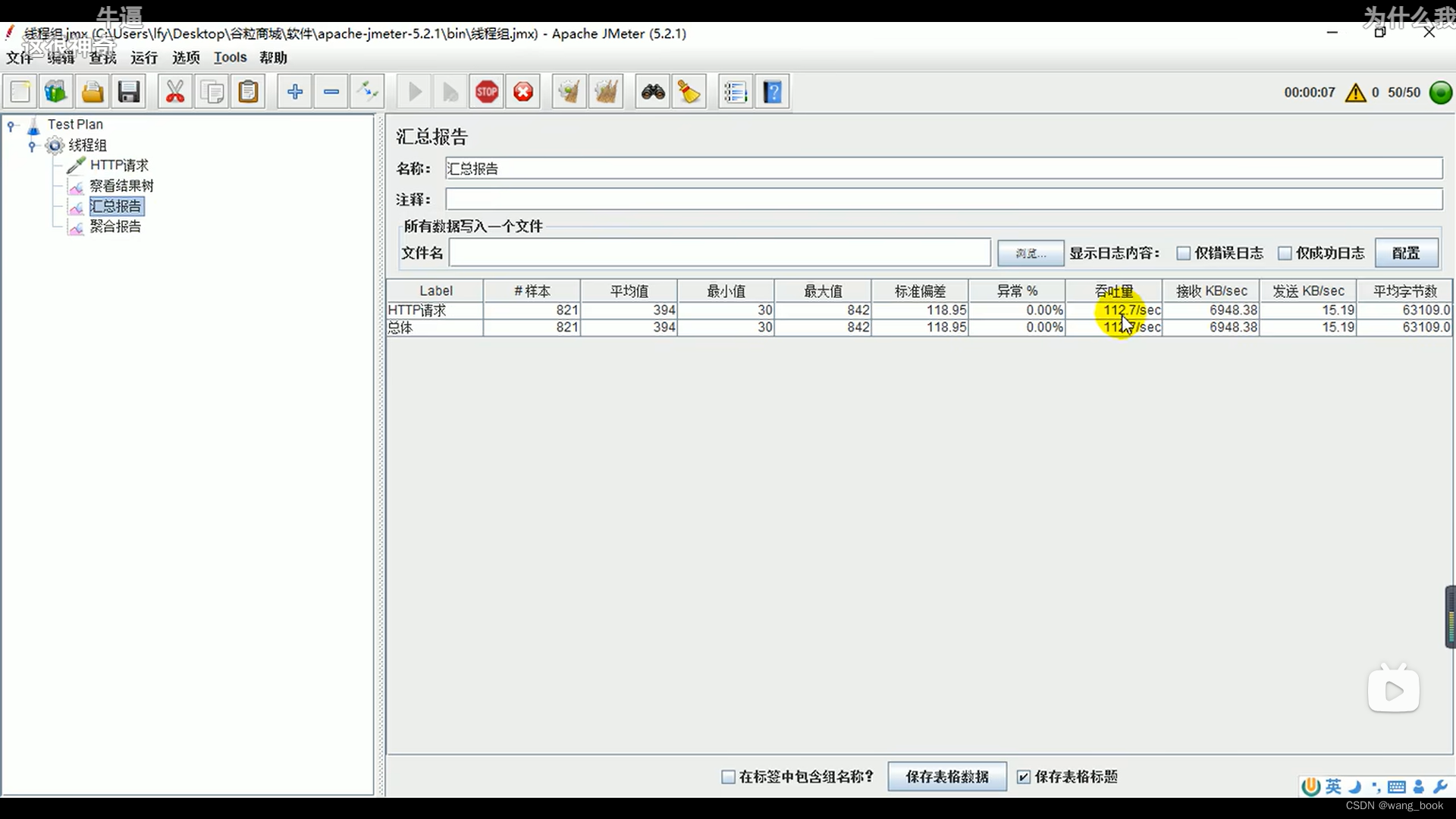
谷粒商城实战(007 压力测试)

Java项目《谷粒商城》架构师级Java项目实战，对标阿里P6-P7，全网最强 总时长 104:45:00 共408P 此文章包含第141p-第p150的内容 简介 安装jmeter 安装jmeter 使用中文 这样写就是200个线程循环100次 一共是2万个请求 介绍线程组 添加请求 可以是htt…...

编程日记 2024/4/2 6:44:08

使用CSS计数器，在目录名称前加上了序号，让目录看起来更加井然有序

目录（Text of Contents缩写为TOC），其实就是一篇文章的概要或简述。这好比，去书店买书，先是被这本书的标题所吸引，而后我们才会，翻开这本书目录，看看这本书主要是在讲些什么&#xff…...

编程日记 2024/4/2 6:43:07

SSH常见运维总结

1 -bash: ssh: command not found 解决办法："yum install －y openssh-server openssh-clinets" 2 ssh登录时提示：Read from socket failed: Connection reset by peer. 原因：/etc/ssh/下没有ssh*key*文件 解决&…...

编程日记 2024/4/2 6:41:05

uni app 扫雷

闲来无聊。做个扫雷玩玩吧&#xff0c;点击打开&#xff0c;长按标记&#xff0c;标记的点击两次或长按取消标记。所有打开结束 <template><view class"page_main"><view class"add_button" style"width: 100vw; margin-bottom: 20r…...

编程日记 2024/4/2 6:39:03

地震勘探——干扰波识别、井中地震时距曲线特点

目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波&#xff1a;可以用来解决所提出的地质任务的波&#xff1b;干扰波&#xff1a;所有妨碍辨认、追踪有效波的其他波。 地震勘探中&#xff0c;有效波和干扰波是相对的。例如&#xff0c;在反射波…...

编程新知 2026/2/8 20:43:05

Java - Mysql数据类型对应

Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

编程新知 2025/12/14 11:45:25

苍穹外卖--缓存菜品

1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得&#xff0c;如果用户端访问量比较大&#xff0c;数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据&#xff0c;减少数据库查询操作。 缓存逻辑分析&#xff1a; ①每个分类下的菜品保持一份缓存数据…...

编程新知 2026/2/7 15:39:49

蓝桥杯3498 01串的熵

问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798&#xff0c; 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

编程新知 2026/2/6 2:05:50

USB Over IP专用硬件的5个特点

USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中&#xff0c;从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备&#xff08;如专用硬件设备&#xff09;&#xff0c;从而消除了直接物理连接的需要。USB over IP的…...

编程新知 2026/2/6 13:42:22

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战

说明&#xff1a;这是一个机器学习实战项目&#xff08;附带数据代码文档&#xff09;&#xff0c;如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下&#xff0c;风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

编程新知 2026/2/9 17:44:07

使用LangGraph和LangSmith构建多智能体人工智能系统

现在&#xff0c;通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战&#xff0c;比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

编程新知 2026/1/26 13:48:59

MFC 抛体运动模拟：常见问题解决与界面美化

在 MFC 中开发抛体运动模拟程序时，我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点，详细解析原因并提供解决方案，同时兼顾界面美化，让模拟效果更专业、更高效。 问题一：历史轨迹与小球残影残留 现象 小球运动后，历史位置的 “残影”…...

编程新知 2026/1/29 12:12:12

在Mathematica中实现Newton-Raphson迭代的收敛时间算法（一般三次多项式）

考察一般的三次多项式&#xff0c;以r为参数&#xff1a; p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]&#xff1b; 此多项式的根为&#xff1a; 尽管看起来这个多项式是特殊的&#xff0c;其实一般的三次多项式都是可以通过线性变换化为这个形式…...

编程新知 2026/1/30 3:24:00

脑机新手指南（七）：OpenBCI_GUI：从环境搭建到数据可视化（上）

一、OpenBCI_GUI 项目概述 &#xff08;一&#xff09;项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台&#xff0c;其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言&#xff0c;首次接触 OpenBCI 设备时&#xff0c;往…...

编程新知 2026/2/3 4:26:32