(九)关系数据理论

- 函数依赖:设R(U)是属性集U上的关系模式。X、Y是属性集U的子集。若对于R(U)的任意一个可能的关系r,r中不可能存在两个元组在X上的属性值相等,而在Y上的属性值不等,则称X函数确定Y或Y函数依赖于X,记作X→Y。(即只要X 上的属性值相等,Y上的值一定相等)。
- 完全函数依赖:(full)在R(U)中,如果X→Y,并且对于X 的任何一个真子集X',都有
 ,则称Y对X完全函数依赖,记作
,则称Y对X完全函数依赖,记作 。(即只要X删去一个属性,就不再决定Y,即为完全函数依赖)
。(即只要X删去一个属性,就不再决定Y,即为完全函数依赖) - 部分函数依赖:(partial)若X→Y,但Y不完全函数依赖于X,则称Y 对X 部分函数依赖,记作:

- 传递函数依赖:在R(U)中,如果
 则称Z对X传递函数依赖。(即只要两个依赖关系中的三个属性组不互相完全包含,Y对X不函数依赖,Z对X不函数依赖,就构成传递函数依赖)
则称Z对X传递函数依赖。(即只要两个依赖关系中的三个属性组不互相完全包含,Y对X不函数依赖,Z对X不函数依赖,就构成传递函数依赖) - 候选码:设K为R<U,F>中的属性或属性组合,若
 ,则K为R的候选码。
,则K为R的候选码。 - 主码:若候选码多于一个,则选定其中的一个为主码。
- 外码:关系模式R中属性或属性组X并非是R的码,但X是另一个关系模式的码,则称X是R的外部码,也称外码。
- 全码:整个属性组是码,称为全码。
- 主属性:包含在某一候选码中的一个属性称为主属性。
- 非主属性:不包含在任一候选码中的一个属性。也即除主属性外的其他属性称为非主属性。
- 超键: 在关系中能唯一标识元组的属性集称为关系模式的超键,可以包含非主属性。
- 1NF:关系模式R 的每一个分量是不可再分的数据项。 (即关系模式最起码的要求)
- 2NF:关系模式R∈1NF,且每一个非主属性完全函数依赖于码,(即进一步消除了非主属性对候选码的部分函数依赖。)
- 3NF:关系模式R<U,F>中不存在这样的码X、属性组Y及非主属性A,且
 ,则符合第三范式。(即进一步消除了非主属性对侯选码的传递函数依赖)
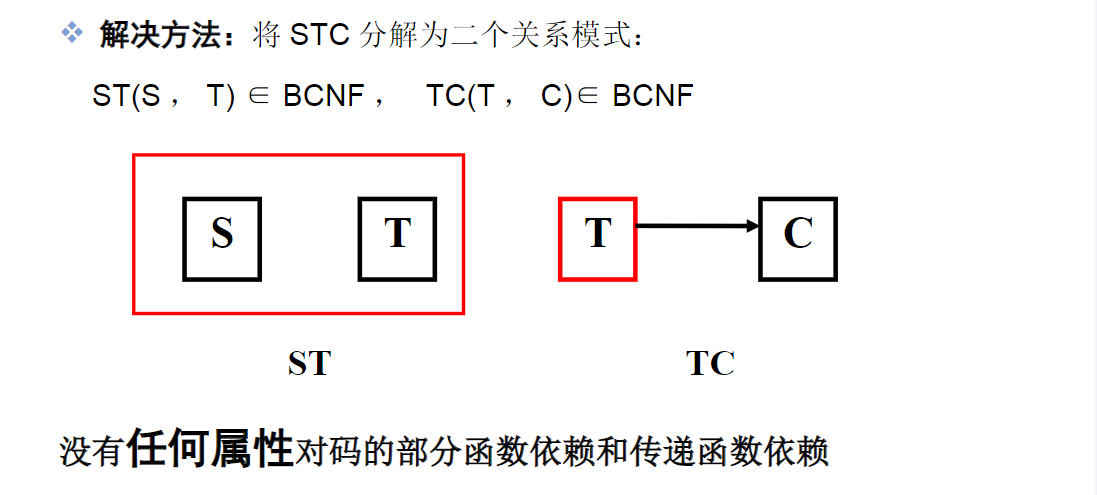
,则符合第三范式。(即进一步消除了非主属性对侯选码的传递函数依赖) - BCNF:关系模式 R<U,F> ∈ 1NF, X→Y且Y不是X的子集时,X必含候选码。即没有不依赖于候选键的函数依赖存在。(即进一步消除了主属性对候选码的部分和传递函数依赖)
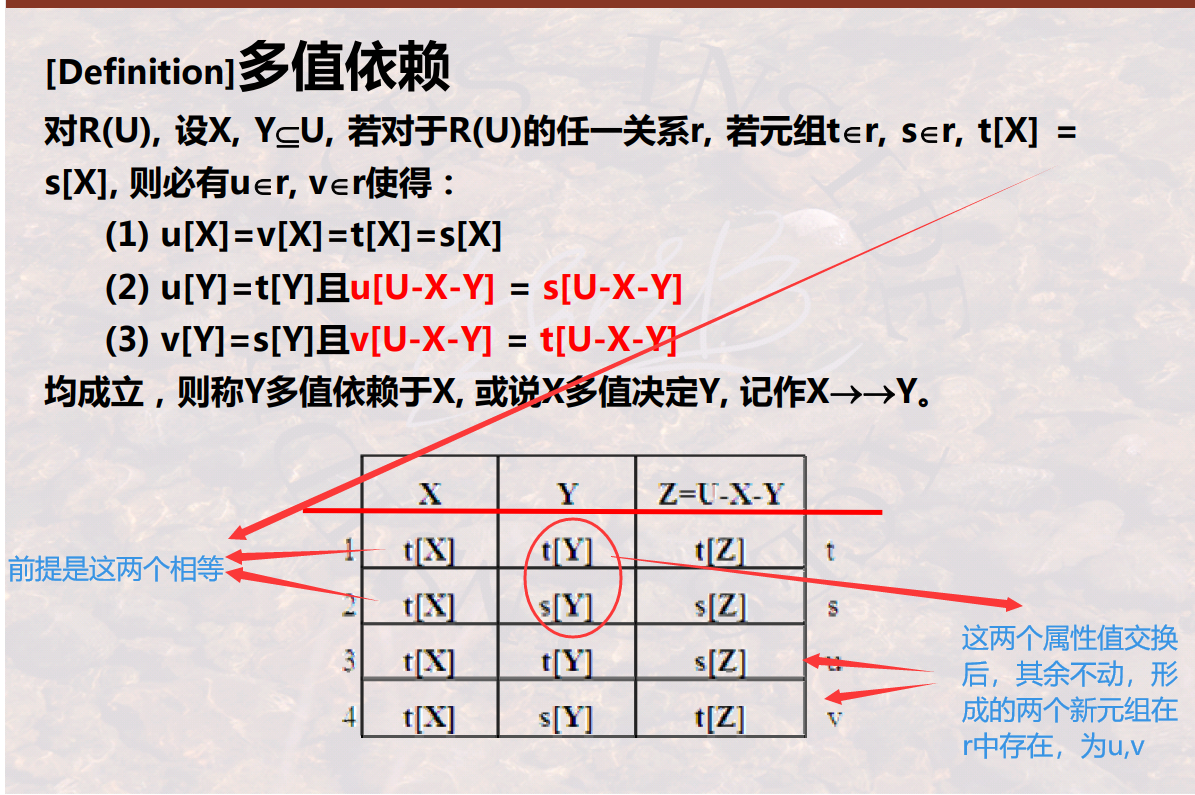
- 多值依赖:设R(U)是属性集U上的一个关系模式。X,Y,Z是U的子集,并且关系模式R(U)中多值依赖x→→y成立,当且仅当对R(U)的任一关系r,给定的一对(x,z)值,有一组y的值,这组值仅仅决定于X值而与Z值无关。
- 4NF:关系模式每如果对于R 的每个非平凡多值依赖X→→Y(Y不是X 的子集,Z=U-X-Y不为空),X 都含有码。 (即进一步消除了非主属性对候选键以外属性的多值依赖)
- 逻辑蕴涵:设F是关系模式R(U)中的一个函数依赖集合,X, Y是R的属性子集,如果从F中的函数依赖能够推导出X→Y,则称F逻辑蕴涵X→Y, 或称X→Y是F的逻辑蕴涵。
- 闭包:被F逻辑蕴涵的所有函数依赖集合称为F的闭包(Closure),记作 F+。 说明:若F+=F, 则说F是一个全函数依赖族(函数依赖完备集)。




9.1问题的提出




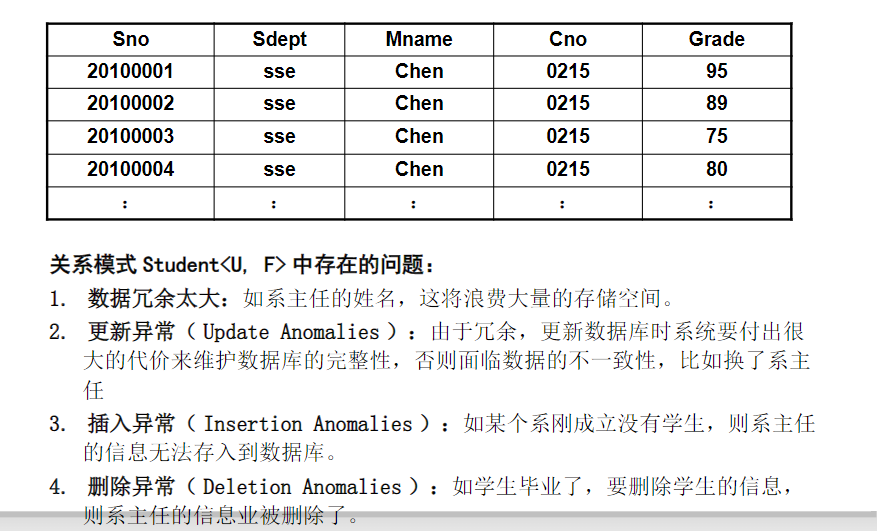

9.2规范化理论
9.2.1函数依赖




不能消去任何属性的决定因素,符合完全函数依赖。




9.2.2范式


1NF

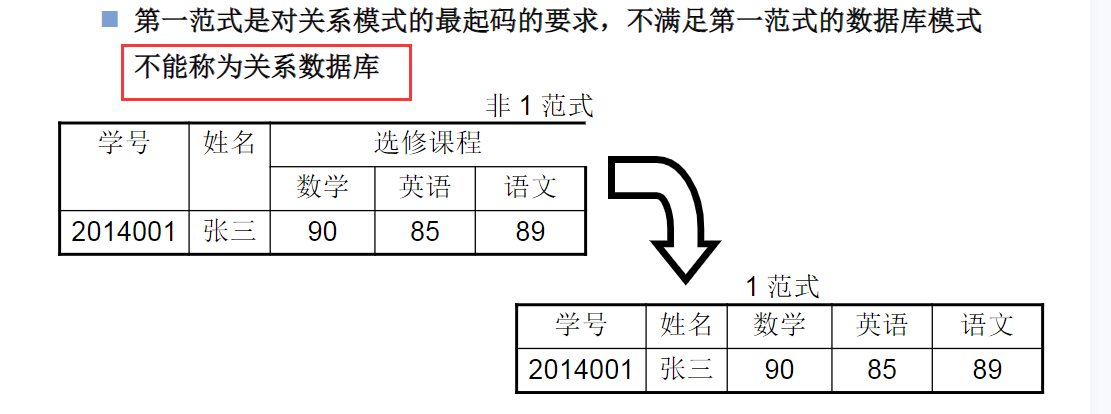
2NF


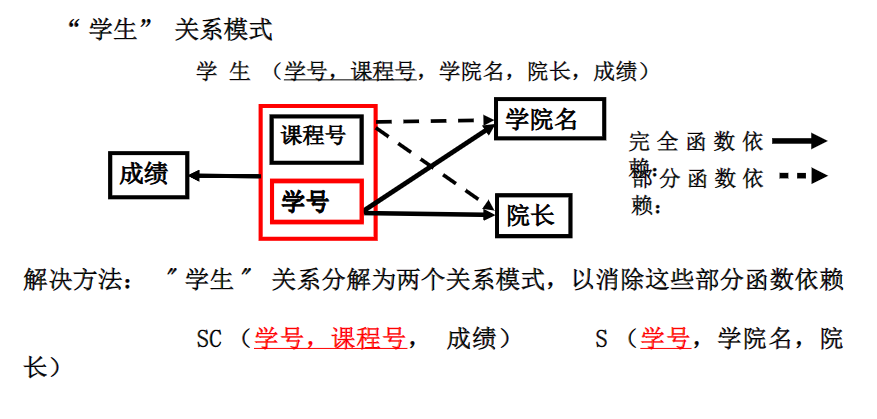
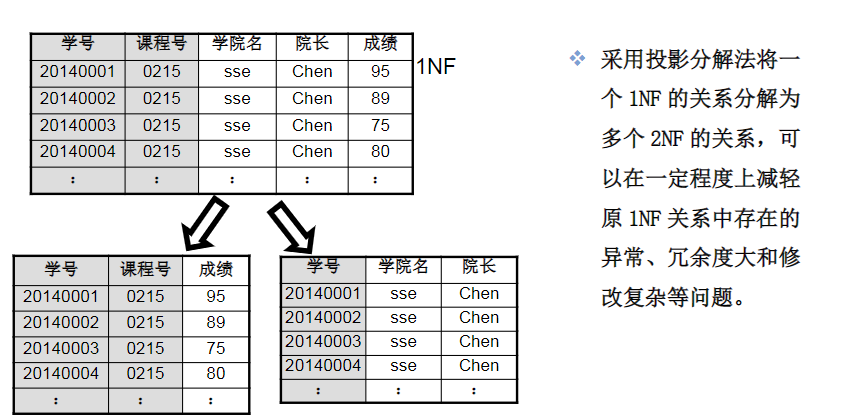
3NF


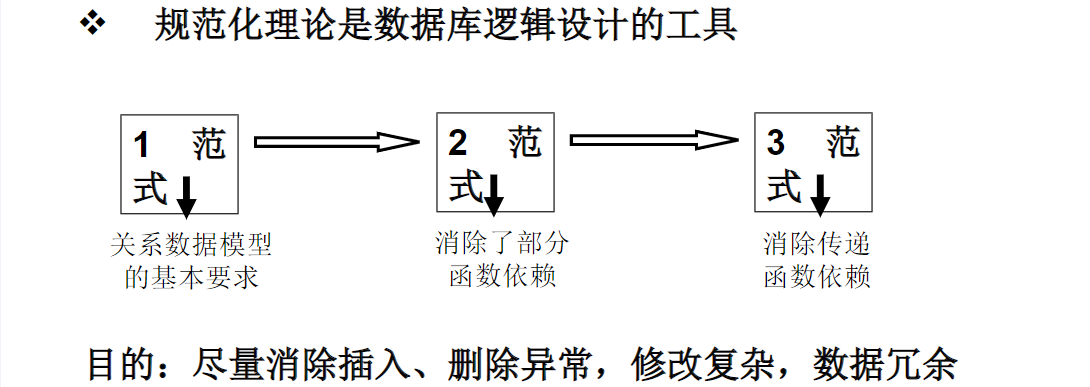
BCNF





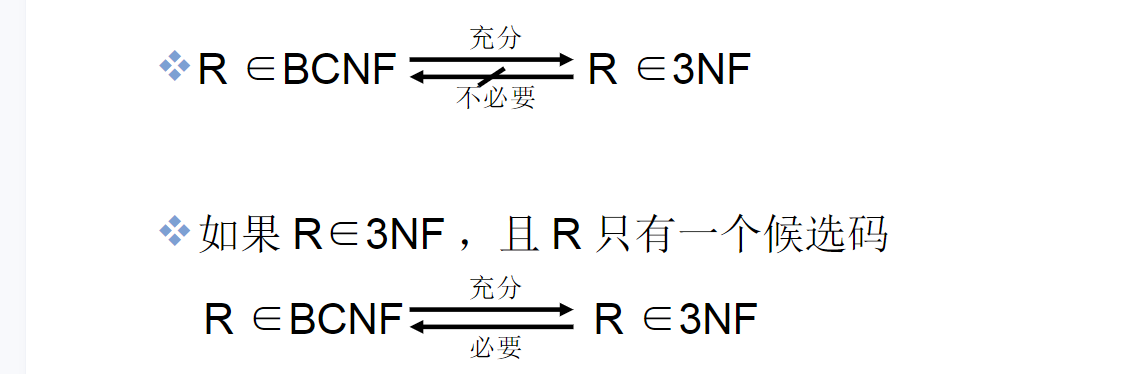
多值依赖







4NF



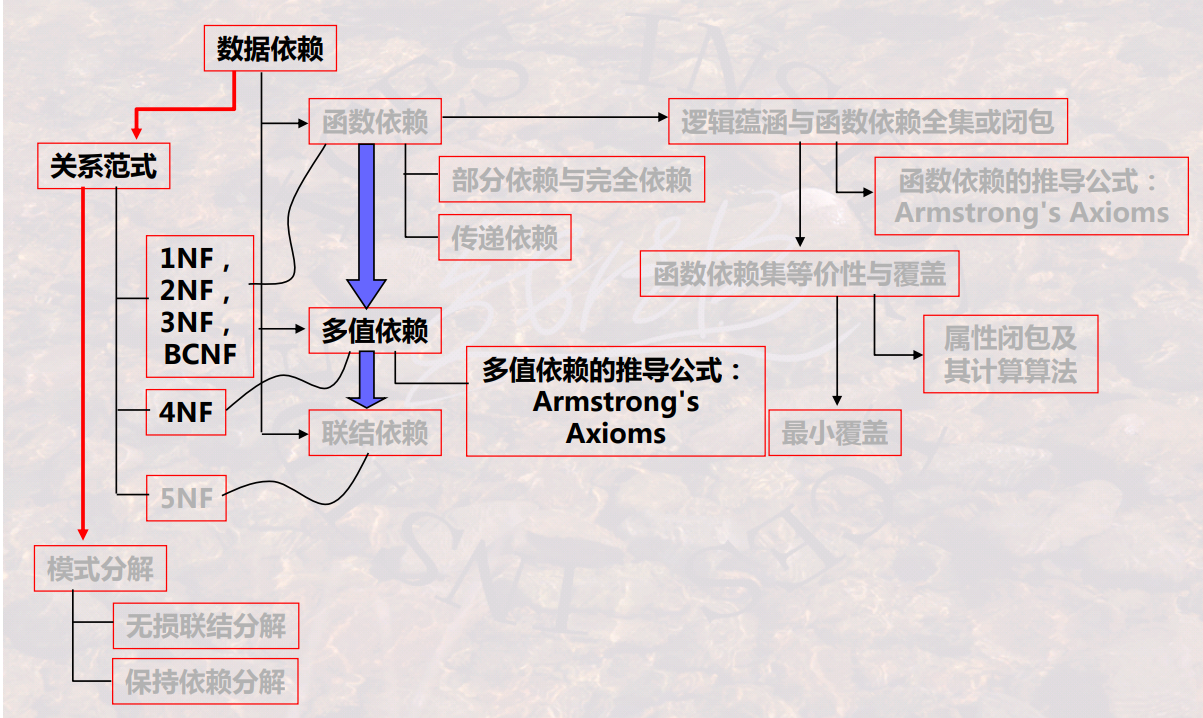
9.2.3数据依赖的公理化系统









9.2.4模式分解

 9.2.4.1无损连接
9.2.4.1无损连接

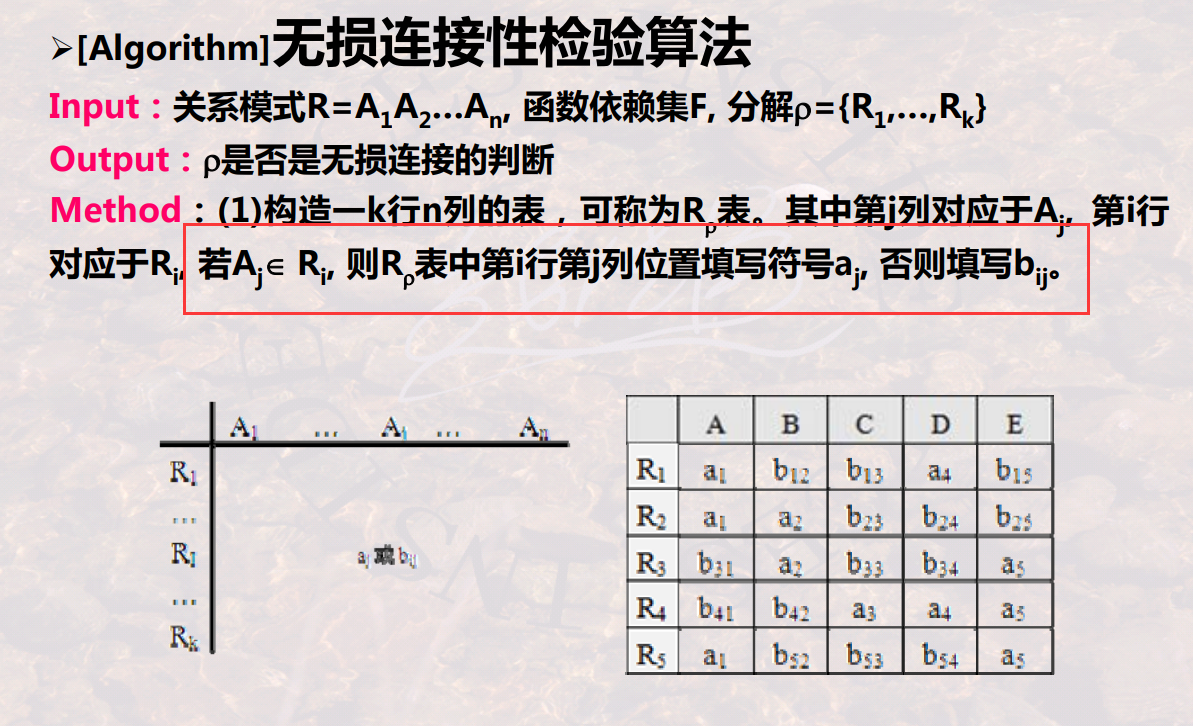
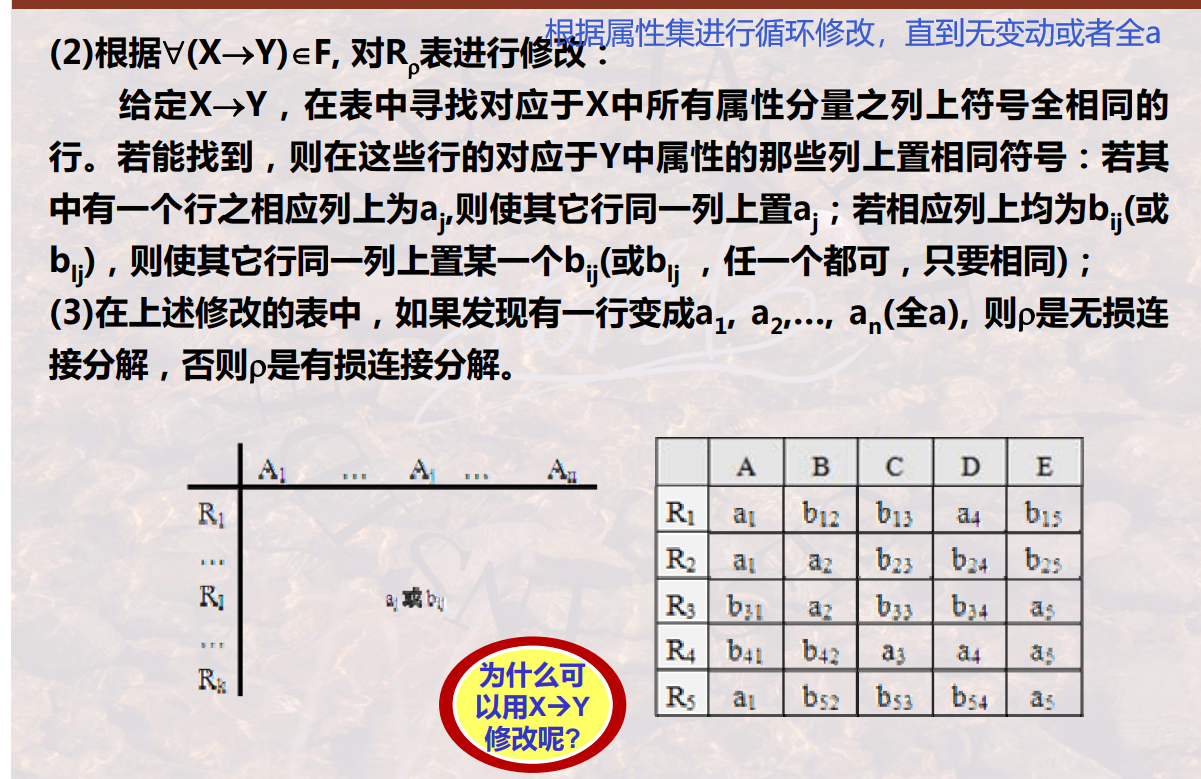

9.2.4.2保持依赖

相关文章:

(九)关系数据理论
函数依赖:设R(U)是属性集U上的关系模式。X、Y是属性集U的子集。若对于R(U)的任意一个可能的关系r,r中不可能存在两个元组在X上的属性值相等,而在Y上的属性值不等,则称X函数确定Y或Y函数依赖于X,记作X→Y。(即只要X 上的…...

【经验分享】Ubuntu下如何解决问题arm-linux-gcc:未找到命令
【经验分享】Ubuntu下如何解决问题arm-linux-gcc:未找到命令 前言问题分析解决方法 前言 在编译过程中发现一个问题,明明之前安装了gcc-4.6版本,版本信息都是正常显示的,刚安装上去的时候也是可以用的。但不知道什么原因突然不能…...

【算法刷题day10】Leetcode:232.用栈实现队列、225. 用队列实现栈
文章目录 Leetcode 232.用栈实现队列解题思路代码总结 Leetcode 225. 用队列实现栈解题思路代码总结 stack、queue和deque对比 草稿图网站 java的Deque Leetcode 232.用栈实现队列 题目:232.用栈实现队列 解析:代码随想录解析 解题思路 一个栈负责进&a…...

sql注入详解
ps:简单说下这里只写了我能理解的明白的,后面的二阶注入,堆叠注入没写 手工sql注入 1.存在sql注入本质上就是数据库过滤的不严格或者未进行过滤,1 and 11,返回正常,1 and 12 返回不正常,说明带到数据库里面…...

[蓝桥杯 2022 省 B] 李白打酒加强版
题目链接 [蓝桥杯 2022 省 B] 李白打酒加强版 题目描述 话说大诗人李白,一生好饮。幸好他从不开车。 一天,他提着酒壶,从家里出来,酒壶中有酒 2 2 2 斗。他边走边唱: 无事街上走,提壶去打酒。 逢店加一倍…...
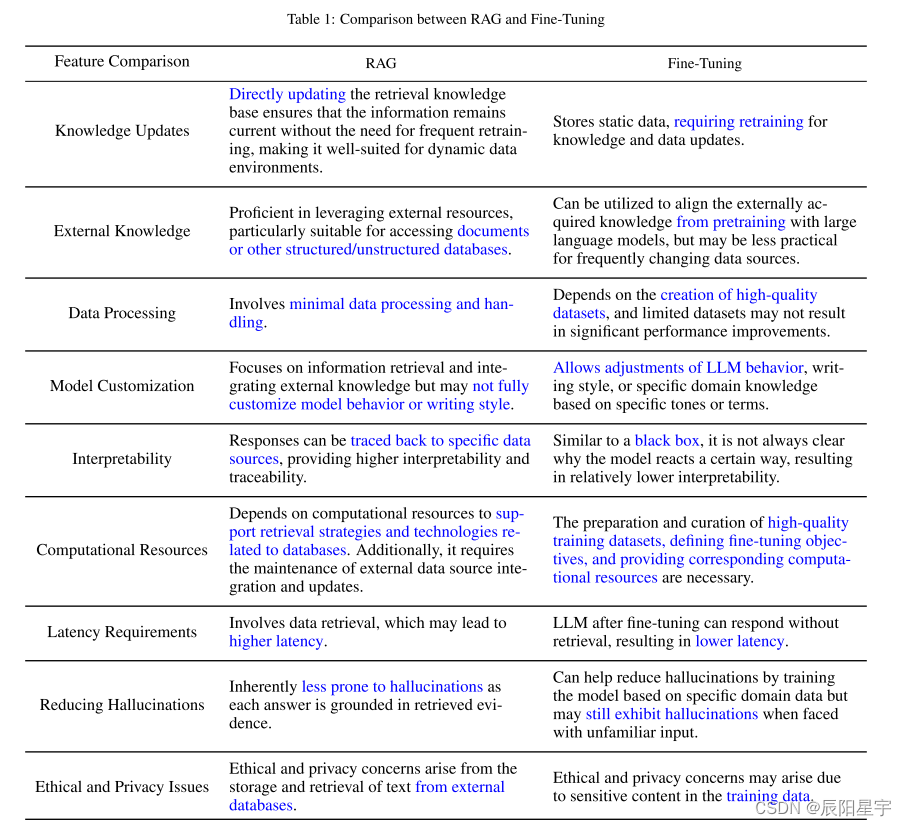
【检索增强】Retrieval-Augmented Generation for Large Language Models:A Survey
本文简介 1、对最先进水平RAG进行了全面和系统的回顾,通过包括朴素RAG、高级RAG和模块化RAG在内的范式描述了它的演变。这篇综述的背景下,更广泛的范围内的法学硕士研究RAG的景观。 2、确定并讨论了RAG过程中不可或缺的核心技术,特别关注“…...
EVM Layer2 主流解决方案
深度解析主流 EVM Layer 2 解决方案:zk Rollups 和 Optimistic Rollups 随着以太坊网络的不断演进和 DeFi 生态系统的迅速增长,以太坊 Layer 2 解决方案日益受到关注。 其中,zk Rollups 和 Optimistic Rollups 作为两种备受瞩目的主流 EVM&…...

go中结构体标签:omitempty、json꞉“name“、 gorm꞉“column꞉name“、yaml꞉“name“
在Go语言中,结构体标签(Struct Tags)提供了一种在编译时附加到结构体字段上的元数据,这些标签可以被运行时的反射(reflection)机制读取。结构体标签的存在意义和用途非常广泛,主要包括ÿ…...

七月论文审稿GPT第4版:通过paper-review数据集微调Mixtral-8x7b,对GPT4胜率超过80%
前言 在此之前,我司论文审稿项目组已经通过我司处理的paper-review数据集,分别微调了RWKV、llama2、gpt3.5 16K、llama2 13b、Mistral 7b instruct、gemma 7b 七月论文审稿GPT第1版:通过3万多篇paper和10多万的review数据微调RWKV七月论文审…...

【QT学习】1.qt初识,创建qt工程,使用按钮,第一个交互按钮
1.初识qt--》qt是个框架,不是语言 1.学习路径 一 QT简介 ,QTCreator ,QT工程 ,QT的第一个程序,类,组件 二 信号与槽 三 对话框 四 QT Desiner 控件 布局 样式 五 事件 六 GUI绘图 七 文件 八 …...

JavaScript_与html结合方式
JavaScript_语法 ECMAScript:客户端脚本语言的标准 1.基本语法 1.1 与html结合方式(2种) 1. 内部JS 定义<script>,标签体内容就是js代码 2. 外部JS 定义<script>,通过src属性引入外部的 js文件 注意: 1.<script>…...

WPF —— 动画
wpf动画类型 1<类型>Animation这些动画称为from/to/by动画或者叫基本动画,他们会在起始值或者结束值进行动画处理,常用的例如 <DoubleAnimation> 2 <类型>AnimationUsingKeyFrames: 关键帧动画,功能要比from/to这些动画功…...

前端二维码生成工具小程序:构建营销神器的技术解析
摘要: 随着数字化营销的不断深入,二维码作为一种快速、便捷的信息传递方式,已经广泛应用于各个领域。本文旨在探讨如何通过前端技术构建一个功能丰富、操作简便的二维码生成工具小程序,为企业和个人提供高效的营销支持。 一、引言…...

光伏发电量预测(Python代码,CNN结合LSTM,TensorFlow框架)
1.数据集(开始位置),数据集免费下载链接:https://download.csdn.net/download/qq_40840797/89051099 数据集一共8列,第一列是时间,特征列一共有6列:"WindSpeed" - 风速 "Sunshi…...

GPT带我学-设计模式11-组合模式
设计模式类型 结构型设计模式 使用场景 将对象组合成树状结构来表现"部分-整体"的层次结构。这种模式能够使得客户端对单个对象和组合对象的使用具有一致性。这句话太抽象了,拿一个实际的网站菜单树例子来说。 例子:网页菜单树 一个网站的…...

Centos7 elasticsearch-7.7.0 集群搭建,启用x-pack验证 Kibana7.4用户管理
前言 Elasticsearch 是一个分布式、RESTful 风格的搜索和数据分析引擎,能够解决不断涌现出的各种用例。 作为 Elastic Stack 的核心,它集中存储您的数据,帮助您发现意料之中以及意料之外的情况。 环境准备 软件 …...

[CSS]中子元素在父元素中居中
元素居中 对于当行文字居中,比较简单,设置text-align:center和text-height为盒子高度即可 对于父元素中子元素居中,要实现的话有以下几个方法 方法1:利用定位margin:auto <style>.father {width: 500px;heig…...

电脑突然死机怎么办?
死机是电脑常见的故障问题,尤其是对于老式电脑来说,一言不合电脑画面就静止了,最后只能强制关机重启。那么你一定想知道是什么原因造成的吧,一般散热不良最容易让电脑死机,还有系统故障,比如不小心误删了系…...

Kyligence 正式加入华为“同舟共济”行动计划,成为行业数智化“联盟级伙伴”
让“生态飞轮”旋转让“生态飞轮”旋转3月14日至15日,华为中国合作伙伴大会 2024 在深圳召开。本次大会以“因聚而生,数智有为”为主题,皆在升级“伙伴华为”数智体系,共筑解决方案竞争力,共赢数智世界新机遇。Kyligen…...

大模型推理框架——text-generation-inference
项目地址:https://github.com/huggingface/text-generation-inference 安装 安装rust curl --proto =https --tlsv1.2 -sSf https://sh.rustup.rs | sh安装 Protoc PROTOC_ZIP=protoc-21.12-linux-x86_64.zip curl -OL https://github.com/protocolbuffers/protobuf/relea…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...
