100种思维模型之混沌与秩序思维模型-027
人类崇尚秩序与连续性,我们习惯于我们的日常世界,它以线性方式运作,没有不连续或突跳。
为此,我们学会了期望各种过程以连续方式运行,我们的内心为了让我们更有安全感,把很多事物的结果归于秩序,可控,看得见的因果。
比如:一个人创业成功,他更容易归于自己的努力,克服痛苦的过程,而很容易忽视,背后的运气,时代的趋势,他人隐藏的帮助等混沌与非连续性的因素。
混沌与秩序思维模型,即一个提醒我们处在一个充满混沌和不连续性的世界,既要看到混沌现象背后的趋势,又要看到秩序状态背后的混沌,继而找到一套与混沌世界共处的思维方式。
01、何谓混沌与秩序思维模型
一、混沌与秩序
所谓混沌,简单的来说就是一个系统的响应对初始状态相当敏感,初始条件的一个微小的变化都可能会导致最终状态的巨大差别。
如,经典案例蝴蝶效应,一只蝴蝶在巴西亚马逊轻拍翅膀,可能导致一个月后德克萨斯州的一场龙卷风。
所谓秩序,指的是有条理、不混乱,意指在自然进程和社会进程中都存在着某种程度的一致性、连续性和确定性。
如,自然秩序中的日出日落,月亏月盈等;社会秩序中的社会进步,社会分裂到统一等。
而所谓混沌与秩序,指的是混沌和秩序的关系,既对立的又是统一的。即那些看似杂乱无章的混沌并不是完全随机的,相反,它却是有迹可循的,有着内在普适的规律。
如,养育孩子,因为孩子是一个生命体,她终将成长成一个什么样的人是一个复杂事件,但是这个复杂事件里面有简单规则,即樊登老师在《陪孩子终身成长》一书中提及的培养孩子的三根支柱:
一是无条件的爱;二是价值感;三是终身成长的心态。
当家长把以上三根支柱给到孩子,孩子他将会为自我负责,自我迭代,向上成长。
二、混沌与秩序思维模型
所谓混沌与秩序思维模型,就是将混沌与秩序思维应用到解决问题上。
生活、工作中在遇到重要问题、重大决策时,运用混沌与秩序思维进行分析,即看到事物的复杂混沌,又能看到复杂混沌背后的秩序。
即以开放的心态拥抱生活中的不确定性,继而不断提升认知助力找到混沌事件的关键秩序,执行有效干预,最后有效的解决问题。
02、混沌与秩序思维模型生活中的运用
一、养护绿植
“家里养盆绿植太难了,市场上买一盆绿植,在家养不到2个月就给养死,然后继续买,继续死……”
养盆绿植真的那么难?
是的,挺难的!养盆绿植是一个混沌事件,同时亦是一个有秩序事件!
为什么说养盆绿植是一个混沌事件呢?
因为植物有其自身的生长规律,同时亦受周边环境,如温度、光照、养分、水分等影响。
所以,室内绿植养护一般需要做到以下几个方面:
1.选择合适的室内绿植;一般选择耐阴,喜凉爽环境的植物,如绿萝、吊篮、发财树、君子兰等。
2.养护具体操作;如适时的浇水、施肥、松土、换盆、修建等。
以上,如果某一个方面做不好都会影响植物的成活及长势。
那么为什么又说养盆植物是一个有秩序事件呢?
一般朋友把绿植养死的原因无外乎以下两种:一种是经常浇水,活活把绿植给淹死的;一种是买回家就不管,活活给干死的。
室内绿植养护的关键操作是:掌握好浇水方法——“见干见湿、不干不浇、浇必浇透”。
所谓“见干见湿、不干不浇、浇必浇透”指的是,室内栽种植物无需经常浇水,亦不可零浇水,要做到适时浇水,即要等花盆中的土干透了在浇水,且每次浇水一定要浇透,同样下一次浇水也是等土干透了再浇,且做到浇透水,如此反复即可。
二、养育孩子
养育孩子的道理跟养护植物相似,亦是一个混沌事件,且混沌中有秩序。
养育孩子是一个混沌事件!
即非简单干预就可以产生一个好的结果,如有些家长认为孩子有多动症,不能静下来好好写作业,于是家长就决定盯着孩子写作业,希望这样做能帮孩子养成一个良好的学习习惯。
然事情总是不如愿,这个良好的学习习惯迟迟未到来,还落了一个坏习惯——写作业不能不盯着,如果有一次不盯着就不写或者不好好写。
为什么会这样?
这是因为,家长盯着写作业的行为让孩子慢慢地意识到,我是一个需要被盯的人,没有人盯我,我写不了作业。且自我找不到学习本身的乐趣,学习是家长要求的,不是基于自身热爱学习而去主动学习,学习主动性丢失。
养育孩子亦是一个有秩序事件,即混沌背后有其秩序!
即《陪养孩子终身成长》一书中,樊登老师总结的养育孩子的三根支柱:
一是无条件的爱;二是价值感;三是终身成长的心态。
无条件的爱,让孩子获得满满的学习、成长的动力;价值感,让孩子感受到与他人、与世界的关系,给他人、世界创造价值;终身成长的心态,让孩子拥抱生活中的不确定性,以学习、成长的心态面对生活中的困难,以致不畏困难,勇于面对困难,继而获得不断地成长。
三、自我成长
所谓成长,俞敏洪老师曾说:成长就是让自己的内在和外在的价值都得到提升。
而所谓内在的价值提升指的是让自己变得积累更多的聪明、才智、才华和才能,外在价值的提升就是别人看你的时候觉得你这个人会越来越值钱或者越来越值得尊敬。
看到以上这个定义,我们可知成长是一个混沌事件,但是这个混沌的背后有其秩序。
成长背后的秩序是什么呢?
用老喻的人生算法来说,即把自己打造成一辆赛车(清楚的知道自己的目标),四个轮子“感知、认知、决策、行动”(好奇感知、灰度认知、黑白决策、疯子行动),通过刻意练习,自我迭代,训练、管理这辆车,最后获得不断成长。
03、怎么更好的应用
怎么拥有混沌与秩序思维呢?
以下3点建议可能对我们有帮助:
一是立刻行动,快速试错;
对于混沌事件,有时候我们很难找到规律,或者根本看不到规律。
这时不如找到一个口子先切入,先干起来,即立即行动,快速试错。
如,实际生活中确定自己的兴趣,依据社会认知生涯理论模型:
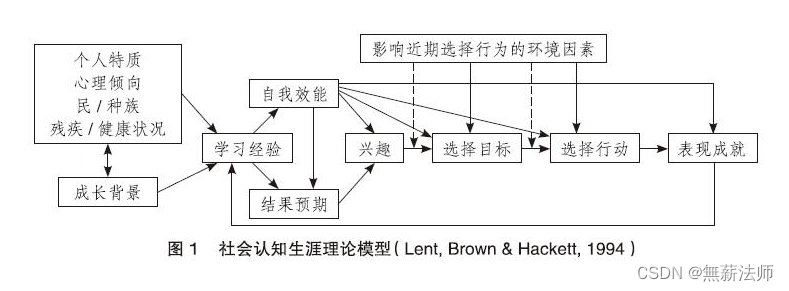
绘制兴趣并非天生的,而是后天习得!
一件事,做着做着,突然自我感觉良好,感觉自己可以胜任,且最后通过行动确实做成了,如此不断强调,最后这件事情就成了自己的兴趣。
日本天才画家佐伯佑三,他为了寻找到属于自己的独特风格,从不蜷缩在自己狭小的世界,不断尝试,拿出勇气,不断否定,寻找,再否定,再寻找。
他认为:不害怕外界的刺激,不躲在自己狭小的世界里,而是勇敢的去尝试,才能找到自己真正想要的和擅长的。不甘于现状,才能蜕变重生。
二是获得反馈,不断迭代;
依据《游戏改变世界》一书可知,我们人类需要反馈,且要反馈及时。
所以,我们要及时给自己反馈,通过反馈告诉自己哪些做的很好,接下来继续坚持;哪些需要做一些改进,接下来要迭代完善;哪些做的不好,接下来就给予淘汰。
而对于混沌中的秩序,我们通过反馈,查看是否找到了混沌背后的秩序,如果没有找到,继续找,且不断的迭代完善。
三是冗余备份策略;
混沌事件是复杂的,往往容易受环境影响,当环境变化时,针对原来秩序的方案、策略也许就不能用了,所以,我们要考虑环境变化时候的备选方案,多备份,继而获得反脆弱性。
04、写在最后
人“天生”崇尚秩序与连续性,畏惧混乱和非连续性!
所以我们每个人,每一秒都在混沌中寻找秩序。
混沌,是因为人很无知~~~秩序,是因为人在认知~~~
相关文章:

100种思维模型之混沌与秩序思维模型-027
人类崇尚秩序与连续性,我们习惯于我们的日常世界,它以线性方式运作,没有不连续或突跳。 为此,我们学会了期望各种过程以连续方式运行,我们的内心为了让我们更有安全感,把很多事物的结果归于秩序,…...
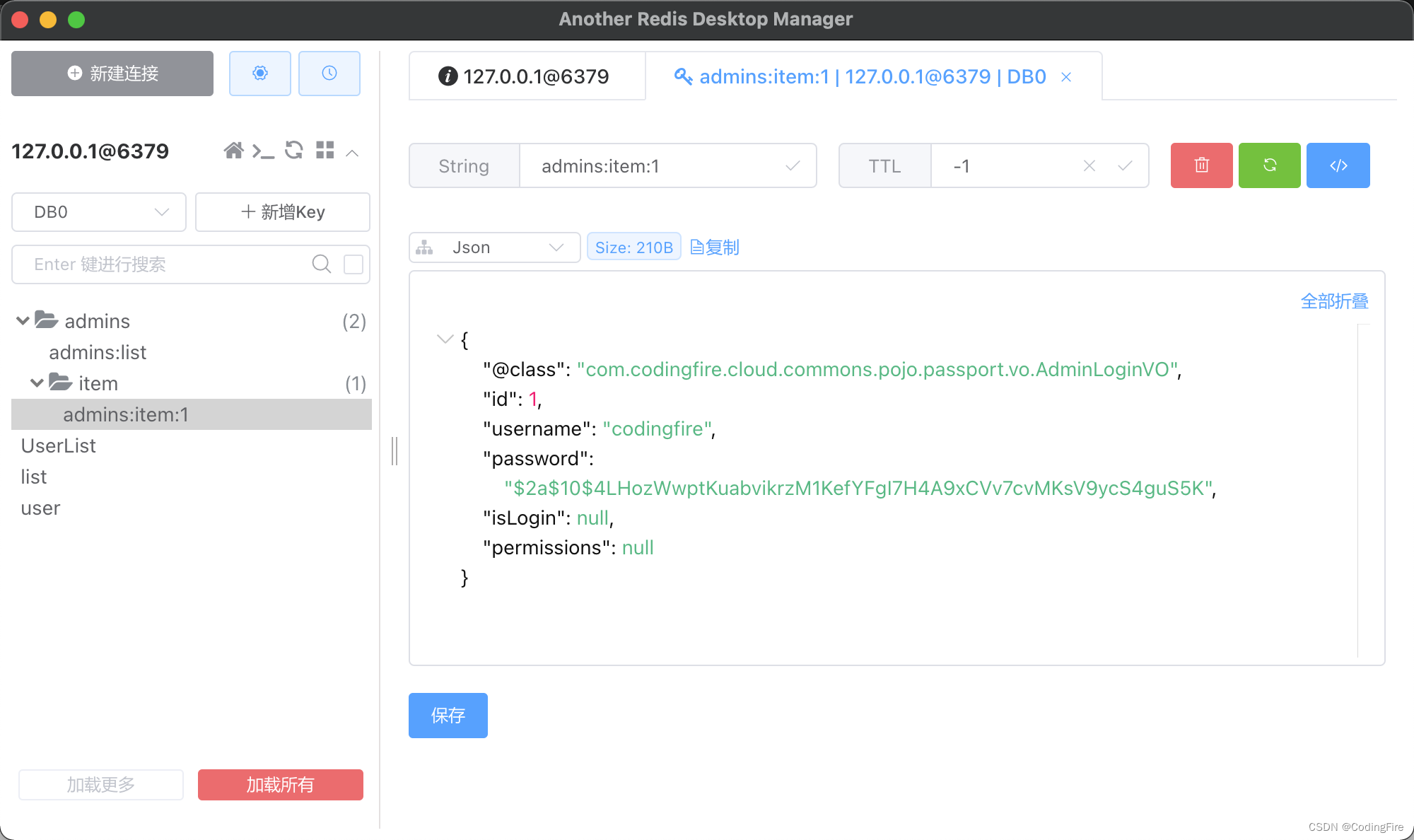
Java开发 - Redis初体验
前言 es我们已经在前文中有所了解,和es有相似功能的是Redis,他们都不是纯粹的数据库。两者使用场景也是存在一定的差异的,本文目的并不重点说明他们之间的差异,但会简要说明,重点还是在对Redis的了解和学习上。学完本…...

Python - 使用 pymysql 操作 MySQL 详解
目录创建连接 pymsql.connect() 方法的可传参数连接对象 conn pymsql.connect() 方法游标对象 cursor() 方法使用示例创建数据库表插入数据操作数据查询操作数据更新操作数据删除操作SQL中使用变量封装使用简单使用: import pymysqldb pymysql.connect(host,user…...
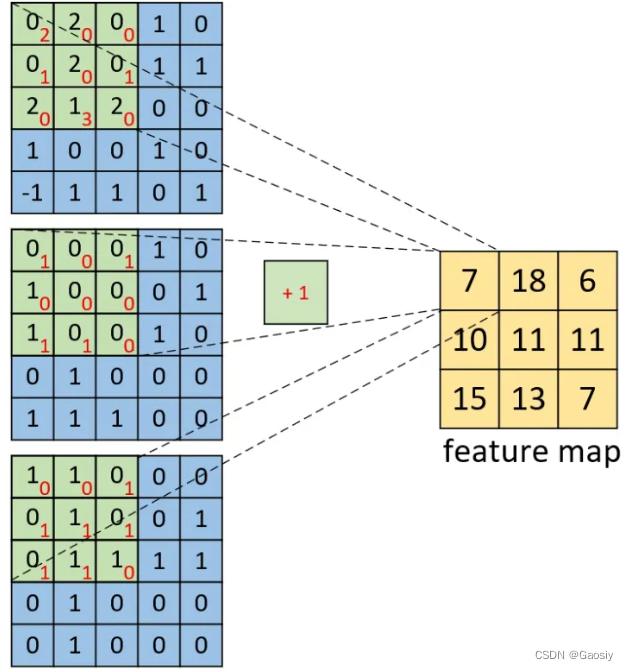
机器学习-卷积神经网络CNN中的单通道和多通道图片差异
背景 最近在使用CNN的场景中,既有单通道的图片输入需求,也有多通道的图片输入需求,因此又整理回顾了一下单通道或者多通道卷积的差别,这里记录一下探索过程。 结论 直接给出结论,单通道图片和多通道图片在经历了第一…...
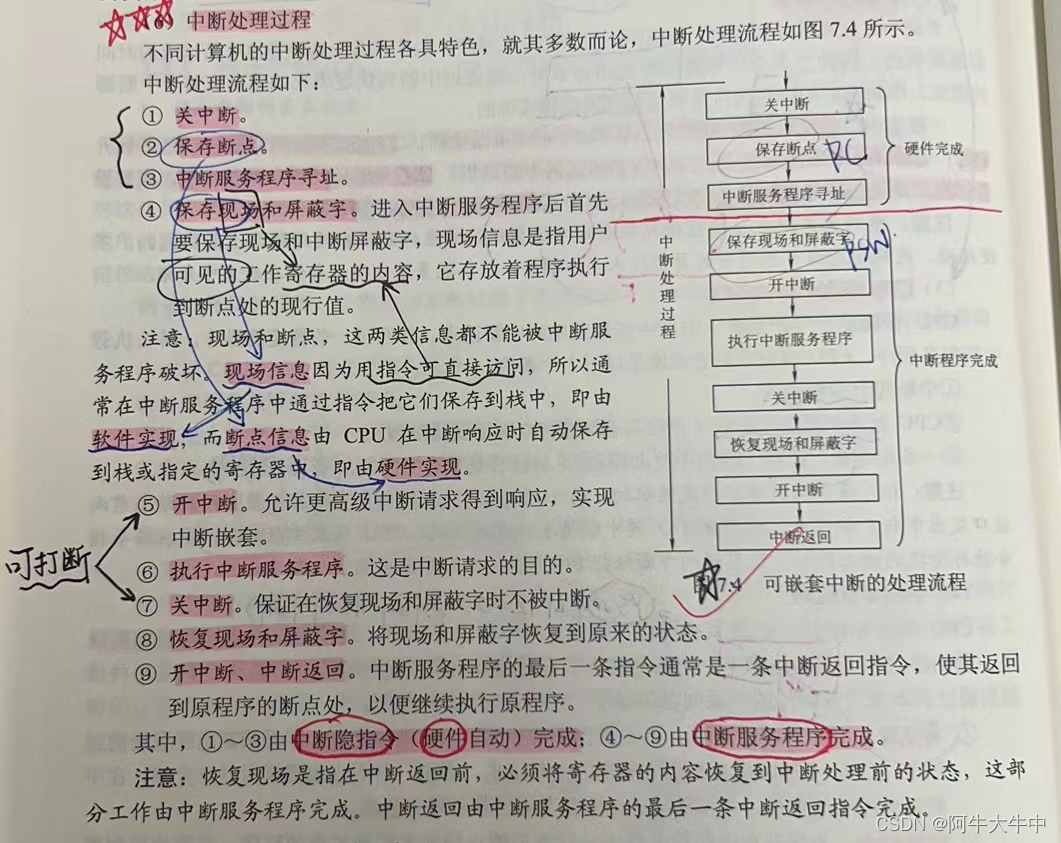
考研复试——计算机组成原理
文章目录计算机组成原理1. 计算机系统由哪两部分组成?计算机系统性能取决于什么?2. 冯诺依曼机的主要特点?3. 主存储器由什么组成,各部分有什么作用?4. 什么是存储单元、存储字、存储字长、存储体?5. 计算机…...

硬件设计 之摄像头分类(IR摄像头、mono摄像头、RGB摄像头、RGB-D摄像头、鱼眼摄像头)
总结一下在机器人上常用的几种摄像头,最近在组装机器人时,傻傻分不清摄像头的种类。由于本人知识有限,以下资料都是在网上搜索而来,按照摄像头的分类整理一下,供大家参考: 1.IR摄像头: IRinfr…...
)
PTA:C课程设计(2)
山东大学(威海)2022级大一下C习题集(2)2-5-1 字符定位函数(程序填空题)2-5-2 判断回文(程序填空题)2-6-1 数字金字塔(函数)2-6-2 使用函数求最大公约数(函数)2-6-3 使用函数求余弦函…...
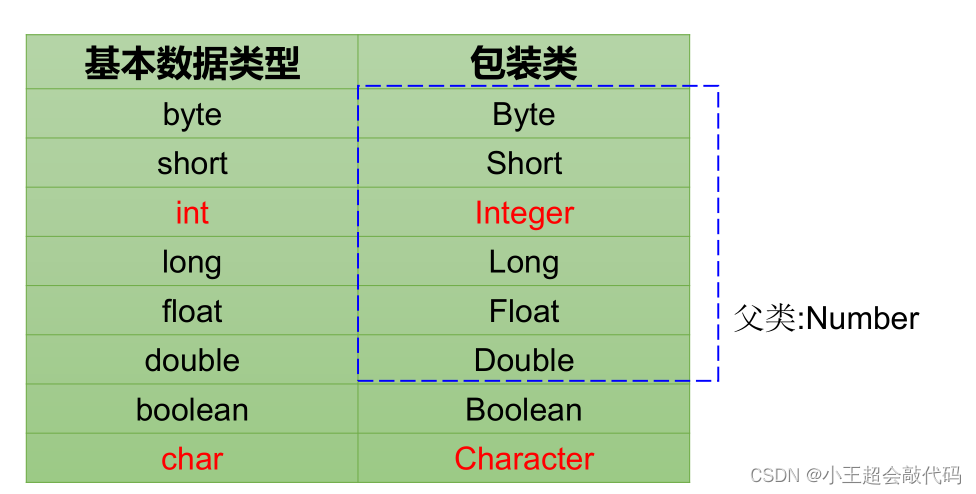
第四章:面向对象编程
第四章:面向对象编程 4.1:面向过程与面向对象 面向过程(POP)与面向对象(OOP) 二者都是一种思想,面向对象是相对于面向过程而言的。面向过程,强调的是功能行为,以函数为最小单位,考虑怎么做。面向对象&…...

Linux 安装npm yarn pnpm 命令
下载安装包 node 下载地址解压压缩包 tar -Jxf node-v19.7.0-linux-x64.tar.xz -C /root/app echo "export PATH$PATH:/app/node-v16.9.0-linux-x64" >> /etc/profile source /etc/profile ln -sf /app/node-v16.9.0-linux-x64/bin/npm /usr/local/bin/ ln -…...
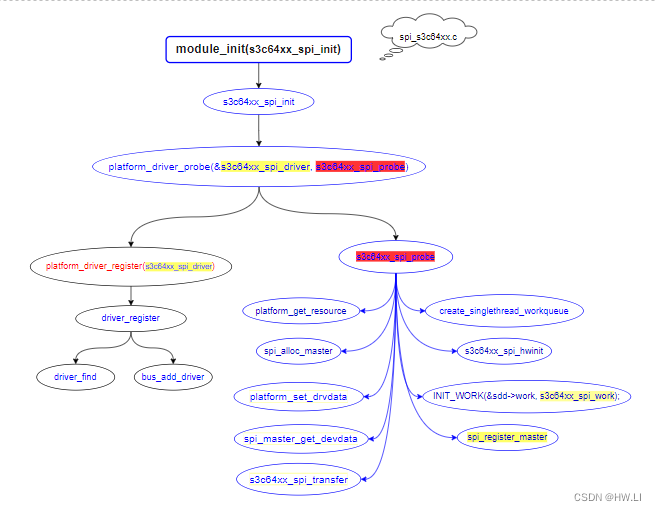
linux SPI驱动代码追踪
一、Linux SPI 框架概述 linux系统下的spi驱动程序从逻辑上可以分为3个部分: SPI Core:SPI Core 是 Linux 内核用来维护和管理 spi 的核心部分,SPI Core 提供操作接口,允许一个 spi master,spi driver 和 spi device 在 SPI Cor…...

Ls-dyna材料的相关学习笔记
Elastic Linear elastic materials -Isotropic:各向同性材料 -orthotropic 正交各向异性的 -anistropic 各向异性的...
)
Arrays方法(copyOfRange,fill)
Arrays方法 1、Arrays.copyOfRange Arrays.copyOfRange的使用方法 功能: 将数组拷贝至另外一个数组 参数: original:第一个参数为要拷贝的数组对象 from:第二个参数为拷贝的开始位置(包含) to:…...
)
AcWing - 蓝桥杯集训每日一题(DAY 1——DAY 5)
文章目录一、AcWing 3956. 截断数组(中等)1. 实现思路2. 实现代码二、AcWing 3729. 改变数组元素(中等)1. 实现思路2. 实现代码三、AcWing 1460. 我在哪?(简单)1. 实现思路2. 实现代码四、AcWin…...
)
RHCSA-文件的其他命令(3.7)
目录 文件的其他命令: 文本内容统计wc 移动和复制(cp) 移动 查找文件的路径 压缩和解压缩 .tar(归档命令) shell-命令解释器 linux中的特殊字符 查看系统上的别名:alias 历史命令(his…...

多线程update导致的mysql死锁问题处理方法
最近想起之前处理过的一个mysql 死锁问题,是在高并发下update批量更新导致的,这里探讨一下发生的原因,以及解决办法; 发生死锁的sql语句如下,其中where条件后的字段是有复合索引的。 update t_push_message_device_h…...
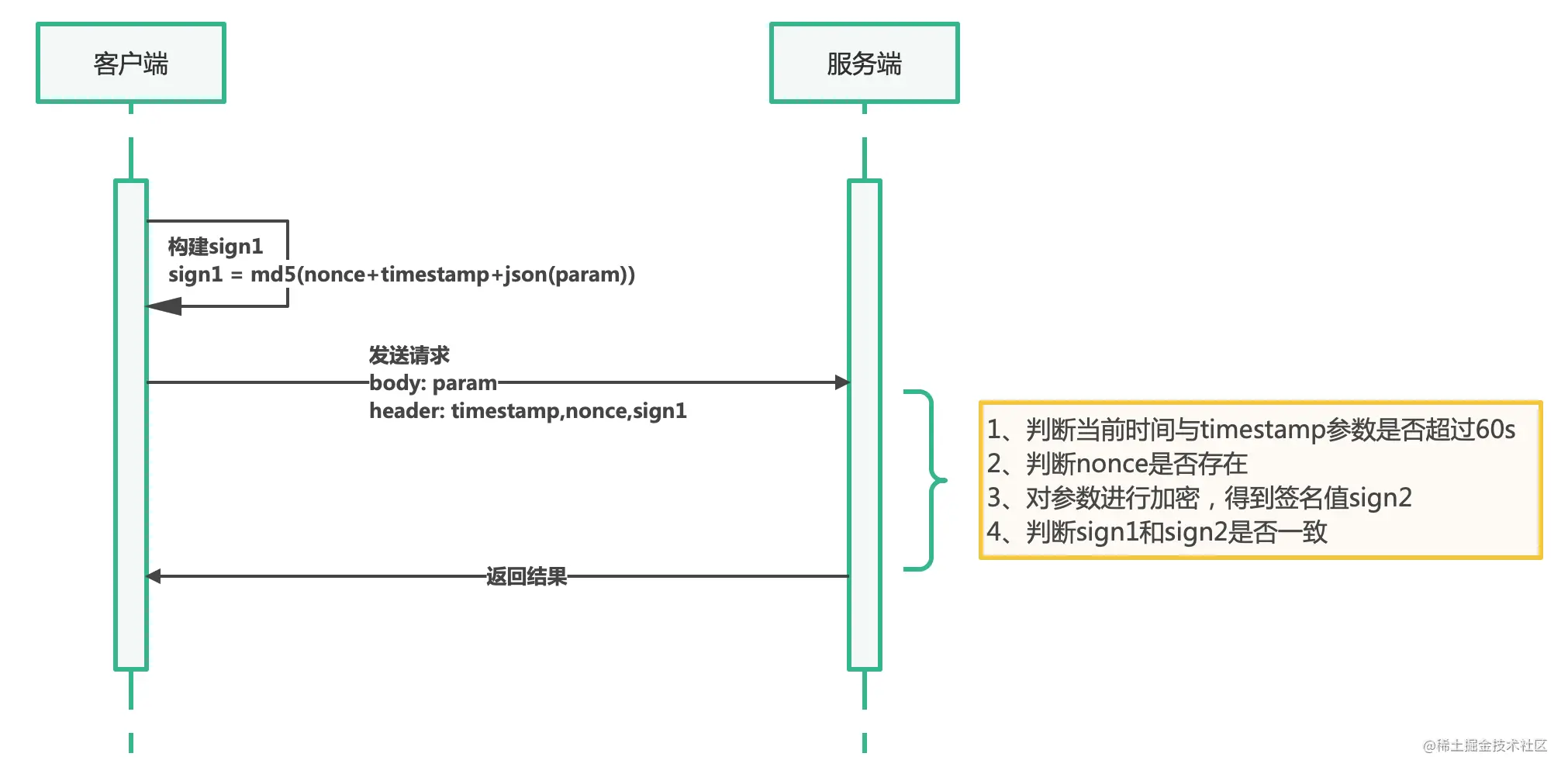
SpringBoot 如何保证接口安全?
为什么要保证接口安全对于互联网来说,只要你系统的接口暴露在外网,就避免不了接口安全问题。 如果你的接口在外网裸奔,只要让黑客知道接口的地址和参数就可以调用,那简直就是灾难。举个例子:你的网站用户注册的时候&am…...

英伟达驱动爆雷?CPU占用率过高怎么办?
又有一新驱动导致CPU占用率过高? 上周英伟达发布531.18显卡驱动,为大家带来了视频超分辨率技术,并为新发布的热门游戏《原子之心》提供支持。 但在安装新驱动后没过不久就有玩家反映,在游戏结束后会出现CPU占用率突然飙升到10%以…...
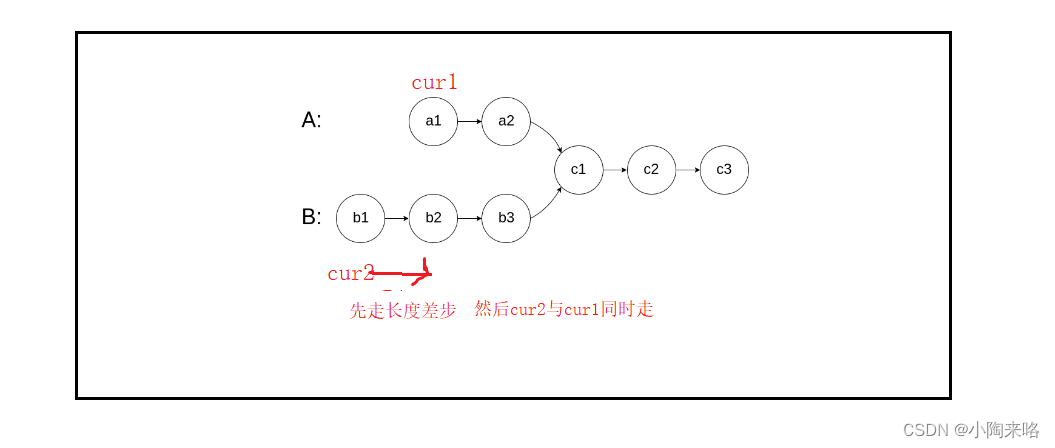
链表经典面试题【典中典】
💯💯💯链表经典面试题❗❗❗炒鸡经典,本篇带有图文解析,建议动手刷几遍。🟥1.反转链表🟧2.合并两个有序链表🟨3.链表分割🟩4.链表的回文结构🟦5.相交链表&…...

Java泛型深入
一. 泛型的概述和优势 泛型概述 泛型:是JDK5中引入的特性,可以在编译阶段约束操作的数据类型,并进行检查。泛型的格式:<数据类型>,注意:泛型只能支持引用数据类型。集合体系的全部接口和实现类都是…...
体验Linux USB 驱动
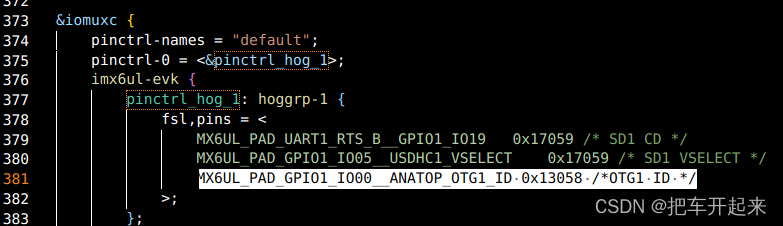
目录 一、USB OTG 二、I.MX6ULL USB 接口简介 硬件原理图 1、USB HUB 原理图 2 、USB OTG 原理图 三、使能驱动 1、打开 HID 驱动 2、 使能 USB 键盘和鼠标驱动 3 、使能 Linux 内核中的 SCSI 协议 4、使能 U 盘驱动 四、测试u盘 五、 Linux 内核自带 USB OTG USB 是…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步:前置条件,启用 OLE 自动化方式 1:使用 SQL 实现启用 OLE 自动化方式 2:Sql Server 2005启动OLE自动化方式 3:Sql Server 2008启动OLE自动化第 2 步:创建存储过程第 3 步:创建触发器扩展 - 如何调试?第 1 步:登录 SQL Server 2008第 2 步…...
