动态规划—机器人移动问题(Java)
😀前言
机器人移动问题是一个经典的动态规划应用场景,它涉及到在给定范围内的位置上进行移动,并计算到达目标位置的方法数。本文将介绍三种解决这一问题的方法:暴力递归、缓存法和动态规划。通过比较不同方法的优缺点,我们将深入理解动态规划在解决问题中的重要性以及如何优化算法以提高性能和空间利用率。
🏠个人主页:尘觉主页
文章目录
- 动态规划--机器人移动问题(Java)
- 机器人移动问题
- 暴力递归
- 缓存法
- 动态规划
- 😄总结
动态规划–机器人移动问题(Java)
机器人移动问题
机器人可在1-N的位置上进行移动,规定三个数据 分别是机器人当前位置 机器人可以移动的步数 机器人的目标位置 计算出机器人用光步数后到达目标位置的方法数
暴力递归
机器人在1-N的范围上进行移动,一共会有3种情况,
在1时,只能右移动
在N时,只能左移动
在中间时,既可以左移,又可以右移;
所以可以根据这几种情况进行暴力递归
递归的终止条件是 当前步数为0 且处于目标位置上
public int moveTimes(int N,int cur,int target,int steps ){//三个参数分别是可以移动的范围 当前位置 目标位置if(steps==0){//如果没有步数了进行返回return cur == target?1:0;}if(cur==1){return moveTimes(N,cur+1,target,steps-1);}if (cur == N){return moveTimes(N,cur-1,target,steps-1);}return moveTimes(N,cur+1,target,steps-1) + moveTimes(N,cur-1,target,steps-1);}
缓存法
通过这种方式我们就可以取得最终的全部可能的情况,但是显然,我们的暴力递归,会多做很对运算。比如当机器人处于中间位置的时,当前的状态是 cur = 5,steps = 10 那么在接下来的递归中我们会有这样的2个分支
(4,9)-> (5,8)/ (3,8) | (6,9)-> (5,8)/(7,8)
那么我们的(5,8)在计算过一次之后,还会再次进行计算。这样的情况下,我们的运行时间就会变得过长 。
所以我们引出了傻缓存法,缓存的作用在于,我们进行一次递归的过程中,便将这一次递归的结果记录到缓存中,当下一次再次递归时,可以直接调用之前在缓存中数,进行返回,而不是继续向下递归了,这种方法就是再用时间来换空间!
那么回到这道题,我们的cache就可以用一个二维数组来进行存储,row为我们的当前位置 col 为我们的可移动步数
//傻缓存法public int moveTimes(int N,int cur,int target,int steps,int[][] cache){//cache需要初始化;所有值换成-1;if(cache[cur][steps]!=-1){return cache[cur][steps];}int result = -1;//分3种情况进行递归移动//basecaseif (steps == 0){result = cur == target?1:0;} else if (cur == 1){result = moveTimes(N,cur+1,target,steps-1,cache);} else if(cur == N){result = moveTimes(N,cur-1,target,steps-1,cache);} else{result = moveTimes(N,cur+1,target,steps-1,cache)+moveTimes(N,cur-1,target,steps-1,cache);}cache[cur][steps] = result;return result;}public void setCache(int[][] cache){for (int i = 0; i < cache.length; i++) {for (int j = 0; j < cache[1].length; j++) {cache[i][j] = -1;}}}
这里相比第一种方式会更快一些,但是也是浪费了较大的空间;
动态规划
我们结合一二一起看,会发现我们能basecase的情况发生时,可以在缓存即二维数组中确定一些数,当 step = 0时,在二维数组中这一列,我们除了是目标位置会返回 1 以外,其他位置都会返回 0 。所以我们就可以把确定的数据填写到二维数组中,在看暴力递归的其他情况,当我们在第 1 行的时候 ,只能向右移动,所以我们的返回值,要从相对于二维数组中的当前位置的左下角中的这个元素获取返回值,同理当我们在最后 1 行的时候,那么就应该从当前位置的左上角进行取返回值了,当我们在中间位置的时候,我们的则是需要从左上和左下相加来获取返回值,依次类推,我们会回到我们最开始的位置,这时就是我们需要的结果了。
public int moveTimes1(int N,int cur,int target,int steps){int[][] cache = new int[N+1][steps+1];//给第一列进行赋值cache[target][0] = 1;for (int i = 1; i <= steps; i++) {//第一行手动操作cache[1][i] = cache[2][i-1];for (int j = 2; j <= N-1 ; j++) {cache[j][i] = cache[j+1][i-1]+cache[j-1][i-1];}cache[N][i] = cache[N-1][i-1];}return cache[cur][steps];}
完整的代码
@SuppressWarnings({"all"})
public class Robot {//测试public static void main(String[] args) {Robot robot = new Robot();int[][] cache = new int[6][6];robot.setCache(cache);System.out.println(robot.moveTimes(5, 2, 3, 5, cache));System.out.println(robot.moveTimes(5,2,3,5));System.out.println(robot.moveTimes1(5,2,3,5));}//动态规划法public int moveTimes1(int N,int cur,int target,int steps){int[][] cache = new int[N+1][steps+1];//给第一列进行赋值cache[target][0] = 1;for (int i = 1; i <= steps; i++) {//第一行手动操作cache[1][i] = cache[2][i-1];for (int j = 2; j <= N-1 ; j++) {cache[j][i] = cache[j+1][i-1]+cache[j-1][i-1];}cache[N][i] = cache[N-1][i-1];}return cache[cur][steps];}//暴力递归法public int moveTimes(int N,int cur,int target,int steps ){//三个参数分别是可以移动的范围 当前位置 目标位置if(steps==0){//如果没有步数了进行返回return cur == target?1:0;}if(cur==1){return moveTimes(N,cur+1,target,steps-1);}if (cur == N){return moveTimes(N,cur-1,target,steps-1);}return moveTimes(N,cur+1,target,steps-1) + moveTimes(N,cur-1,target,steps-1);}//傻缓存法public int moveTimes(int N,int cur,int target,int steps,int[][] cache){//cache需要初始化;所有值换成-1;if(cache[cur][steps]!=-1){return cache[cur][steps];}int result = -1;//分3种情况进行递归移动//basecaseif (steps == 0){result = cur == target?1:0;} else if (cur == 1){result = moveTimes(N,cur+1,target,steps-1,cache);} else if(cur == N){result = moveTimes(N,cur-1,target,steps-1,cache);} else{result = moveTimes(N,cur+1,target,steps-1,cache)+moveTimes(N,cur-1,target,steps-1,cache);}cache[cur][steps] = result;return result;}public void setCache(int[][] cache){for (int i = 0; i < cache.length; i++) {for (int j = 0; j < cache[1].length; j++) {cache[i][j] = -1;}}}
}
😄总结
通过本文的学习,我们了解了三种解决机器人移动问题的方法:暴力递归、缓存法和动态规划。暴力递归虽然简单易懂,但效率低下;缓存法通过牺牲空间来换取时间,提高了效率;而动态规划则利用填充二维数组的方式,避免了重复计算,进一步优化了性能和空间利用率。动态规划在解决各种问题中都有广泛的应用,是一种重要的算法思想。
😁热门专栏推荐
想学习vue的可以看看这个
java基础合集
数据库合集
redis合集
nginx合集
linux合集
手写机制
微服务组件
spring_尘觉
springMVC
mybits
等等等还有许多优秀的合集在主页等着大家的光顾感谢大家的支持
🤔欢迎大家加入我的社区 尘觉社区
文章到这里就结束了,如果有什么疑问的地方请指出,诸佬们一起来评论区一起讨论😁
希望能和诸佬们一起努力,今后我们一起观看感谢您的阅读🍻
如果帮助到您不妨3连支持一下,创造不易您们的支持是我的动力🤞
相关文章:
)
动态规划—机器人移动问题(Java)
😀前言 机器人移动问题是一个经典的动态规划应用场景,它涉及到在给定范围内的位置上进行移动,并计算到达目标位置的方法数。本文将介绍三种解决这一问题的方法:暴力递归、缓存法和动态规划。通过比较不同方法的优缺点,…...

第十一届蓝桥杯物联网试题(省赛)
对于通信方面,还是终端A、B都保持接收状态,当要发送的数组不为空再发送数据,发送完后立即清除,接收数据的数组不为空则处理,处理完后立即清除,分工明确 继电器不亮一般可能是电压不够 将数据加空格再加\r…...

【Python基础教程】5. 数
🎈个人主页:豌豆射手^ 🎉欢迎 👍点赞✍评论⭐收藏 🤗收录专栏:python基础教程 🤝希望本文对您有所裨益,如有不足之处,欢迎在评论区提出指正,让我们共同学习、…...
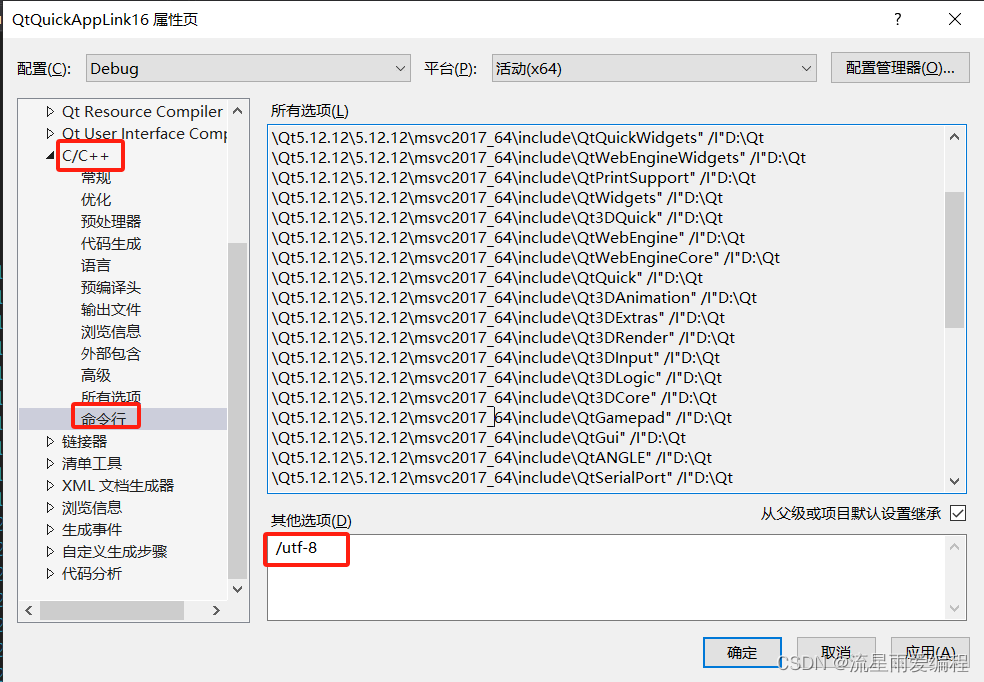
Qt中出现中文乱码的原因以及解决方法
Qt专栏:http://t.csdnimg.cn/C2SDN 目录 1.引言 2.原因分析 3.源文件的编码格式修改方法 4.程序内部使用的默认编码格式修改方法 5.QString转std::string的方法 6.总结 1.引言 在编写Qt程序的时候,或多或少都可能遇到用QString时候,明明…...

Linux 文件相关命令
一、查看文件命令 1)浏览文件less 默认查看文件的前 10 行。 less /etc/services ##功能说明: #1.默认打开首屏内容 #2.按【回车】按行访问 #3.按【空格】按屏访问 #4.【从上向下】搜索用/111,搜索包含111的内容,此时按n继续向下搜&#x…...

K8S Deployment 简介, 1个简单的Kubernetes Deployment YAML 文件
当谈到 Kubernetes 集群中的应用程序部署和管理时,Deployment、ReplicaSet 和 Pod 是三个重要的概念。它们之间存在一定的关系和层次结构。下面是对 Deployment、ReplicaSet 和 Pod 的详细解释以及它们之间的关系。 Deployment(部署) Deploy…...
win11安装WSL UbuntuTLS
win11安装WSL WSL 简介WSL 1 VS WSL 2先决要求安装方法一键安装通过「控制面板」安装 WSL 基本命令Linux发行版安装Ubuntu初始化相关设置root用户密码网络工具安装安装1panel面板指导 WSl可视化工具问题总结WSL更新命令错误Ubuntu 启动初始化错误未解决问题 WSL 简介 Windows …...

第十题:金币
题目描述 国王将金币作为工资,发放给忠诚的骑士。第一天,骑士收到一枚金币;之后两天(第二天和第三天),每天收到两枚金币;之后三天(第四、五、六天),每天收到…...

Windows 11 中Docker的安装教程
选择正确的Docker版本 在Windows上,你可以安装两种类型的Docker:Docker Desktop和Docker Toolbox。Docker Desktop是针对Windows 10 Pro、Enterprise和Education版本的,这些版本内置了Hyper-V虚拟化支持。对于旧版本的Windows,比…...
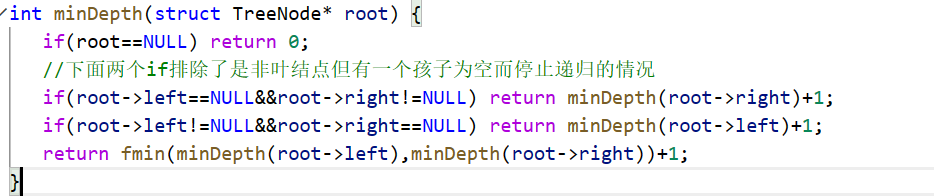
纯C代码模板
一、快排 void QuickSort(int *a,int left,int right){if(left>right) return;else{int low left,high right;int pivot a[low];while(low<high){while(a[high] > pivot && low < high){high--;}a[low] a[high]; //必须先动a[low]while(a[low] < …...
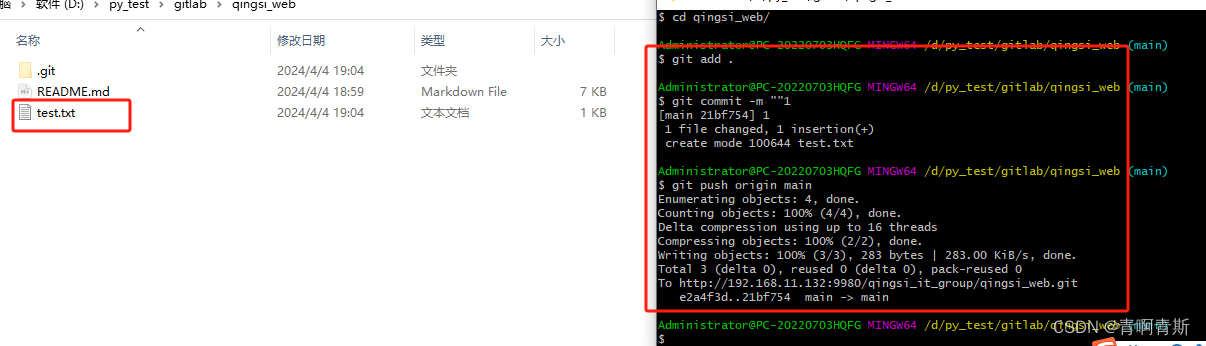
二、GitLab相关操作
GitLab相关操作 一、组、用户、项目管理1.创建组2.创建项目3.创建用户并分配组3.1 创建用户3.2 设置密码3.3 给用户分配组 二、拉取/推送代码1.配置ssh(第一次需要)1.1 创建一个空文件夹1.2 配置本地仓账号和邮箱1.3 生成ssh公钥密钥1.4 gitlab配置公钥 2.拉取代码3.推送代码3.…...

【详细注释+流程讲解】基于深度学习的文本分类 TextCNN
前言 这篇文章用于记录阿里天池 NLP 入门赛,详细讲解了整个数据处理流程,以及如何从零构建一个模型,适合新手入门。 赛题以新闻数据为赛题数据,数据集报名后可见并可下载。赛题数据为新闻文本,并按照字符级别进行匿名…...

Day.21
interface MyInterface{public final static int PI 3;void show();public default void printX(){System.out.println("接口默认方法");}public static void printY(){System.out.println("接口静态方法");}}class MyClass implements MyInterface{publi…...

Spring-IoC 基于注解
基于xml方法见:http://t.csdnimg.cn/dir8j 注解是代码中的一种特殊标记,可以在编译、类加载和运行时被读取,执行相应的处理,简化 Spring的 XML配置。 格式:注解(属性1"属性值1",...) 可以加在类上…...
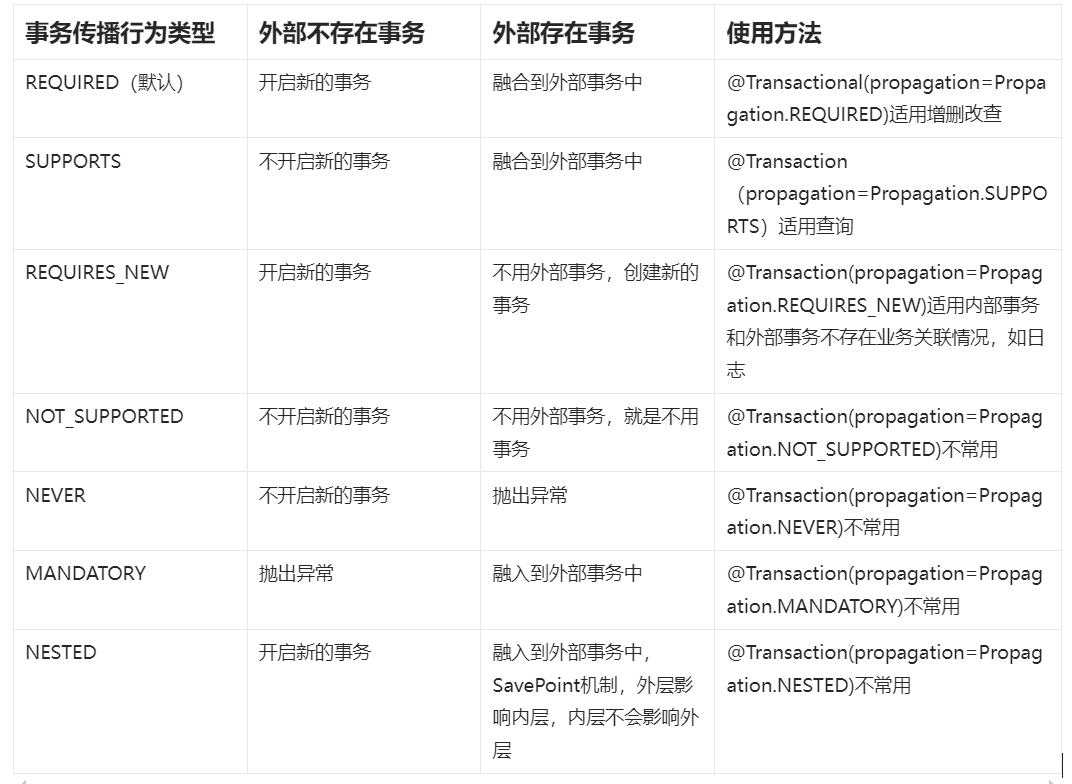
Spring声明式事务以及事务传播行为
Spring声明式事务以及事务传播行为 Spring声明式事务1.编程式事务2.使用AOP改造编程式事务3.Spring声明式事务 事务传播行为 如果对数据库事务不太熟悉,可以阅读上一篇博客简单回顾一下:MySQL事务以及并发访问隔离级别 Spring声明式事务 事务一般添加到…...

【C语言数据库】Sqlite3基础介绍
1. SQLite简介 SQLite is a C-language library that implements a small, fast, self-contained, high-reliability, full-featured, SQL database engine. SQLite is the most used database engine in the world. SQLite is built into all mobile phones and most computer…...
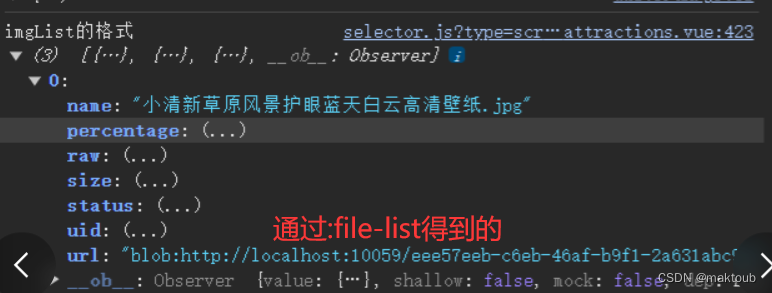
el-upload上传图片图片、el-load默认图片重新上传、el-upload初始化图片、el-upload编辑时回显图片
问题 我用el-upload上传图片,再上一篇文章已经解决了,el-upload上传图片给SpringBoot后端,但是又发现了新的问题,果然bug是一个个的冒出来的。新的问题是el-upload编辑时回显图片的保存。 问题描述:回显图片需要将默认的 file-lis…...
【拓扑空间】示例及详解1
例1 度量空间的任意两球形邻域的交集是若干球形邻域的并集 Proof: 任取空间的两个球形邻域、,令 任取,令 球形领域 例2 规定X的子集族,证明是X上的一个拓扑 Proof: 1. 2., (若干个球形邻域的并集都是的元素,元素…...

linux安装jdk8
上传到某个目录,例如:/usr/local/ tar -xvf jdk-8u144-linux-x64.tar.gz配置环境变量: export JAVA_HOME/usr/local/java export PATH$PATH:$JAVA_HOME/bin设置环境变量: source /etc/profile...
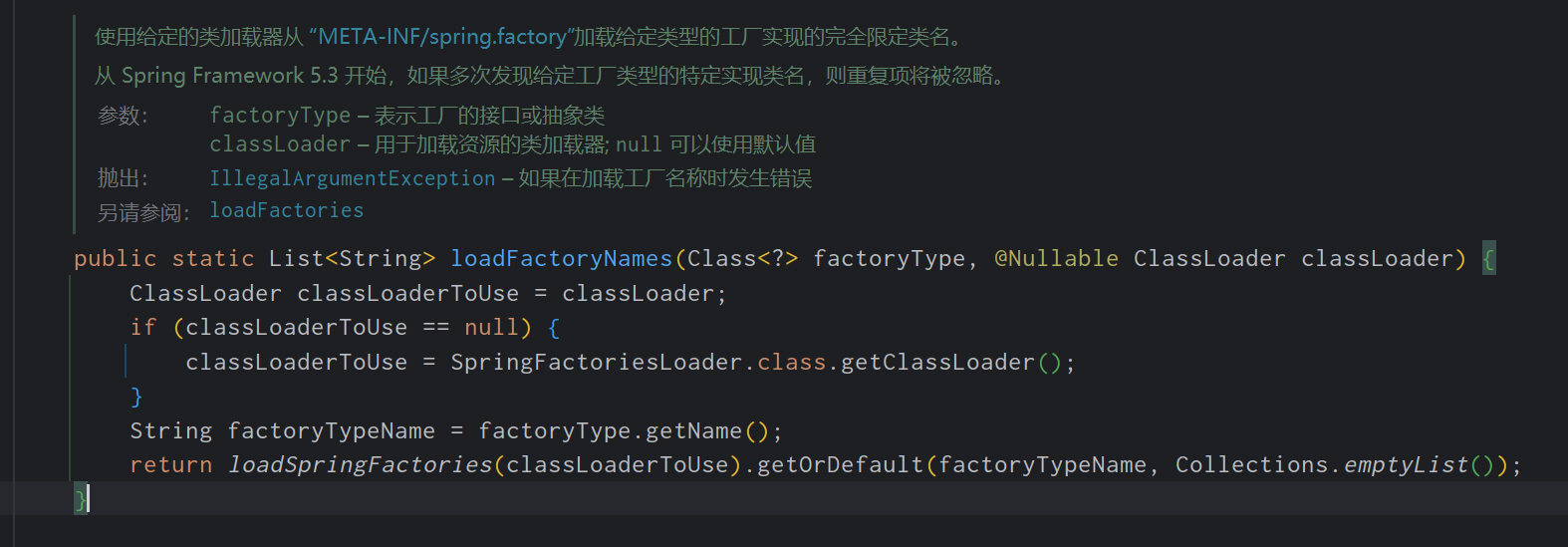
Spring重点知识(个人整理笔记)
目录 1. 为什么要使用 spring? 2. 解释一下什么是 Aop? 3. AOP有哪些实现方式? 4. Spring AOP的实现原理 5. JDK动态代理和CGLIB动态代理的区别? 6. 解释一下什么是 ioc? 7. spring 有哪些主要模块?…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...
