滑动窗口(尺取法/Python)
滑动窗口(尺取法)
算法含义:
在解决关于区间特性的题目时保存搜索区间左右端点,然后根据实际要求不断更新左右端点位置的算法
时间复杂度: O ( n ) O(n) O(n)
空间复杂度: O ( 1 ) O(1) O(1)
在历年真题中,滑动窗口主要有求追偿不重复子串和模拟优先队列求区间最值两个作用
一、求最长不重复字串
不重复子串:字符串的字串中不包含重复字符的字串
from collections import defaultdicts = input()
n = len(s)
# 建立一个字典存储各个元素在窗口中出现的次数
d = defaultdict(int)
ans = 0
# 确定窗口左端
left = 0
for right in range(n):# 如果发现窗口中已经有s[right],将left右移直到窗口中不存在s[right]while d[s[right]] > 0:# 更新字典d[s[left]] -= 1left += 1ans = max(ans, right-left+1)print(ans)
二、模拟优先队列求区间最值
滑动窗口研究区间的性质,可以用于模拟优先队列从而高效求出区间内的最大值和最小值
例题 1: 附近最小(蓝桥杯第14届省模拟赛)
问题描述:
小蓝有一个序列 a [ 1 ] , a [ 2 ] , . . . , a [ n ] a[1],a[2],...,a[n] a[1],a[2],...,a[n]。给定一个正整数 k,请问对于每一个 1 到 n 之间的正整数i, a [ i − k ] , a [ i − k + 1 ] , . . . , a [ i + k ] a[i−k],a[i−k+1],...,a[i+k] a[i−k],a[i−k+1],...,a[i+k] 这 2k+1 个数中的最小值是多少?
当某个下标超过 1 到 n 的范围时,数不存在,求最小值时只取存在的那些值。
输入格式:
输入的第一行包含一整数 n,第二行包含 n 个整数,分别表示 a [ 1 ] , a [ 2 ] , . . . , a [ n ] a[1],a[2],...,a[n] a[1],a[2],...,a[n]。第三行包含一个整数 k
输出格式
输出一行,包含 n 个整数,分别表示对于每个序号求得的最小值。
代码示例:
# 滑动窗口 + 优先队列
n = int(input())
a = [int(i) for i in input().split()]
k = int(input())
# 在数组右边补k个一定不是最小值的数以免分类讨论
a = a + [a[n-1]+1]*k
d = k*2+1 # 窗口宽度
ans = []
q = [] # 递增的优先队列
# 注意i是滑动窗口的右端点
for i in range(n+k):# 如果队列不为空,将所有大于当前元素的队尾元素出队while q and a[q[-1]] > a[i]:q.pop()# 将新元素的下标入队q.append(i)# 检查队头元素是否在新区间范围内if i - q[0] > d-1:q.pop(0)# 将队头元素记录下来if i >= k:ans.append(a[q[0]])# print answer
print(' '.join(list(map(str, ans))))
例题 2: 子矩阵(蓝桥杯第14届省赛真题)
问题描述:
给定一个n x m(n行m列)的矩阵。设一个矩阵的价值为其所有数中的最大值和最小值的乘积。求给定矩阵的所有大小为 a x b (a行b列)的子矩阵的价值的和。答案可能很大,你只需要输出答案对 998244353 取模后的结果。
输入格式:
输入的第一行包含四个整数分别表示n,m,a,b,相邻整数之间使用一个空格分隔。接下来
n行每行包含m个整数,相邻整数之间使用一个空格分隔,表示矩阵中的每个数 A i j A_{ij} Aij。
输出格式
输出一行包含一个整数表示答案。
# 利用滑动窗口模拟优先队列,从而将搜索每一个区间中最值的时间复杂度从O(n*n)优化为O(n)
MOD = 998244353
def get_max(nums,step):# the variable called step store the size of intervalq = []max_list = []for i in range(len(nums)):while q and nums[q[-1]] < nums[i]:# when the end element of prior-quee is small than the new element# pop out the end elementq.pop(-1)# the list store the index of every number because it is more convenient to find # out whether the index is out of the interval or not q.append(i)# when the first element is out of the range of interval, pop it outif q[0] <= i-step:q.pop(0)# when the queue has been built, add the first element into the answer listif i >= step-1:max_list.append(nums[q[0]])return max_list
# using the same theory,we can find out the minist number
def get_min(nums,step):q = []min_list = []for i in range(len(nums)):while q and nums[q[-1]] > nums[i]:q.pop(-1)q.append(i)if q[0] <= i-step:q.pop(0)if i >= step-1:min_list.append(nums[q[0]])return min_list
# similarly,we can calculate out the sum of all the numbers in the interval
def get_sum(nums,step):sum_list = []temp = 0# the pointer called i is actually the right pointer# the left pointer's value is i-step+1for i in range(len(nums)):if i < step - 1:temp += nums[i]elif i == step-1:temp += nums[i]sum_list.append(temp)else:temp -= nums[i-step]temp += nums[i]sum_list.append(temp)return sum_list# the main part of the algorithm
# firstly,use the function to find out all the line's extremum
n,m,a,b = map(int,input().split())
matrix = []
for i in range(n):matrix.append([int(j) for j in input().split()])
# zip the row
m_max_one = []
m_min_one = []
for i in range(n):m_max_one.append(get_max(matrix[i], b))m_min_one.append(get_min(matrix[i], b))
# transpose the temporary matrix and zip again
# the result is the collection of extremum matrix
m_max_two = [[0]*n for i in range(len(m_max_one[0]))]
m_min_two = [[0]*n for i in range(len(m_min_one[0]))]
for i in range(len(m_max_one[0])):for j in range(len(m_max_one)):m_max_two[i][j] = m_max_one[j][i]m_min_two[i][j] = m_min_one[j][i]
# zip the col
m_max = []
m_min = []
for i in range(len(m_max_two)):m_max.append(get_max(m_max_two[i], a))m_min.append(get_min(m_min_two[i], a))
# calculate the sum of all the sub_matrixs' value
res = 0
for i in range(len(m_max)):for j in range(len(m_max[0])):res += m_max[i][j]*m_min[i][j]res %= MOD
print(res)
相关文章:
)
滑动窗口(尺取法/Python)
滑动窗口(尺取法) 算法含义: 在解决关于区间特性的题目时保存搜索区间左右端点,然后根据实际要求不断更新左右端点位置的算法 时间复杂度: O ( n ) O(n) O(n) 空间复杂度: O ( 1 ) O(1) O(1) 在历年真题…...

【打印SQL执行日志】⭐️Mybatis-Plus通过配置在控制台打印执行日志
目录 前言 一、Mybatis-Plus 开启日志的方式 二、测试 三、日志分析 章末 前言 小伙伴们大家好,相信大家平时在处理问题时都有各自的方式,最常用以及最好用的感觉还是断点调试,但是涉及到操作数据库的执行时,默认的话在控制台…...

Vue后台管理系统常用组件的优缺点分析
以下是Vue后台管理系统常用组件的优缺点分析: Element UI 优点: 丰富的组件库:Element UI 提供了大量的组件,包括表单、表格、弹窗、导航等,可以满足各种后台管理系统的需求。易于使用:Element UI 的组件…...
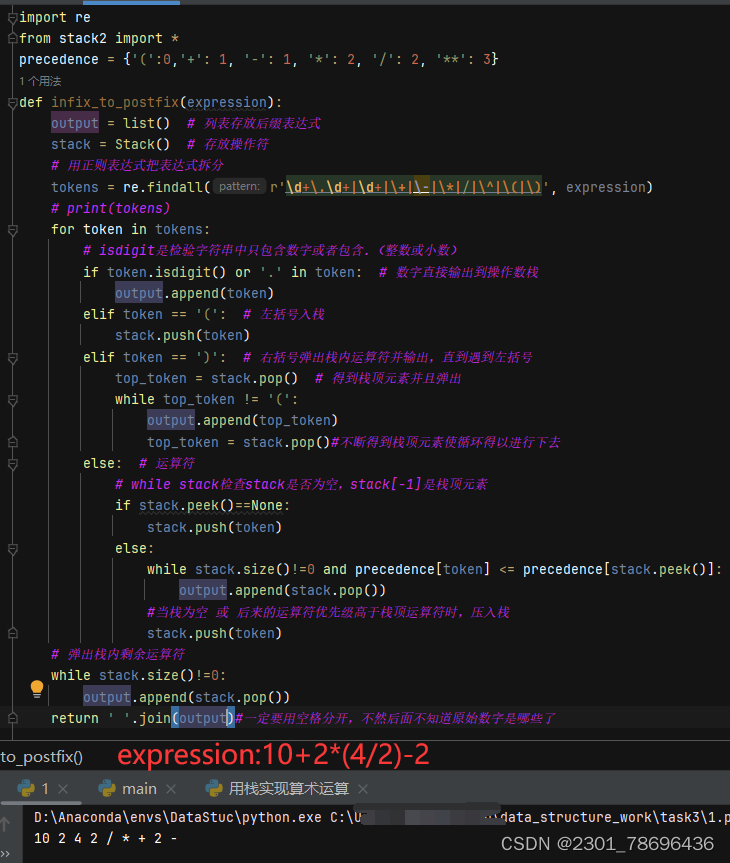
栈的应用——用栈实现算数混合运算表达式的计算
1、单目运算符双目运算符 算数运算符分为单目运算符和双目运算符等 单目运算符只需要一个操作数,双目运算符需要两个操作数 双目运算符最常见:常见的算术运算符:*/,比较运算符:<>=等等以下是一些单目运算符:正号 (+): 用于表示正数或给数值一个正号。例如:+5 仍然…...
)
动态规划—机器人移动问题(Java)
😀前言 机器人移动问题是一个经典的动态规划应用场景,它涉及到在给定范围内的位置上进行移动,并计算到达目标位置的方法数。本文将介绍三种解决这一问题的方法:暴力递归、缓存法和动态规划。通过比较不同方法的优缺点,…...

第十一届蓝桥杯物联网试题(省赛)
对于通信方面,还是终端A、B都保持接收状态,当要发送的数组不为空再发送数据,发送完后立即清除,接收数据的数组不为空则处理,处理完后立即清除,分工明确 继电器不亮一般可能是电压不够 将数据加空格再加\r…...

【Python基础教程】5. 数
🎈个人主页:豌豆射手^ 🎉欢迎 👍点赞✍评论⭐收藏 🤗收录专栏:python基础教程 🤝希望本文对您有所裨益,如有不足之处,欢迎在评论区提出指正,让我们共同学习、…...
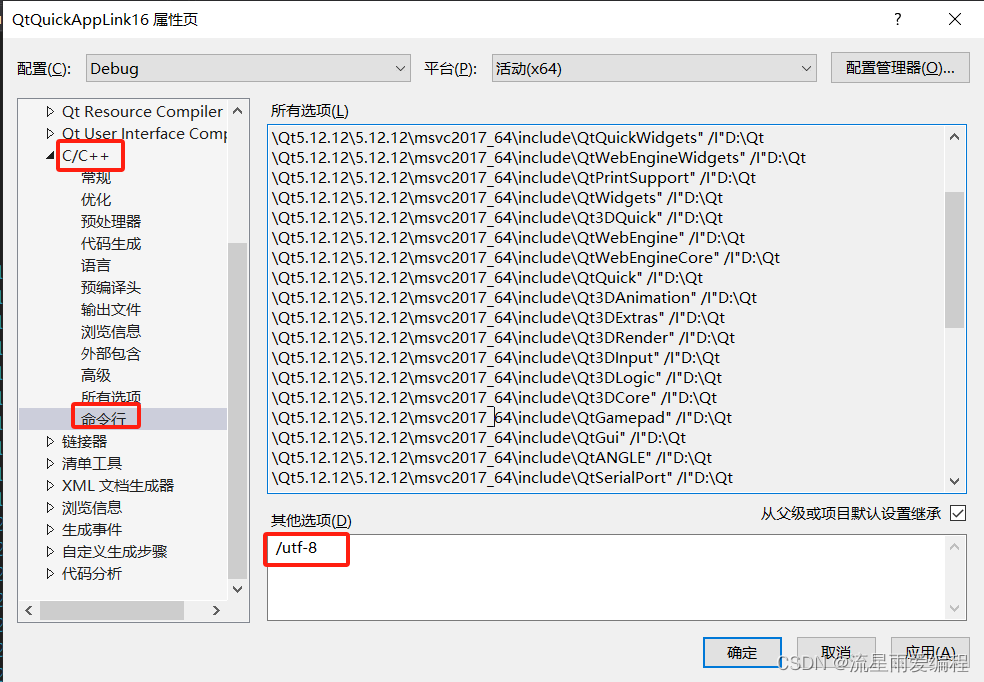
Qt中出现中文乱码的原因以及解决方法
Qt专栏:http://t.csdnimg.cn/C2SDN 目录 1.引言 2.原因分析 3.源文件的编码格式修改方法 4.程序内部使用的默认编码格式修改方法 5.QString转std::string的方法 6.总结 1.引言 在编写Qt程序的时候,或多或少都可能遇到用QString时候,明明…...

Linux 文件相关命令
一、查看文件命令 1)浏览文件less 默认查看文件的前 10 行。 less /etc/services ##功能说明: #1.默认打开首屏内容 #2.按【回车】按行访问 #3.按【空格】按屏访问 #4.【从上向下】搜索用/111,搜索包含111的内容,此时按n继续向下搜&#x…...

K8S Deployment 简介, 1个简单的Kubernetes Deployment YAML 文件
当谈到 Kubernetes 集群中的应用程序部署和管理时,Deployment、ReplicaSet 和 Pod 是三个重要的概念。它们之间存在一定的关系和层次结构。下面是对 Deployment、ReplicaSet 和 Pod 的详细解释以及它们之间的关系。 Deployment(部署) Deploy…...
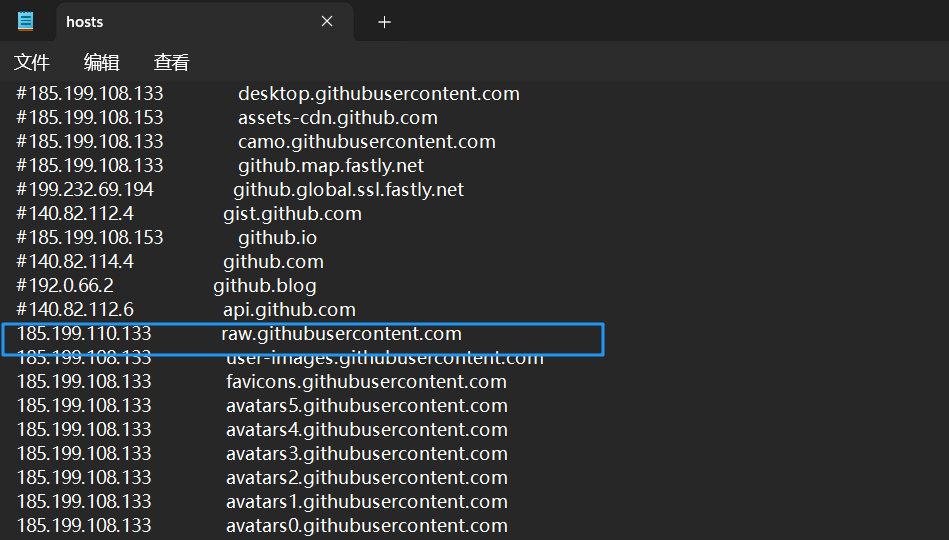
win11安装WSL UbuntuTLS
win11安装WSL WSL 简介WSL 1 VS WSL 2先决要求安装方法一键安装通过「控制面板」安装 WSL 基本命令Linux发行版安装Ubuntu初始化相关设置root用户密码网络工具安装安装1panel面板指导 WSl可视化工具问题总结WSL更新命令错误Ubuntu 启动初始化错误未解决问题 WSL 简介 Windows …...

第十题:金币
题目描述 国王将金币作为工资,发放给忠诚的骑士。第一天,骑士收到一枚金币;之后两天(第二天和第三天),每天收到两枚金币;之后三天(第四、五、六天),每天收到…...

Windows 11 中Docker的安装教程
选择正确的Docker版本 在Windows上,你可以安装两种类型的Docker:Docker Desktop和Docker Toolbox。Docker Desktop是针对Windows 10 Pro、Enterprise和Education版本的,这些版本内置了Hyper-V虚拟化支持。对于旧版本的Windows,比…...
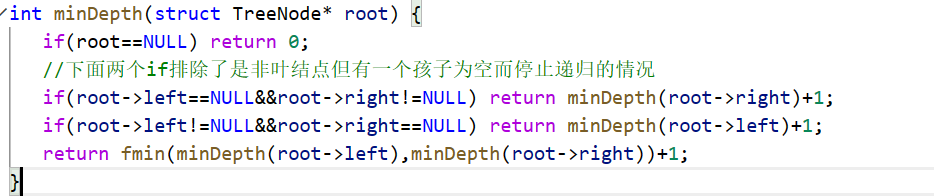
纯C代码模板
一、快排 void QuickSort(int *a,int left,int right){if(left>right) return;else{int low left,high right;int pivot a[low];while(low<high){while(a[high] > pivot && low < high){high--;}a[low] a[high]; //必须先动a[low]while(a[low] < …...
二、GitLab相关操作
GitLab相关操作 一、组、用户、项目管理1.创建组2.创建项目3.创建用户并分配组3.1 创建用户3.2 设置密码3.3 给用户分配组 二、拉取/推送代码1.配置ssh(第一次需要)1.1 创建一个空文件夹1.2 配置本地仓账号和邮箱1.3 生成ssh公钥密钥1.4 gitlab配置公钥 2.拉取代码3.推送代码3.…...

【详细注释+流程讲解】基于深度学习的文本分类 TextCNN
前言 这篇文章用于记录阿里天池 NLP 入门赛,详细讲解了整个数据处理流程,以及如何从零构建一个模型,适合新手入门。 赛题以新闻数据为赛题数据,数据集报名后可见并可下载。赛题数据为新闻文本,并按照字符级别进行匿名…...

Day.21
interface MyInterface{public final static int PI 3;void show();public default void printX(){System.out.println("接口默认方法");}public static void printY(){System.out.println("接口静态方法");}}class MyClass implements MyInterface{publi…...

Spring-IoC 基于注解
基于xml方法见:http://t.csdnimg.cn/dir8j 注解是代码中的一种特殊标记,可以在编译、类加载和运行时被读取,执行相应的处理,简化 Spring的 XML配置。 格式:注解(属性1"属性值1",...) 可以加在类上…...
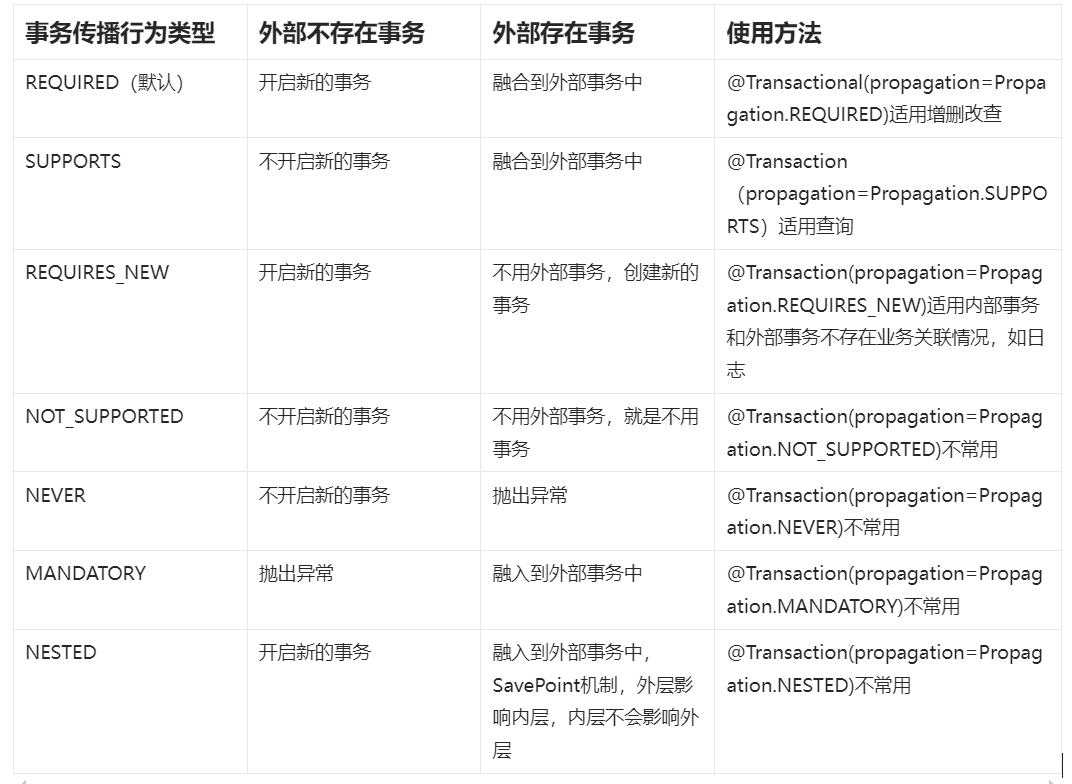
Spring声明式事务以及事务传播行为
Spring声明式事务以及事务传播行为 Spring声明式事务1.编程式事务2.使用AOP改造编程式事务3.Spring声明式事务 事务传播行为 如果对数据库事务不太熟悉,可以阅读上一篇博客简单回顾一下:MySQL事务以及并发访问隔离级别 Spring声明式事务 事务一般添加到…...

【C语言数据库】Sqlite3基础介绍
1. SQLite简介 SQLite is a C-language library that implements a small, fast, self-contained, high-reliability, full-featured, SQL database engine. SQLite is the most used database engine in the world. SQLite is built into all mobile phones and most computer…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...
