ST表(数据结构中的问题)
RMQ问题
RMQ问题指对于数值,每次给一个区间[l,r],要求返回区间区间的最大值或最小值
也就是说,RMQ就是求区间最值的问题
对于RMQ问题,容易想到一种O(n)的方法,就是用i直接遍历[l,r]区间,找出不断比较a[i]与max的大小关系,然后不断更新max,最后得出的就是最大值
但如果要进行多次查询,这个算法就会变得特别慢
于是,我们利用倍增和动态规划的思想,利用‘ST表’这个数据结构来帮助解决。
ST表
ST表是一种“静态求区间最值”的数据结构,本质上是一种dp。
假设我们要求区间的最大值(最小值类似),设状态st[i][j]表示从i开始,大小为2^j的长度的区间的最大值,即区间[i,i+2^j-1]的最大值
状态转移方程st[i][j]=max[st[i][j-1],st[i+(1<<(j-1))] [j-1]]; (1<<(j-1))相当于2^j-1
分成左右两个相等的区间
注意状态转移的方向和保证区间合法
区间查询
为了查询区间[l,r]的最大值,它可以分解为两个小区间的最大值,例如要求[2,7]的最大值,可以分解为[2,2+2*2-1],[7-2*2+1,7]的最大值,也就是(st[2][2],st[7-4][2])
从2开始长度为2的最大值,和从5开始,长度为2的最大值
拓展一下,[l,r]区间,需要找出一个k,使得2^k<=r-l+1,k<=log2(r-l+1),可以分解为max(st[l][k],st[r-2^k+1][k]) 一个是从头开始,一个是从尾开始
int getMax(int l,int r){
return max(str[l][k],st[r-(1<<k)+1][k]);
}
例题
区间最大值
题目描述
给定一个长度为 N 的数组 a,其值分别a1,a2,...,aN。
现有 Q 个询问,每个询问包含一个区间,请回答该区间的最大值为多少。
输入描述
输入第 11 行包含两个正整数 N,Q,分别表示数组 a 的长度和询问的个数。
第 22 行包含 N 个非负整数a1,a2,...,aN,表示数组 a 元素的值。
第 3∼Q+2 行每行表示一个询问,每个询问包含两个整数 L,R,表示区间的左右端点.
输出描述
输出共 Q 行,每行包含一个整数,表示相应询问的答案。
输入输出样例
示例 1
输入
5 5
1 2 3 4 5
1 1
1 2
1 3
3 4
2 5
输出
1
2
3
4
5package ST;
import java.util.*;
public class chapter1 {public static void main(String[] args) {// TODO Auto-generated method stubScanner scan=new Scanner(System.in);int n=scan.nextInt();int q=scan.nextInt();long []a=new long [n];for(int i=0;i<n;i++) {a[i]=scan.nextLong();}int m=(int)Math.ceil(Math.log(n)/Math.log(2));//对m进行向上取整,2^nlong [][] st=new long [n][m];for(int i=0;i<n;i++) {st[i][0]=a[i];}for(int k=1;k<m;k++) {for(int i=0;i+(1<<k)<n;i++) {st[i][k]=Math.max(st[i][k-1],st[i+(1<<(k-1))][k-1]);}}while(q-->0) {int l=scan.nextInt()-1;//数组从0开始所以需要减1int r=scan.nextInt()-1;int len=r-l+1;int k=(int)(Math.log(len)/Math.log(2));int max= (int) Math.max(st[l][k],st[r-(1<<k)+1][k] );System.out.println(max);}}}
相关文章:
)
ST表(数据结构中的问题)
RMQ问题 RMQ问题指对于数值,每次给一个区间[l,r],要求返回区间区间的最大值或最小值 也就是说,RMQ就是求区间最值的问题 对于RMQ问题,容易想到一种O(n)的方法,就是用i直接遍历[l,r]区间&…...

一、OpenCV(C#版本)环境搭建
一、Visual Studio 创建新项目 二、选择Windows窗体应用(.NET Framework) 直接搜索模板:Windows窗体应用(.NET Framework) 记得是C#哈,别整成VB(Visual Basic)了 PS:若搜索搜不到,直接点击安装多个工具和…...

ubuntu远程服务部署,Docker,蓝牙无线局域网,SSH,VNC,xfce4,NextTerminal,宝塔,NPS/NPC,gost,openwrt
SSH服务 apt update apt upgrade -y apt install -y openssh-server/etc/ssh/sshd_config PermitRootLogin yesDocker curl -fsSL https://get.docker.com | bash -s docker --mirror Aliyun apt install -y docker-compose宝塔 wget -O install.sh https://download.bt.cn…...

kettle安装与部署使用教程
kettle 官网下载与部署使用 文章目录 kettle 官网下载与部署使用1. 前言:2. 访问官方网站:3. Download Pentaho3.1 官网首页**滑动到最底**,寻找下载链接:3.2 跳转到下载界面后,选择 Pentaho Community Edition (CE)3.…...

【C语言】编译和链接
1. 翻译环境和运行环境 在ANSI C的任何⼀种实现中,存在两个不同的环境。 第1种是翻译环境,在这个环境中源代码被转换为可执⾏的机器指令(⼆进制指令)。 第2种是执⾏环境,它⽤于实际执⾏代码。 2. 编译环境 那翻译环境…...

Python学习: 错误和异常
Python 语法错误 解析错误(Parsing Error)通常指的是程序无法正确地解析(识别、分析)所给定的代码,通常是由于代码中存在语法错误或者其他无法理解的结构导致的。这可能是由于缺少括号、缩进错误、未关闭的引号或其他括号等问题造成的。 语法错误(Syntax Error)是指程序…...

WebGIS 之 vue3+vite+ceisum
1.项目搭建node版本在16以上 1.1创建项目 npm create vite 项目名 1.2选择框架 vuejavaScript 1.3进入项目安装依赖 cd 项目名 npm install 1.4安装cesium依赖 pnpm i cesium vite-plugin-cesium 1.5修改vite.config.js文件 import { defineConfig } from vite import vue fr…...

## CSDN创作活动:AI技术创业有哪些机会?
AI技术创业有哪些机会? 人工智能(AI)技术作为当今科技创新的前沿领域,为创业者提供了广阔的机会和挑战。随着AI技术的快速发展和应用领域的不断拓展,未来AI技术方面会有哪些创业机会呢? 方向一࿱…...

中医肝胆笔记
目录 肝胆的经络足厥阴肝经足少阳胆经 疏肝健脾的药舒肝益脾颗粒:逍遥丸:疏肝颗粒 -> 疏肝理气的力度大-> 肝郁的程度深,逍遥丸没用的是时候用这个加味逍遥丸 -> 清热的力度最大->适用 肝郁火大,舌苔黄丹栀逍遥丸->…...

理解Go语言中break语句是如何工作的
break语句常用来中断循环。当循环与switch或select一起使用时,开发者经常执行了错误的break语句。 让我们来看下面的示例。我们在for循环里使用了switch,如果循环索引值是2,那么我们想中断循环: package mainimport ("fmt" )func …...

11. 瀑布流布局
<!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8" /><meta name"viewport" content"widthdevice-width, initial-scale1.0" /><title>11.瀑布流布局</title><style>#cont…...
Flutter-发布插件到pub上传不上问题
问题1: 尝试指令: flutter packages pub publish --serverhttps://pub.dartlang.org问题2: 问题1解决后,进入验证身份,点击终端显示的链接,跳转到google验证,记得这里要科*学上网,点…...
Windows 2008虚拟机安装、安装VM Tools、快照和链接克隆、添加硬盘修改格式为GPT
一、安装vmware workstation软件 VMware workstation的安装介质,获取路径: 链接:https://pan.baidu.com/s/1AUAw_--yjZAUPbsR7StOJQ 提取码:umz1 所在目录:\vmware\VMware workstation 15.1.0 1.找到百度网盘中vmwa…...
c++的学习之路:12、vector(1)
这章主要是根据cplusplus中的文档进行使用Vector,文章末附上测试代码。 目录 一、什么是vector 二、vector的简单使用 三、代码 一、什么是vector 下图是cplusplus的简介,上面一共有六点,如下: 1、vector是表示可变大小数组…...

2024.2.17力扣每日一题——N叉树的层序遍历
2024.2.17 题目来源我的题解方法一 广度优先搜索(队列实现) 题目来源 力扣每日一题;题序:429 我的题解 方法一 广度优先搜索(队列实现) 和二叉树的层序遍历相同,只是在添加子节点的细节有所不…...
)
滑动窗口(尺取法/Python)
滑动窗口(尺取法) 算法含义: 在解决关于区间特性的题目时保存搜索区间左右端点,然后根据实际要求不断更新左右端点位置的算法 时间复杂度: O ( n ) O(n) O(n) 空间复杂度: O ( 1 ) O(1) O(1) 在历年真题…...

【打印SQL执行日志】⭐️Mybatis-Plus通过配置在控制台打印执行日志
目录 前言 一、Mybatis-Plus 开启日志的方式 二、测试 三、日志分析 章末 前言 小伙伴们大家好,相信大家平时在处理问题时都有各自的方式,最常用以及最好用的感觉还是断点调试,但是涉及到操作数据库的执行时,默认的话在控制台…...

Vue后台管理系统常用组件的优缺点分析
以下是Vue后台管理系统常用组件的优缺点分析: Element UI 优点: 丰富的组件库:Element UI 提供了大量的组件,包括表单、表格、弹窗、导航等,可以满足各种后台管理系统的需求。易于使用:Element UI 的组件…...
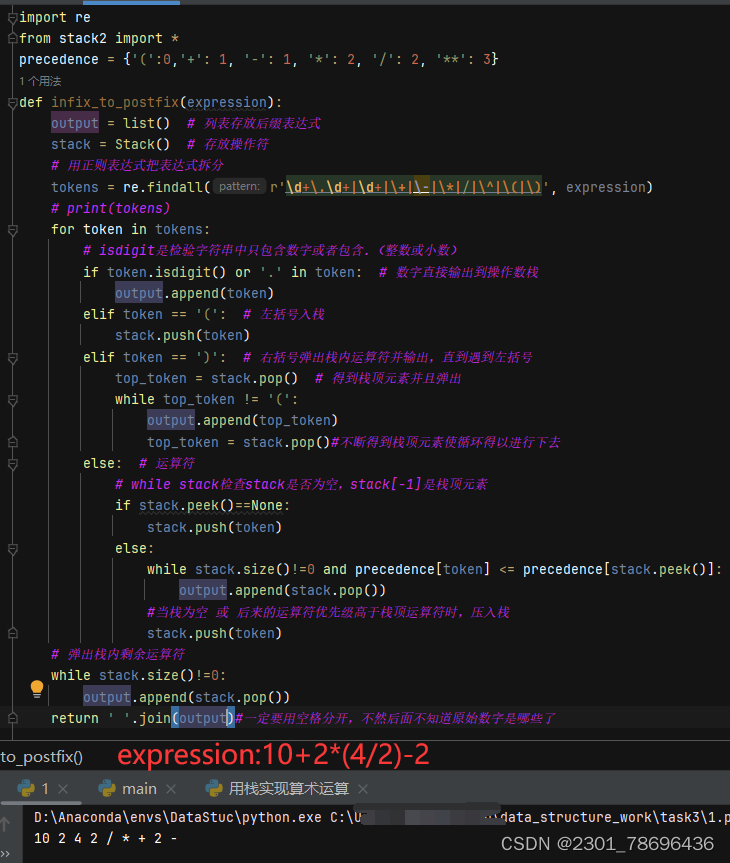
栈的应用——用栈实现算数混合运算表达式的计算
1、单目运算符双目运算符 算数运算符分为单目运算符和双目运算符等 单目运算符只需要一个操作数,双目运算符需要两个操作数 双目运算符最常见:常见的算术运算符:*/,比较运算符:<>=等等以下是一些单目运算符:正号 (+): 用于表示正数或给数值一个正号。例如:+5 仍然…...
)
动态规划—机器人移动问题(Java)
😀前言 机器人移动问题是一个经典的动态规划应用场景,它涉及到在给定范围内的位置上进行移动,并计算到达目标位置的方法数。本文将介绍三种解决这一问题的方法:暴力递归、缓存法和动态规划。通过比较不同方法的优缺点,…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...
