2024.2.17力扣每日一题——N叉树的层序遍历
2024.2.17
- 题目来源
- 我的题解
- 方法一 广度优先搜索(队列实现)
题目来源
力扣每日一题;题序:429
我的题解
方法一 广度优先搜索(队列实现)
和二叉树的层序遍历相同,只是在添加子节点的细节有所不同
时间复杂度:O(n)
空间复杂度:O(n)
public List<List<Integer>> levelOrder(Node root) {List<List<Integer>> res=new ArrayList<>();if(root==null)return res;Queue<Node> queue=new LinkedList<>();queue.offer(root);while(!queue.isEmpty()){int sz=queue.size();List<Integer> list=new ArrayList<>();for(int i=0;i<sz;i++){Node t=queue.poll();list.add(t.val);//加入子节点的细节for(Node node:t.children){queue.offer(node);}}res.add(list);}return res;
}
有任何问题,欢迎评论区交流,欢迎评论区提供其它解题思路(代码),也可以点个赞支持一下作者哈😄~
相关文章:

2024.2.17力扣每日一题——N叉树的层序遍历
2024.2.17 题目来源我的题解方法一 广度优先搜索(队列实现) 题目来源 力扣每日一题;题序:429 我的题解 方法一 广度优先搜索(队列实现) 和二叉树的层序遍历相同,只是在添加子节点的细节有所不…...
)
滑动窗口(尺取法/Python)
滑动窗口(尺取法) 算法含义: 在解决关于区间特性的题目时保存搜索区间左右端点,然后根据实际要求不断更新左右端点位置的算法 时间复杂度: O ( n ) O(n) O(n) 空间复杂度: O ( 1 ) O(1) O(1) 在历年真题…...

【打印SQL执行日志】⭐️Mybatis-Plus通过配置在控制台打印执行日志
目录 前言 一、Mybatis-Plus 开启日志的方式 二、测试 三、日志分析 章末 前言 小伙伴们大家好,相信大家平时在处理问题时都有各自的方式,最常用以及最好用的感觉还是断点调试,但是涉及到操作数据库的执行时,默认的话在控制台…...

Vue后台管理系统常用组件的优缺点分析
以下是Vue后台管理系统常用组件的优缺点分析: Element UI 优点: 丰富的组件库:Element UI 提供了大量的组件,包括表单、表格、弹窗、导航等,可以满足各种后台管理系统的需求。易于使用:Element UI 的组件…...
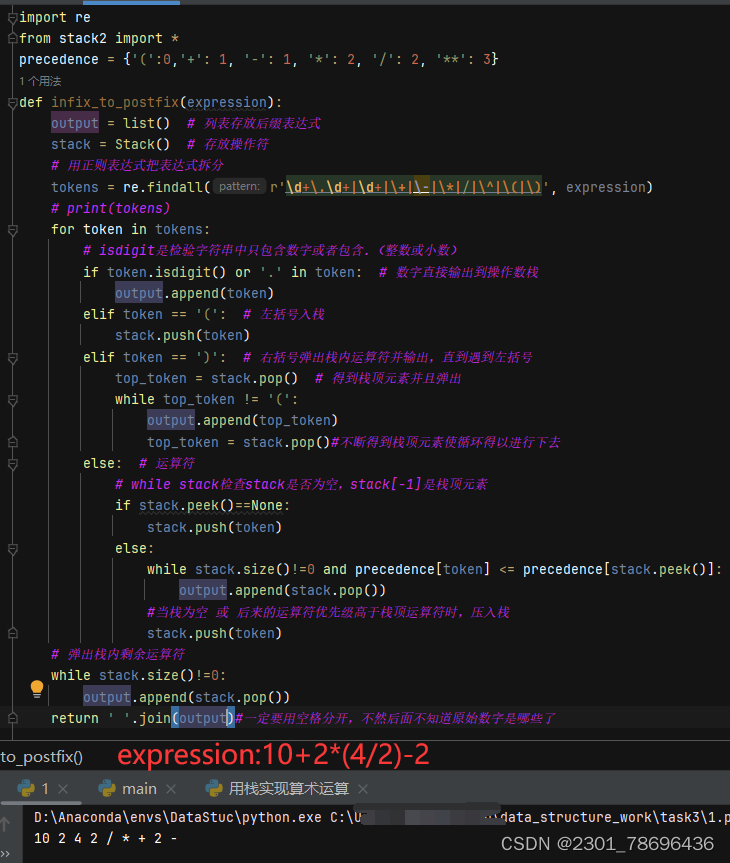
栈的应用——用栈实现算数混合运算表达式的计算
1、单目运算符双目运算符 算数运算符分为单目运算符和双目运算符等 单目运算符只需要一个操作数,双目运算符需要两个操作数 双目运算符最常见:常见的算术运算符:*/,比较运算符:<>=等等以下是一些单目运算符:正号 (+): 用于表示正数或给数值一个正号。例如:+5 仍然…...
)
动态规划—机器人移动问题(Java)
😀前言 机器人移动问题是一个经典的动态规划应用场景,它涉及到在给定范围内的位置上进行移动,并计算到达目标位置的方法数。本文将介绍三种解决这一问题的方法:暴力递归、缓存法和动态规划。通过比较不同方法的优缺点,…...

第十一届蓝桥杯物联网试题(省赛)
对于通信方面,还是终端A、B都保持接收状态,当要发送的数组不为空再发送数据,发送完后立即清除,接收数据的数组不为空则处理,处理完后立即清除,分工明确 继电器不亮一般可能是电压不够 将数据加空格再加\r…...

【Python基础教程】5. 数
🎈个人主页:豌豆射手^ 🎉欢迎 👍点赞✍评论⭐收藏 🤗收录专栏:python基础教程 🤝希望本文对您有所裨益,如有不足之处,欢迎在评论区提出指正,让我们共同学习、…...
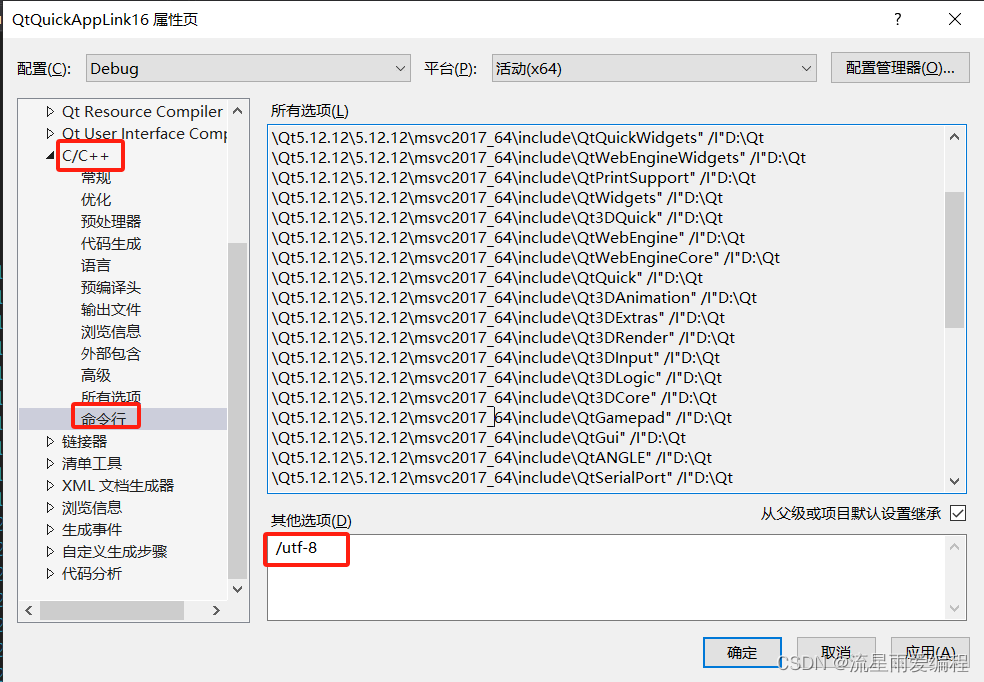
Qt中出现中文乱码的原因以及解决方法
Qt专栏:http://t.csdnimg.cn/C2SDN 目录 1.引言 2.原因分析 3.源文件的编码格式修改方法 4.程序内部使用的默认编码格式修改方法 5.QString转std::string的方法 6.总结 1.引言 在编写Qt程序的时候,或多或少都可能遇到用QString时候,明明…...

Linux 文件相关命令
一、查看文件命令 1)浏览文件less 默认查看文件的前 10 行。 less /etc/services ##功能说明: #1.默认打开首屏内容 #2.按【回车】按行访问 #3.按【空格】按屏访问 #4.【从上向下】搜索用/111,搜索包含111的内容,此时按n继续向下搜&#x…...

K8S Deployment 简介, 1个简单的Kubernetes Deployment YAML 文件
当谈到 Kubernetes 集群中的应用程序部署和管理时,Deployment、ReplicaSet 和 Pod 是三个重要的概念。它们之间存在一定的关系和层次结构。下面是对 Deployment、ReplicaSet 和 Pod 的详细解释以及它们之间的关系。 Deployment(部署) Deploy…...
win11安装WSL UbuntuTLS
win11安装WSL WSL 简介WSL 1 VS WSL 2先决要求安装方法一键安装通过「控制面板」安装 WSL 基本命令Linux发行版安装Ubuntu初始化相关设置root用户密码网络工具安装安装1panel面板指导 WSl可视化工具问题总结WSL更新命令错误Ubuntu 启动初始化错误未解决问题 WSL 简介 Windows …...

第十题:金币
题目描述 国王将金币作为工资,发放给忠诚的骑士。第一天,骑士收到一枚金币;之后两天(第二天和第三天),每天收到两枚金币;之后三天(第四、五、六天),每天收到…...

Windows 11 中Docker的安装教程
选择正确的Docker版本 在Windows上,你可以安装两种类型的Docker:Docker Desktop和Docker Toolbox。Docker Desktop是针对Windows 10 Pro、Enterprise和Education版本的,这些版本内置了Hyper-V虚拟化支持。对于旧版本的Windows,比…...
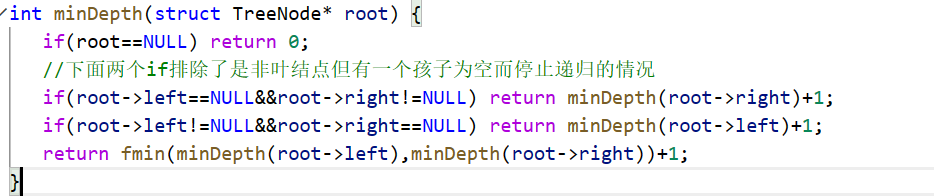
纯C代码模板
一、快排 void QuickSort(int *a,int left,int right){if(left>right) return;else{int low left,high right;int pivot a[low];while(low<high){while(a[high] > pivot && low < high){high--;}a[low] a[high]; //必须先动a[low]while(a[low] < …...
二、GitLab相关操作
GitLab相关操作 一、组、用户、项目管理1.创建组2.创建项目3.创建用户并分配组3.1 创建用户3.2 设置密码3.3 给用户分配组 二、拉取/推送代码1.配置ssh(第一次需要)1.1 创建一个空文件夹1.2 配置本地仓账号和邮箱1.3 生成ssh公钥密钥1.4 gitlab配置公钥 2.拉取代码3.推送代码3.…...

【详细注释+流程讲解】基于深度学习的文本分类 TextCNN
前言 这篇文章用于记录阿里天池 NLP 入门赛,详细讲解了整个数据处理流程,以及如何从零构建一个模型,适合新手入门。 赛题以新闻数据为赛题数据,数据集报名后可见并可下载。赛题数据为新闻文本,并按照字符级别进行匿名…...

Day.21
interface MyInterface{public final static int PI 3;void show();public default void printX(){System.out.println("接口默认方法");}public static void printY(){System.out.println("接口静态方法");}}class MyClass implements MyInterface{publi…...

Spring-IoC 基于注解
基于xml方法见:http://t.csdnimg.cn/dir8j 注解是代码中的一种特殊标记,可以在编译、类加载和运行时被读取,执行相应的处理,简化 Spring的 XML配置。 格式:注解(属性1"属性值1",...) 可以加在类上…...
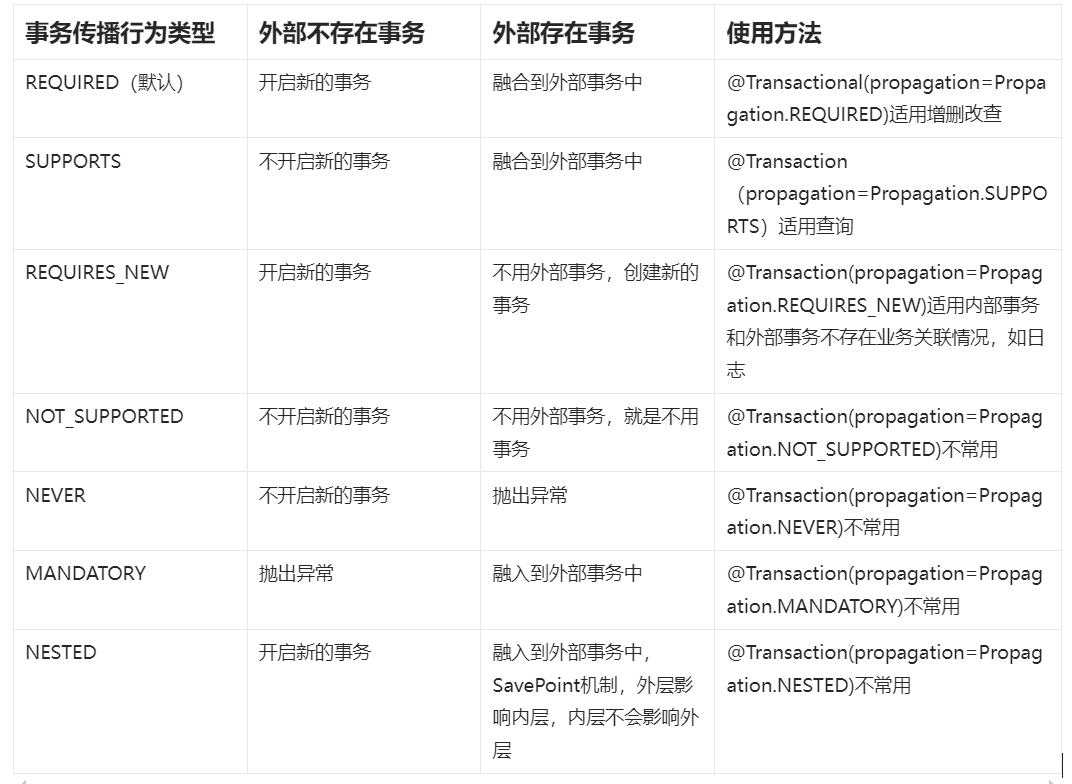
Spring声明式事务以及事务传播行为
Spring声明式事务以及事务传播行为 Spring声明式事务1.编程式事务2.使用AOP改造编程式事务3.Spring声明式事务 事务传播行为 如果对数据库事务不太熟悉,可以阅读上一篇博客简单回顾一下:MySQL事务以及并发访问隔离级别 Spring声明式事务 事务一般添加到…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...

Pydantic + Function Calling的结合
1、Pydantic Pydantic 是一个 Python 库,用于数据验证和设置管理,通过 Python 类型注解强制执行数据类型。它广泛用于 API 开发(如 FastAPI)、配置管理和数据解析,核心功能包括: 数据验证:通过…...

如何在Windows本机安装Python并确保与Python.NET兼容
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...
