红黑树路径长度分析:证明与实现
红黑树路径长度分析:证明与实现
- 一、红黑树的基本性质
- 二、证明:最长路径至多是最短路径的2倍
- 2.1 证明思路
- 2.2 证明过程
- 三、伪代码实现
- 四、 C语言代码实现
- 5、 结论
红黑树作为一种高效的自平衡二叉搜索树,在计算机科学领域中被广泛应用于各种数据结构和算法问题。它通过一系列精心设计的性质来确保树的高度始终保持在对数级别,从而保证操作的效率。本文将证明一个关于红黑树的重要性质:在一棵红黑树中,从某结点x到其后代叶结点的所有简单路径中,最长的一条至多是最短一条的2倍。此外,我们将提供伪代码和C语言代码实例,以便读者更好地理解这一性质的证明和实现。
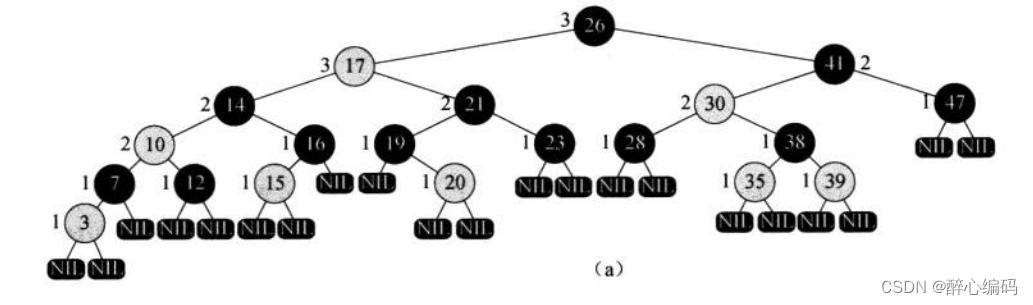
一、红黑树的基本性质
在深入讨论之前,让我们回顾一下红黑树的五个基本性质:
- 性质1:每个节点要么是红色,要么是黑色。
- 性质2:根节点是黑色的。
- 性质3:每个叶子节点(NIL节点)都是黑色的。
- 性质4:如果一个节点是红色的,则它的两个子节点都是黑色的。
- 性质5:对于每个节点,从该节点到其所有后代叶子节点的简单路径上,均包含相同数目的黑色节点。
二、证明:最长路径至多是最短路径的2倍
为了证明这一性质,我们首先需要了解红黑树的结构和性质如何影响路径的长度。考虑红黑树中的任意结点x,我们需要证明从x到其所有后代叶结点的路径中,最长路径不会超过最短路径的2倍。
2.1 证明思路
- 基于性质5:由于性质5保证了从x到每个后代叶结点的路径上黑色节点的数量相同,我们可以推断出这些路径的长度关系。
- 考虑最坏情况:最长路径可能发生在连续红色节点最多的路径上,而最短路径可能发生在没有红色节点或红色节点最少的路径上。
- 路径长度的计算:在红黑树中,路径的长度可以由黑色节点的数量决定。由于最长路径上的黑色节点数量是固定的,因此路径的长度差异主要来自于红色节点的数量。
2.2 证明过程
设结点x到其后代叶结点的最长路径上的红色节点数量为R,最短路径上的红色节点数量为r。根据红黑树的性质4,我们知道最长路径上的红色节点数量R不会超过2,因为任何红色节点的两个子节点都是黑色的。
现在,考虑最长路径和最短路径的黑色节点数量。由于性质5,这些路径上的黑色节点数量是相同的。设这个数量为B。
最长路径的长度为B + R,而最短路径的长度为B - r。由于R至多为2,我们可以得出:
最长路径长度 = B + R ≤ B + 2
最短路径长度 = B - r
因此,最长路径长度至多是最短路径长度的2倍。
三、伪代码实现
以下是计算红黑树中最长路径和最短路径长度的伪代码实现:
FUNCTION calculatePathLengths(T, x)longestPath = 0shortestPath = INFINITYblackNodesCount = 0redNodesCount = 0FUNCTION dfs(node)IF node IS NILRETURN 0ENDIFblackNodesCount += 1IF node.color == REDredNodesCount += 1ENDIFleftPath = dfs(node.left)rightPath = dfs(node.right)IF leftPath + rightPath > longestPathlongestPath = leftPath + rightPathENDIFIF leftPath < shortestPathshortestPath = leftPathENDIFRETURN blackNodesCount + (IF node.color == RED THEN 0 ELSE 1)ENDFUNCTIONdfs(x)RETURN (longestPath, shortestPath)
ENDFUNCTION
四、 C语言代码实现
下面是C语言中实现上述伪代码的示例代码:
#include <stdio.h>
#include <stdlib.h>typedef enum {RED, BLACK} Color;typedef struct Node {int key;Color color;struct Node *left, *right;
} Node;int dfs(Node *node, int *blackNodesCount, int *redNodesCount) {if (node == NULL) {return 0;}(*blackNodesCount)++;if (node->color == RED) {(*redNodesCount)++;}int leftPath = dfs(node->left, blackNodesCount, redNodesCount);int rightPath = dfs(node->right, blackNodesCount, redNodesCount);int longestPath = leftPath + rightPath;if (longestPath > *blackNodesCount + *redNodesCount) {*blackNodesCount += *redNodesCount;}return longestPath;
}int main() {// 创建和初始化树的代码// ...// 假设我们有一个红黑树T和结点xNode *T = (Node *)malloc(sizeof(Node));// 初始化T和x// ...int blackNodesCount = 0;int redNodesCount = 0;int longestPath = 0;int shortestPath = 0;// 调用dfs函数计算路径长度dfs(T, &blackNodesCount, &redNodesCount);// 输出结果printf("Longest Path: %d\n", longestPath);printf("Shortest Path: %d\n", shortestPath);// 后续操作和清理代码// ...return 0;
}
5、 结论
通过上述证明和代码实现,我们可以看到红黑树的一个重要性质:从某结点到其后代叶结点的所有简单路径中,最长的一条至多是最短一条的2倍。这一性质不仅展示了红黑树的平衡性,也为我们在实际应用中设计和优化红黑树提供了理论基础。理解并实现这一性质的证明和代码,可以帮助我们在解决数据结构和算法问题时更加自信和高效。
相关文章:

红黑树路径长度分析:证明与实现
红黑树路径长度分析:证明与实现 一、红黑树的基本性质二、证明:最长路径至多是最短路径的2倍2.1 证明思路2.2 证明过程 三、伪代码实现四、 C语言代码实现5、 结论 红黑树作为一种高效的自平衡二叉搜索树,在计算机科学领域中被广泛应用于各种…...
)
esp32 gpio初识(一)
目录 功能介绍 实操 功能介绍 引脚又叫管脚,英文叫 Pin, 就是从集成电路(芯片以及一些电子元件)内部电路引出与外围电路的接线的接口。 在我们的 ESP32 开发板上, 我们可以把这些称为引脚, 这些引脚其实是从 ESP32 芯片内部引出来的, 我们…...
)
python 自制黄金矿工游戏(设计思路+源码)
1.视频效果演示 python自制黄金矿工,细节拉满沉浸式体验,看了你也会 2.开发准备的工具 python3.8, pygame库(python3.5以上的版本应该都可以) 图片处理工具,美图秀秀 截图工具,电脑自带的 自动抠图网页:https://ko…...

Splunk Attack Range:一款针对Splunk安全的模拟测试环境创建工具
关于Splunk Attack Range Splunk Attack Range是一款针对Splunk安全的模拟测试环境创建工具,该工具完全开源,目前由Splunk威胁研究团队负责维护。 该工具能够帮助广大研究人员构建模拟攻击测试所用的本地或云端环境,并将数据转发至Splunk实例…...

OpenCV入门例程:裁剪图片、模糊检测、黑屏检测
初级代码游戏的专栏介绍与文章目录-CSDN博客 我的github:codetoys,所有代码都将会位于ctfc库中。已经放入库中我会指出在库中的位置。 这些代码大部分以Linux为目标但部分代码是纯C的,可以在任何平台上使用。 本例程运行环境为CentOS7&…...

opencv-python库 cv2边界填充resize图片
文章目录 边界填充改变图片大小 边界填充 在OpenCV中,边界填充(Border Padding)是指在图像周围添加额外的像素,以扩展图像的尺寸或满足某些算法(如卷积)的要求。OpenCV提供了cv2.copyMakeBorder()函数来进…...

Java代码基础算法练习-负数个数统计-2024.04.04
任务描述: 从键盘输入任意10个整型数(数值范围-100000~100000),统计其中的负数个数 任务要求: 代码示例: package April_2024;import java.util.Scanner;// 从键盘输入任意10个整型数(数值范围…...

【算法刷题day17】Leetcode:110.平衡二叉树 257. 二叉树的所有路径 404.左叶子之和
110.平衡二叉树 文档链接:[代码随想录] 题目链接::110.平衡二叉树 题目: 给定一个二叉树,判断它是否是 平衡二叉树 注意: 判断两棵子树高度差是否大于1 class Solution { public:int result;bool isBalanced(TreeNode…...

C++ | Leetcode C++题解之第10题正则表达式匹配
题目: 题解: class Solution { public:bool isMatch(string s, string p) {int m s.size();int n p.size();auto matches [&](int i, int j) {if (i 0) {return false;}if (p[j - 1] .) {return true;}return s[i - 1] p[j - 1];};vector<…...

职场迷航?MBTI测试为你指明方向,找到最匹配的职业!
MBTI简介 MBTI的全名是Myers-Briggs Type Indicator。它是一种迫选型、自我报告式的性格评估工具,用以衡量和描述人们在获取信息、作出决策、对待生活等方面的心理活动规律和性格类型。 类型指标 美国的凯恩琳布里格斯和她的女儿伊莎贝尔布里格斯迈尔斯研制了迈尔…...
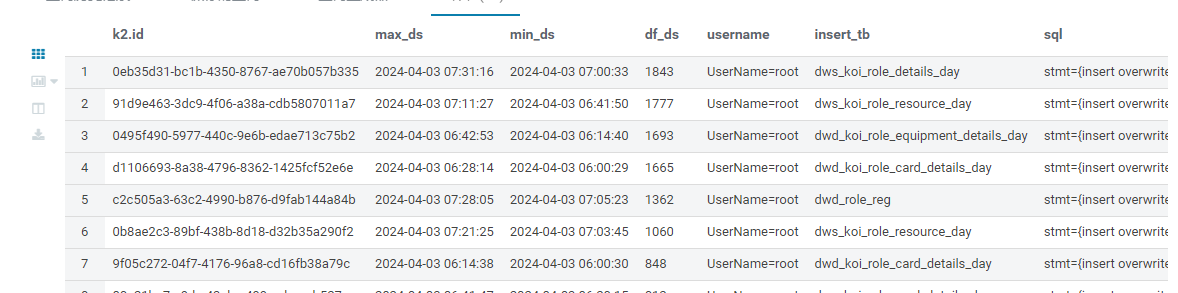
hive 慢sql 查询
hive 慢sql 查询 查找 hive 执行日志存储路径(一般是 hive-audit.log ) 比如:/var/log/Bigdata/audit/hive/hiveserver/hive-audit.log 解析日志 获取 执行时间 执行 OperationId 执行人 UserNameroot 执行sql 数据分隔符为 \001 并写入 hiv…...

Vue - 2( 10000 字 Vue 入门级教程)
一:Vue 1.1 绑定样式 1.1.1 绑定 class 样式 <!DOCTYPE html> <html><head><meta charset"UTF-8" /><title>绑定样式</title><style>......</style><script type"text/javascript" src&…...
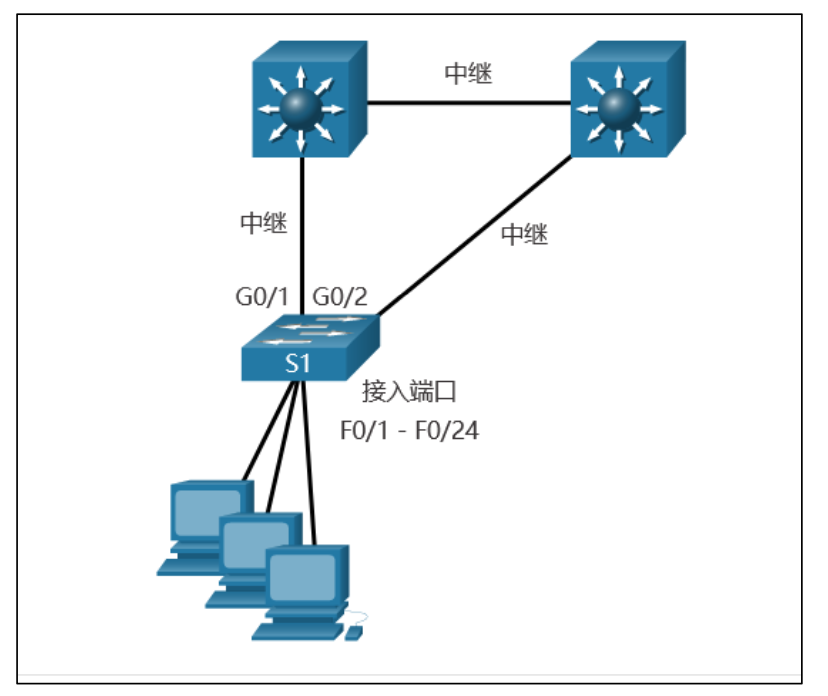
Cisco交换机安全配置
Cisco交换机安全配置 前提 我们以下命令一般都要先进入Config模式 S1> enable S1# conf t S1(config)#端口安全保护 禁用未使用的端口 以关闭fa0/1到fa0/24的端口为例 S1(config)# interface range fa0/1-24 S1(config-if-range)# shutdown缓解MAC地址表攻击 防止CAM…...
LLM大模型可视化-以nano-gpt为例
内容整理自:LLM 可视化 --- LLM Visualization (bbycroft.net)https://bbycroft.net/llm Introduction 介绍 Welcome to the walkthrough of the GPT large language model! Here well explore the model nano-gpt, with a mere 85,000 parameters. 欢迎来到 GPT 大…...

【layui-table】转静态表格时固定表格列处理行高和单元格颜色
处理思路:覆盖layui部分表格样式 行高处理:获取当前行数据单元格的最高高度,将当前行所有数据单元格高度设置为该最高高度 单元格颜色处理:将原生表格转换为layui表格后,因为原生表格的表格结构和生成的layui表格结构…...
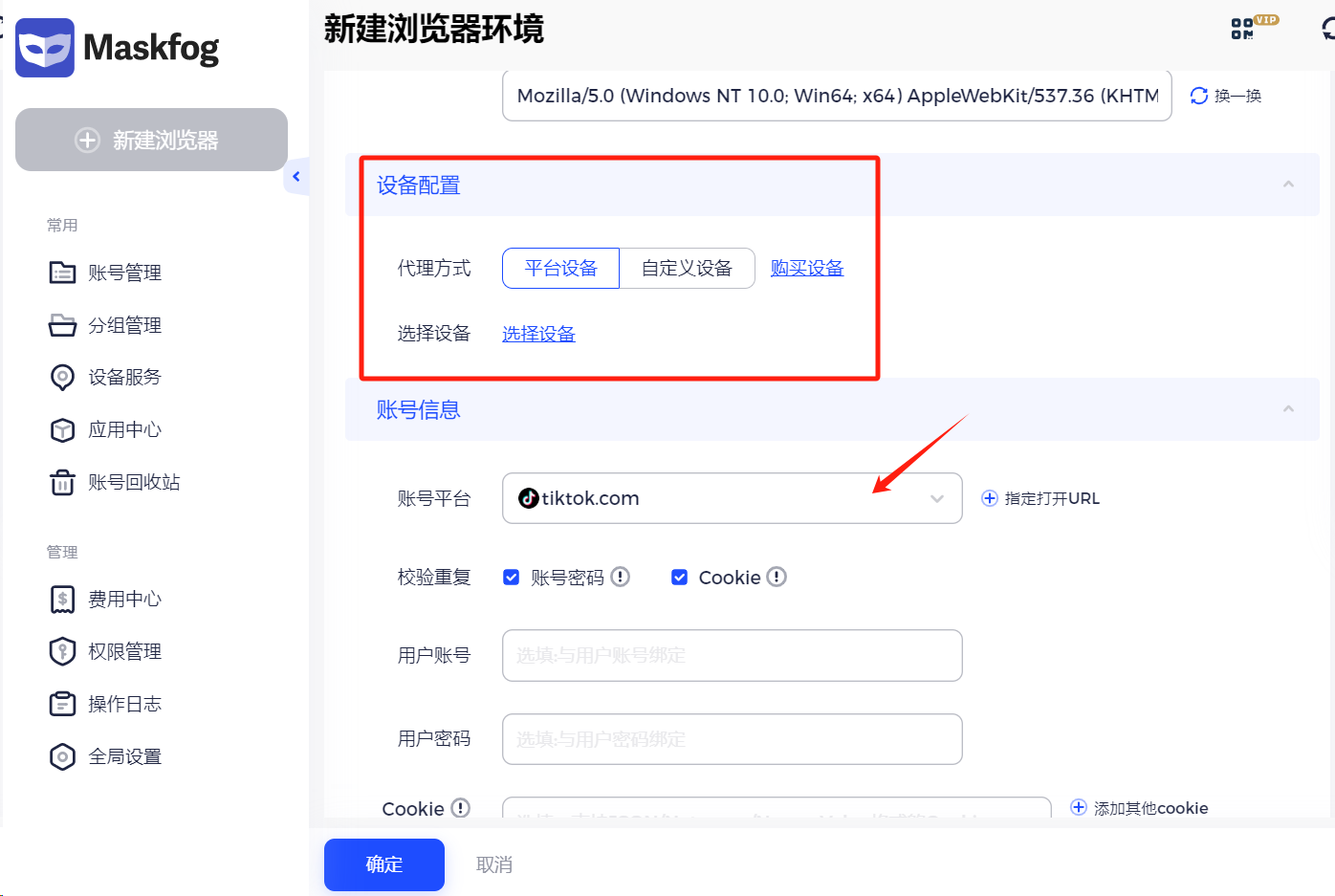
如何同时安全高效管理多个谷歌账号?
您的业务活动需要多个 Gmail 帐户吗?出海畅游,Gmail账号是少不了的工具之一,可以关联到Twitter、Facebook、Youtube、Chatgpt等等平台,可以说是海外网络的“万能锁”。但是大家都知道,以上这些平台注册多账号如果产生关…...

使用docker-tc对host容器进行限流
docker-tc是一个github开源项目,项目地址是https://github.com/lukaszlach/docker-tc。 运行docker-tc docker run -d \ --name docker-tc \ --network host \ --cap-add NET_ADMIN \ --restart always \ -v /var/run/docker.sock:/var/run/docker.sock \ -v /var…...

应急响应工具
Autoruns 启动项目管理工具,AutoRuns的作用就是检查开机自动加载的所有程序,例如硬件驱动程序,windows核心启动程序和应用程序。它比windows自带的[msconfig.exe]还要强大,通过它还可以看到一些在msconfig里面无法查看到的病毒和…...

PostgreSQL 文章下架 与 热更新和填充可以提升数据库性能
开头还是介绍一下群,如果感兴趣PolarDB ,MongoDB ,MySQL ,PostgreSQL ,Redis, Oceanbase, Sql Server等有问题,有需求都可以加群群内有各大数据库行业大咖,CTO,可以解决你的问题。加群请联系 liuaustin3 ,(…...

什么是 内网穿透
内网穿透是一种技术手段,用于在内部网络(如家庭网络或公司网络)中的设备能够被外部网络访问和控制。它允许将位于私有网络中的设备暴露在公共网络(如互联网)上,从而实现远程访问和管理。 内网穿透通常通过…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...
