蓝桥杯(5):python动态规划DF[2:背包问题]
1 0-1背包介绍【每件物品只能拿1件或者不拿】
1.1 简介


贪心是不可以的!!!

1.2 状态 及状态转移


转移解释:要么不选 则上一个直接转移过来【dp[i-1][j]】,要么是选这个之后体积为j 则上一个对应的就是【dp[i-1][j-wi] + v[i]】 选上这个之后价值叫上哦!!1
1.3 代码

n,v= list(map(int,input().split()))
w = [0]
value = [0]
for i in range(n):w_v = list(map(int,input().split()))w.append(w_v[0])value.append((w_v[1]))
# print(w)
# print(value)
'''容量总共为V
不超过v的时候价值最大
求最大价值--是矩阵中的值,那么还有两个指标分别是 物品数和容量
dp[i][j]表示前i个物品当体积为j时对应的价值''''''找到状态之后 想状态转移方程:
如果第i个物品不拿 dp[i][j] = dp[i-1][j]
如果第i个物品拿 dp[i][j] = dp[i-1][j-w[i]]+value[i]
要最大的价值 则选最大的 决定拿还是不拿'''
dp = [[0]*(v+1) for i in range(n+1)]
for i in range(1,n+1):for j in range(1,v+1):if j>=w[i]: # 说明存在第i个拿出来这种情况dp[i][j] = max(dp[i-1][j], dp[i-1][j-w[i]]+value[i])else:dp[i][j] = dp[i-1][j]print(dp[n][v])
2 滚动数组优化
发现在上方的代码中 更新第i行只用到了i-1行的数据,所有可以把空间压缩为2
然后对代码做以下改变即可

3 完全背包【每件物品可以拿0件1件2件一直到无数件】
3.1 定义
每个物品可以不拿或者拿一件 两件。。。这样

有三个参数了现在,依次枚举i,j,k 三重循环时间代价太大了

怎么优化时间呢?

![]()
3.2 代码实现

n,v= list(map(int,input().split()))
w = [0]
value = [0]
for i in range(n):w_v = list(map(int,input().split()))w.append(w_v[0])value.append((w_v[1]))
# print(w)
# print(value)dp = [[0]*(v+1) for i in range(n+1)]
for i in range(1,n+1):for j in range(1,v+1):if j>=w[i]: # 说明存在第i个拿出来这种情况dp[i][j] = max(dp[i-1][j], dp[i][j-w[i]]+value[i])else:dp[i][j] = dp[i-1][j]print(dp[n][v])
4 多重背包【0-1背包和完全背包的结合体】
4.1 定义

每种物品可是可以多拿但是有一个上限!!

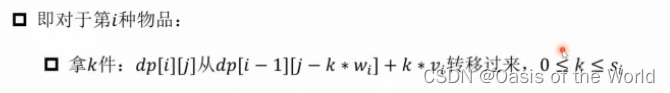
不拿的情况也包含在上面的那个式子里了,所以更新值只需要 和自己比 留下最大的即可!!!
完全背包没有办法控制上限,所以我们只能老老实实的三重循环。。。
4.2 三重循环代码
n,v= list(map(int,input().split()))
w = [0]
value = [0]
s = [0]
for i in range(n):w_v_s = list(map(int,input().split()))w.append(w_v_s[0])value.append(w_v_s[1])s.append(w_v_s[2])
# print(w)
# print(value)
'''容量总共为V
不超过v的时候价值最大
求最大价值--是矩阵中的值,那么还有两个指标分别是 物品数和容量
dp[i][j]表示前i个物品当体积为j时对应的价值''''''找到状态之后 想状态转移方程:
如果第i个物品不拿 dp[i][j] = dp[i-1][j]
如果第i个物品拿 dp[i][j] = dp[i-1][j-w[i]]+value[i]
要最大的价值 则选最大的 决定拿还是不拿'''
dp = [[0]*(v+1) for i in range(n+1)]
for i in range(1,n+1):for j in range(1,v+1):for m in range(0, min(s[i],j//w[i])+1):# if j >= m*w[i]: # 说明存在第i个拿出来这种情况dp[i][j] = max(dp[i][j], dp[i-1][j-m*w[i]]+m*value[i])# 和0-1背包的区别就是dp[i-1][j-w[i]]变成了dp[i][j-w[i]]# else:# dp[i][j] = dp[i][j]print(dp[n][v])4.3 二进制优化后代码

新策略:二进制的拆si !!!!!!!!!!!!!
普通拆发:

二进制的拆法:



##二进制优化
import sysdef put(_w, _v):for j in range(v, _w - 1, -1):dp[j] = max(dp[j], dp[j-_w] + _v)n, v = map(int, sys.stdin.readline().split())
dp = [0]*(v + 1)
for _ in range(n):weight, value, i = map(int, sys.stdin.readline().split())tmp = 1while i >= tmp:put(weight * tmp, value * tmp)i -= tmptmp <<= 1if i > 0:put(weight * i, value * i)
print(dp[v])5 二维费用背包
5.1 定义

 、
、
状态转移方程:

空间上受不了,用滚动数组

可以把i删掉
5.2 代码

N,V,M=map(int, input().split())
dp = [[0]*(M+1) for i in range(V+1)]for i in range(1,N+1):vi,mi,wi = map(int, input().split())for j in range(V,vi-1,-1):for k in range(M,mi-1,-1):#dp[i][j][k] = max(dp[i-1][j][k], dp[i-1][j-vi][k-mi]+wi)dp[j][k] = max(dp[j][k], dp[j-vi][k-mi]+wi)
print(dp[V][M])6 分组背包

很像01背包
'''
分组背包:
每组中只能选择一个物品
状态转移方程与0-1背包一样,唯一的区别是:在更新状态时要多与自己比较一次
不用一维滚动数组优化时,遍历顺序是每组,组中每个元素,背包容量
使用一维滚动数组优化时,遍历顺序是每组,背包容量,组中每个元素(可防止组中元素被选择多次)
'''##1、没有优化空间
N,V = map(int,input().split())
dp = [[0]*(V+1) for i in range(N+1)]
# dp[i][j]表示前i组物品体积不超过j的最大价值
#最终的答案dp[N][V]for i in range(1,N+1): # 对于每个组s = int(input())for q in range(s): # 对于每个组中的每个物品w,v = map(int,input().split()) #获取每个物品的质量与价值for j in range(0,V+1): #对于当前背包容量if j< w: #分组背包更新状态时,要比其他背包多一次比较,即要与本身做一次比较dp[i][j] = max(dp[i][j], dp[i-1][j])else:dp[i][j] = max(dp[i][j],dp[i-1][j],dp[i-1][j-w] + v)print(dp[N][V])#2.两行滚动数组优化N,V = map(int,input().split())
dp = [[0]*(V+1)for i in range(2)]for i in range(1,N+1):#对于每个组s = int(input())for _ in range(s): #对于每个组中的每个物品w,v = map(int,input().split()) #获取每个物品的质量与价值for j in range(1,V+1): #对于当前背包容量if j< w: #分组背包更新状态时,要比其他背包多一次比较,即要与本身做一次比较dp[i%2][j] = max(dp[i%2][j], dp[(i-1)%2][j])else:dp[i%2][j] = max(dp[i%2][j],dp[(i-1)%2][j],dp[(i-1)%2][j-w] + v)print(dp[N%2][V])#3 一维滚动数组优化 YYDS
N,V = map(int,input().split())
dp = [0]*(V+1)
for i in range(1,N+1):#对于每个组s = int(input())group = []for _ in range(s): #对于每个组中的每个物品group.append([*map(int,input().split())])#分组包采用一维滚动数组时,需先遍历背包容量,再遍历每组每个物品的质量与价值,否则会出现一组中的物品被选择多次的情况for j in range(V,-1,-1): #对于当前背包容量for w,v in group: #获取每个物品的质量与价值if j>=w: #背包容量不能小于物品质量,不然装不了#分组背包更新状态时,要比其他背包多一次比较,即要与本身做一次比较dp[j] = max(dp[j],dp[j-w] + v)
print(dp[V])相关文章:

蓝桥杯(5):python动态规划DF[2:背包问题]
1 0-1背包介绍【每件物品只能拿1件或者不拿】 1.1 简介 贪心是不可以的!!! 1.2 状态 及状态转移 转移解释:要么不选 则上一个直接转移过来【dp[i-1][j]】,要么是选这个之后体积为j 则上一个对应的就是【dp[i-1][j-wi]…...

臻奶惠无人售货机:新零售时代的便捷消费革命
臻奶惠无人售货机:新零售时代的便捷消费革命 在新零售的浪潮中,智能无人售货机作为一个创新的消费模式,已经成为距离消费者最近的便捷购物点之一。这种模式不仅能够满足居民对消费升级的需求,还能通过建立多样化和多层次的消费体…...

4月04日,每日信息差
🎖 素材来源官方媒体/网络新闻 🎄 地震预警App被曝收10元年费,回应称仅限苹果系统 🌍 2024清明档首日票房破2亿 🌋 浙江省杭州市余杭区设立2亿元网络微短剧发展基金 🎁 抖音拟以超 7.5 亿元收购海联金汇旗下…...

C++数据结构——顺序表——数值统计
C数据结构——顺序表——数值统计 接着上一篇的顺序表模板。 输入数组,统计数组中的负数、零、正数的个数。第一个数字,表示数组有几个数,当n为0时,输入结束,不做处理。 例如: 输入6 0 1 2 3 -1 0 输出1 2 3 int main() {int n;…...
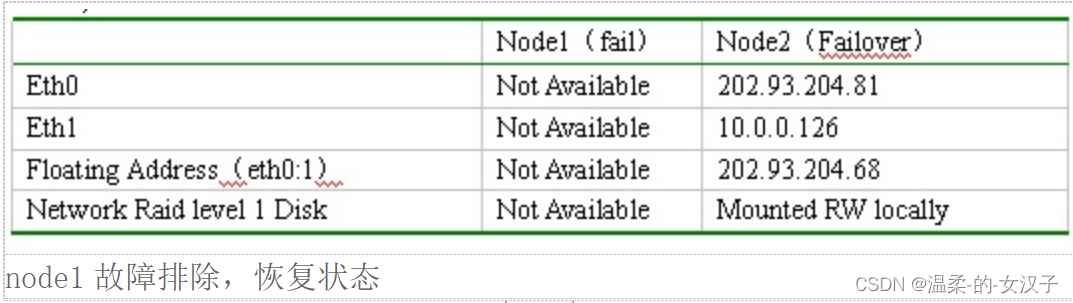
Linux+HA高可用24X7的安全保证
一. 介绍作为服务器,需要提供一定的24X7的安全保证,这样可以防止关键节点的宕机引起系统的全面崩溃。利用OpenSource开源软件,完成系统的高可靠双机热备方案。基于linux的 HA软件可靠稳定,比使用商业版本的HA软件降低成…...

【Tomcat】Apache官方结束Tomcat 8.5分支版本技术支持
根据 Apache 官方发布的声明,Apache官方将于2024年3月31日后正式结束对于Tomcat 8.5这个分支版本的技术支持,包括以下几点: 1)不太可能继续为 8.5 分支发布新的版本; 2)仅影响 8.5 分支的漏洞将不会被解决&…...

Go 源码之读写锁 sync.RWMutex
Go 源码之读写锁 sync.RWMutex 文章目录 Go 源码之读写锁 sync.RWMutex一、简介二、源码(一)RWMutex数据结构(二)Lock(三)Unlock(四)TryRLock(五)Rlock(六)RUnlock三、常见问题1. 什么是CAS,什么是原子操作2. 写操作是如何阻止写操作的3. 写操作是如何阻止读操作的…...
大数据实验统计-1、Hadoop安装及使用;2、HDFS编程实践;3、HBase编程实践;4、MapReduce编程实践
大数据实验统计 1、Hadoop安装及使用; 一.实验内容 Hadoop安装使用: 1)在PC机上以伪分布式模式安装Hadoop; 2)访问Web界面查看Hadoop信息。 二.实验目的 1、熟悉Hadoop的安装流程。 2、…...

PyTorch搭建Informer实现长序列时间序列预测
目录 I. 前言II. InformerIII. 代码3.1 输入编码3.1.1 Token Embedding3.1.2 Positional Embedding3.1.3 Temporal Embedding 3.2 Encoder与Decoder IV. 实验 I. 前言 前面已经写了很多关于时间序列预测的文章: 深入理解PyTorch中LSTM的输入和输出(从i…...

firefox切换本地服务和全球服务的方法
方法1:“设置”>“同步">“切换全球/本地服务器” https://jingyan.baidu.com/article/1974b2898523bbb5b1f774e2.html 方法2:地址栏输入about:config,搜索首选项名称里输入identity.fxaccounts.autoconfig.uri,填入…...
Windows下用CMake编译PugiXML及配置测试
作者:翟天保Steven 版权声明:著作权归作者所有,商业转载请联系作者获得授权,非商业转载请注明出处 PugiXML是什么? PugiXML 是一个用于解析和操作 XML 文档的 C 库。它提供了简单易用的接口,能够高效地加载…...

python-基础篇-字符串、列表、元祖、字典-列表
文章目录 2.3.2列表2.3.2.1列表介绍2.3.2.1.1列表的格式2.3.2.1.2打印列表 2.3.2.2列表的增删改查2.3.2.2.1列表的遍历2.3.2.2.1.1使用for循环2.3.2.2.1.2使用while循环 2.3.2.2.2添加元素("增"append, extend, insert)2.3.2.2.2.1append 2.3.2.2.2.2extend2.3.2.2.2…...
)
Qt控件样式设置其一(常见方法及优缺点)
如果你对Qt有基本的了解,应该知道它的一大优点是跨平台,可以在不同的系统中编译运行。但在我看来,Qt还有另外一个优点,就是制作界面比较方便和灵活,能够实现主流静态效果的桌面应用。(如果需要实现比较灵动…...

软件测试(测试用例详解)(三)
1. 测试用例的概念 测试用例(Test Case)是为了实施测试而向被测试的系统提供的一组集合。 测试环境操作步骤测试数据预取结果 测试用例的评价标准: 用例表达清楚,无二义性。。用例可操作性强。用例的输入与输出明确。一条用例只有…...
最优算法100例之33-字符串/数字的排列组合问题
专栏主页:计算机专业基础知识总结(适用于期末复习考研刷题求职面试)系列文章https://blog.csdn.net/seeker1994/category_12585732.html 题目描述 字符串/数字的排列组合问题 void dfs(int deep){if(deep == n){//输出}for(int i = 0; i < n; i++){if(flag[i] == 0){d[d…...

Java面试题:请解释Java中的多线程编程?
Java中的多线程编程允许 concurrently 执行多个线程,从而可以同时执行多个任务,提高程序的效率和响应性。在Java中,线程可以通过以下两种主要方式来实现: 继承 Thread 类实现 Runnable 接口 继承 Thread 类 class MyThread ext…...

acwing算法提高之图论--最小生成树的扩展应用
目录 1 介绍2 训练 1 介绍 本专题用来记录使用最小生成树算法(prim或kruskal)解决的扩展题目。 2 训练 题目1:1146新的开始 C代码如下, #include <iostream> #include <cstring> #include <algorithm>usin…...
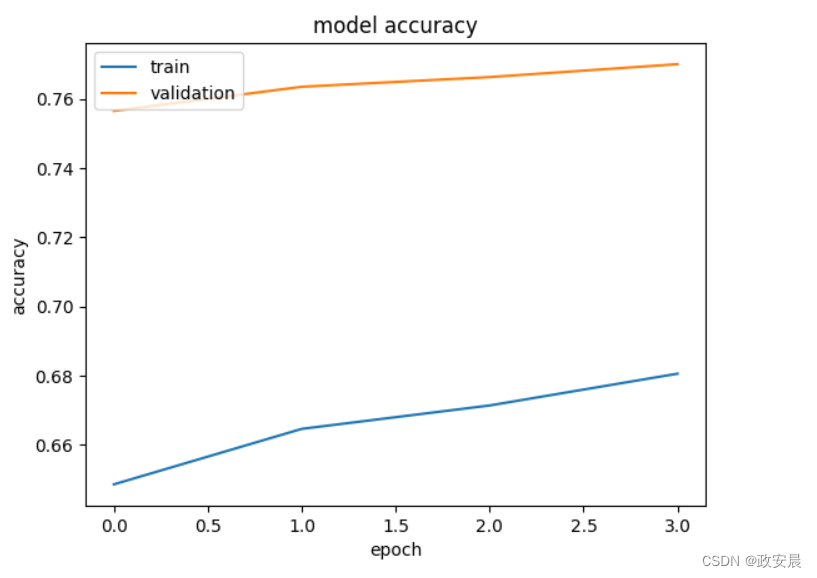
政安晨:【Keras机器学习实践要点】(十七)—— 利用 EfficientNet 通过微调进行图像分类
政安晨的个人主页:政安晨 欢迎 👍点赞✍评论⭐收藏 收录专栏: TensorFlow与Keras机器学习实战 希望政安晨的博客能够对您有所裨益,如有不足之处,欢迎在评论区提出指正! 本文目标: 使用 EfficientNet 和在图…...

wordpress全站开发指南-面向开发者及深度用户(全中文实操)--php函数
php函数 wordpress会封装一部分函数,比如bloginfo该函数的作用是直接调用你设置的你的网站的名称 示例 This is our amazing custom theme <?php echo 22; function myfirstfunction(){ echo 33; echo "<p>Hello ,this is my first function</…...
机制)
Linux 设备驱动管理之内核对象(Kernel Object)机制
Linux 设备驱动管理之内核对象(Kernel Object)机制 Linux内核是一个复杂的系统,它通过一系列的机制和结构体来管理和表示系统中的资源。其中一个关键的概念是“内核对象”(Kernel Object,简称kobject)。本文将深入探讨kobject机制…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

