统计学 一元线性回归
统计学 一元线性回归
回归(Regression):假定因变量与自变量之间有某种关系,并把这种关系用适当的数学模型表达出来,利用该模型根据给定的自变量来预测因变量
-
线性回归:因变量和自变量之间是线性关系
-
非线性回归:因变量和自变量之间是非线性关系
变量间的关系
变量间的关系:往往分为函数关系和相关关系;函数关系是确定的关系(例如 y=x2y=x^2y=x2 中 yyy 和 xxx 的关系),而相关关系是不确定的关系(例如家庭储蓄额和家庭收入)
相关系数:度量两个变量之间线性关系强度的统计量,样本相关系数记为 rrr (也称为 Pearson 相关系数),总体相关系数记为 ρ\rhoρ :
r=∑(X−Xˉ)(Y−Yˉ)∑(X−Xˉ)2⋅∑(Y−Yˉ)2r=\frac{\sum(X-\bar{X})(Y-\bar{Y})}{\sqrt{\sum(X-\bar{X})^2\cdot\sum(Y-\bar{Y})^2}} r=∑(X−Xˉ)2⋅∑(Y−Yˉ)2∑(X−Xˉ)(Y−Yˉ)
- r∈[−1,1]r\in[-1,\,1]r∈[−1,1] ,越接近 111 代表两个变量之间正线性相关关系越强,越接近 −1-1−1 代表两个变量之间负线性相关关系越强,等于 000 表示两个变量之间不存在线性关系;
- rrr 具有对称性,即 rXY=rYXr_{XY}=r_{YX}rXY=rYX ;很显然,若 XXX 与 YYY 之间是线性关系,那么 YYY 和 XXX 之间也是线性关系;
- rrr 不具有量纲,对 XXX 和 YYY 的缩放不敏感,其数值大小与 XXX 和 YYY 的尺度以及原点无关;
- rrr 不能用于描述非线性关系,可以结合散点图得出结论;
- rrr 是两个变量之间线性关系的度量,但不一定意味着 XXX 与 YYY 有因果关系。
相关系数的检验:采用 R.A.Fisher 提出的 t 分布检验,既可用于小样本,也可用于大样本:
① 提出假设:H0H_0H0 :ρ=0\rho=0ρ=0 ;H1H_1H1 :ρ=1\rho=1ρ=1 ;
② 计算样本相关系数 rrr 以及检验统计量 t=rn−21−r2∼t(n−2)t=\frac{r\sqrt{n-2}}{\sqrt{1-r^2}}\sim t(n-2)t=1−r2rn−2∼t(n−2)
③ 算出 PPP 值,进行决策
一元线性回归模型的估计
一元回归:当回归分析只涉及一个自变量时称为一元回归
回归模型:描述因变量 yyy 如何依赖于自变量 xxx 和误差项 ε\varepsilonε 的方程;一元线性回归模型可表示为:
y=β0+β1x+εy=\beta_0+\beta_1x+\varepsilon y=β0+β1x+ε
模型参数为 β0\beta_0β0 和 β1\beta_1β1 ;随机变量 ε\varepsilonε 被称为误差项,对其需要作出以下假定:
- 正态性:ε\varepsilonε 服从期望为 0 的正态分布;
- 方差齐性:对于所有的 XXX 值,ε\varepsilonε 的方差值 σ2\sigma^2σ2 都相同;
- 独立性:两个不同 XXX 值对应的 ε\varepsilonε 不相关
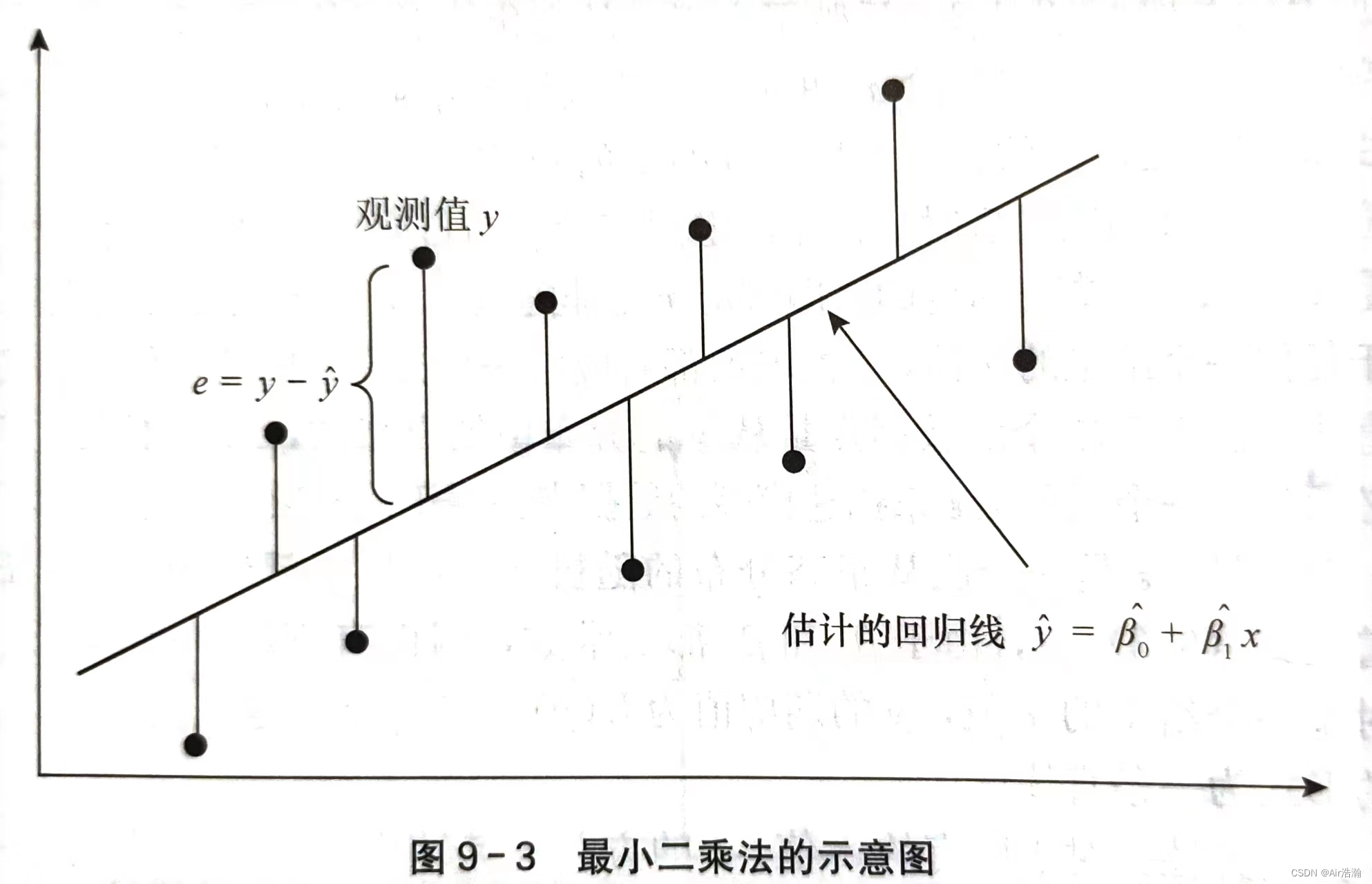
估计的回归方程:总体的 β1\beta_1β1 和 β0\beta_0β0 是未知的,需要用样本数据去估计,为:y^=β0^+β1^x\hat{y}=\hat{\beta_0}+\hat{\beta_1}xy^=β0^+β1^x (β1^\hat{\beta_1}β1^ 称为回归系数)
最小二乘法:使离差 ∣y^−y∣|\hat{y}-y|∣y^−y∣ 的平方和最小的估计方法,即:
Q=∑(yi−y^i)2=∑(yi−β^0−β1^xi)2=minQ=\sum(y_i-\hat{y}_i)^2=\sum(y_i-\hat{\beta}_0-\hat{\beta_1}x_i)^2=min Q=∑(yi−y^i)2=∑(yi−β^0−β1^xi)2=min
求导得到:
{∂Q∂β0∣β0=β^0=−2∑(yi−β^0−β^1xi)=0∂Q∂β1∣β1=β^1=−2∑xi(yi−β^0−β^1xi)=0\left\{ \begin{array}{l} \frac{\partial Q}{\partial \beta_0}\lvert_{\beta_0=\hat{\beta}_0}=-2\sum(y_i-\hat{\beta}_0-\hat{\beta}_1x_i)=0 \\ \frac{\partial Q}{\partial \beta_1}\lvert_{\beta_1=\hat{\beta}_1}=-2\sum x_i(y_i-\hat{\beta}_0-\hat{\beta}_1x_i)=0 \end{array} \right. {∂β0∂Q∣β0=β^0=−2∑(yi−β^0−β^1xi)=0∂β1∂Q∣β1=β^1=−2∑xi(yi−β^0−β^1xi)=0
解得:
{β^1=∑(x−xˉ)(y−yˉ)∑(x−xˉ)2β0^=yˉ−β^1xˉ\left\{ \begin{array}{l} \hat{\beta}_1=\frac{\sum(x-\bar{x})(y-\bar{y})}{\sum(x-\bar{x})^2} \\ \hat{\beta_0}=\bar{y}-\hat\beta_1\bar{x} \end{array} \right. {β^1=∑(x−xˉ)2∑(x−xˉ)(y−yˉ)β0^=yˉ−β^1xˉ
(最小二乘法得到的回归直线通过样本平均点 (xˉ,yˉ)(\bar{x},\,\bar{y})(xˉ,yˉ) )
一元线性回归模型的判优
拟合优度:回归直线与各观测点的接近程度称为模型的的拟合优度,评价拟合优度的一个重要统计量就是决定系数
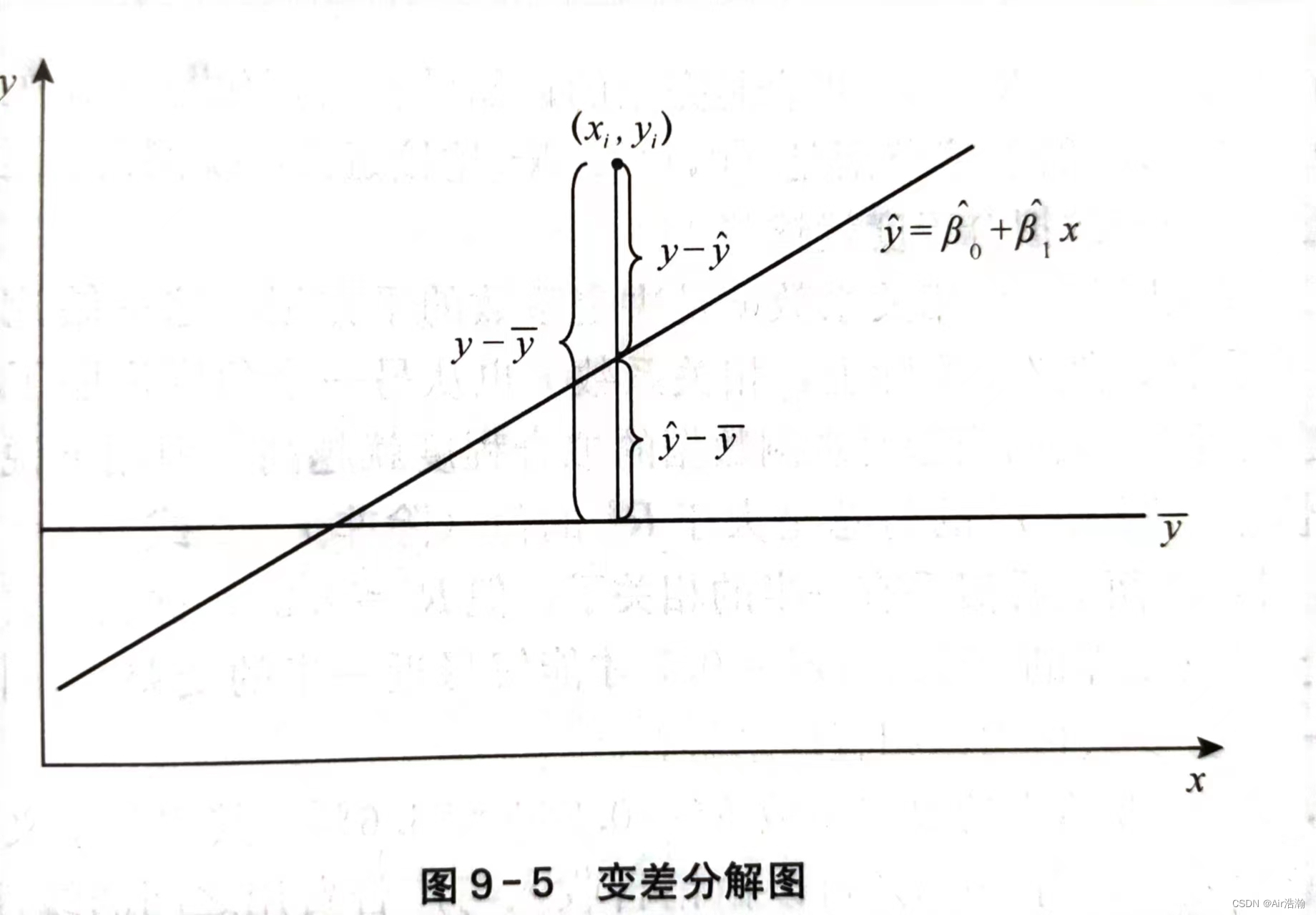
变差:因变量的取值的波动称为变差,变差的产生来自两个方面:
- 由于自变量的取值不同造成的
- 自变量以外的随机因素的影响
总平方和:nnn 次观测值的总变差可以由这些变差的平方和来表示,称为总平方和(SST),SST=∑(yi−yˉ)2SST=\sum(y_i-\bar{y})^2SST=∑(yi−yˉ)2 ;总平方和可以分解为:
SST=∑(yi−y^i+y^i−yˉ)2=∑(yi−y^i)2+∑(y^i−yˉ)2−2∑(yi−y^i)(y^i−yˉ)SST=\sum(y_i-\hat{y}_i+\hat{y}_i-\bar{y})^2=\sum(y_i-\hat{y}_i)^2+\sum(\hat{y}_i-\bar{y})^2-2\sum(y_i-\hat{y}_i)(\hat{y}_i-\bar{y}) SST=∑(yi−y^i+y^i−yˉ)2=∑(yi−y^i)2+∑(y^i−yˉ)2−2∑(yi−y^i)(y^i−yˉ)
可以证明 2∑(yi−y^i)(y^i−yˉ)=02\sum(y_i-\hat{y}_i)(\hat{y}_i-\bar{y})=02∑(yi−y^i)(y^i−yˉ)=0 ,所以总平方和实际上表现为两个部分:
{SST=∑(yi−y^i)2+∑(y^i−yˉ)2SSR=∑(y^i−yˉ)2SSE=∑(yi−y^i)2\left \{ \begin{array}{l} SST=\sum(y_i-\hat{y}_i)^2+\sum(\hat{y}_i-\bar{y})^2 \\ SSR=\sum(\hat{y}_i-\bar{y})^2 \\ SSE=\sum(y_i-\hat{y}_i)^2\\ \end{array} \right. ⎩⎨⎧SST=∑(yi−y^i)2+∑(y^i−yˉ)2SSR=∑(y^i−yˉ)2SSE=∑(yi−y^i)2
- 回归平方和(SSR):反映了 yyy 的总变差中由于 xxx 和 yyy 的线性关系引起的 yyy 的变化部分,是可以由回归直线来解释的 yiy_iyi 的变差部分
- 残差平方和(SSE) :是实际观测点与回归值的离差平方和,表示除了 xxx 对 yyy 的线性影响之外的其他随机因素对 yyy 的影响
决定系数:又称判定系数,记为 R2R^2R2 模型拟合的好坏取决于回归平方和 SSR 占总平方和 SST 的比例,越大则直线拟合得越好:
R2=SSRSST=∑(y^i−yˉ)2∑(yi−yˉ)2R^2=\frac{SSR}{SST}=\frac{\sum(\hat{y}_i-\bar{y})^2}{\sum(y_i-\bar{y})^2} R2=SSTSSR=∑(yi−yˉ)2∑(y^i−yˉ)2
在一元线性回归中,相关系数 rrr 是决定系数 R2R^2R2 的平方根
估计标准误差:即残差的标准差 ses_ese,是对误差项 ε\varepsilonε 的标准差 σ\sigmaσ 的估计,反映了实际观测值 yiy_iyi 与回归估计值 y^i\hat{y}_iy^i 之间的差异程度,ses_ese 越小,则直线拟合得越好:
se=SSEn−2=∑(yi−y^i)2n−2s_e=\sqrt{\frac{SSE}{n-2}}=\sqrt{\frac{\sum(y_i-\hat{y}_i)^2}{n-2}} se=n−2SSE=n−2∑(yi−y^i)2
一元线性回归模型的显著性检验
线性关系检验
线性关系检验:也称为 FFF 检验,用于检验自变量 xxx 和因变量 yyy 之间的线性关系是否显著,它们的关系是否能用一个线性模型 y=β0+β1x+εy=\beta_0+\beta_1x+\varepsilony=β0+β1x+ε 来表示。
- SSR 的自由度为自变量 kkk (这里一元线性回归所以 k=1k=1k=1 ),其除以自由度后得到回归均方(MSR)
- SSE 的自由度为 n−k−1n-k-1n−k−1 (这里一元线性回归所以 n−2n-2n−2),其除以自由度后得到残差均方(MSE)
① 提出检验假设:
- H0H_0H0 :β1=0\beta_1=0β1=0 (两个变量之间的线性关系不显著)
- H1H_1H1 :β1≠0\beta_1\not=0β1=0 (两个变量之间的线性关系显著)
② 计算检验自变量为
F=SSR/1SSE/(n−2)=MSRMSE∼F(1,n−2)F=\frac{SSR/1}{SSE/(n-2)}=\frac{MSR}{MSE}\sim F(1,\,n-2) F=SSE/(n−2)SSR/1=MSEMSR∼F(1,n−2)
③ 做出决策,确定显著性水平 α\alphaα ,根据自由度 df1=1df_1=1df1=1 和 df2=n−2df_2=n-2df2=n−2 得到 PPP 值,与 α\alphaα 进行比较
回归系数的检验和推断
回归系数检验:也称为 t 检验,用于检验自变量对因变量的影响是否显著;在一元线性回归模型中,回归系数检验和线性关系检验等价,而在多元线性回归中这两种检验不再等价。其检验假设为:
- H0H_0H0 :β1=0\beta_1=0β1=0 (自变量对因变量的影响不显著)
- H1H_1H1 :β1≠0\beta_1\not=0β1=0 (自变量对因变量的影响显著)
β1^\hat{\beta_1}β1^ 和 β0^\hat{\beta_0}β0^ 也是随机变量,它们有自己的抽样分布,统计证明,β1^\hat{\beta_1}β1^ 服从正态分布,期望 E(β1^)=β1E(\hat{\beta_1})=\beta_1E(β1^)=β1 ,标准差的估计量为:(ses_ese 为估计标准误差)
sβ1^=se∑xi2−1n(∑xi)2s_{\hat{\beta_1}}=\frac{s_e}{\sqrt{\sum x_i^2-\frac{1}{n}(\sum x_i)^2}} sβ1^=∑xi2−n1(∑xi)2se
(这个 sβ1^s_{\hat{\beta_1}}sβ1^ 的分母太搞了,实际上等价于 sβ^1=se∑(xi−xˉ)2s_{\hat{\beta}_1}=\frac{s_e}{\sqrt{\sum(x_i-\bar{x})^2}}sβ^1=∑(xi−xˉ)2se )
将回归系数标准化,就可以得到用于检验回归系数 β1^\hat{\beta_1}β1^ 的统计量 ttt ,在原假设成立的条件下,β1^−β1=β1^\hat{\beta_1}-\beta_1=\hat{\beta_1}β1^−β1=β1^ ,因此检验统计量为:
t=β1^sβ1^∼t(n−2)t=\frac{\hat{\beta_1}}{s_{\hat{\beta_1}}}\sim t(n-2) t=sβ1^β1^∼t(n−2)
除了对回归系数进行检验外,还可以得到置信区间,回归系数 β1\beta_1β1 在置信水平为 1−α1-\alpha1−α 下的置信区间为:
(β1^±tα/2(n−2)se∑(xi−xˉ)2)\left( \hat{\beta_1}\pm t_{\alpha/2}(n-2)\frac{s_e}{\sqrt{\sum(x_i-\bar{x})^2}} \right) (β1^±tα/2(n−2)∑(xi−xˉ)2se)
还可以得到截距 β0\beta_0β0 的 1−α1-\alpha1−α 置信区间为:
(β0^±tα/2(n−2)se1n+xˉ∑(xi−xˉ)2)\left( \hat{\beta_0}\pm t_{\alpha/2}(n-2)s_e\sqrt{\frac{1}{n}+\frac{\bar{x}}{\sum(x_i-\bar{x})^2}} \right) (β0^±tα/2(n−2)sen1+∑(xi−xˉ)2xˉ)
利用回归方程进行预测
回归分析的目的:根据所建立的回归方程,用给定的自变量来预测因变量。如果对于 xxx 的一个给定值 x0x_0x0 ,求出 yyy 的一个预测值 y^0\hat{y}_0y^0 ,就是点估计;若是求出 y0y_0y0 的一个估计区间,就是个别值的区间估计;若是求出 y0ˉ\bar{y_0}y0ˉ 的一个估计区间,就是平均值的区间估计。
例如,我们收集数据研究许多家企业的广告费支出作为自变量对销售收入这个因变量造成的影响:
- 求出广告费用为 200 万元时企业销售收入平均值的区间估计,就是平均值的区间估计;
- 求出广告费用为 200 万元的那家企业销售收入的区间估计,就是个别值的区间估计
点估计
点估计很明显,就是直接将 x0x_0x0 代入方程即可,接下来介绍平均值和个别值的预测区间。
平均值的置信区间
平均值的置信区间 :设给定因变量 xxx 的一个值 x0x_0x0 ,E(y0)E(y_0)E(y0) 为给定 x0x_0x0 时因变量 yyy 的期望值。当 x=x0x=x_0x=x0 时,y^0=β0^+β1^x0\hat{y}_0=\hat{\beta_0}+\hat{\beta_1}x_0y^0=β0^+β1^x0 就是 E(y0)E(y_0)E(y0) 的估计值。那么按照区间估计的公式,要知道 y0^\hat{y_0}y0^ 的标准差的估计量 sy0^s_{\hat{y_0}}sy0^ :
sy0^=se1n+(x0−xˉ)2∑(xi−xˉ)2s_{\hat{y_0}}=s_e\sqrt{\frac{1}{n}+\frac{(x_0-\bar{x})^2}{\sum{(x_i-\bar{x})^2}}} sy0^=sen1+∑(xi−xˉ)2(x0−xˉ)2
因此,对于给定的 x0x_0x0,平均值 E(y0)E(y_0)E(y0) 在 1−α1-\alpha1−α 置信水平下的置信区间为:
(y0^±tα/2(n−2)se1n+(x0−xˉ)2∑(xi−xˉ))\left( \hat{y_0}\pm t_{\alpha/2}(n-2)s_e\sqrt{\frac{1}{n}+\frac{(x_0-\bar{x})^2}{\sum(x_i-\bar{x})}} \right) (y0^±tα/2(n−2)sen1+∑(xi−xˉ)(x0−xˉ)2)
当 x0=xˉx_0=\bar{x}x0=xˉ 时,y^0\hat{y}_0y^0 的标准差的估计量最小,此时有 sy^0=se1ns_{\hat{y}_0}=s_e\sqrt{\frac{1}{n}}sy^0=sen1 ,也就是说当 x0=xˉx_0=\bar{x}x0=xˉ 时,估计是最准确的。x0x_0x0 偏离 xˉ\bar{x}xˉ 越远,那么 y0y_0y0 的平均值的置信区间就变得越宽,估计的效果也就越不好。
个别值的预测区间
个别值的预测区间:用 sinds_{ind}sind 表示估计 yyy 的一个个别值时 y0^\hat{y_0}y0^ 的标准差的估计量:
sind=se1+1n+(x0−xˉ)2∑(xi−xˉ)2s_{ind}=s_e\sqrt{1+\frac{1}{n}+\frac{(x_0-\bar{x})^2}{\sum{(x_i-\bar{x})^2}}} sind=se1+n1+∑(xi−xˉ)2(x0−xˉ)2
因此,对于给定的 x0x_0x0 ,yyy 的一个个别值 y0y_0y0 在 1−α1-\alpha1−α 置信水平下的预测区间为:
(y0^±tα/2(n−2)se1+1n+(x0−xˉ)2∑(xi−xˉ))\left( \hat{y_0}\pm t_{\alpha/2}(n-2)s_e\sqrt{1+\frac{1}{n}+\frac{(x_0-\bar{x})^2}{\sum(x_i-\bar{x})}} \right) (y0^±tα/2(n−2)se1+n1+∑(xi−xˉ)(x0−xˉ)2)
相比于置信区间而言,预测区间范围更宽一些,因此估计 yyy 的平均值比预测 yyy 的一个个别值更准确一些。同样,当 x0=xˉx_0=\bar{x}x0=xˉ 时,两个区间也都是最准确的。
用残差检验模型的假定
残差:e=yi−y^ie=y_i-\hat{y}_ie=yi−y^i ,表示用估计的回归方程去预测 yiy_iyi 而引起的误差
残差分析:跟方差分析一样,我们在做一元回归分析的时候也假定 y=β0+β1x+εy=\beta_0+\beta_1x+\varepsilony=β0+β1x+ε 中的误差项 ε\varepsilonε 是期望为零、具有方差齐性且相互独立的正态分布随机变量,需要对这个假设能否成立进行分析。
残差图:检验误差项 ε\varepsilonε 是否满足这些假设,可以通过对残差图的分析来完成。常用的残差图有关于 xxx 的残差图、标准化残差图等。
- 关于 xxx 的残差图是用横坐标表示自变量 xix_ixi 的值,纵轴表示对应的残差 eie_iei
检验方差齐性
如果满足方差齐性,则残差图中的所有点都应当落在同一水平带中(图 a)且没有固定的模式,否则称为异方差性(图 b)。如果出现图 c 的情况,那么应当考虑非线性回归:
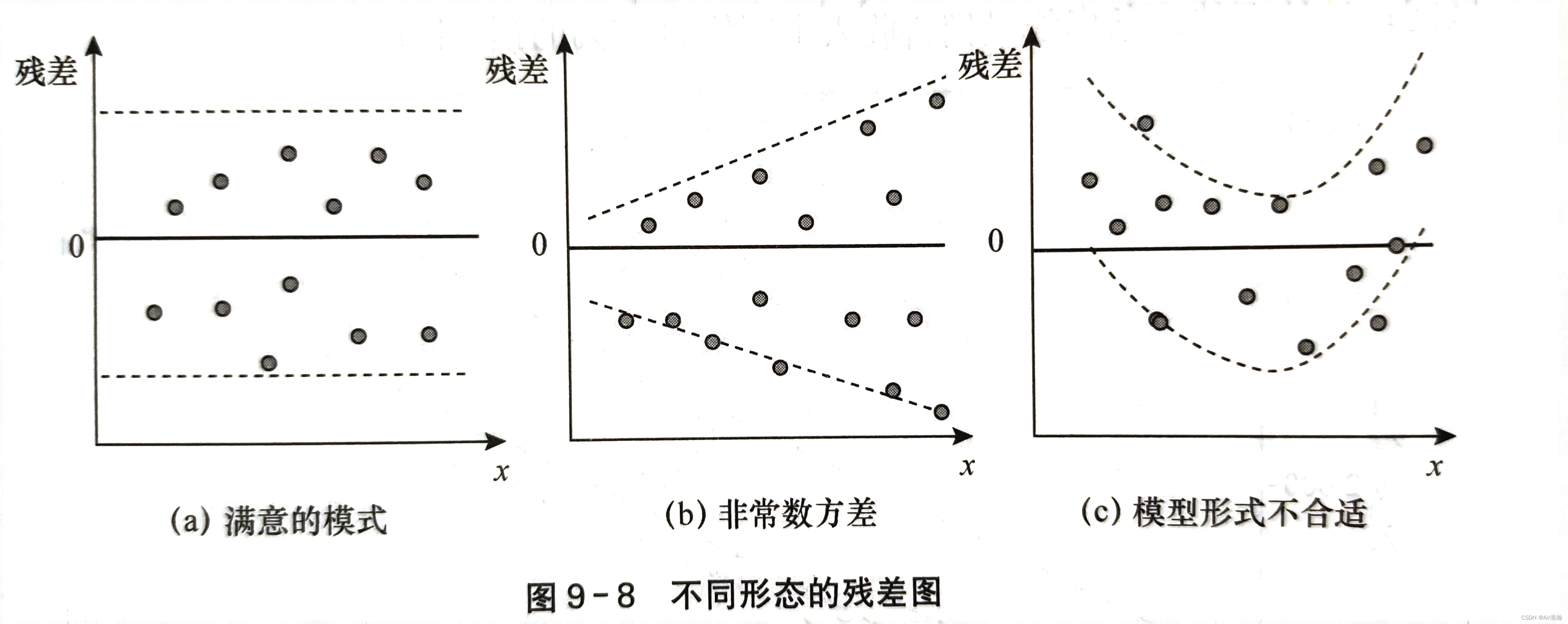
检验正态性
标准化残差:也称 Pearson 残差或半 t 化残差,是残差除以其标准差后得到的结果:
zei=eise=yi−y^isez_{e_i}=\frac{e_i}{s_e}=\frac{y_i-\hat{y}_i}{s_e} zei=seei=seyi−y^i
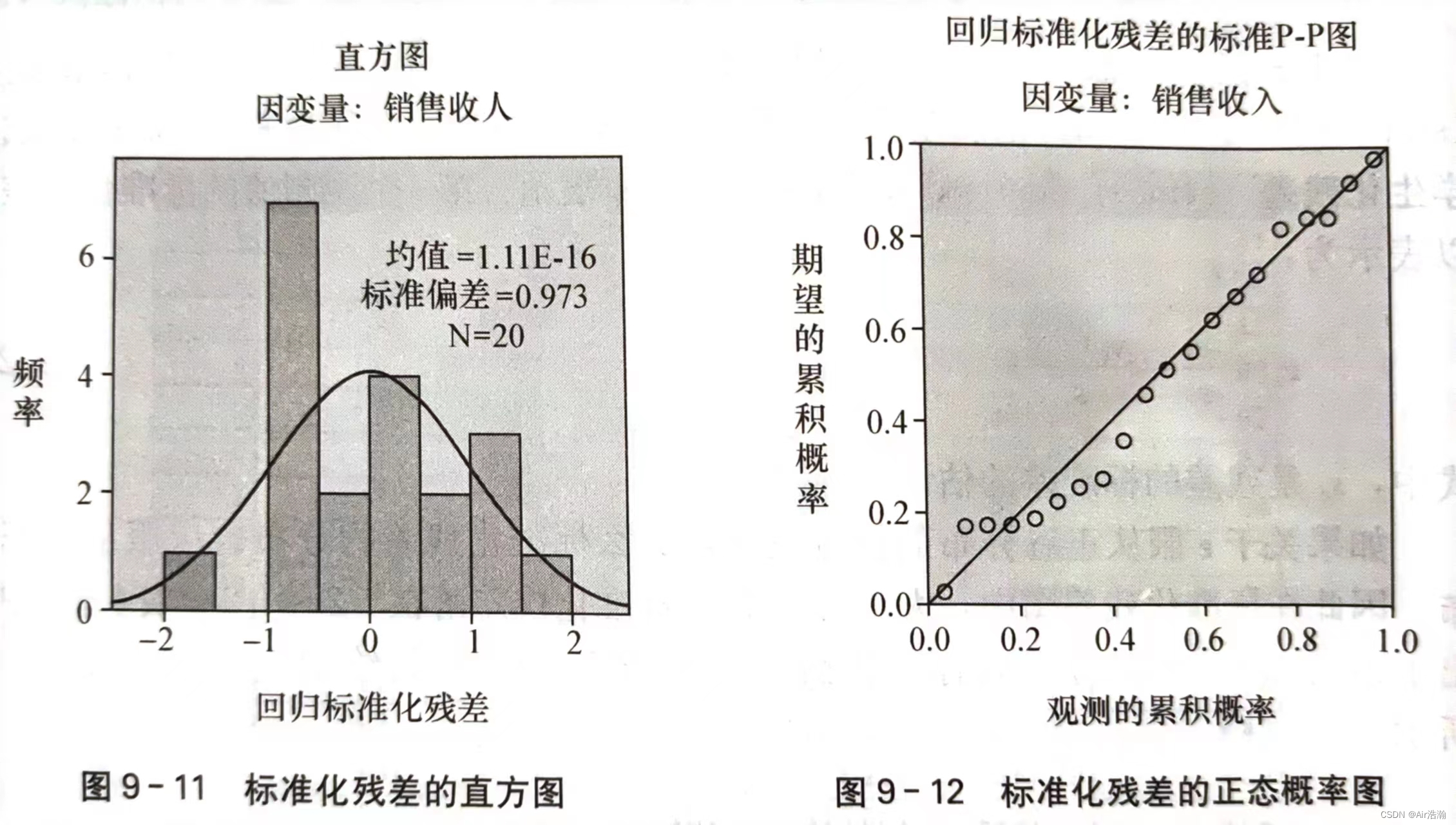
关于正态性的检验可以用标准化残差分析来完成。如果 ε\varepsilonε 服从正态分布,那么标准化残差的分布也应服从正态分布。例如,标准化后,应当有 95%95\%95% 的残差都落在 [−2,2][-2,2][−2,2] 之间:
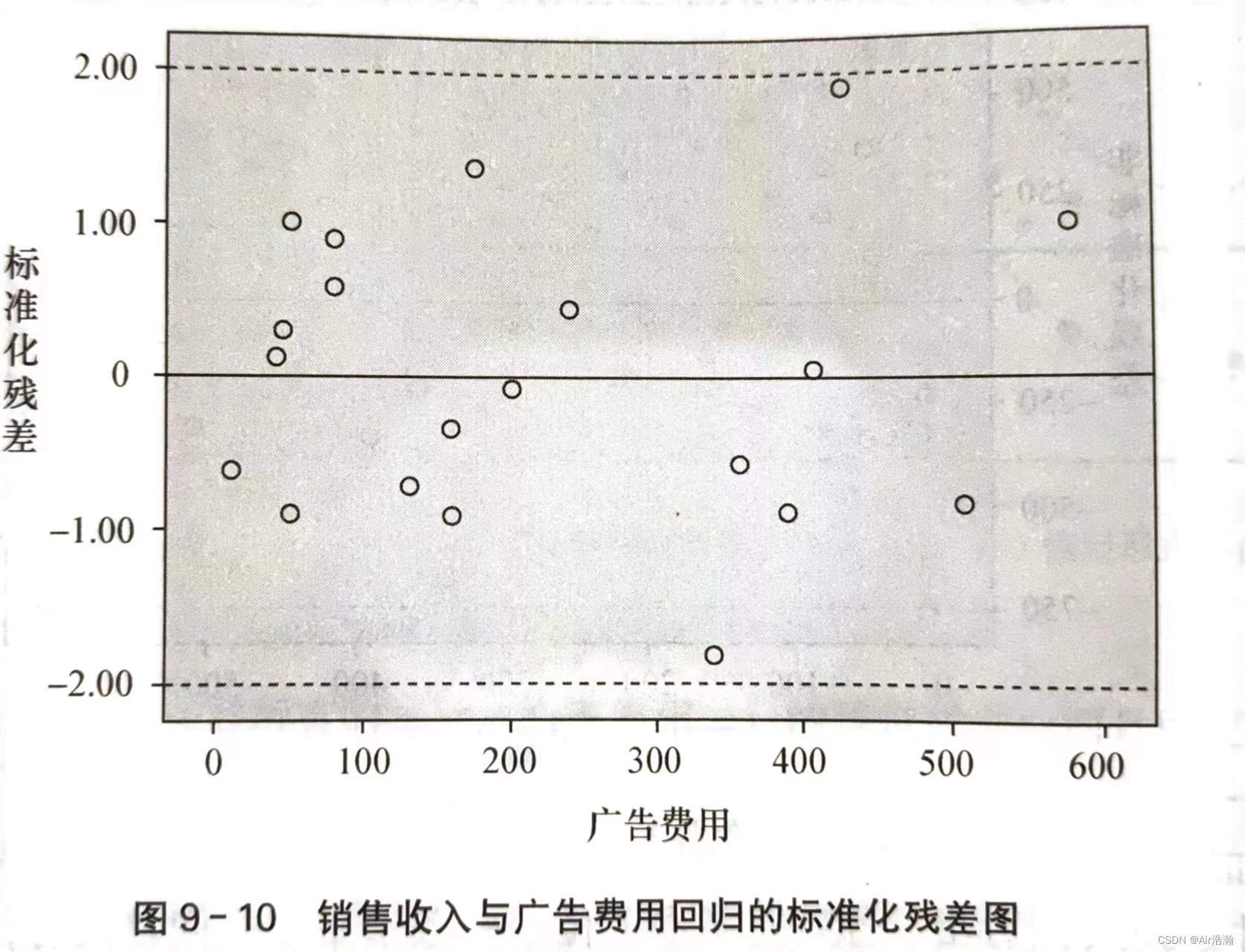
也可以画直方图或者 P-P 图来检验:
相关文章:

统计学 一元线性回归
统计学 一元线性回归 回归(Regression):假定因变量与自变量之间有某种关系,并把这种关系用适当的数学模型表达出来,利用该模型根据给定的自变量来预测因变量 线性回归:因变量和自变量之间是线性关系 非线…...

【软件开发】基于PyQt5开发的标注软件
这里是基于PyQt5写的面向目标检测的各类标注PC端软件系统。目前现有的labelme软件和labelImg开源软件无法满足特殊数据集的标注要求,而且没有标注顺序的报错提示。当然我设计的软件就会不具有适用性了(毕竟从下面开发的软件可以明显看出来我做的基本上是…...

CSS3新特性
CSS3新特性前言css3选择器边框特性背景参考前言 css3作为css的升级版本,css3提供了更加丰富实用的规范。新特性有: css3选择器边框特性多背景图颜色与透明度多列布局与弹性盒模型布局盒子的变形过渡与动画web字体媒体查询阴影 css3选择器 css3选择器…...

35 openEuler搭建repo(yum)服务器-创建、更新本地repo源
文章目录35 openEuler搭建repo(yum)服务器-创建、更新本地repo源35.1 获取ISO发布包35.2 挂载ISO创建repo源35.3 创建本地repo源35.4 更新repo源35 openEuler搭建repo(yum)服务器-创建、更新本地repo源 使用mount挂载,…...
【三.项目引入axios、申明全局变量、设置跨域】
根据前文《二.项目使用vue-router,引入ant-design-vue的UI框架,引入less》搭建好脚手架后使用 需求: 1.项目引入axios 2.申明全局变量 3.设置跨域 简介:axios本质上还是对原生XMLHttpRequest的封装,可用于浏览器和nodejs的HTTP客…...

启动u盘还原成普通u盘(Windows Diskpart)
使用windows系统的diskpart 命令解决系统盘恢复成普通U盘的问题:1. 按Windows R键打开运行窗口。在搜索框中输入“ Diskpart ”,然后按 Enter 键。2. 现在输入“ list disk ”并回车。3. 然后输入“ select disk X ”(将 X 替换为可启动U盘的…...
深入理解机器学习——偏差(Bias)与方差(Variance)
分类目录:《深入理解机器学习》总目录 偏差(Bias)与方差(Variance)是解释学习算法泛化性能的一种重要工具。偏差方差分解试图对学习算法的期望泛化错误率进行拆解,我们知道,算法在不同训练集上学…...

分布式新闻项目实战 - 13.项目部署_持续集成(Jenkins) ^_^ 完结啦 ~
欲买桂花同载酒,终不似,少年游。 系列文章目录 项目搭建App登录及网关App文章自媒体平台(博主后台)自媒体文章审核延迟任务kafka及文章上下架App端文章搜索后台系统管理Long类型精度丢失问题定时计算热点文章(xxl-Job…...

Linux c/c++技术方向分析
一、C与C介绍 1.1 说明 c语言是一门面向过程的、抽象化的通用程序设计语言,广泛应用于底层开发,如嵌入式。C语言能以简易的方式编译、处理低级存储器。是一种高效率程序设计语言。 c(c plus plus)是一种计算机高级程序设计语言&a…...
JavaScript 高级3 :函数进阶
JavaScript 高级3 :函数进阶 Date: January 19, 2023 Text: 函数的定义和调用、this、严格模式、高阶函数、闭包、递归 目标: 能够说出函数的多种定义和调用方式 能够说出和改变函数内部 this 的指向 能够说出严格模式的特点 能够把函数作为参数和返…...
【项目】Java树形结构集合分页,java对list集合进行分页
Java树形结构集合分页需求难点实现第一步:查出所有树形集合数据 (需进行缓存处理)selectTree 方法步骤:TreeUtil类:第二步:分页 GoodsCategoryController分页getGoodsCategoryTree方法步骤:第三…...
java.lang.IllegalArgumentException: itemView may not be null
报错截图:场景介绍:在使用recycleView 自动递增数据,且自动滚动到最新行; 当数据达到273条 时出现ANR;项目中 全部的列表适配器使用的三方库:BaseRecyclerViewAdapterHelper (很早之前的项目&am…...
[ 攻防演练演示篇 ] 利用 shiro 反序列化漏洞获取主机权限
🍬 博主介绍 👨🎓 博主介绍:大家好,我是 _PowerShell ,很高兴认识大家~ ✨主攻领域:【渗透领域】【数据通信】 【通讯安全】 【web安全】【面试分析】 🎉点赞➕评论➕收藏 养成习…...

达人合作加持品牌布局,3.8女神玩转流量策略!
随着迅猛发展的“她经济”,使社区本就作为内容种草的平台,自带“营销基因”。在3.8女神节即将到来之际,如何充分利用平台女性资源优势,借助达人合作等手段,实现迅速引流,来为大家详细解读下。一、小红书节日…...
观点丨Fortinet谈ChatGPT火爆引发的网络安全行业剧变
FortiGuard报告安全趋势明确指出“网络攻击者已经开始尝试AI手段”,ChatGPT的火爆之际的猜测、探索和事实正在成为这一论断的佐证。攻守之道在AI元素的加持下也在悄然发生剧变。Fortinet认为在攻击者利用ChatGPT等AI手段进行攻击的无数可能性的本质,其实…...

工业企业用电损耗和降损措施研究
来自用电设备和供配电系统的电能损耗。而供配电系统的电能损耗,包括企业变配电设备、控制设备企业在不断降低生产成本,追求经济效益的情况下,进一步降低供配电系统中的电能损耗,使电气设摘要:电网电能损耗是一个涉及面很广的综合性问题,主要包括管理损耗和技术损耗两部分…...

高并发、高性能、高可用
文章目录一、高并发是什么?二、 高性能是什么三、 高可用什么是一、高并发是什么? 示例:高并发是现在互联网分布式框架设计必须要考虑的因素之一,它是可以保证系统能被同时并行处理很多请求,对于高并发来说࿰…...
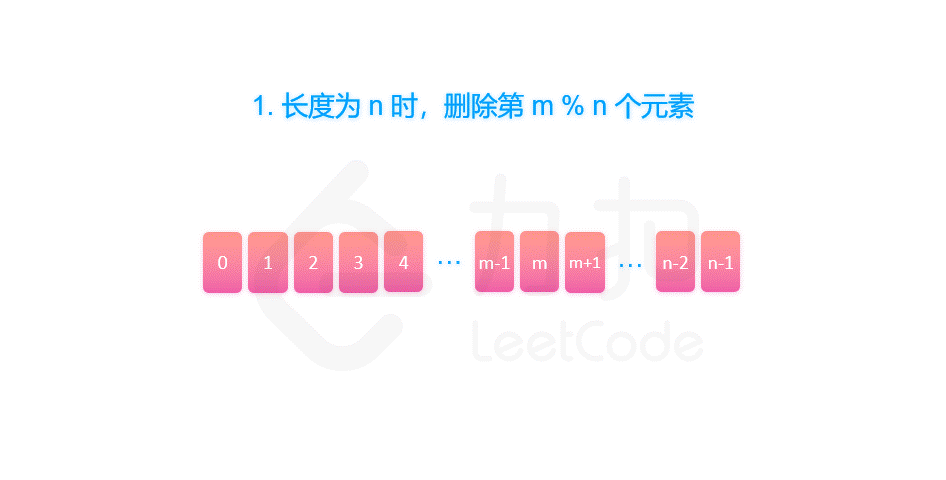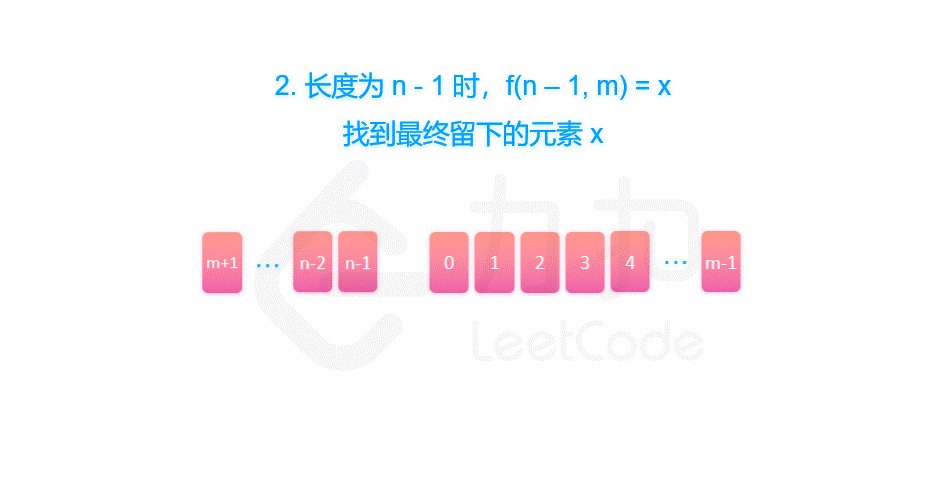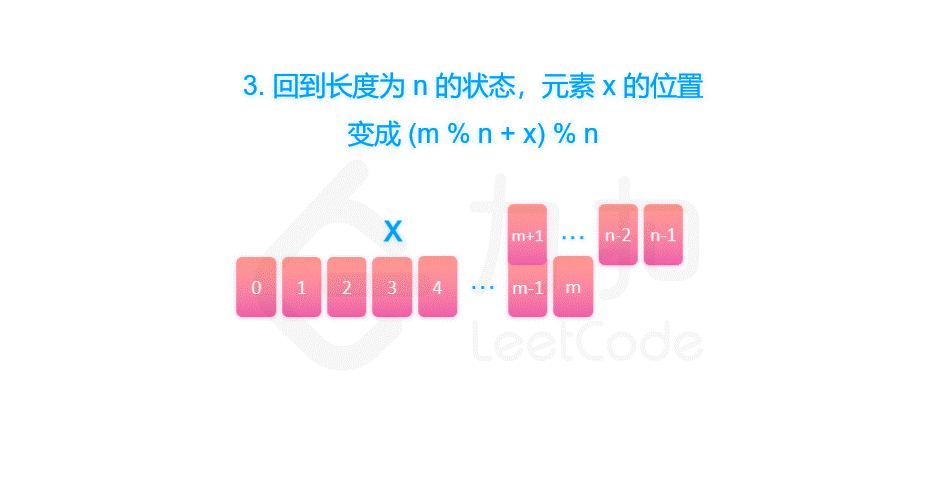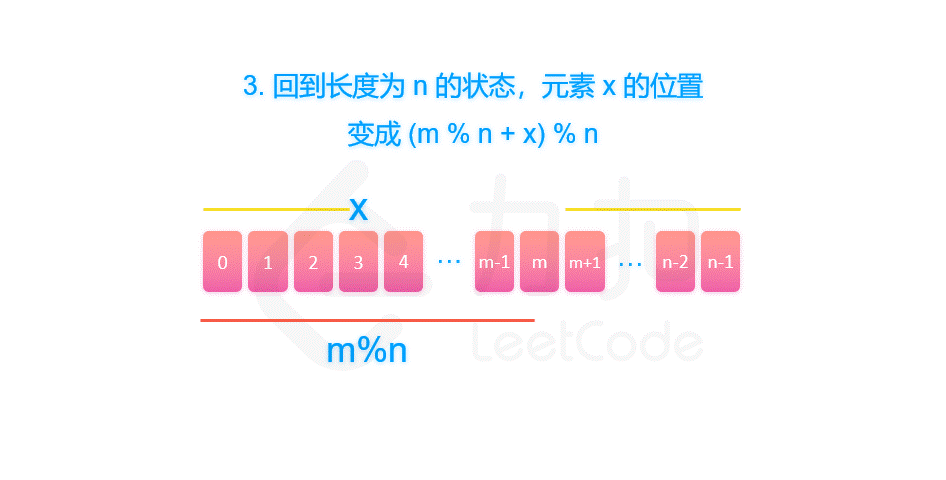
剑指 Offer 62. 圆圈中最后剩下的数字
摘要 剑指 Offer 62. 圆圈中最后剩下的数字 一、约瑟夫环解析 题目中的要求可以表述为:给定一个长度为 n 的序列,每次向后数 m 个元素并删除,那么最终留下的是第几个元素?这个问题很难快速给出答案。但是同时也要看到ÿ…...
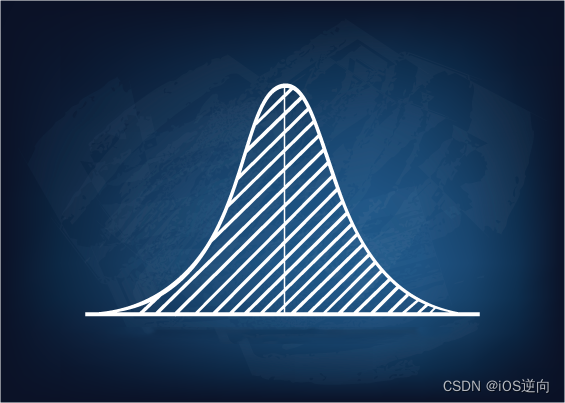
概率论小课堂:高斯分布(正确认识大概率事件)
文章目录 引言I 预备知识1.1 正态分布1.2 置信度1.3 风险II 均值、标准差和发生概率三者的关系。2.1 “三∑原则”2.2 二班成绩比一班好的可能性2.3 减小标准差引言 泊松分布描述的是概率非常小的情况下的统计规律性。学习高斯分布来正确认识大概率事件,随机变量均值的差异和偶…...

剑指 Offer 43. 1~n 整数中 1 出现的次数
摘要 剑指 Offer 43. 1~n 整数中 1 出现的次数 一、数学思维解析 将1~ n的个位、十位、百位、...的1出现次数相加,即为1出现的总次数。 设数字n是个x位数,记n的第i位为ni,则可将n写为 nxnx−1⋯n2n1: 称" …...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

DeepSeek源码深度解析 × 华为仓颉语言编程精粹——从MoE架构到全场景开发生态
前言 在人工智能技术飞速发展的今天,深度学习与大模型技术已成为推动行业变革的核心驱动力,而高效、灵活的开发工具与编程语言则为技术创新提供了重要支撑。本书以两大前沿技术领域为核心,系统性地呈现了两部深度技术著作的精华:…...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...

【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖,添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...

实战设计模式之模板方法模式
概述 模板方法模式定义了一个操作中的算法骨架,并将某些步骤延迟到子类中实现。模板方法使得子类可以在不改变算法结构的前提下,重新定义算法中的某些步骤。简单来说,就是在一个方法中定义了要执行的步骤顺序或算法框架,但允许子类…...

Linux 下 DMA 内存映射浅析
序 系统 I/O 设备驱动程序通常调用其特定子系统的接口为 DMA 分配内存,但最终会调到 DMA 子系统的dma_alloc_coherent()/dma_alloc_attrs() 等接口。 关于 dma_alloc_coherent 接口详细的代码讲解、调用流程,可以参考这篇文章,我觉得写的非常…...

Python第七周作业
Python第七周作业 文章目录 Python第七周作业 1.使用open以只读模式打开文件data.txt,并逐行打印内容 2.使用pathlib模块获取当前脚本的绝对路径,并创建logs目录(若不存在) 3.递归遍历目录data,输出所有.csv文件的路径…...
