K-means聚类
原理说明
Kmeans是一种常见的聚类算法,用于将相似的数据点归类到不同的群组中。Kmeans的原理如下:
初始化:Kmeans算法首先需要初始化一个用户指定数量的聚类中心点,通常是随机选取K个数据点作为聚类中心点。
分配:对于每个数据点,计算其到每个聚类中心点的距离,并将其分配到距离最近的聚类中心点所代表的聚类中。
更新:在所有数据点都被分配到对应的聚类中之后,重新计算每个聚类中心点的位置,即将每个聚类中的所有数据点的坐标平均值作为新的聚类中心点位置。
重复:重复步骤2和3,直到所有聚类中心点的位置不再改变,或达到预设的最大迭代次数。
输出:输出聚类结果,即每个数据点所属的聚类编号。
Kmeans算法的核心是通过最小化每个数据点到其所属聚类中心点的距离平方和来确定最优的聚类中心点位置。在实际应用中,Kmeans算法通常需要多次运行并比较结果,以获得最优的聚类结果。
原理推导
随机选择K个中心点作为簇的初始中心;
将每个数据点分配到离它最近的簇中;
计算每个簇的中心点,更新簇中心;
重复步骤2和3,直到簇中心不再发生变化或达到最大迭代次数。
下面对K-means算法进行数学推导:
设数据集为X={x1, x2, …, xn},其中每个数据点xi是一个d维向量。假设将数据点分为K个簇,第k个簇的中心点为μk,则第i个数据点与第k个簇的中心点的距离为:
dist(xi, μk) = ||xi - μk||2
其中||.||2表示欧几里得范数。
K-means算法的目标是最小化所有数据点与其所属簇中心点的距离之和,即:
J(μ1, μ2, …, μK) = ∑i=1 to n min_k{dist(xi, μk)}^2
其中min_k{.}表示求解所有K个簇中与xi距离最近的中心点μk,并将xi分配到第k个簇中。
为了求解上述目标函数J,需要对μ1, μ2, …, μK进行优化。具体而言,需要先固定簇分配,对簇中心进行优化,然后再固定簇中心,对簇分配进行优化。
对于固定簇分配,目标函数J是关于μ1, μ2, …, μK的凸函数,因此可以使用梯度下降法求解其最小值。具体而言,需要将目标函数对μk求导,即:
∂J(μ1, μ2, …, μK) / ∂μk = ∑i=1 to n 2xi(μk - xi)^T*[μk - xi = 0
其中^T表示向量的转置,即矩阵的行列互换。令上述导数等于0,得到μk的最优解:
μk = 1/Nk * ∑i∈Ck xi
其中Ck表示第k个簇中的数据点,Nk表示第k个簇中的数据点个数。
对于固定簇中心,目标函数J是关于数据点分配的离散优化问题,可以使用交替最小化法(alternating optimization)求解。具体而言,可以先随机分配数据点到簇中
具体而言,可以先随机分配数据点到簇中,然后依次更新每个簇的中心点,直到簇中心点不再发生变化或达到最大迭代次数。更新簇分配时,可以根据当前簇中心点,将每个数据点分配到距离其最近的簇中。
具体而言,假设第i个数据点当前被分配到第k个簇中,其所属簇中心为μk,则将该数据点分配到其他簇中的中心点为μl时,目标函数的变化量为:
ΔJ = ||xi - μl||2 - ||xi - μk||2
将ΔJ展开,得到:
ΔJ = ||xi||2 + ||μl||2 - 2xi^Tμl - ||xi||2 - ||μk||2 + 2xi^Tμk
ΔJ = 2(xi^Tμk - xi^Tμl + μl^Tμl - μk^Tμk)
由于将xi分配到距离其最近的簇中时,ΔJ应当小于等于0,因此可以通过比较ΔJ的大小,将xi分配到距离其最近的簇中。
综上所述,K-means算法的具体步骤如下:
随机选择K个中心点作为簇的初始中心;
将每个数据点分配到离它最近的簇中;
计算每个簇的中心点,更新簇中心;
重复步骤2和3,直到簇中心不再发生变化或达到最大迭代次数。
其中,簇分配可以使用上述交替最小化法求解,簇中心可以使用梯度下降法求解。最终的目标函数是所有数据点与其所属簇中心点的距离之和的平方,即:
J(μ1, μ2, …, μK) = ∑i=1 to n min_k{dist(xi, μk)}^2
其中dist(xi, μk) = ||xi - μk||2表示数据点xi与簇中心点μk之间的距离。
相关文章:

K-means聚类
原理说明 Kmeans是一种常见的聚类算法,用于将相似的数据点归类到不同的群组中。Kmeans的原理如下: 初始化:Kmeans算法首先需要初始化一个用户指定数量的聚类中心点,通常是随机选取K个数据点作为聚类中心点。 分配:对…...

04-SQL基础(表管理,约束,多表连接,子查询)
本文章主要内容 1、表的管理:创建表,修改表结构,删除字段,修改字段,添加字段,删除表,添加表约束; 2、数据管理:新增记录,修改记录,删除记录&…...
统计学 一元线性回归
统计学 一元线性回归 回归(Regression):假定因变量与自变量之间有某种关系,并把这种关系用适当的数学模型表达出来,利用该模型根据给定的自变量来预测因变量 线性回归:因变量和自变量之间是线性关系 非线…...

【软件开发】基于PyQt5开发的标注软件
这里是基于PyQt5写的面向目标检测的各类标注PC端软件系统。目前现有的labelme软件和labelImg开源软件无法满足特殊数据集的标注要求,而且没有标注顺序的报错提示。当然我设计的软件就会不具有适用性了(毕竟从下面开发的软件可以明显看出来我做的基本上是…...

CSS3新特性
CSS3新特性前言css3选择器边框特性背景参考前言 css3作为css的升级版本,css3提供了更加丰富实用的规范。新特性有: css3选择器边框特性多背景图颜色与透明度多列布局与弹性盒模型布局盒子的变形过渡与动画web字体媒体查询阴影 css3选择器 css3选择器…...

35 openEuler搭建repo(yum)服务器-创建、更新本地repo源
文章目录35 openEuler搭建repo(yum)服务器-创建、更新本地repo源35.1 获取ISO发布包35.2 挂载ISO创建repo源35.3 创建本地repo源35.4 更新repo源35 openEuler搭建repo(yum)服务器-创建、更新本地repo源 使用mount挂载,…...
【三.项目引入axios、申明全局变量、设置跨域】
根据前文《二.项目使用vue-router,引入ant-design-vue的UI框架,引入less》搭建好脚手架后使用 需求: 1.项目引入axios 2.申明全局变量 3.设置跨域 简介:axios本质上还是对原生XMLHttpRequest的封装,可用于浏览器和nodejs的HTTP客…...

启动u盘还原成普通u盘(Windows Diskpart)
使用windows系统的diskpart 命令解决系统盘恢复成普通U盘的问题:1. 按Windows R键打开运行窗口。在搜索框中输入“ Diskpart ”,然后按 Enter 键。2. 现在输入“ list disk ”并回车。3. 然后输入“ select disk X ”(将 X 替换为可启动U盘的…...
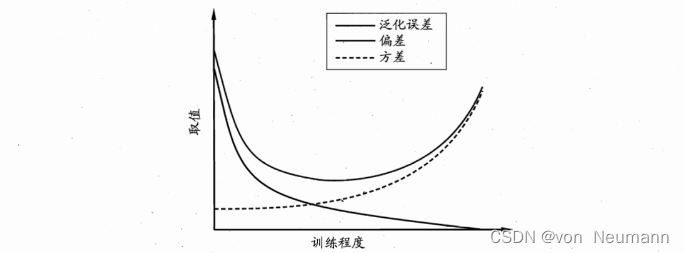
深入理解机器学习——偏差(Bias)与方差(Variance)
分类目录:《深入理解机器学习》总目录 偏差(Bias)与方差(Variance)是解释学习算法泛化性能的一种重要工具。偏差方差分解试图对学习算法的期望泛化错误率进行拆解,我们知道,算法在不同训练集上学…...

分布式新闻项目实战 - 13.项目部署_持续集成(Jenkins) ^_^ 完结啦 ~
欲买桂花同载酒,终不似,少年游。 系列文章目录 项目搭建App登录及网关App文章自媒体平台(博主后台)自媒体文章审核延迟任务kafka及文章上下架App端文章搜索后台系统管理Long类型精度丢失问题定时计算热点文章(xxl-Job…...

Linux c/c++技术方向分析
一、C与C介绍 1.1 说明 c语言是一门面向过程的、抽象化的通用程序设计语言,广泛应用于底层开发,如嵌入式。C语言能以简易的方式编译、处理低级存储器。是一种高效率程序设计语言。 c(c plus plus)是一种计算机高级程序设计语言&a…...
JavaScript 高级3 :函数进阶
JavaScript 高级3 :函数进阶 Date: January 19, 2023 Text: 函数的定义和调用、this、严格模式、高阶函数、闭包、递归 目标: 能够说出函数的多种定义和调用方式 能够说出和改变函数内部 this 的指向 能够说出严格模式的特点 能够把函数作为参数和返…...
【项目】Java树形结构集合分页,java对list集合进行分页
Java树形结构集合分页需求难点实现第一步:查出所有树形集合数据 (需进行缓存处理)selectTree 方法步骤:TreeUtil类:第二步:分页 GoodsCategoryController分页getGoodsCategoryTree方法步骤:第三…...
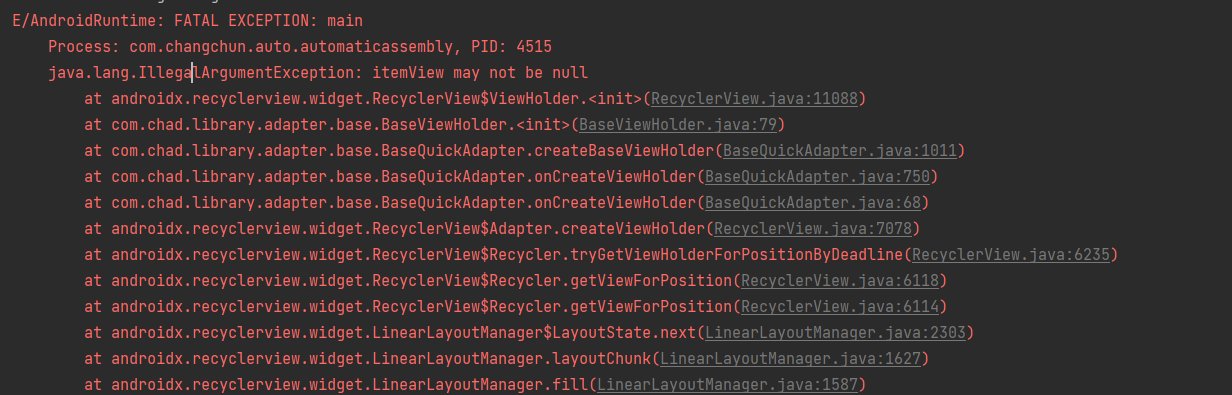
java.lang.IllegalArgumentException: itemView may not be null
报错截图:场景介绍:在使用recycleView 自动递增数据,且自动滚动到最新行; 当数据达到273条 时出现ANR;项目中 全部的列表适配器使用的三方库:BaseRecyclerViewAdapterHelper (很早之前的项目&am…...
[ 攻防演练演示篇 ] 利用 shiro 反序列化漏洞获取主机权限
🍬 博主介绍 👨🎓 博主介绍:大家好,我是 _PowerShell ,很高兴认识大家~ ✨主攻领域:【渗透领域】【数据通信】 【通讯安全】 【web安全】【面试分析】 🎉点赞➕评论➕收藏 养成习…...

达人合作加持品牌布局,3.8女神玩转流量策略!
随着迅猛发展的“她经济”,使社区本就作为内容种草的平台,自带“营销基因”。在3.8女神节即将到来之际,如何充分利用平台女性资源优势,借助达人合作等手段,实现迅速引流,来为大家详细解读下。一、小红书节日…...
观点丨Fortinet谈ChatGPT火爆引发的网络安全行业剧变
FortiGuard报告安全趋势明确指出“网络攻击者已经开始尝试AI手段”,ChatGPT的火爆之际的猜测、探索和事实正在成为这一论断的佐证。攻守之道在AI元素的加持下也在悄然发生剧变。Fortinet认为在攻击者利用ChatGPT等AI手段进行攻击的无数可能性的本质,其实…...

工业企业用电损耗和降损措施研究
来自用电设备和供配电系统的电能损耗。而供配电系统的电能损耗,包括企业变配电设备、控制设备企业在不断降低生产成本,追求经济效益的情况下,进一步降低供配电系统中的电能损耗,使电气设摘要:电网电能损耗是一个涉及面很广的综合性问题,主要包括管理损耗和技术损耗两部分…...

高并发、高性能、高可用
文章目录一、高并发是什么?二、 高性能是什么三、 高可用什么是一、高并发是什么? 示例:高并发是现在互联网分布式框架设计必须要考虑的因素之一,它是可以保证系统能被同时并行处理很多请求,对于高并发来说࿰…...
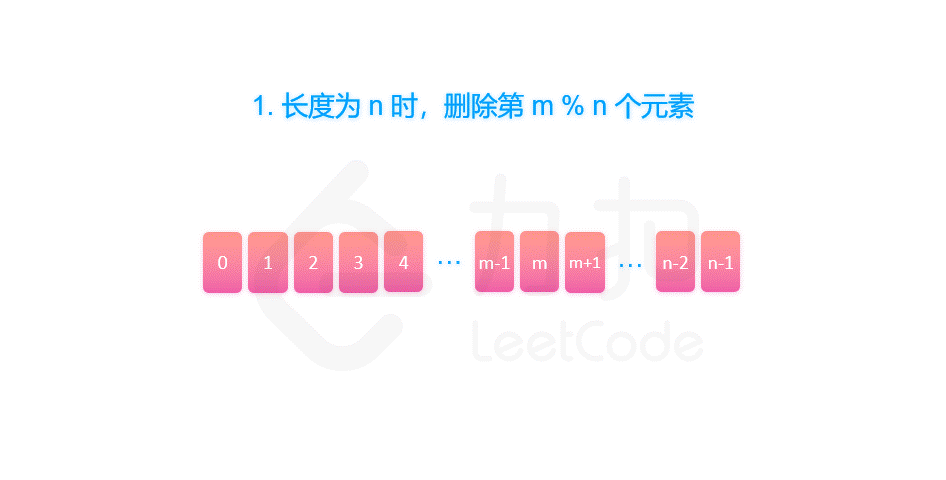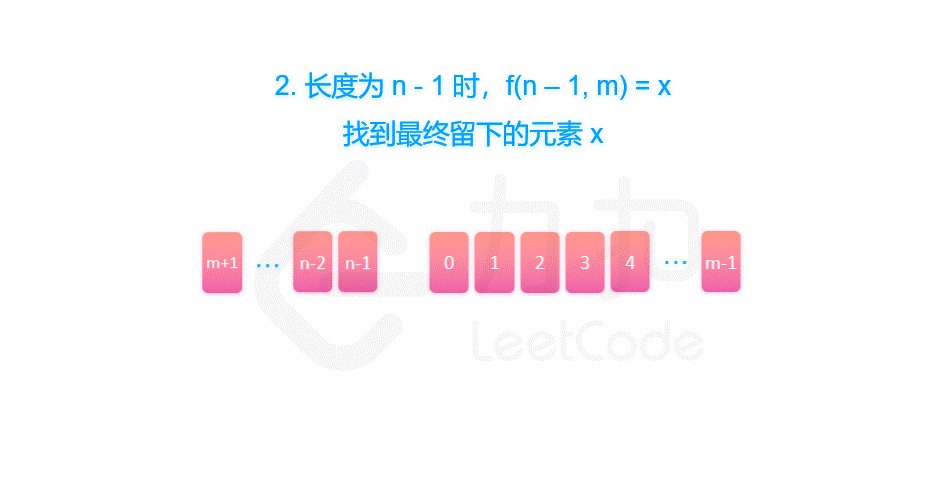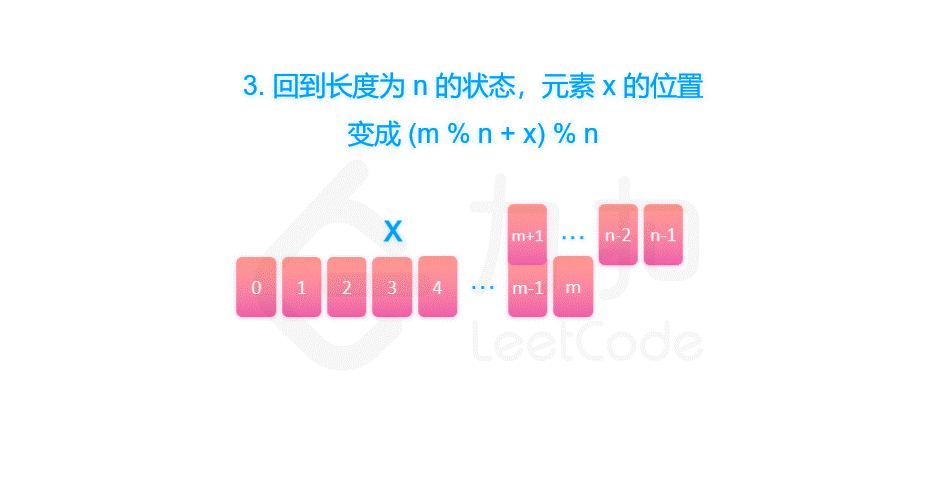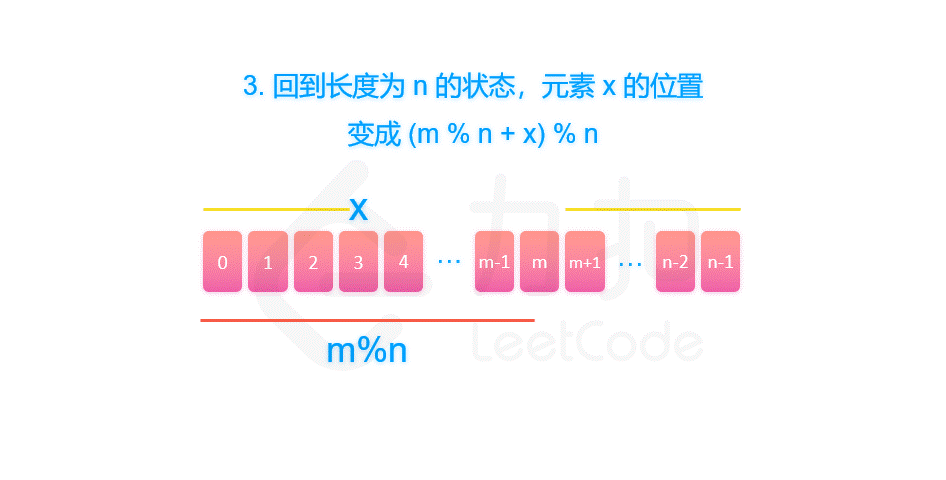
剑指 Offer 62. 圆圈中最后剩下的数字
摘要 剑指 Offer 62. 圆圈中最后剩下的数字 一、约瑟夫环解析 题目中的要求可以表述为:给定一个长度为 n 的序列,每次向后数 m 个元素并删除,那么最终留下的是第几个元素?这个问题很难快速给出答案。但是同时也要看到ÿ…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...
