【C++算法竞赛 · 图论】图论基础
前言
图论基础
图的相关概念
图的定义
图的分类
按数量分类:
按边的类型分类:
边权
简单图
度
路径
连通
无向图
有向图
图的存储
方法概述
代码
复杂度
前言
图论(Graph theory),是 OI 中的一样很大的一个模块,围绕它有很多高难度的算法以及高级的概念。这篇文章将介绍关于图论的一部分基础概念(干货满满!),话不多说,步入正题——
图论基础
(干货太多了,建议先收藏!)
图的相关概念
图的定义
图(graph)是一个二元组 G = (V(G), E(G))。其中 V(G) 是非空集,称为 点集(vertex set),对于 V 中的每个元素,我们称其为 顶点(vertex)或 节点(node),简称 点;E(G) 为 V(G) 各结点之间边的集合,称为 边集(edge set)。
我们一般用 G = (V, E) 表示图。
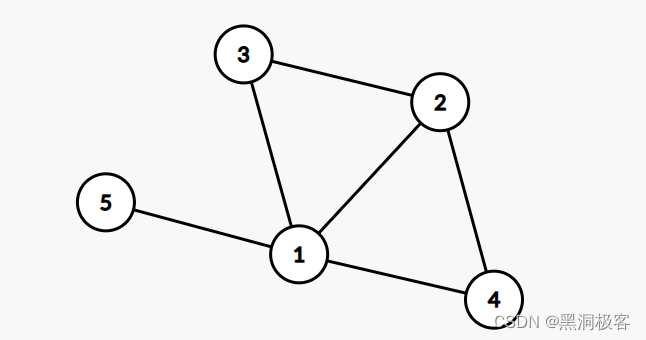
举个例子:
这就是一张图,1,2,3,4,5 就是它的节点。
推荐一个网站:Cs Academy
这里有十分好用的图编辑器,可以帮你加强理解图论!
图的分类
按数量分类:
当 V, E 都是有限集合时,称 G 为 有限图。
当 V 或 E 是无限集合时,称 G 为 无限图。
按边的类型分类:
图有多种,包括 无向图 (undirected graph),有向图 (directed graph),混合图 (mixed graph) 等。
若为无向图,则图中的每个元素为一个无序二元组 (u, v),称作 无向边 (undirected edge),简称 边 (edge),其中 u, v ∈ V。设 e = (u, v),则 u 和 v 称为 e 的 端点 (endpoint)。
若为有向图,则图中的每一个元素为一个有序二元组 (u, v),有时也写作 u → v,称作 有向边 (directed edge) 或 弧 (arc),在不引起混淆的情况下也可以称作 边 (edge)。设 e = u → v ,则此时 u 称为 e 的 起点 (tail),v 称为 e 的 终点 (head),起点和终点也称为 e 的 端点 (endpoint)。并称 u 是 v 的直接前驱,v 是 u 的直接后继。
若为混合图,则图中既有 有向边,又有 无向边。
还拿这张图来说,这是一个无向图。
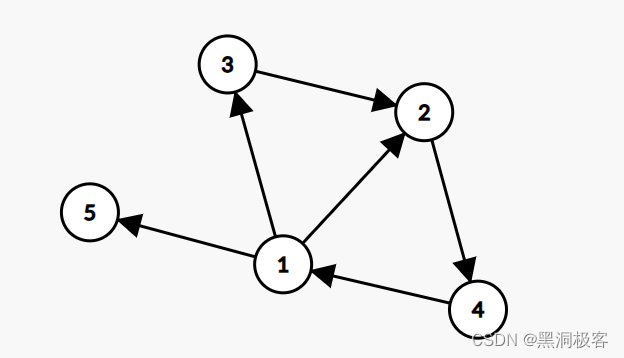
这就是一张有向图。
边权
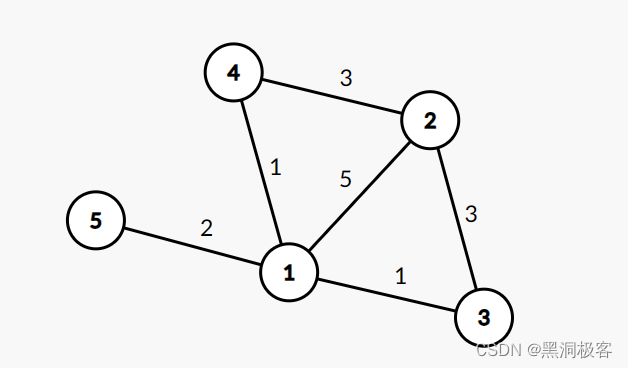
若图的每条边都被赋予一个数作为该边的 权,则称这张图为 赋权图。如果这些权都是正实数,就称为 正权图。
这张图就是一张 赋权图。
简单图
自环 (loop):对 E 中的边 e = (u,v) ,若 u = v ,则 e 被称作一个自环。
重边 (multiple edge):若 E 中存在两个完全相同的元素(边)e1,e2 ,则它们被称作(一组)重边。
简单图 (simple graph):若一个图中没有自环和重边,它被称为简单图。具有至少两个顶点的简单无向图中一定存在度相同的结点。
如果一张图中有自环或重边,则称它为 多重图 (multigraph)。
度
与一个顶点 v 关联的边的条数称作该顶点的 度 (degree),记作 d(v)。特别地,对于边 (v, v),则每条这样的边要对 d(v) 产生 2 的贡献。
对于无向简单图,有 d(v) = |N(v)|。
推论:在任意图中,度数为奇数的点必然有偶数个。(一笔画问题应该了解过吧)
若 d(v) = 0,则称 v 为 孤立点 (isolated vertex)。
若 d(v) = 1,则称 v 为 叶节点 (leaf vertex)/悬挂点 (pendant vertex)。
若 2 | d(v),则称 v 为 偶点 (even vertex),否则为 奇点 (odd vertex)。
若 d(v) = |V| - 1,则称 v 为 支配点 (universal vertex)。
(这些概念了解就行了,不需要特别去记)
对一张图,所有节点的度数的最小值称为 最小度 (minimum degree),最大值称为 最大度 (maximum degree)。
在有向图中,以一个顶点为起点的边的条数称为该顶点的 出度 (out-degree),以一个顶点 ![]() 为终点的边的条数称为该节点的 入度 (in-degree)。
为终点的边的条数称为该节点的 入度 (in-degree)。
如果给定一个序列 a,可以找到一个图 G,以其为度数列,则称 a 是 可图化 的。
如果给定一个序列 a,可以找到一个简单图 G,以其为度数列,则称 a 是 可简单图化 的。
路径
途径 (walk):途径是连接一连串顶点的边的序列,可以为有限或无限长度。形式化地说,一条有限途径 w 是一个边的序列 e1,e2,...,ek,使得存在一个顶点序列 v0,v1,...,vk 满足 ei = (v i-1,v i),其中 i ∈ [1, k] 。这样的途径可以简写为 v0 → v1 → v2 → ... → vk 。通常来说,边的数量 k 被称作这条途径的 长度(如果边是带权的,长度通常指途径上的边权之和,题目中也可能另有定义)。
看不懂?
(我也看不懂)为了更好地理解,可以把一张图当作一个地图,节点就是车站,边就是路,那么路径就是从一个车站到另一个车站的路线。如果这张图是赋权图,也就是说车站之间有了距离,那么路径的 长度 就是车站到车站的路线的长度。
回路 (circuit):对于一条路径 w![]() ,若 v0 = vk,则称 w 是一条回路。
,若 v0 = vk,则称 w 是一条回路。
连通
无向图
对于一张无向图 G = (V,E),对于 u,v ∈ V,若存在一条途径使得 v0 = u, vk = v,则称 u 和 v 是 连通的 (connected)。由定义,任意一个顶点和自身连通,任意一条边的两个端点连通。
若无向图 G = (V,E),满足其中任意两个顶点均连通,则称 G 是 连通图 (connected graph),这一性质称作 连通性 (connectivity)。
有向图
对于一张有向图 G = (V,E),对于 u,v ∈ V,若存在一条途径使得 v0 = u, vk = v, 则称 u 可达 v。由定义,任意一个顶点可达自身,任意一条边的起点可达终点。(无向图中的连通也可以视作双向可达。)
若一张有向图的节点两两互相可达,则称这张图是 强连通的 (strongly connected)。
若一张有向图的边替换为无向边后可以得到一张连通图,则称原来这张有向图是 弱连通的 (weakly connected)。
到这,你已经看过了图的大部分概念。全是干货,如果还没理解,可以收藏起来慢慢看!
图的存储
本文会介绍最常用的存储方法,也就是:直接存边。
方法概述
使用一个数组来存边,数组中的每个元素都包含一条边的起点与终点(带边权的图还包含边权)。
代码
struct Edge {int u, v;
};
vector<Edge> e;复杂度
查询是否存在某条边:O(m) 。
遍历一个点的所有出边:O(m) 。
遍历整张图:O(nm) 。
空间复杂度:O(m) 。
干货太多,整理得肝疼,求个点赞收藏不过分吧!(求求了!)
本文就到这里,下次再见!
相关文章:

【C++算法竞赛 · 图论】图论基础
前言 图论基础 图的相关概念 图的定义 图的分类 按数量分类: 按边的类型分类: 边权 简单图 度 路径 连通 无向图 有向图 图的存储 方法概述 代码 复杂度 前言 图论(Graph theory),是 OI 中的一样很大…...
Java解析实体类的属性和属性注释
前言 获取某个类的属性(字段)是我们经常都会碰到的,通常我们是通过反射来获取的。 但是有些特殊情况下,我们不仅要获取类的属性,还需要获取属性注释。这种情况下,我们只能通过注解去获取注释。可以自己定…...
机器学习KNN最邻近分类算法
文章目录 1、KNN算法简介2、KNN算法实现2.1、调用scikit-learn库中KNN算法 3、使用scikit-learn库生成数据集3.1、自定义函数划分数据集3.2、使用scikit-learn库划分数据集 4、使用scikit-learn库对鸢尾花数据集进行分类5、什么是超参数5.1、实现寻找超参数5.2、使用scikit-lea…...
)
分享一个Python爬虫入门实例(有源码,学习使用)
一、爬虫基础知识 Python爬虫是一种使用Python编程语言实现的自动化获取网页数据的技术。它广泛应用于数据采集、数据分析、网络监测等领域。以下是对Python爬虫的详细介绍: 架构和组成:下载器:负责根据指定的URL下载网页内容,常用的库有Requests和urllib。解析器:用于解…...
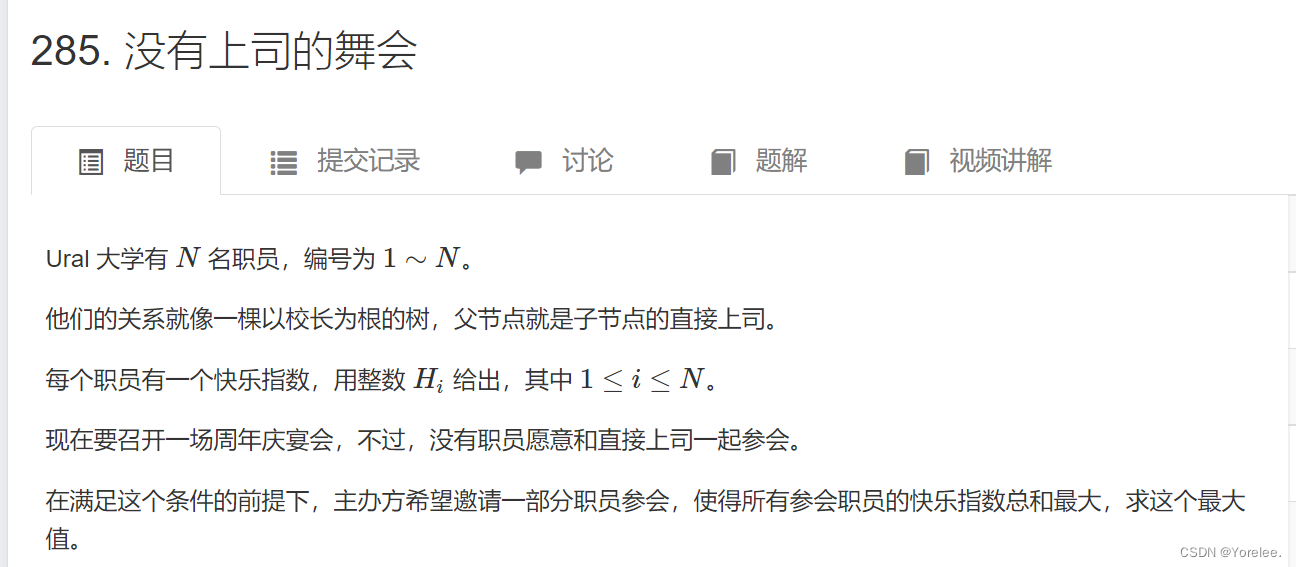
算法:树形dp(树状dp)
文章目录 一、树形DP的概念1.基本概念2.解题步骤3.树形DP数据结构 二、典型例题1.LeetCode:337. 打家劫舍 III1.1、定义状态转移方程1.2、参考代码 2.ACWing:285. 没有上司的舞会1.1、定义状态转移方程1.2、拓扑排序参考代码1.3、dfs后序遍历参考代码 一…...
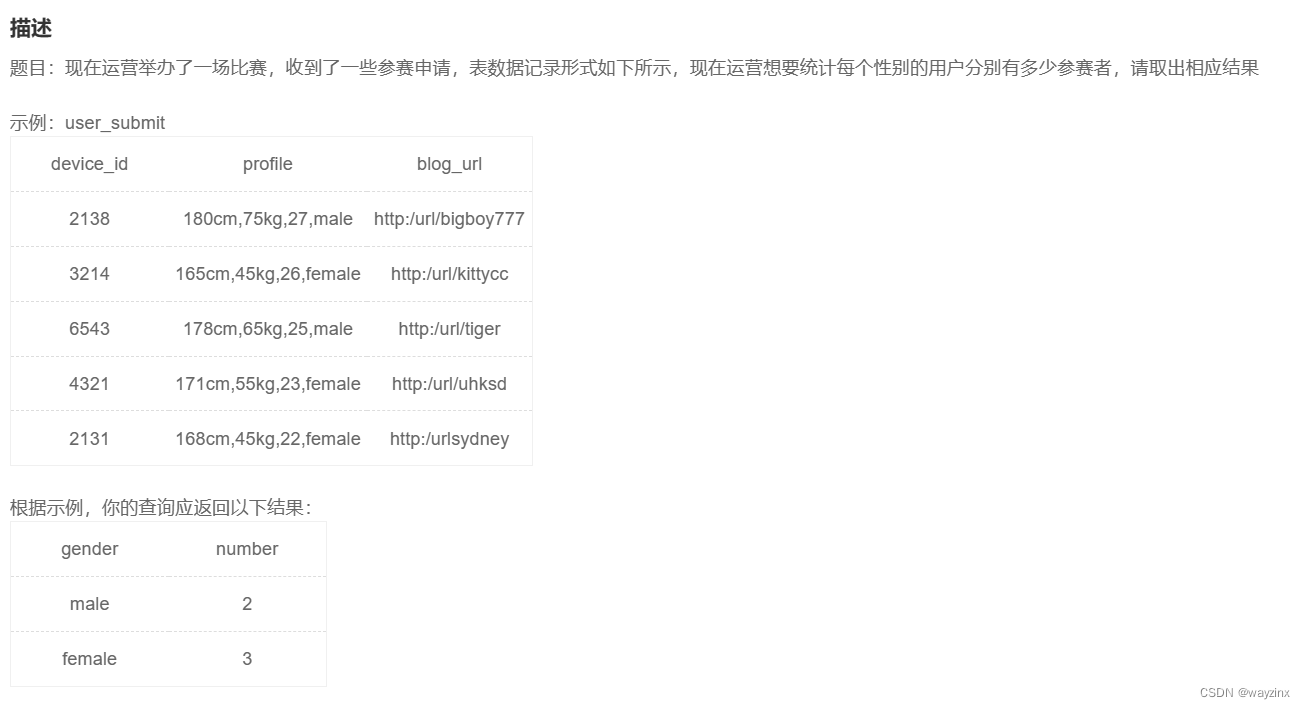
SQL语句学习+牛客基础39SQL
什么是SQL? SQL (Structured Query Language:结构化查询语言) 是用于管理关系数据库管理系统(RDBMS)。 SQL 的范围包括数据插入、查询、更新和删除,数据库模式创建和修改,以及数据访问控制。 SQL语法 数据库表 一个…...
动态规划)
竞赛常考的知识点大总结(五)动态规划
DP问题的性质 动态规划(Dynamic Programming,DP)是指在解决动态规划问题时所依赖的一些基本特征和规律。动态规划是一种将复杂问题分解为更小子问题来解决的方法,它适用于具有重叠子问题和最优子结构性质的问题。动态规划问题通常…...
如何在 Mac 上恢复已删除的数据
如果您丢失了 Mac 上的数据,请不要绝望。恢复数据比您想象的要容易,并且有很多方法可以尝试。 在 Mac 上遭受数据丢失是每个人都认为永远不会发生在他们身上的事情之一......直到它发生。不过,请不要担心,因为您可以通过多种方法…...

Java笔试题总结
HashSet子类依靠()方法区分重复元素。 A toString(),equals() B clone(),equals() C hashCode(),equals() D getClass(),clone() 答案:C 解析: 先调用对象的hashcode方法将对象映射为数组下标,再通过equals来判断元素内容是否相同 以下程序执行的结果是: class X{…...
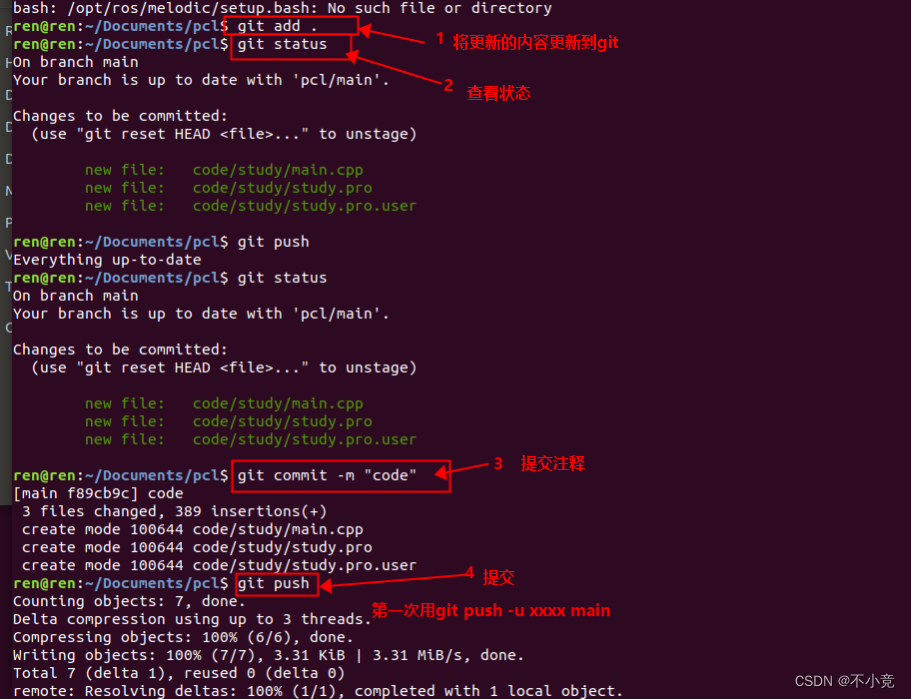
github本地仓库push到远程仓库
1.从远程仓库clone到本地 2.生成SSH秘钥,为push做准备 在Ubuntu命令行输入一下内容 [rootlocalhost ~]# ssh-keygen -t rsa < 建立密钥对,-t代表类型,有RSA和DSA两种 Generating public/private rsa key pair. Enter file in whi…...

Error: TF_DENORMALIZED_QUATERNION: Ignoring transform forchild_frame_id
问题 运行程序出现: Error: TF_DENORMALIZED_QUATERNION: Ignoring transform for child_frame_id “odom” from authority “unknown_publisher” because of an invalid quaternion in the transform (0.0 0.0 0.0 0.707) 主要是四元数没有归一化 Eigen::Quatern…...

Linux从入门到精通 --- 2.基本命令入门
文章目录 第二章:2.1 Linux的目录结构2.1.1 路径描述方式 2.2 Linux命令入门2.2.1 Linux命令基础格式2.2.2 ls命令2.2.3 ls命令的参数和选项2.2.4 ls命令选项的组合使用 2.3 目录切换相关命令2.3.1 cd切换工作目录2.3.2 pwd查看当前工作目录2.4 相对路径、绝对路径和…...
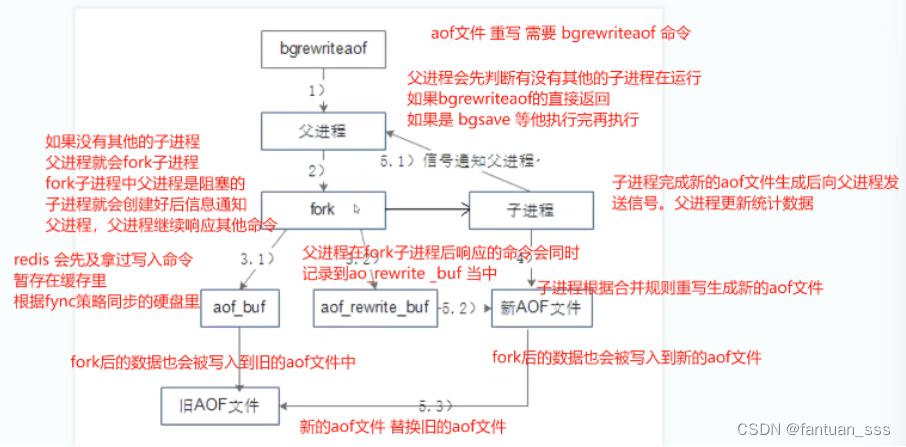
Redis常用命令补充和持久化
一、redis 多数据库常用命令 1.1 多数据库间切换 1.2 多数据库间移动数据 1.3 清除数据库内数据 1.4 设置密码 1.4.1 使用config set requirepass yourpassword命令设置密码 1.4.2 使用config get requirepass命令查看密码 二、redis高可用 2.1 redis 持久化 2.1.1 持…...
二次开发时的错误码)
【记录】海康相机(SDK)二次开发时的错误码
海康相机(SDK)二次开发时的错误码 在进行海康sdk二次开发的时候,经常碰到各种错误,遂结合官方文档和广大网友的一些经验,把这些错误码记录一下,方便查找。笔者使用的SDK版本是HCNetSDKV6.1.9.4。 错误类型…...

端盒日记Day02
JS 本本本本本地存储 localStorage 作用:可以将数据永久存储在本地(用户电脑),除非手动删除,否则关闭页面也会存在 特性:a.可多窗口(页面)共享(同一浏览器可以共享&a…...

考研高数(平面图形的面积,旋转体的体积)
1.平面图形的面积 纠正:参数方程求面积 2.旋转体的体积(做题时,若以x为自变量不好计算,可以求反函数,y为自变量进行计算)...

选择企业邮箱,扬帆迈向商务新纪元!
企业邮箱和个人邮箱不同,它的邮箱后缀是企业自己的域名。企业邮箱供应商一般都提供手机app、桌面端、web浏览器访问等邮箱使用途径。那么什么是企业邮箱?如何选择合适的企业邮箱?好用的企业邮箱应具备无缝迁移、协作、多邮箱管理等功能。 企…...

2024.3.25力扣每日一题——零钱兑换2
2024.3.25 题目来源我的题解方法一 动态规划 题目来源 力扣每日一题;题序:518 我的题解 方法一 动态规划 给定总金额 amount 和数组 coins,要求计算金额之和等于 amount 的硬币组合数。其中,coins的每个元素可以选取多次&#…...

包子凑数【蓝桥杯】/完全背包
包子凑数 完全背包 完全背包问题和01背包的区别就是,完全背包问题每一个物品能取无限次。 思路:当n个数的最大公约数不为1,即不互质时,有无限多个凑不出来的,即n个数都可以表示成kn,k为常数且不为1。当n个…...

口语 4.6
drop the gun :逃避 radically 极大程度地 vastly cognition:认知能力 flaw缺陷 flawless:没有缺陷 interface:接口,交流处 retain:保留 down the rabbit hole:进入未知领域了 wrap your head aro…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...
实现跳一跳小游戏)
鸿蒙(HarmonyOS5)实现跳一跳小游戏
下面我将介绍如何使用鸿蒙的ArkUI框架,实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...

Python 高级应用10:在python 大型项目中 FastAPI 和 Django 的相互配合
无论是python,或者java 的大型项目中,都会涉及到 自身平台微服务之间的相互调用,以及和第三发平台的 接口对接,那在python 中是怎么实现的呢? 在 Python Web 开发中,FastAPI 和 Django 是两个重要但定位不…...

【深尚想】TPS54618CQRTERQ1汽车级同步降压转换器电源芯片全面解析
1. 元器件定义与技术特点 TPS54618CQRTERQ1 是德州仪器(TI)推出的一款 汽车级同步降压转换器(DC-DC开关稳压器),属于高性能电源管理芯片。核心特性包括: 输入电压范围:2.95V–6V,输…...