matlab:五点中心差分求解Navier边界的Biharmonic方程(具有纳维尔边界的双调和方程)
我们考虑如下形式的双调和方程的数值解
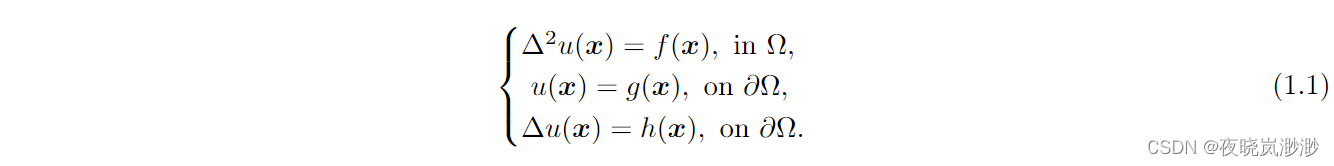
其中,Ω是欧氏空间中的多边形或多面体域,在其中,d为维度,具有分段利普希茨边界,满足内部锥条件,f(x) ∈ L2(Ω)是给定的函数,∆是标准的拉普拉斯算子。算子∆u(x)和∆2u(x)表示为
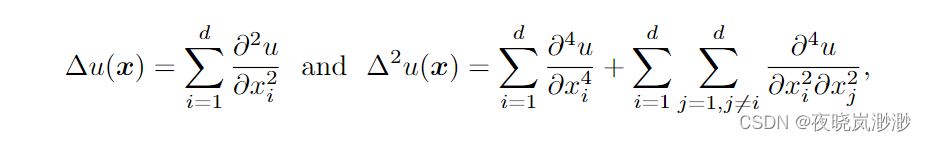
巧妙地将双调和方程(1.1)分解为两个Possion方程,传统的数值方法如有限元法(FEM)和有限差分法(FDM)在计算资源和时间复杂度较小的情况下表现良好。通过引入辅助变量w = −∆u,可以将四阶方程(1.1)重写为一对二阶方程:
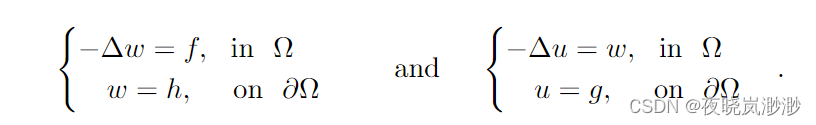
或者引入变量w = ∆u,得到
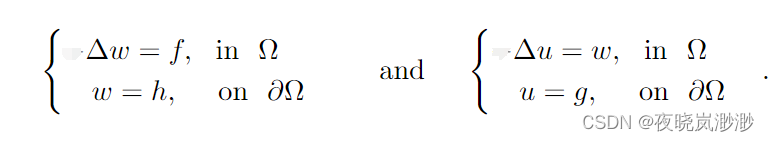
那么,我们的目标为寻找一对函数(w,u),而不是找到原始问题(1.1)的解。如下我们以g=0和h=0为例,利用五点中心差分求解上面的双调和方程。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%% Matrix method for Biharmonic Equation %%%%
%%% u_{xxxx} + u_{yyyy} + 2*u_{xx}*u_{yy} = f(x, y) %%%%
%%% Omega = 0 < x < 1, 0 < y < 1 %%%%
%%% u(x, y) = 0 on boundary, %%%%
%%% Exact soln: u(x, y) = sin(pi*x)*sin(pi*y) %%%%
%%% Here f(x, y) = 4*pi^4*sin(pi*x)*sin(pi*y); %%%%
%%% Course: Xi'an Li on 12.08 2023 %%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%clear all
clc
close allftsz = 20;x_l = -1.0;
x_r = 1.0;
y_b = -1.0;
y_t = 1.0;q = 6;
Num = 2^q+1;
NNN = Num*Num;point_num2x = Num;
point_num2y = Num;fside = @(x, y) 4*pi^4*sin(pi*x).*sin(pi*y);
utrue = @(x, y) sin(pi*x).*sin(pi*y);hx = (x_r-x_l)/point_num2x;
X = zeros(point_num2x-1,1);
for i=1:point_num2x-1X(i) = x_l+i*hx;
endhy = (y_t-y_b)/point_num2y;
Y=zeros(point_num2y-1,1);
for i=1:point_num2y-1Y(i) = y_b+i*hy;
end
[meshX, meshY] = meshgrid(X, Y);tic;
Unumberi = FDM2Biharmonic_Couple2Navier_Zero(point_num2x, point_num2y,...x_l, x_r, y_b, y_t, fside);
fprintf('%s%s%s\n','运行时间:',toc,'s')
U_exact = utrue(meshX, meshY);
meshErr = abs(U_exact - Unumberi);rel_err = sum(sum(meshErr))/sum(sum(abs(U_exact)));
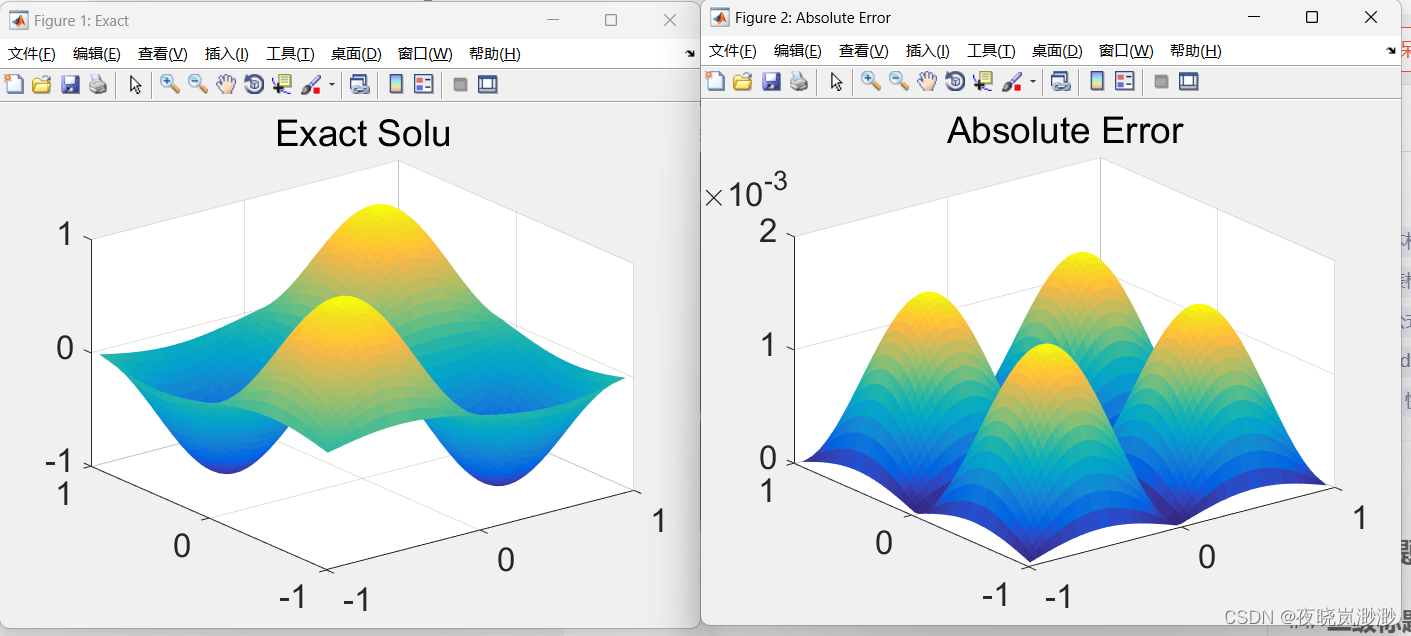
fprintf('%s%s\n','相对误差:',rel_err)figure('name','Exact')
axis tight;
h = surf(meshX, meshY, U_exact','Edgecolor', 'none');
hold on
title('Exact Solu')
% xlabel('$x$', 'Fontsize', 20, 'Interpreter', 'latex')
% ylabel('$y$', 'Fontsize', 20, 'Interpreter', 'latex')
% zlabel('$Error$', 'Fontsize', 20, 'Interpreter', 'latex')
hold on
set(gca, 'XMinortick', 'off', 'YMinorTick', 'off', 'Fontsize', ftsz);
set(gcf, 'Renderer', 'zbuffer');
hold on
% colorbar;
% caxis([0 0.00012])
hold onfigure('name','Absolute Error')
axis tight;
h = surf(meshX, meshY, meshErr','Edgecolor', 'none');
hold on
title('Absolute Error')
% xlabel('$x$', 'Fontsize', 20, 'Interpreter', 'latex')
% ylabel('$y$', 'Fontsize', 20, 'Interpreter', 'latex')
% zlabel('$Error$', 'Fontsize', 20, 'Interpreter', 'latex')
hold on
set(gca, 'XMinortick', 'off', 'YMinorTick', 'off', 'Fontsize', ftsz);
set(gcf, 'Renderer', 'zbuffer');
hold on
% colorbar;
% caxis([0 0.00012])
hold onif q==6txt2result = 'result2fdm_mesh6.txt';
elseif q==7txt2result = 'result2fdm_mesh7.txt';
elseif q==8txt2result = 'result2fdm_mesh8.txt';
elseif q==9txt2result = 'result2fdm_mesh9.txt';
endfop = fopen(txt2result, 'wt');fprintf(fop,'%s%s%s\n','运行时间:',toc,'s');
fprintf(fop,'%s%d\n','内部网格点数目:',Num-1);
fprintf(fop,'%s%s\n','相对误差:',rel_err);
被调用的求解函数如下:
function Uapp = FDM2Biharmonic_Couple2Navier_Zero(Nx, Ny, xleft, xright, ybottom, ytop, fside)format long;% Define the step sizes and create the grid without boundary pointshx = (xright-xleft)/Nx; x = zeros(Nx-1,1);for ix=1:Nx-1x(ix) = xleft+ix*hx;endhy = (ytop-ybottom)/Ny; y=zeros(Ny-1,1);for iy=1:Ny-1y(iy) = ybottom+iy*hy;end% Define the source termsource_term = fside;% Initialize the coefficient matrix A and the right-hand side vector FN = (Ny-1)*(Nx-1);A = sparse(N,N); FV = zeros(N,1);% Loop through each inner grid point, Apply finite difference scheme (central differences)hx1 = hx*hx; hy1 = hy*hy; for jv = 1:Ny-1for iv=1:Nx-1kv = iv + (jv-1)*(Nx-1);FV(kv) = fside(x(iv),y(jv));A(kv,kv) = -2/hx1 -2/hy1;%-- x direction --------------if iv == 1A(kv,kv+1) = 1/hx1;elseif iv==Nx-1A(kv,kv-1) = 1/hx1;elseA(kv,kv-1) = 1/hx1;A(kv,kv+1) = 1/hx1;endend%-- y direction --------------if jv == 1A(kv,kv+Nx-1) = 1/hy1;elseif jv==Ny-1A(kv,kv-(Nx-1)) = 1/hy1;elseA(kv,kv-(Nx-1)) = 1/hy1;A(kv,kv+Nx-1) = 1/hy1;endendendendV = A\FV;B = sparse(N,N); FU = zeros(N,1);% Loop through each inner grid point, Apply finite difference scheme (central differences)for ju = 1:Ny-1for iu=1:Nx-1ku = iu + (ju-1)*(Nx-1);FV(ku) = V(ku);B(ku,ku) = -2/hx1 -2/hy1;%-- x direction --------------if iu == 1B(ku,ku+1) = 1/hx1;elseif iu==Nx-1B(ku,ku-1) = 1/hx1;elseB(ku,ku-1) = 1/hx1;B(ku,ku+1) = 1/hx1;endend%-- y direction --------------if ju == 1B(ku,ku+Nx-1) = 1/hy1;elseif ju==Ny-1B(ku,ku-(Nx-1)) = 1/hy1;elseB(ku,ku-(Nx-1)) = 1/hy1;B(ku,ku+Nx-1) = 1/hy1;endendendendU = B\FV;%--- Transform back to (i,j) form to plot the solution ---j = 1;for k=1:Ni = k - (j-1)*(Nx-1) ;Uapp(i,j) = U(k);j = fix(k/(Nx-1)) + 1;end
end
结果如下:
运行时间:6.574370e-02s
相对误差:1.558669e-03
相关文章:

matlab:五点中心差分求解Navier边界的Biharmonic方程(具有纳维尔边界的双调和方程)
我们考虑如下形式的双调和方程的数值解 其中,Ω是欧氏空间中的多边形或多面体域,在其中,d为维度,具有分段利普希茨边界,满足内部锥条件,f(x) ∈ L2(Ω)是给定的函数,∆是标准的拉普拉斯算子。算…...
详细介绍微信小程序app.js
这一节,我们详细介绍app.js 这个文件。这个文件的重要性我就不再赘述,前面已经介绍了。 一、app.js是项目的主控文件 任何一个程序都是需要一个入口的,就好比我们在学c的时候就会有一个main函数,其他语言基本都是一样。很明确的…...

【六 (2)机器学习-EDA探索性数据分析模板】
目录 文章导航一、EDA:二、导入类库三、导入数据四、查看数据类型和缺失情况五、确认目标变量和ID六、查看目标变量分布情况七、特征变量按照数据类型分成定量变量和定性变量八、查看定量变量分布情况九、查看定量变量的离散程度十、查看定量变量与目标变量关系十一…...
Java集合——Map、Set和List总结
文章目录 一、Collection二、Map、Set、List的不同三、List1、ArrayList2、LinkedList 四、Map1、HashMap2、LinkedHashMap3、TreeMap 五、Set 一、Collection Collection 的常用方法 public boolean add(E e):把给定的对象添加到当前集合中 。public void clear(…...

Python TensorFlow 2.6 获取 MNIST 数据
Python TensorFlow 2.6 获取 MNIST 数据 2 Python TensorFlow 2.6 获取 MNIST 数据1.1 获取 MNIST 数据1.2 检查 MNIST 数据 2 Python 将npz数据保存为txt3 Java 获取数据并使用SVM训练4 Python 测试SVM准确度 2 Python TensorFlow 2.6 获取 MNIST 数据 1.1 获取 MNIST 数据 …...

EChart简单入门
echart的安装就细不讲了,直接去官网下,实在不会的直接用cdn,省的一番口舌。 cdn.staticfile.net/echarts/4.3.0/echarts.min.js 正入话题哈 什么是EChart? EChart 是一个使用 JavaScript 实现的开源可视化库,Echart支持多种常…...
阿里云8核32G云服务器租用优惠价格表,包括腾讯云和京东云
8核32G云服务器租用优惠价格表,云服务器吧yunfuwuqiba.com整理阿里云8核32G服务器、腾讯云8核32G和京东云8C32G云主机配置报价,腾讯云和京东云是轻量应用服务器,阿里云是云服务器ECS: 阿里云8核32G服务器 阿里云8核32G服务器价格…...

设计模式,工厂方法模式
工厂方法模式概述 工厂方法模式,是对简单工厂模式的进一步抽象和推广。以我个人理解,工厂方法模式就是对生产工厂的抽象,就是用一个生产工厂的工厂来进行目标对象的创建。 工厂方法模式的角色组成和简单工厂方法相比,创建了一个…...

WPF中嵌入3D模型通用结构
背景:wpf本身有提供3D的绘制,但是自己通过代码描绘出3D是比较困难的。3D库helix-toolkit支持调用第三方生成的模型,比如Blender这些,所以在wpf上使用3D就变得非常简单。这里是一个通过helix-toolkit库调用第三方生成的3d模型的样例…...

举个例子说明联邦学习
学习目标: 一周掌握 Java 入门知识 学习内容: 联邦学习是一种机器学习方法,它允许多个参与者协同训练一个共享模型,同时保持各自数据的隐私。 联邦学习概念(例子): 假设有三家医院,它们都希望…...

【Python】免费的图片/图标网站
专栏文章索引:Python 有问题可私聊:QQ:3375119339 这里是我收集的几个免费的图片/图标网站: iconfont-阿里巴巴矢量图标库icon(.ico)INCONFINDER(.ico)...
)
Pytorch中的nn.Embedding()
模块的输入是一个索引列表,输出是相应的词嵌入。 Embedding.weight(Tensor)–形状模块(num_embeddings,Embedding_dim)的可学习权重,初始化自(0,1)。 也就是…...

WebSocketServer后端配置,精简版
首先需要maven配置 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId><version>2.1.3.RELEASE</version></dependency> 然后加上配置类 这段代码是一个Spri…...

Python程序设计 多重循环(二)
1.打印数字图形 输入n(n<9),输出由数字组成的直角三角图形。例如,输入5,输出图形如下 nint(input("")) #开始 for i in range(1,n1):for j in range(1,i1):print(j,end"")print()#结束 2.打印字符图形 …...
)
前端面试题--CSS系列(一)
CSS系列--持续更新中 1.CSS预处理器有哪些类型,有什么区别2.盒模型是什么,有哪两种类型3.css选择器有哪些,优先级是怎样的,哪些属性可以继承4. 说说em/px/rem/vh/vw的区别5.元素实现水平垂直居中的方法有哪些,如果元素…...
VSCode好用插件
由于现在还是使用vue2,所以本文只记录vue2开发中好用的插件。 美化类插件不介绍了,那些貌似对生产力起不到什么大的帮助,纯粹的“唯心主义”罢了,但是如果你有兴趣的话可以查看上一篇博客:VSCode美化 1. vuter 简介&…...

Vue3:对ref、reactive的一个性能优化API
一、情景说明 我们知道,在Vue3中,想要创建响应式的变量,就要用到ref、reactive来包裹一下数据即可。 但是,这里有个损耗性能的地方 就是,被它包裹的数据,都会构建成响应式的,无论多少层次&…...
Python 用pygame简简单单实现一个打砖块
# -*- coding: utf-8 -*- # # # Copyright (C) 2024 , Inc. All Rights Reserved # # # Time : 2024/3/30 14:34 # Author : 赫凯 # Email : hekaiiii163.com # File : ballgame.py # Software: PyCharm import math import randomimport pygame import sys#…...

软考113-上午题-【计算机网络】-IPv6、无线网络、Windows命令
一、IPv6 IPv6 具有长达 128 位的地址空间,可以彻底解决 IPv4 地址不足的问题。由于 IPv4 地址是32 位二进制,所能表示的IP 地址个数为 2^32 4 294 967 29640 亿,因而在因特网上约有 40亿个P 地址。 由 32 位的IPv4 升级至 128 位的IPv6&am…...
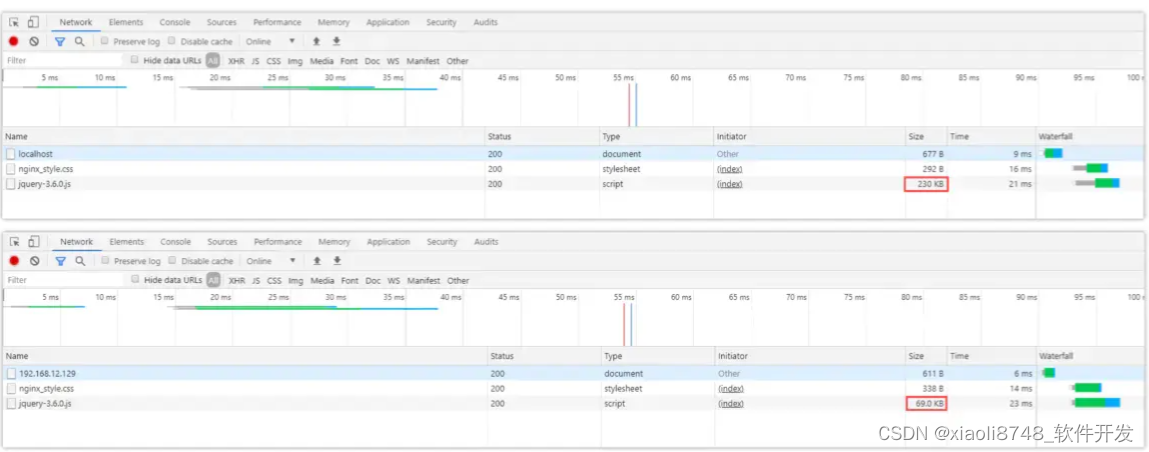
深入浅出 -- 系统架构之负载均衡Nginx资源压缩
一、Nginx资源压缩 建立在动静分离的基础之上,如果一个静态资源的Size越小,那么自然传输速度会更快,同时也会更节省带宽,因此我们在部署项目时,也可以通过Nginx对于静态资源实现压缩传输,一方面可以节省带宽…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...
