备战蓝桥杯---数论相关问题
目录
一、最大公约数和最小公倍数
二、素数判断
三、同余
四、唯一分解定理
五、约数个数定理
六、约数和定理
五、快速幂
六、费马小定理
七、逆元
一、最大公约数和最小公倍数
文章链接:最大公约数和最小公倍数
二、素数判断
文章链接:在Java中判断素数
三、同余
同余是一个数学概念,它描述了两个数在某个特定的模下具有相同的余数。在数学中,我们使用符号"≡"来表示同余关系。具体来说,对于给定的整数a、b和正整数m,如果a与b除以m得到的余数相等,即(a mod m) = (b mod m),我们就说a与b在模m下是同余的。
四、唯一分解定理
该定理表明,每个大于1的自然数都可以被唯一地表示为质数的乘积。
具体来说,唯一分解定理可以表述为:任何一个大于1的自然数n,都可以写成质数的乘积形式,即n = p1^a1 * p2^a2 * … * pk^ak,其中p1, p2, …, pk为质数,a1, a2, …, ak为正整数,并且这种表示方式是唯一的,即如果将n分解成不同的质数乘积形式,那么这些质数和指数也是唯一确定的。
例如,对于自然数12,它可以被分解为2^2 * 3^1,其中2和3都是质数,指数分别为2和1。而这种分解方式是唯一的,即12不能被表示为其他质数乘积的形式。
import java.util.ArrayList; import java.util.Arrays; import java.util.List; import java.util.Scanner;public class Main {static class node{int a,b;//a的b次方node(int a,int b){this.a=a;this.b=b;}}public static void main(String[] args){Scanner scanner=new Scanner(System.in);int n=scanner.nextInt();//输入的数,输出是由多个质数的次方的乘积int t=n;ArrayList<node> e=new ArrayList<>();for(int i=2;i<=n/i;i++){if(n%i==0){int ans=0;while(n%i==0){ans++;n/=i;}e.add(new node(i,ans));}}if(n>1){e.add(new node(n,1));}System.out.print(t+"=");for(int i=0;i<e.size();i++){if(i==e.size()-1){System.out.print(e.get(i).a+"^"+e.get(i).b);break;}System.out.print(e.get(i).a+"^"+e.get(i).b+"+");}} }
五、约数个数定理
约数个数定理是数论中的一个重要定理,它给出了一个正整数的约数个数与其质因数分解有关的关系。具体来说,如果一个正整数n可以分解为质数的乘积,即n = p1^a1 * p2^a2 * … * pk^ak,其中p1、p2、…、pk为不同的质数,a1、a2、…、ak为正整数,则n的约数个数可以通过以下公式计算:
约数个数 = (a1 + 1) * (a2 + 1) * … * (ak + 1)
其中,(a1 + 1)、(a2 + 1)、…、(ak + 1)分别表示每个质因数的指数加1后的值。
例如,对于正整数12,它可以分解为2^2 * 3^1,因此它的约数个数为(2+1) * (1+1) = 6。它的约数包括1、2、3、4、6和12。
六、约数和定理
通过某一个数字的唯一分解定理,可以推出约数和定理。约数和定理是指对于任意一个正整数n,它的所有约数的个数可以通过对n进行唯一分解后的指数加1的乘积来计算。
具体来说,如果将正整数n进行唯一分解,得到其质因数分解式为: n = p1^a1 * p2^a2 * p3^a3 * … * pk^ak 其中,p1, p2, p3, …, pk为不同的质数,a1, a2, a3, …, ak为对应的指数。
根据唯一分解定理,n的所有约数可以通过对指数进行组合得到。对于每个质因数pi,它的指数ai可以取0到ai之间的任意整数,这样就可以得到ai+1个选择。因此,n的所有约数的个数为(a1+1) * (a2+1) * (a3+1) * … * (ak+1)。
以20为例,将20进行唯一分解得到其质因数分解式为: 20 = 2^2 * 5^1 其中,2和5为不同的质数,指数分别为2和1。
根据约数和定理,20的所有约数的个数为(2+1) * (1+1) = 6。即20的约数有6个,分别为1、2、4、5、10和20。
也就是:
(1)2^0*5^0=1
(2)2^0*5^1=5
(3)2^1*5^0=2
(4)2^1*5^1=10
(5)2^2*5^0=4
(6)2^2*5^1=20
五、快速幂
文章链接:快速幂(Java实现)
六、费马小定理
费马小定理是数论中的一个重要定理,它描述了在模运算下的一种特殊性质。具体来说,费马小定理表明,如果p是一个质数,a是任意整数且不是p的倍数,那么a的p-1次方除以p的余数等于1。
数学表达式为:a^(p-1) ≡ 1 (mod p)------>(a^(p-1))%p=1(简单来说)
这里的“≡”表示模运算下的等价关系,即两个数除以p的余数相等。
举个例子来说明,假设p=7,a=3,根据费马小定理,我们可以计算3^6除以7的余数。计算过程如下:
3^6 = 729 729 ÷ 7 = 104 余 1
因此,根据费马小定理,3^6除以7的余数等于1。
七、逆元
逆元是数论中的一个重要概念,它指的是在模运算下,对于给定的整数a和模数m,存在一个整数b,使得(a * b) % m = 1。其中,a称为原元,b称为a的逆元。
举个例子来说明逆元的概念。假设我们要求解在模7下的逆元,即找到一个整数b,使得(a * b) % 7 = 1。如果我们取a = 3,那么可以发现3 * 5 = 15,15除以7的余数为1,所以5就是3在模7下的逆元。因此,5是3的逆元。
相关文章:

备战蓝桥杯---数论相关问题
目录 一、最大公约数和最小公倍数 二、素数判断 三、同余 四、唯一分解定理 五、约数个数定理 六、约数和定理 五、快速幂 六、费马小定理 七、逆元 一、最大公约数和最小公倍数 文章链接:最大公约数和最小公倍数 二、素数判断 文章链接:在J…...
苹果手表Apple Watch录了两个半小时的录音,却只能播放4秒,同步到手机也一样,还能修复好吗?
好多人遇到这个情况,用苹果手表Apple Watch录音,有的录1个多小时,有的录了3、4小时,甚至更长时间,因为手表没电,忘记保存等原因造成录音损坏,都是只能播放4秒,同步到手机也一样&…...
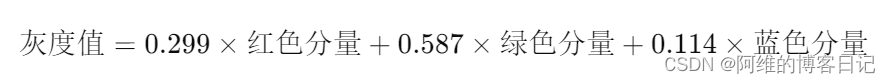
RGB三通道和灰度值的理解
本文都是来自于chatGPT的回答!!! 目录 Q1:像素具有什么属性?Q2:图像的色彩是怎么实现的?Q3:灰度值和颜色值是一个概念吗?Q4:是不是像素具有灰度值,也有三个颜色分量RGB?Q5:灰度图像是没有色彩的吗?Q6: 彩色图像是既具有灰度值也具有RGB三…...

ARM、X86、RISC-V三分天下
引入: 简单的介绍一下X86、ARM、RISC-V三种cpu架构的区别和应用场景。 目录 简单概念讲解 1. X86架构 2. ARM架构 3. RISC-V架构 应用场景 X86、ARM和RISC-V是三种不同的CPU架构,它们在设计理念、指令集和应用场景上有一些区别。 简单概念讲解 1. X…...
力控机器人原理及力控制实现
力控机器人原理及力控制实现 力控机器人是一种能够感知力量并具有实时控制能力的机器人系统。它们可以在与人类进行精准协作和合作时,将力传感技术(Force Sensing Technology)和控制算法(Control Algorithm)结合起来&a…...

最小生成树
最小生成树问题是指给定一个带权的无向图,删除一些边使得这个无向图变成一棵树,并且权值之和最小。 解决此类问题的方法主要有两种:Prim算法,Kruskal算法 Prim 算法 从一个点开始,逐步扩展,每次选择权值…...

二维动画制作软件 Animate 2024 for mac激活版
Animate 2024 for Mac是一款功能强大的二维动画制作软件,专为Mac用户打造。它提供了丰富的动画编辑功能,使用户能够轻松创建出生动逼真的动画作品。无论是短片、广告还是游戏等应用领域,Animate 2024都能发挥出出色的表现。 软件下载…...
相对论中关于光速不变理解的补充
近几个月在物理直播间聊爱因斯坦相对论,发现好多人在理解爱因斯坦相对论关于基本假设,普遍认为光速是不变的,质能方程 中光速的光速不变的,在这里我对这个假设需要做一个补充,他是基于质能方程将光速C 在真是光速变化曲…...

面试(04)————JavaWeb
1、网络通讯部分 1.1、 TCP 与 UDP 区别? 1.2、什么是 HTTP 协议? 1.3、TCP 的三次握手,为什么? 1.4、HTTP 中重定向和请求转发的区别? 1.5、 Get 和 Post 的区别? 2、cookie 和 session 的区别&am…...
Debian12 使用 nginx 与 php8.2 使用 Nextcloud
最近将小服务器升级了下系统,使用了 debian12 的版本,正好试试 nginx 和 php-fpm 这种方式运行 Nextcloud 这个私有云的配置。 一、基本系统及应用安装 系统:debian12 x86_64 位版本最小安装,安装后可根据自己需求安装一些工具&…...

Java设计模式:代理模式的静态和动态之分(八)
码到三十五 : 个人主页 心中有诗画,指尖舞代码,目光览世界,步履越千山,人间尽值得 ! 在软件设计中,代理模式是一种常用的设计模式,它为我们提供了一种方式来控制对原始对象的访问。在Java中&a…...

【论文通读】AgentStudio: A Toolkit for Building General Virtual Agents
AgentStudio: A Toolkit for Building General Virtual Agents 前言AbstractMotivationFramework评估GUI GroudingReal-World Cross-Application Benchmark Suite Conclusion 前言 来自昆仑万维的一篇智能体环境数据大一统框架工作,对未来计算机智能体的发展具有指…...

wordvect嵌入和bert嵌入的区别
Word2Vec 嵌入和 BERT 嵌入之间有几个关键区别: 训练方式: Word2Vec:Word2Vec 是一个基于神经网络的词嵌入模型,它通过训练一个浅层的神经网络来学习单词的分布式表示。它有两种训练方式:连续词袋模型(CBOW…...

渗透测试练习题解析 5(CTF web)
1、[安洵杯 2019]easy_serialize_php 1 考点:PHP 反序列化逃逸 变量覆盖 【代码审计】 通过 GET 的方式获取参数 f 的值,传递给变量 function 定义一个过滤函数,过滤掉特定字符(用空字符替换) 下面的代码其实没什么用…...
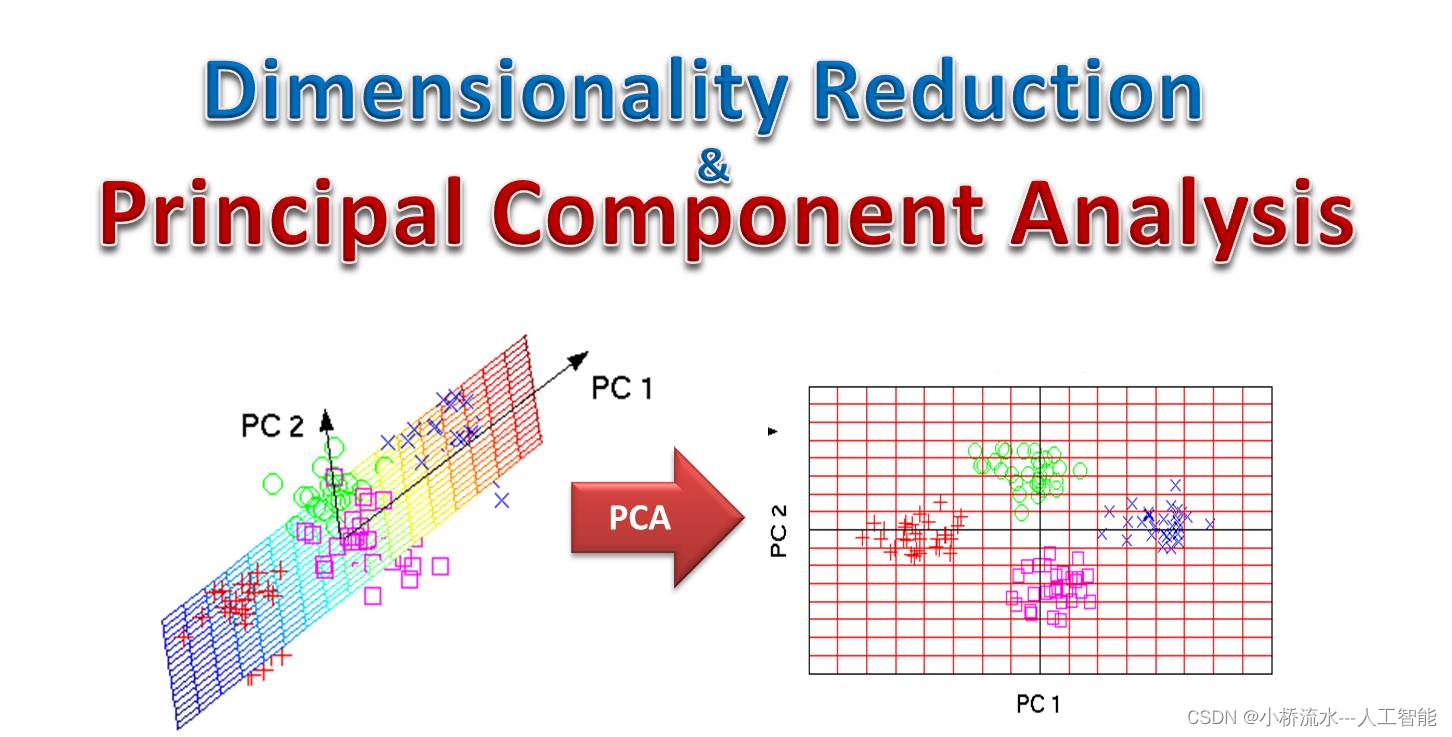
PCA(Principal Component Analysis,主成分分析)
PCA(Principal Component Analysis,主成分分析)是一种在数据分析中广泛应用的统计方法,主要用于数据降维、可视化和去噪。以下是对PCA的发展史、工作原理以及理论基础的详细解释: Principal Component Analysis 一、PC…...
干货 | 探索CUTTag:从样本到文库,实验步步为营!
CUT&Tag(Cleavage Under Targets and Tagmentation)是一种新型DNA-蛋白互作研究技术,主要用于研究转录因子或组蛋白修饰在全基因组上的结合或分布位点。相比于传统的ChIP-seq技术,CUT&Tag反应在细胞内进行,创新…...

提质不增本,降本不降质
#公益巡讲# #质量万里行# 公开课、沙龙活动...

数据结构---顺序表实现
目录 1.顺序表 2.动态顺序表的实现 (4)顺序表初始化 (5)顺序表销毁 (6)顺序表的插入 a.尾插 b.头插 (7)顺序表的删除 a.尾删 b.头删 (8)指定位置之…...

python docx 添加动态表格
在Python中,使用python-docx库可以创建Word文档并添加动态表格。以下是一个简单的例子,演示如何创建一个包含动态内容的表格: from docx import Document# 创建一个Word文档 document Document()# 添加一个标题 document.add_heading(动态表…...
git配置多SSH
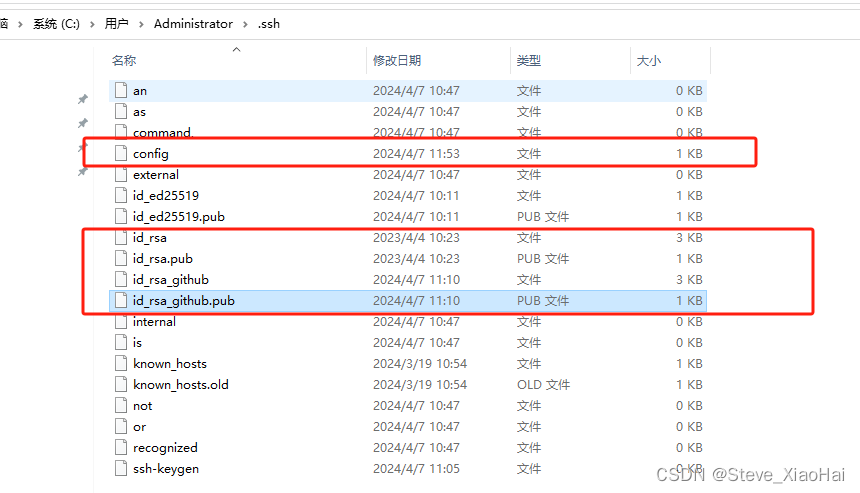
目的: 一台电脑可以让github、gitee等账号同时存在,让不同账号配置不同的密钥 第一步:创建不同平台的SSH公钥 执行命令: ssh-keygen -t rsa -C "对应仓库邮箱地址" -f ~/.ssh/id_rsa.github 如果执行上面的命令&…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...
