【洛谷】P9236 [蓝桥杯 2023 省 A] 异或和之和
题目链接
P9236 [蓝桥杯 2023 省 A] 异或和之和 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
思路
1. 暴力求解
直接枚举出所有子数组,求每个子数组的异或和,再对所有的异或和求和
枚举所有子数组的时间复杂度为O(N^2),求每个子数组的异或和又要遍历一次数组,所以总的时间复杂度为O(N^3)
2. 优化
异或中有这么一个性质:a ^ b ^ b = a,即两个相同元素异或后为0,此性质推广到子数组同理
因此我们可以用前缀和的思想来快速得出一个区间的异或和。
此时可以将时间复杂度优化为O(N^2)
基于前缀和,我们进行进一步的优化:拆位法和贡献法
(1)拆位法
拆位法:将一个数转换成二进制形式,并拆分成单独的二进制位来计算
二进制中除了0就是1,由于异或的性质,我们可以得出一个结论:对于二进制位中的第i位而言,如果这一位中1的个数为奇数,那么异或后的结果中这一位就是1,否则为0
例如:
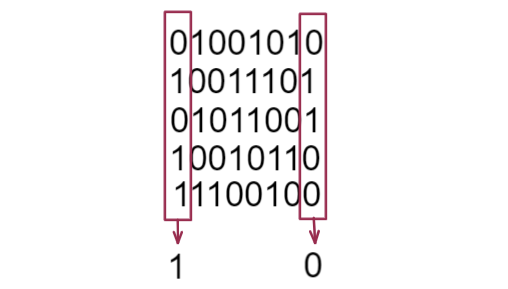
拆位法加上前缀和,我们就能计算出某个区间中1的个数,进而得出在该区间中这个二进制位异或后是0还是1
(2)贡献法
贡献法:从区间的角度转换成计算每个二进制位对答案的贡献
某个区间中,这一位异或后的结果为1时,这一位就产生了贡献;异或后的结果为0时这一位就不会产生贡献。
例如:

我们以一个二进制位作为一个计算周期,统计该位中1的前缀和

例如该位中1的前缀和为偶数,说明对于虚线内的这个区间,异或后该位为0,无贡献
注意:这里的区间最终异或后只可能为1或0,因此当我们谈论区间的贡献时,实际上也就是谈论该位是否有贡献
但是如果一个前缀和为偶数的区间减去一个前缀和为奇数的区间,所得到的新的区间的前缀和也为奇数,即新区间中该位异或后的结果为1,有贡献
例如:
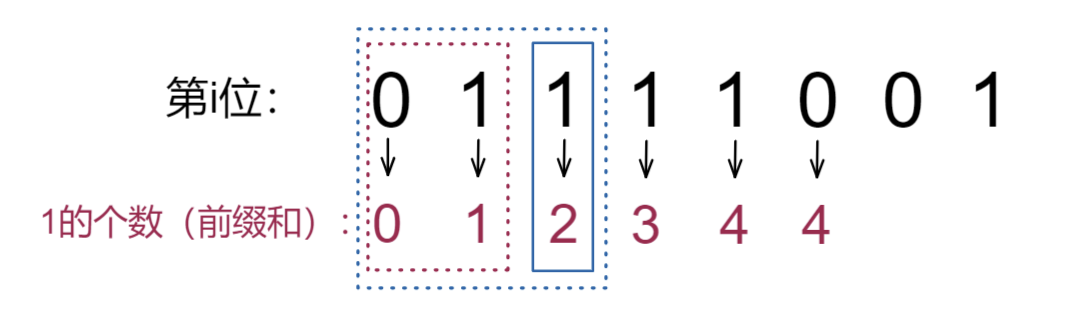
蓝色虚线的区间前缀和为偶数(2),减去红色虚线前缀和为奇数(1)的区间,所得到蓝色实线区间的1的前缀和为奇数(2 - 1 = 1),则该实线区间异或后也有贡献
通过观察,我们可以得出以下结论:
对于第i个二进制位,如果以第n个数为结尾的区间所对的前缀和为偶数时,该区间能够提供 前面奇数前缀和的个数 个贡献区间
例如对于上面蓝色虚线的区间,其前面有一个奇数前缀和,那么该区间自身就能提供一个贡献区间

而该位中1的前缀和为奇数,与上面同理,我们只需要计算出前面所有前缀和为偶数的区间个数,减去这些前缀和为偶数的区间得到的新区间,前缀和都为奇数(奇-偶=奇),则都有贡献
而因为该区间本身的前缀和为奇数,所以能够提供的贡献区间为:1 + 前面偶数前缀和的个数
通过提示我们可以知道所有的数中有效位数不会超过20
![]()
代码
#include <bits/stdc++.h>
using namespace std;
#define ll long longll n;int main()
{cin >> n;ll *arr = new ll[n];for (int i = 0; i < n; i++)cin >> arr[i];ll pow = 1, sum = 0; for (int i = 0; i < 20; i++) //最多计算20个二进制位 {ll counti = 0, oddnum = 0, evenum = 0, range = 0; //counti统计1的前缀和,oddnum统计奇数前缀和的个数//evenum统计偶数前缀和的个数,range统计有贡献区间个数 for (int j = 0; j < n; j++) //遍历n个整数 {if (arr[j] & 1) //按位与1后结果为1,说明最低位为1,否则为0 counti++; //更新前缀和 if (counti % 2 == 1) //前缀和为奇数{range += 1 + evenum; //更新有贡献区间个数 oddnum++; //奇数前缀和的个数+1 }else //前缀和为偶数 {range += oddnum; //更新有贡献区间个数 evenum++; //偶数前缀和的个数+1 }arr[j] >>= 1; //移位 }sum += range * pow; //计算位数对结果的贡献值 pow *= 2; //更新pow }cout << sum;return 0;
}
讲的不够清楚也请大家多多见谅,有错误或问题可以在评论区指出。
相关文章:

【洛谷】P9236 [蓝桥杯 2023 省 A] 异或和之和
题目链接 P9236 [蓝桥杯 2023 省 A] 异或和之和 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 思路 1. 暴力求解 直接枚举出所有子数组,求每个子数组的异或和,再对所有的异或和求和 枚举所有子数组的时间复杂度为O(N^2)&…...

ThreadLocal加切面实现线程级别的方法缓存
1、实现效果 当一个请求线程多次请求A方法时,只会触发一次A方法的实际调用,会将方法结果缓存起来,避免多次调用。 2、实现过程 1. 需要一个注解ThreadLocalCache,在需要缓存的方法上加上该注解 2. 需要一个切面,借助ThreadLocal,将结果缓存起来,利用环绕通知来实现方法拦截从…...

使用 Flume 将 CSV 数据导入 Kafka:实现实时数据流
使用 Flume 将 CSV 数据导入 Kafka:实现实时数据流 文介绍了如何使用 Apache Flume 将 CSV 格式的数据从本地文件系统导入到 Apache Kafka 中,以实现实时数据流处理。通过 Flume 的配置和操作步骤,我们可以轻松地将数据从 CSV 文件中读取并发…...

对代理模式的理解
目录 一、前言二、案例1 代码2 自定义代理类【静态代理】2.1 一个接口多个实现,到底注入哪个依赖呢?2.1.1 Primary注解2.1.2 Resource注解(指定name属性)2.1.3 Qualifier注解 2.2 面向接口编程2.3 如果没接口咋办呢?2.…...
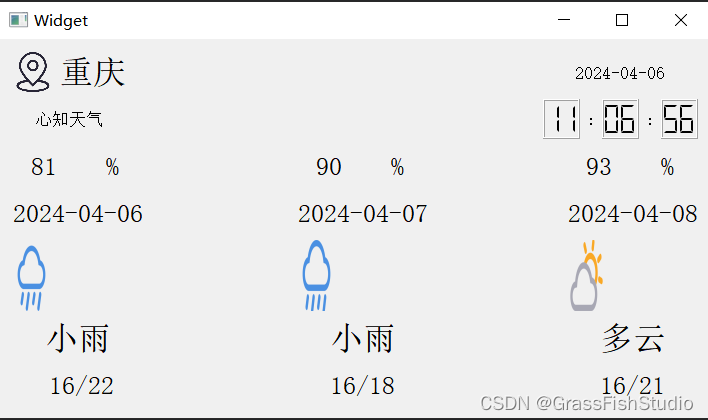
#QT项目实战(天气预报)
1.IDE:QTCreator 2.实验: 3.记录: (1)调用API的Url a.调用API获取IP whois.pconline.com.cn/ipJson.jsp?iphttp://whois.pconline.com.cn/ipJson.jsp?ip if(window.IPCallBack) {IPCallBack({"ip":&quo…...
数据挖掘|关联分析与Apriori算法详解
数据挖掘|关联分析与Apriori算法 1. 关联分析2. 关联规则相关概念2.1 项目2.2 事务2.3 项目集2.4 频繁项目集2.5 支持度2.6 置信度2.7 提升度2.8 强关联规则2.9 关联规则的分类 3. Apriori算法3.1 Apriori算法的Python实现3.2 基于mlxtend库的Apriori算法的Python实现 1. 关联分…...

ChatGPT Excel 大师
原文:ChatGPT Excel Mastery 译者:飞龙 协议:CC BY-NC-SA 4.0 序言 欢迎来到 Excel 掌握的变革之旅,在这里,尖端技术和永恒专业知识在“ChatGPT Excel 掌握:释放专家技巧和窍门的力量”中融合。在当今快节…...

C 语言中的 end, _end 符号
使用 man 3 end 可以看到相关符号的解释 这些符号不是在 C 语言文件和头文件中定义的,它们是 ld 在链接所有 .o 文件的时候自己添加的。 end 和 _end 的地址,就是最终程序的堆的起始地址 要打印它们的话,一个样例程序在下面: …...
绿联 安装PDF工具
这是一个强大的本地托管的基于 Web 的 PDF 操作工具,使用 docker,允许您对 PDF 文件执行各种操作,例如拆分、合并、转换、重组、添加图像、旋转、压缩等。这个本地托管的 Web 应用程序最初是 100% ChatGPT 制作的应用程序,现已发展…...

备战蓝桥杯---数论相关问题
目录 一、最大公约数和最小公倍数 二、素数判断 三、同余 四、唯一分解定理 五、约数个数定理 六、约数和定理 五、快速幂 六、费马小定理 七、逆元 一、最大公约数和最小公倍数 文章链接:最大公约数和最小公倍数 二、素数判断 文章链接:在J…...
苹果手表Apple Watch录了两个半小时的录音,却只能播放4秒,同步到手机也一样,还能修复好吗?
好多人遇到这个情况,用苹果手表Apple Watch录音,有的录1个多小时,有的录了3、4小时,甚至更长时间,因为手表没电,忘记保存等原因造成录音损坏,都是只能播放4秒,同步到手机也一样&…...
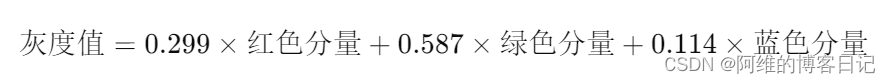
RGB三通道和灰度值的理解
本文都是来自于chatGPT的回答!!! 目录 Q1:像素具有什么属性?Q2:图像的色彩是怎么实现的?Q3:灰度值和颜色值是一个概念吗?Q4:是不是像素具有灰度值,也有三个颜色分量RGB?Q5:灰度图像是没有色彩的吗?Q6: 彩色图像是既具有灰度值也具有RGB三…...

ARM、X86、RISC-V三分天下
引入: 简单的介绍一下X86、ARM、RISC-V三种cpu架构的区别和应用场景。 目录 简单概念讲解 1. X86架构 2. ARM架构 3. RISC-V架构 应用场景 X86、ARM和RISC-V是三种不同的CPU架构,它们在设计理念、指令集和应用场景上有一些区别。 简单概念讲解 1. X…...
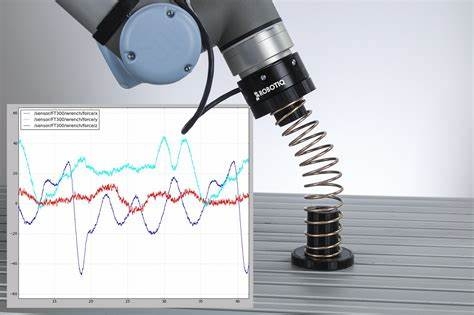
力控机器人原理及力控制实现
力控机器人原理及力控制实现 力控机器人是一种能够感知力量并具有实时控制能力的机器人系统。它们可以在与人类进行精准协作和合作时,将力传感技术(Force Sensing Technology)和控制算法(Control Algorithm)结合起来&a…...

最小生成树
最小生成树问题是指给定一个带权的无向图,删除一些边使得这个无向图变成一棵树,并且权值之和最小。 解决此类问题的方法主要有两种:Prim算法,Kruskal算法 Prim 算法 从一个点开始,逐步扩展,每次选择权值…...

二维动画制作软件 Animate 2024 for mac激活版
Animate 2024 for Mac是一款功能强大的二维动画制作软件,专为Mac用户打造。它提供了丰富的动画编辑功能,使用户能够轻松创建出生动逼真的动画作品。无论是短片、广告还是游戏等应用领域,Animate 2024都能发挥出出色的表现。 软件下载…...
相对论中关于光速不变理解的补充
近几个月在物理直播间聊爱因斯坦相对论,发现好多人在理解爱因斯坦相对论关于基本假设,普遍认为光速是不变的,质能方程 中光速的光速不变的,在这里我对这个假设需要做一个补充,他是基于质能方程将光速C 在真是光速变化曲…...

面试(04)————JavaWeb
1、网络通讯部分 1.1、 TCP 与 UDP 区别? 1.2、什么是 HTTP 协议? 1.3、TCP 的三次握手,为什么? 1.4、HTTP 中重定向和请求转发的区别? 1.5、 Get 和 Post 的区别? 2、cookie 和 session 的区别&am…...
Debian12 使用 nginx 与 php8.2 使用 Nextcloud
最近将小服务器升级了下系统,使用了 debian12 的版本,正好试试 nginx 和 php-fpm 这种方式运行 Nextcloud 这个私有云的配置。 一、基本系统及应用安装 系统:debian12 x86_64 位版本最小安装,安装后可根据自己需求安装一些工具&…...

Java设计模式:代理模式的静态和动态之分(八)
码到三十五 : 个人主页 心中有诗画,指尖舞代码,目光览世界,步履越千山,人间尽值得 ! 在软件设计中,代理模式是一种常用的设计模式,它为我们提供了一种方式来控制对原始对象的访问。在Java中&a…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...
