数据挖掘|关联分析与Apriori算法详解
数据挖掘|关联分析与Apriori算法
- 1. 关联分析
- 2. 关联规则相关概念
- 2.1 项目
- 2.2 事务
- 2.3 项目集
- 2.4 频繁项目集
- 2.5 支持度
- 2.6 置信度
- 2.7 提升度
- 2.8 强关联规则
- 2.9 关联规则的分类
- 3. Apriori算法
- 3.1 Apriori算法的Python实现
- 3.2 基于mlxtend库的Apriori算法的Python实现
1. 关联分析
关联规则分析(Association-rules Analysis)是数据挖掘领域的一个重要方法,它是以某种方式分析数据源,从数据样本集中发现一些潜在有用的信息和不同数据样本之间关系的过程。
关联是指在两个或多个变量之间存在某种规律性,但关联并不一定意味着因果关系。
关联规则是寻找在同一事件中出现的不同项目的相关性,关联分析是挖掘关联规则的过程。
比如在一次购买活动中所买不同商品的相关性。
关联分析即利用关联规则进行数据挖掘。
关联规则是形式如下的一种规则,“在购买计算机的顾客中,有30%的人也同时购买了打印机”。
从大量的商务事务记录中发现潜在的关联关系,可以帮助人们作出正确的商务决策。
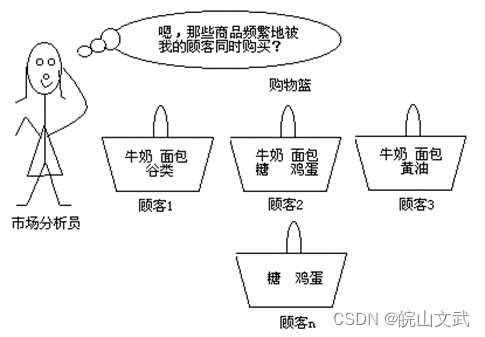
关联规则分析于1993年由美国IBM Almaden Research Center 的 Rakesh Agrawal 等人在进行市场购物篮分析时首先提出的,用以发现超市销售数据库中的顾客购买模式,现在已经广泛应用于许多领域。
早期关联分析用于分析零售企业顾客的购物行为模式,所以关联分析又被称为购物篮分析。
关联规则也可用于商品货架布置、销售配置、存货安排、购物路线设计、商品陈列设计、交叉销售以及根据购买模式对用户进行分类等方面。
比较经典的关联规则是啤酒和尿布的故事。
2. 关联规则相关概念
2.1 项目
集合 I = i 1 , i 2 , . . . , i m I={i_1,i_2,...,i_m} I=i1,i2,...,im称为项集合,其中 m m m为正整数, i k ( k = 1 , 2 , … , m ) i_k(k=1,2,…,m) ik(k=1,2,…,m)称为项目。
项目是一个从具体问题中抽象出的一个概念。在超市的关联规则挖掘问题中,项目表示各种商品,如旅游鞋等。
2.2 事务
由于在超市的关联规则挖掘中并不关心顾客购买的商品数量和价格等,因此顾客的一次购物可以用该顾客所购买的所有商品的名称来表示,称为事务,所有事务的集合构成关联规则挖掘的数据集,称为事务数据库。
关联规则挖掘的数据库记为 D D D,事务数据库 D D D中的每个元组称为事务。一条事务 T T T是 I I I中项目的集合。一条事务仅包含其涉及到的项目,而不包含项目的具体信息。在超级市场的关联规则挖掘问题中事务是顾客一次购物所购买的商品,但事务中并不包含这些商品的具体信息,如商品的数量、价格等。
2.3 项目集
项目集是由 I I I中项目构成的集合。若项目集包含的项目数为 k k k,则称此项目集为 k − k- k−项目集。任意的项目集 X X X和事务 T T T若满足 T ⊇ X T\supseteq X T⊇X,则称事务 T T T包含项目集 X X X。在超市的关联规则挖掘问题中项目集可以看成一个或多个商品的集合。若某顾客一次购买所对应的事务T包含项目集 X X X,就说该顾客在这次购物中购买了项目集 X X X中的所有商品。
2.4 频繁项目集
对任意的项目集 X X X,若事务数据库 D D D中的事务包含项目集 X X X的比例为 ε \varepsilon ε,则项目集的支持率为 ε \varepsilon ε,记为 s u p p o r t ( X ) = ε support(X)= \varepsilon support(X)=ε,其中包含项目集 X X X的事务数称为项目集 X X X的频度,记为 c o u n t ( X ) count(X) count(X)。若项目集 X X X的支持率大于或等于用户指定的最小支持率(minsupport),则项目集 X X X称为频繁项目集(或大项目集),否则项目集 X X X为非频繁项目集(或小项目集)。如果数据库 D D D中的事务数记为 ∣ D ∣ |D| ∣D∣,频繁项目集是至少被 ε ∣ D ∣ \varepsilon |D| ε∣D∣条事务包含的项目集.
2.5 支持度
关联规则是形如 U → V U\rightarrow V U→V的规则,其中 U 、 V U、V U、V为项集,且 U ∩ V = ∅ U\cap V = \emptyset U∩V=∅。项集 U 、 V U、V U、V不一定包含于同一个项集合 I I I。
关联规则的支持度 s ( U → V ) s(U\rightarrow V) s(U→V)和置信度 c ( U → V ) c(U\rightarrow V) c(U→V)是度量项目关联的重要指标,它们分别描述了一个关联规则的有用性和确定性。
在事务数据库 D D D中,关联规则 U → V U\rightarrow V U→V的支持度为:
s ( U → V ) = s u p p o r t c o u n t ( U ∪ V ) ∣ D ∣ s(U\rightarrow V)= \frac{support_{count}(U\cup V)}{|D|} s(U→V)=∣D∣supportcount(U∪V)
支持度描述了 X 、 Y X、Y X、Y这两个事务在事务集 D D D中同时出现(记为 X ∪ Y X\cup Y X∪Y)的概率。
2.6 置信度
关联规则 U → V U\rightarrow V U→V的置信度是指同时包含 X 、 V X、V X、V的事务数与包含 V V V的事务数之比,它用来衡量关联规则的可信程度。记为:
c ( U → V ) = s u p p o r t c o u n t ( U ∪ V ) s u p p o r t c o u n t ( U ) c(U\rightarrow V)= \frac{support_{count}(U\cup V)}{support_{count}(U)} c(U→V)=supportcount(U)supportcount(U∪V)
其中, s u p p o r t c o u n t ( U ∪ V ) support_{count}(U\cup V) supportcount(U∪V)是包含项集 U ∪ V U\cup V U∪V的事务数; s u p p o r t c o u n t ( U ) support_{count}(U) supportcount(U)是包含项集 U U U的事务数;
一般情况下,只有关联规则的置信度大于或等于预设的阈值,就说明了它们之间具有某种程度的相关性,这才是一条有价值的规则。
如果关联规则置信度大于或等于用户给定的最小置信度阈值,则称关联规则是可信的。
2.7 提升度
提升度(Lift)是指当销售一个商品A时,另一个商品B销售率会增加多少。计算公式为:
L i f t ( A → B ) = C d e n c e ( A → B ) s u p p o r t c o u n t ( A ) Lift(A \rightarrow B)=\frac{C_dence(A \rightarrow B)}{support_{count}(A)} Lift(A→B)=supportcount(A)Cdence(A→B)
假设关联规则’牛奶’ → \rightarrow →’鸡蛋’的置信度为C_dence(’牛奶’=>’鸡蛋’)=2/4,牛奶的支持度S_port(’牛奶’)=3/5,则’牛奶’和’鸡蛋’的支持度Lift(’牛奶’=>’鸡蛋’)=0.83。
- 当关联规则A=>B的提升度值大于1的时候,说明商品A卖得越多,B也会卖得越多;
- 当提升度等于1则意味着商品A和B之间没有关联;
- 当提升度小于1则意味着购买商品A反而会减少B的销量。
2.8 强关联规则
若关联规则 X → Y X\rightarrow Y X→Y的支持度和置信度分别大于或等于用户指定的最小支持率 m i n s u p p o r t minsupport minsupport和最小置信度 m i n c o n f i d e n c e minconfidence minconfidence,则称关联规则 X → Y X\rightarrow Y X→Y为强关联规则,否则称关联规则 X → Y X\rightarrow Y X→Y为弱关联规则。
关联规则挖掘的核心就是要找出事务数据库 D D D中的所有强相关规则。
2.9 关联规则的分类
关联规则可以分为布尔型和数值型。
布尔型关联规则处理的项目都是离散的,显示了这些变量之间的关系。
例如,性别=“女”——>职业=“秘书”。
数值型关联规则可以和多维关联或多层关联规则结合起来。对数值型属性进行处理,参考连续属性离散化方法或统计方法对其进行分割,确定划分的区间个数和区间宽度。数值型关联规则中也可以包含可分类型变量。
例如,性别=“女”——>平均收入>2300, 这里的收入是数值类型,所以是一个数值型关联规则。
基于规则中项目的抽象层次,可以分为单层关联规则和多层关联规则。项目(概念)通常具有层次性。
例如:
- 牛奶——>面包[20%, 60%]
- 酸牛奶——>黄面包[6%, 50%]
基于规则包含的项目维数,关联规则可以分为单维和多维两种。
单维关联规则处理单个项目的关系,多维关联规则处理多个项目之间的某些关系。
例如:
- 单维关联规则:buys(x,“diapers”)——>buys(x,“beers”)[0.5%, 60%]
- 多维关联规则:major(x,“CS”)^takes(x,“DB”)——>grade(x,“A”)[1%, 75%]
分离关联规则(dissociation rule),也称为负相关模式。
分离关联规则与一般的关联规则相似,知识在关联规则中出现项目的反转项,在购物篮分析中可发现不在一起购买的商品。
例如,购买牛奶的顾客一般不购买汽水。
3. Apriori算法
Apriori算法的基本思想是找出所有的频繁项集,然后由频繁项集产生强关联规则,这些规则必须满足最小支持度和最小置信度。
Apriori算法一般分为以下两个阶段:
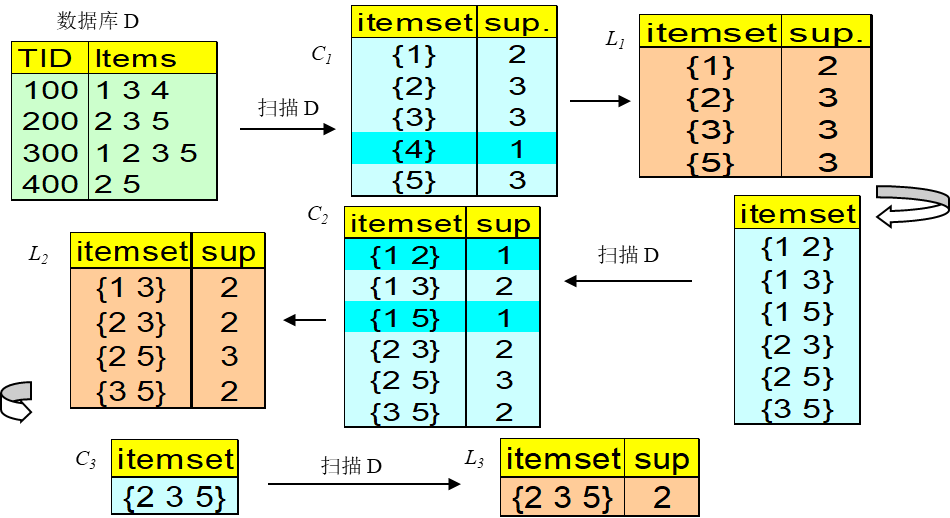
- 第一阶段:找出所有超出最小支持度的项集,形成频繁项集。
- 首先通过扫描数据集,产生一个大的候选项集,并计算每个候选项集发生的次数,然后基于预先给定的最小支持度生成一维项集 L 1 L_1 L1。再基于 L 1 L_1 L1和数据集中的事务,产生二维项集 L 2 L_2 L2;依此类推,直到生成 N N N维项集 L N L_N LN,并且已经不可能再生成满足最小支持度的 N + 1 N+1 N+1维项集。这样就依此产生项集 L 1 , L 2 , … , L N {L_1,L_2,…,L_N} L1,L2,…,LN。
- 第二阶段:利用频繁项集产生所需的规则。
- 对给定的 L L L,如果 L L L包含其非空子集 A A A,假设用户给定的最小支持度和最小置信度阈值分别为 m i n S _ p o r t minS\_port minS_port和 m i n C _ d e n c e minC\_dence minC_dence,并满足 m i n S _ p o r t ( L ) / m i n S _ p o r t ( A ) ≥ m i n C _ d e n c e minS\_port(L)/ minS\_port(A) \geq minC\_dence minS_port(L)/minS_port(A)≥minC_dence,则产生形式为 A = > L − A A=>L-A A=>L−A的规则。
在这两个阶段中,第一阶段是算法的关键。一旦找到了项集,关联规则的导出是自然的。事实上,我们一般只对满足一定的支持度和可信度的关联规则感兴趣。挖掘关联规则的问题就是产生支持度和置信度分别大于用户给定的最小支持度和最小置信度的关联规则。
3.1 Apriori算法的Python实现
import numpy as np
data_set = np.array([['鸡蛋','面包','西红柿','葱','蒜','牛奶'],
['面包','牛奶'],['鸡蛋','牛奶','豆角'],
['鸡蛋','牛奶','芹菜'],['鸡蛋','西红柿','豆角']],dtype=object)
def get_C1(data_set):C1 = set()for item in data_set:for l in item:C1.add(frozenset([l]))return C1
#data_set -- 数据集;C-- 候选集;min_support -- 最小支持度
def getLByC(data_set, C, min_support):L = {} #频繁项集和支持数for c in C:for data in data_set:if c.issubset(data):if c not in L:L[c] = 1else:L[c] += 1errorKeys=[]for key in L:support = L[key] / float(len(data_set))if support < min_support: #未达到最小支持数errorKeys.append(key)else:L[key] = supportfor key in errorKeys:L.pop(key)return L
'''根据频繁(k-1)项集自身连接产生候选K项集Ck并剪去不符合条件的候选L -- 频繁K-1项集
'''
def getCByL(L, k):len_L = len(L) #获取L的频繁项集数量L_keys = list(L.keys()) #获取L的键值C = set()for i in range(len_L):for j in range(1,len_L):l1 = list(L_keys[i])l1.sort()l2 = list(L_keys[j])l2.sort()if(l1[0:k-2] == l2[0:k-2]):C_item = frozenset(l1).union(frozenset(l2)) #取并集flag = True#判断C_item的子集是否在L_keys中for item in C_item:subC = C_item-frozenset([item])#获取C_item的子集if subC not in L_keys:#不在flag = Falseif flag == True:C.add(C_item)return C
def get_L(data_set, k, min_support):#C1较为特殊,先求C1 = get_C1(data_set)L1 = getLByC(data_set, C1, min_support)support_data = {}L = []L.append(L1)tempL = L1for i in range(2, k+1):Ci = getCByL(tempL, i)tempL = getLByC(data_set,Ci,min_support)L.append(tempL)for l in L:for key in l:support_data[key] = l[key]return L,support_data
#获取关联规则
def get_rule(L, support_data, min_support, min_conf):big_rules = []sub_sets= []for i in range(0, len(L)):for fset in L[i]:for sub_set in sub_sets:if sub_set.issubset(fset):conf = support_data[fset] / support_data[fset - sub_set]big_rule = (fset - sub_set, sub_set, conf)if conf >= min_conf and big_rule not in big_rules:big_rules.append(big_rule)sub_sets.append(fset)return big_rules
if __name__ == "__main__":min_support = 0.4 #最小支持度min_conf = 0.6 #最小置信度L,support_data = get_L(data_set, 3, min_support)#获取所有的频繁项集big_rule = get_rule(L, support_data, min_support, min_conf) #获取强关联规则print('==========所有的频繁项集如下===========')for l in L:for l_item in l:print(l_item, end=' ')print('支持度为:%f'%l[l_item])print('===========================================') for rule in big_rule:print(rule[0],'==>',rule[1],'\t\tconf = ',rule[2])==========所有的频繁项集如下===========
frozenset({'面包'}) 支持度为:0.400000
frozenset({'豆角'}) 支持度为:0.400000
frozenset({'西红柿'}) 支持度为:0.400000
frozenset({'鸡蛋'}) 支持度为:0.800000
frozenset({'牛奶'}) 支持度为:0.800000
===========================================
frozenset({'西红柿', '鸡蛋'}) 支持度为:0.400000
frozenset({'鸡蛋', '牛奶'}) 支持度为:0.600000
frozenset({'牛奶', '面包'}) 支持度为:0.400000
frozenset({'豆角', '鸡蛋'}) 支持度为:0.400000
===========================================
===========================================
frozenset({'西红柿'}) ==> frozenset({'鸡蛋'}) conf = 1.0
frozenset({'牛奶'}) ==> frozenset({'鸡蛋'}) conf = 0.7499999999999999
frozenset({'鸡蛋'}) ==> frozenset({'牛奶'}) conf = 0.7499999999999999
frozenset({'面包'}) ==> frozenset({'牛奶'}) conf = 1.0
frozenset({'豆角'}) ==> frozenset({'鸡蛋'}) conf = 1.0
3.2 基于mlxtend库的Apriori算法的Python实现
Sklearn库中没有Apriori算法。但是可以采用Python的第三方库实现Aprior算法发掘关联规则。相关的库有mlxtend机器学习包等,首先需要导入包含Apriori算法的mlxtend包:pip install mlxtend。
Apriori()函数常用形式为:
L,suppData=apriori(df, min_support=0.5,use_colnames=False,max_len=None)
参数说明:
- (1) df:表示给定的数据集。
- (2) min_support:表示给定的最小支持度。
- (3) use_colnames:默认False,表示返回的项集,用编号显示。如果值为True则直接显示项名称。
- (4) max_len:默认是None,表示最大项组合数,不做限制。如果只需要计算两个项集,可将这个值设置为2。
返回值:
- (1)L:返回频繁项集。
- (2)suppData:返回频繁项集的相应支持度。
示例代码如下:
from mlxtend.preprocessing import TransactionEncoder
from mlxtend.frequent_patterns import apriori
from mlxtend.frequent_patterns import association_rules
import pandas as pd
df_arr = [['鸡蛋','面包','西红柿','葱','蒜','牛奶'],
['面包','牛奶'],['鸡蛋','牛奶','豆角'],
['鸡蛋','牛奶','芹菜'],['鸡蛋','西红柿','豆角']]
#转换为算法可接受模型(布尔值)
te = TransactionEncoder()
df_tf = te.fit_transform(df_arr)
df = pd.DataFrame(df_tf,columns=te.columns_)
#设置支持度求频繁项集
frequent_itemsets = apriori(df,min_support=0.4,use_colnames= True)
#求关联规则,设置最小置信度为0.15
rules = association_rules(frequent_itemsets,metric = 'confidence',min_threshold = 0.6)
#设置最小提升度
rules = rules.drop(rules[rules.lift <0.6].index)
#设置标题索引并打印结果
rules.rename(columns = {'antecedents':'from','consequents':'to','support':'sup','confidence':'conf'},inplace = True)
rules = rules[['from','to','sup','conf','lift']]
print(rules)相关文章:

数据挖掘|关联分析与Apriori算法详解
数据挖掘|关联分析与Apriori算法 1. 关联分析2. 关联规则相关概念2.1 项目2.2 事务2.3 项目集2.4 频繁项目集2.5 支持度2.6 置信度2.7 提升度2.8 强关联规则2.9 关联规则的分类 3. Apriori算法3.1 Apriori算法的Python实现3.2 基于mlxtend库的Apriori算法的Python实现 1. 关联分…...

ChatGPT Excel 大师
原文:ChatGPT Excel Mastery 译者:飞龙 协议:CC BY-NC-SA 4.0 序言 欢迎来到 Excel 掌握的变革之旅,在这里,尖端技术和永恒专业知识在“ChatGPT Excel 掌握:释放专家技巧和窍门的力量”中融合。在当今快节…...

C 语言中的 end, _end 符号
使用 man 3 end 可以看到相关符号的解释 这些符号不是在 C 语言文件和头文件中定义的,它们是 ld 在链接所有 .o 文件的时候自己添加的。 end 和 _end 的地址,就是最终程序的堆的起始地址 要打印它们的话,一个样例程序在下面: …...
绿联 安装PDF工具
这是一个强大的本地托管的基于 Web 的 PDF 操作工具,使用 docker,允许您对 PDF 文件执行各种操作,例如拆分、合并、转换、重组、添加图像、旋转、压缩等。这个本地托管的 Web 应用程序最初是 100% ChatGPT 制作的应用程序,现已发展…...

备战蓝桥杯---数论相关问题
目录 一、最大公约数和最小公倍数 二、素数判断 三、同余 四、唯一分解定理 五、约数个数定理 六、约数和定理 五、快速幂 六、费马小定理 七、逆元 一、最大公约数和最小公倍数 文章链接:最大公约数和最小公倍数 二、素数判断 文章链接:在J…...
苹果手表Apple Watch录了两个半小时的录音,却只能播放4秒,同步到手机也一样,还能修复好吗?
好多人遇到这个情况,用苹果手表Apple Watch录音,有的录1个多小时,有的录了3、4小时,甚至更长时间,因为手表没电,忘记保存等原因造成录音损坏,都是只能播放4秒,同步到手机也一样&…...
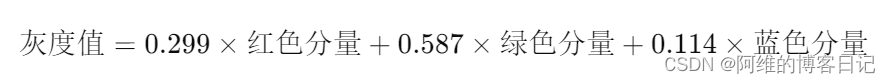
RGB三通道和灰度值的理解
本文都是来自于chatGPT的回答!!! 目录 Q1:像素具有什么属性?Q2:图像的色彩是怎么实现的?Q3:灰度值和颜色值是一个概念吗?Q4:是不是像素具有灰度值,也有三个颜色分量RGB?Q5:灰度图像是没有色彩的吗?Q6: 彩色图像是既具有灰度值也具有RGB三…...

ARM、X86、RISC-V三分天下
引入: 简单的介绍一下X86、ARM、RISC-V三种cpu架构的区别和应用场景。 目录 简单概念讲解 1. X86架构 2. ARM架构 3. RISC-V架构 应用场景 X86、ARM和RISC-V是三种不同的CPU架构,它们在设计理念、指令集和应用场景上有一些区别。 简单概念讲解 1. X…...
力控机器人原理及力控制实现
力控机器人原理及力控制实现 力控机器人是一种能够感知力量并具有实时控制能力的机器人系统。它们可以在与人类进行精准协作和合作时,将力传感技术(Force Sensing Technology)和控制算法(Control Algorithm)结合起来&a…...

最小生成树
最小生成树问题是指给定一个带权的无向图,删除一些边使得这个无向图变成一棵树,并且权值之和最小。 解决此类问题的方法主要有两种:Prim算法,Kruskal算法 Prim 算法 从一个点开始,逐步扩展,每次选择权值…...

二维动画制作软件 Animate 2024 for mac激活版
Animate 2024 for Mac是一款功能强大的二维动画制作软件,专为Mac用户打造。它提供了丰富的动画编辑功能,使用户能够轻松创建出生动逼真的动画作品。无论是短片、广告还是游戏等应用领域,Animate 2024都能发挥出出色的表现。 软件下载…...
相对论中关于光速不变理解的补充
近几个月在物理直播间聊爱因斯坦相对论,发现好多人在理解爱因斯坦相对论关于基本假设,普遍认为光速是不变的,质能方程 中光速的光速不变的,在这里我对这个假设需要做一个补充,他是基于质能方程将光速C 在真是光速变化曲…...

面试(04)————JavaWeb
1、网络通讯部分 1.1、 TCP 与 UDP 区别? 1.2、什么是 HTTP 协议? 1.3、TCP 的三次握手,为什么? 1.4、HTTP 中重定向和请求转发的区别? 1.5、 Get 和 Post 的区别? 2、cookie 和 session 的区别&am…...
Debian12 使用 nginx 与 php8.2 使用 Nextcloud
最近将小服务器升级了下系统,使用了 debian12 的版本,正好试试 nginx 和 php-fpm 这种方式运行 Nextcloud 这个私有云的配置。 一、基本系统及应用安装 系统:debian12 x86_64 位版本最小安装,安装后可根据自己需求安装一些工具&…...

Java设计模式:代理模式的静态和动态之分(八)
码到三十五 : 个人主页 心中有诗画,指尖舞代码,目光览世界,步履越千山,人间尽值得 ! 在软件设计中,代理模式是一种常用的设计模式,它为我们提供了一种方式来控制对原始对象的访问。在Java中&a…...

【论文通读】AgentStudio: A Toolkit for Building General Virtual Agents
AgentStudio: A Toolkit for Building General Virtual Agents 前言AbstractMotivationFramework评估GUI GroudingReal-World Cross-Application Benchmark Suite Conclusion 前言 来自昆仑万维的一篇智能体环境数据大一统框架工作,对未来计算机智能体的发展具有指…...

wordvect嵌入和bert嵌入的区别
Word2Vec 嵌入和 BERT 嵌入之间有几个关键区别: 训练方式: Word2Vec:Word2Vec 是一个基于神经网络的词嵌入模型,它通过训练一个浅层的神经网络来学习单词的分布式表示。它有两种训练方式:连续词袋模型(CBOW…...

渗透测试练习题解析 5(CTF web)
1、[安洵杯 2019]easy_serialize_php 1 考点:PHP 反序列化逃逸 变量覆盖 【代码审计】 通过 GET 的方式获取参数 f 的值,传递给变量 function 定义一个过滤函数,过滤掉特定字符(用空字符替换) 下面的代码其实没什么用…...
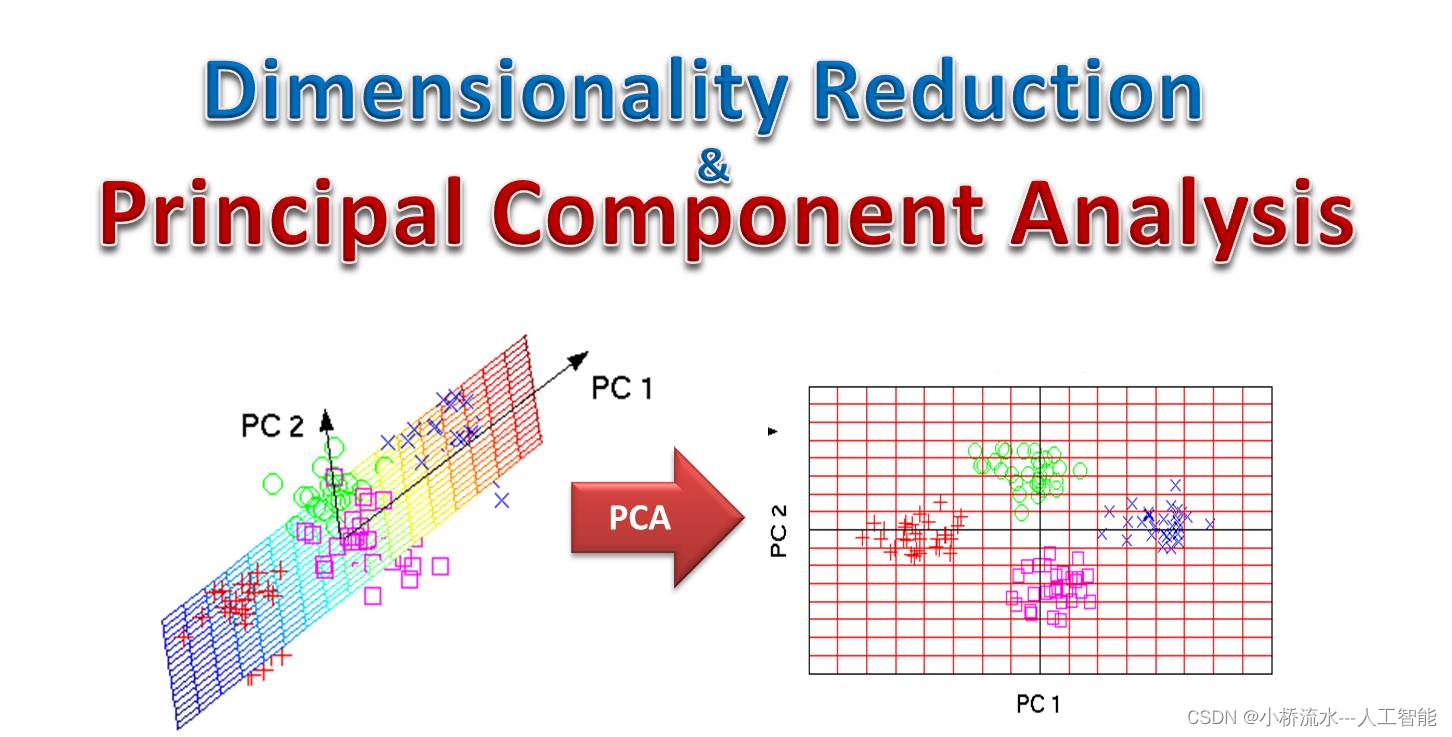
PCA(Principal Component Analysis,主成分分析)
PCA(Principal Component Analysis,主成分分析)是一种在数据分析中广泛应用的统计方法,主要用于数据降维、可视化和去噪。以下是对PCA的发展史、工作原理以及理论基础的详细解释: Principal Component Analysis 一、PC…...
干货 | 探索CUTTag:从样本到文库,实验步步为营!
CUT&Tag(Cleavage Under Targets and Tagmentation)是一种新型DNA-蛋白互作研究技术,主要用于研究转录因子或组蛋白修饰在全基因组上的结合或分布位点。相比于传统的ChIP-seq技术,CUT&Tag反应在细胞内进行,创新…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...
