工业4g路由器联网后迅速掉线是什么原因?
工业4G路由器连接上网后迅速掉线可能是由多种因素造成的。以下是一些建议的检查和解决步骤:
1、信号问题:
信号强度:检查工业路由器信号强度指示灯,如果信号弱,尝试移动路由器位置或添加外部天线来增强信号。
网络拥堵:如果路由器信号较强但仍然频繁掉线,可能是因为网络拥堵。尝试减少同一网络下同时进行的数据传输任务,或避开网络高峰时段进行连接,以及尝试更换频段。
2、SIM卡问题:
确保SIM卡没过期、余额充足且未被运营商锁定。
尝试将SIM卡放入手机或其他设备中检查是否还会掉线。
3、硬件问题:
路由器故障:路由器本身可能存在硬件问题,尝试重启或重置路由器,如果问题持续存在,可能需要修理或更换。
电源不稳定:确保路由器的电源适配器和电源线连接良好,电源供应稳定。
4、固件问题:
检查路由器固件版本,可能存在bug导致掉线,尝试更新到最新版本。
5、配置问题:
重新检查APN设置和其他网络参数,确保与运营商提供的设置一致。
检查是否有自动断线的设置,例如设置了连接时间限制或数据使用限制。
6、温度问题:
工业路由器在高温环境下工作可能会导致设备过热,尝试降温或改善散热条件。
7、软件冲突:
如果路由器运行了其他网络服务,如防火墙或流量管理软件,可能会与拨号上网功能有冲突。请检查相应设置或暂时禁用这些服务。

相关文章:

工业4g路由器联网后迅速掉线是什么原因?
工业4G路由器连接上网后迅速掉线可能是由多种因素造成的。以下是一些建议的检查和解决步骤: 1、信号问题: 信号强度:检查工业路由器信号强度指示灯,如果信号弱,尝试移动路由器位置或添加外部天线来增强信号。 网络拥…...

腾讯云4核8G服务器12M带宽646元1年零3个月,4C8G使用场景说明
腾讯云4核8G服务器多少钱?腾讯云4核8G轻量应用服务器12M带宽租用价格646元15个月,活动页面 txybk.com/go/txy 活动链接打开如下图所示: 腾讯云4核8G服务器优惠价格 这台4核8G服务器是轻量应用服务器,详细配置为:轻量4核…...

java - 读取配置文件
文章目录 1. properties2. XML(1) dom4j(2) XPath 1. properties // 创建properties对象用于读取properties文件Properties properties new Properties();properties.load(new FileReader("src/main/resources/test.properties"));String name properties.getPrope…...
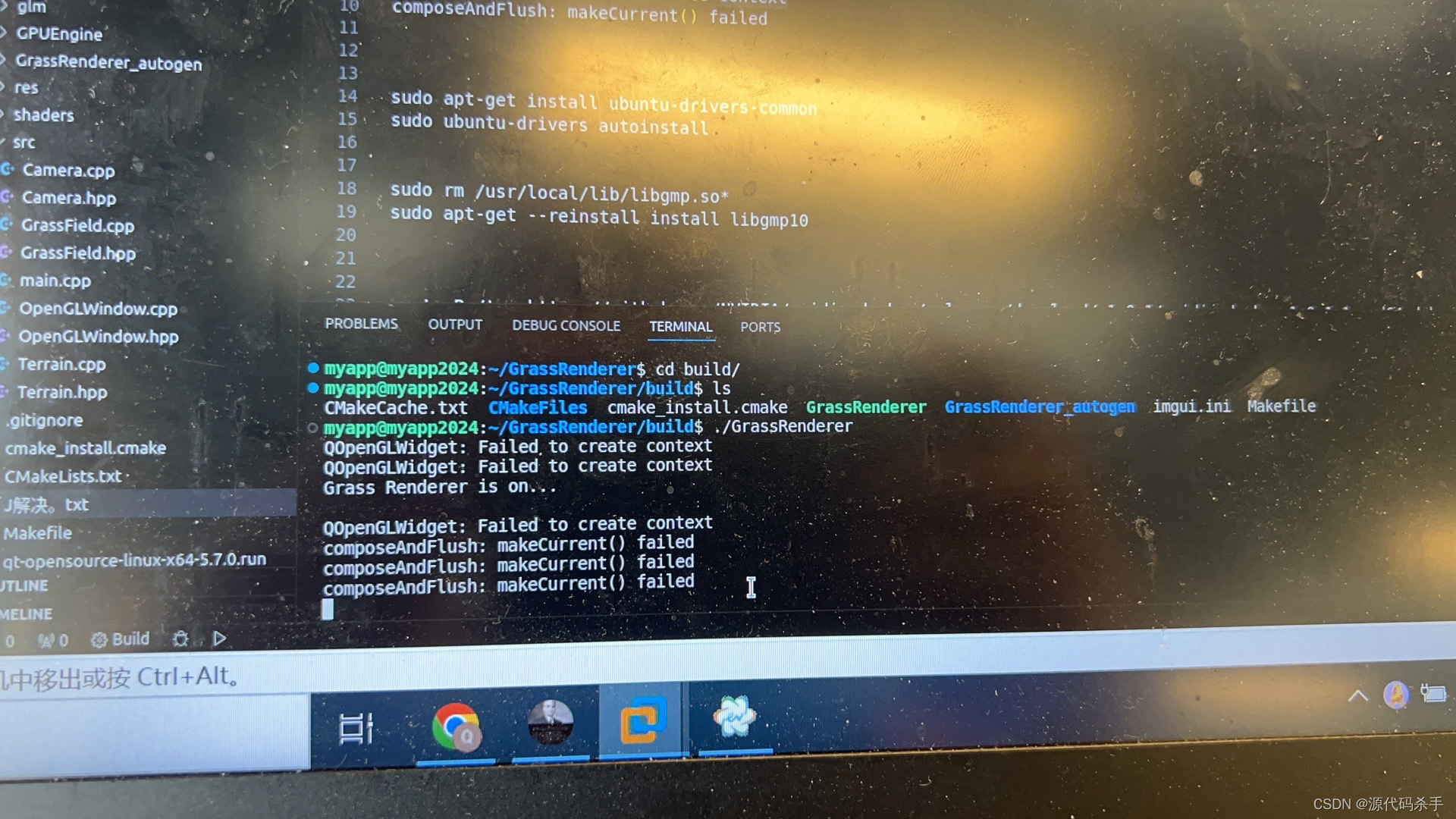
Ubuntu22.04平台编译完美解决问题“error: GLSL 4.5 is not supported.”【GLSL(OpenGL着色器语言)】
GLSL介绍 GLSL(OpenGL着色器语言)是用于编写OpenGL着色器程序的语言。GLSL 4.5 是 GLSL 的一个版本,引入了许多新的特性和改进,旨在提高着色器编程的灵活性和性能。GLSL 4.5 工具通常是用于编写、调试和优化 GLSL 4.5 着色器代码…...

数据结构之搜索二叉树与关联性容器初接触
一、搜索二叉树 1>、前言 1. map和set特性需要先铺垫二叉搜索树,而二叉搜索树也是一种树形结构 2. 二叉搜索树的特性了解,有助于更好的理解map和set的特性。 2>、概念 二叉搜索树又称二叉排序树,它或者是一棵空树,或者…...

C语言整数和小数的存储
1.整数在内存中的存储 计算机使用二进制进行存储、运算,整数在内存中存储使用的是二进制补码 1.1原码、反码、补码 整数的2进制表⽰⽅法有三种,即 原码、反码和补码 三种表⽰⽅法均有符号位和数值位两部分,符号位都是⽤0表⽰“正”&am…...

Games101Homework【6】Acceleration structure(Including framework analysis)
Code Analysis: friend: C中友元(友元函数和友元类)的用法和功能_friend class a<b>-CSDN博客 [C:不如Coding](11):友元函数与友元类_哔哩哔哩_bilibili Here is a simple…...

应用运维文档1
统一nginx接入配置指南 Nginx配置规范 1:不带微服务编码上下文至后端,以metadata-ui为例 location段配置信息,location配置中维护微服务编码上下文信息 # app_code: metadata-ui 流水线名称: metadata-ui location ~ ^/metadata-ui/(?P.*) {set $app_code metadata-ui;p…...

手机如何在线制作gif?轻松一键在线操作
现在大家都喜欢使用手机来拍摄记录有趣的事物,但是时间长了手机里的视频越来越多导致手机存储空间不够了,这些视频又不想删除时应该怎么办呢?这个很简单,下面就给大家分享一款不用下载手机就能操作的视频转gif网站-GIF中文网&…...

ChatGPT 在做什么,为什么有效?
原文:What Is ChatGPT Doing … and Why Does It Work? 译者:飞龙 协议:CC BY-NC-SA 4.0 序言 这本简短的书试图从第一原理解释 ChatGPT 是如何工作的。在某种程度上,这是关于技术的故事。但它也是关于科学的故事。以及关于哲学…...
Linux实验2 初步使用shell
一:实验目的 学习Linux下的文件系统结构,了解最基本的Linux下的shell命令操作,例如ls, cd, cat等各种指令操作。 学习vim编辑器的使用方式,学习如何使用ssh连接远程服务器。 二:实验内容 1.请指出下面每…...
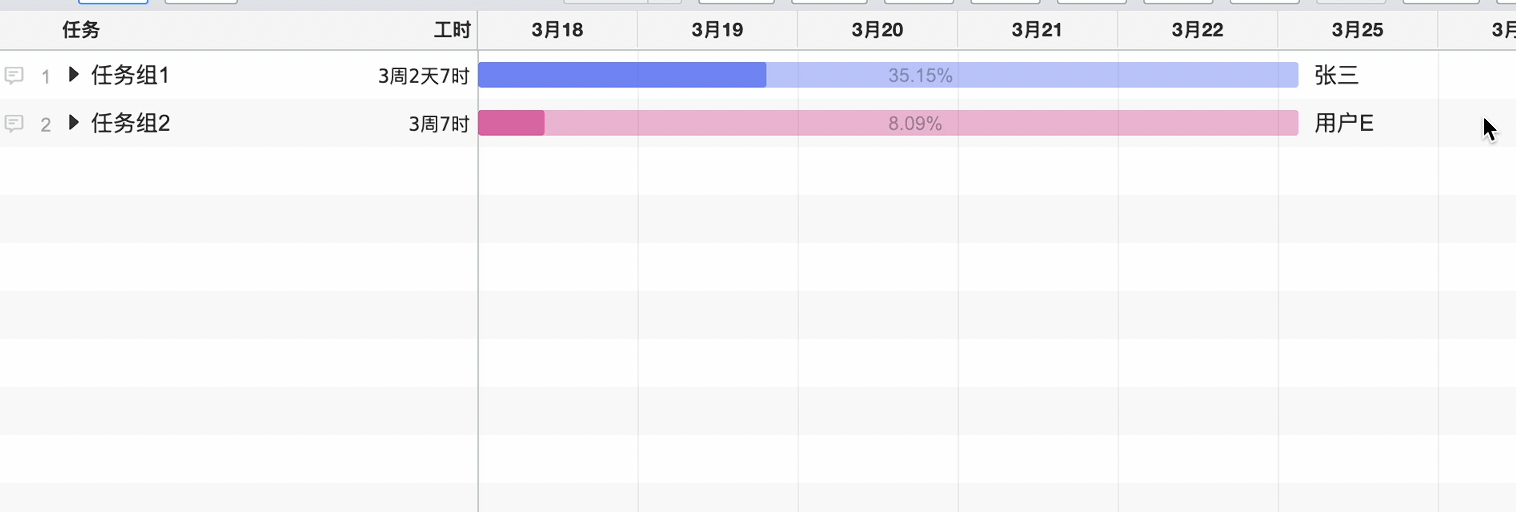
甘特图/横道图制作技巧 - 任务组
在甘特图中通过合理的任务分组可以让项目更加清晰,修改也更方便。 列如下面的甘特图一眼不太容易看清楚整体的进度。或者需要把所有的任务整体的延迟或者提前只能这样一个一个的任务调整,就比较麻烦。 通过给任务分组,看这上面整体的进度就…...
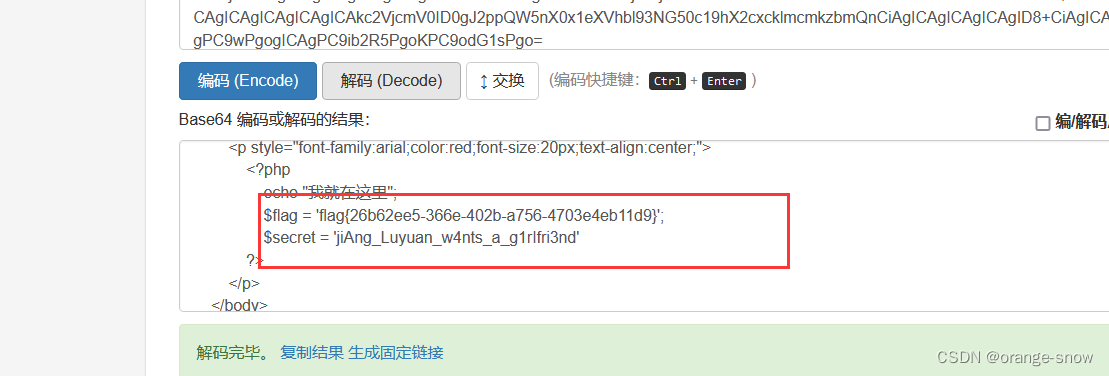
Web题记
反序列化补充知识: private变量会被序列化为:\x00类名\x00变量名 protected变量会被序列化为: \x00\*\x00变量名 public变量会被序列化为:变量名web254 这个逻辑不难,自己刚看的时候还奇怪是不是自己哪里想错了,因为…...

学习java第三十六天
Spring 官网列出的 Spring 的 6 个特征: 核心技术 :依赖注入(DI),AOP,事件(events),资源,i18n,验证,数据绑定,类型转换,SpEL。 测试 :模拟对象,…...

0205矩阵分块法-矩阵及其运算-线性代数
文章目录 1 分块矩阵的定义2 分块矩阵的运算(性质)3 按列分块与按行分块 结语 1 分块矩阵的定义 将矩阵A用若干条纵线和横线分成许多个小矩阵,每一个小矩阵称为A的子快,以子块为元素的形式上的矩阵称为分块矩阵。 2 分块矩阵的运算…...
1、java语法入门(找工作版)
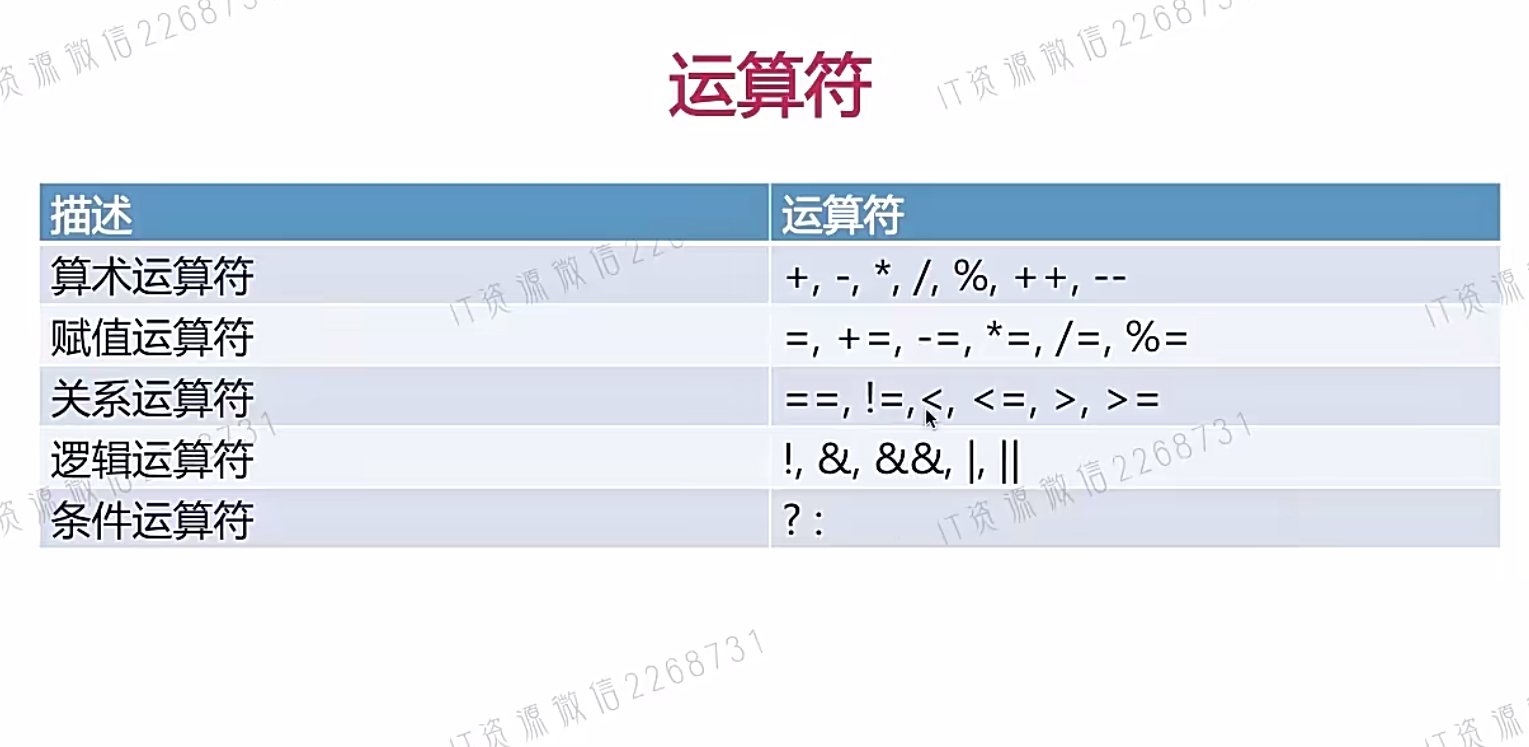
文章目录 一、Java简介二、Java常量与变量1、标识符2、关键字3、变量4、类的命名规则5、数据类型6、基本数据类型字面值7、变量的定义与初始化8、ASCII码和Unicode编码9、转义字符10、类型转换11、常量 三、Java运算符1、算术运算符2、赋值运算符3、关系运算符4、逻辑运算符5、…...

arm的状态寄存器
目录 一、arm 的 PSRs二、CPSR2.1 CPSR_cxsf 三、SPSR四、APSR 一、arm 的 PSRs arm 中有很多程序状态寄存器(Program Status Registers,PSRs)用于存储处理器的状态信息,包括 CPSR\SPSR\FPSR\APSR 等: CPSRÿ…...

2024 蓝桥打卡Day34
20240406蓝桥杯备赛 1、学习蓝桥云课省赛冲刺课 【1-手写与思维】【2-递归与递推】2、学习蓝桥云课Java省赛无忧班 【1-语言基础】3、代码练习字符串排序大小写转换 (ccfcsp之前要是学了我就能上200了 啊啊啊啊 错过啊)斐波那契数列 递归解法纸张尺寸问题…...
华为海思校园招聘-芯片-数字 IC 方向 题目分享——第九套
华为海思校园招聘-芯片-数字 IC 方向 题目分享(有参考答案)——第九套 部分题目分享,完整版获取(WX:didadidadidida313,加我备注:CSDN huawei数字芯片题目,谢绝白嫖哈) 单选 1&…...

如何创建虚拟环境打包py文件
Python 项目通常依赖于特定的库和版本。不同的项目可能依赖于相同库的不同版本,这可能导致冲突。使用虚拟环境,你可以为每个项目创建一个独立的 Python 环境,每个环境都有自己的库和版本,从而避免了依赖冲突。 采用虚拟环境打包P…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...
