java面向对象.day17(什么是面向对象)
先认识:面向过程思想,面向对象思想
面向过程思想(具体)
-
步骤清晰简单,第一步做什么,第二步做什么....
-
面对过程适合处理一些较为简单的问题
面向对象思想(抽象)
-
物以类聚,分类的思维模式,思考问题首先会解决问题需要哪些分类,然后对这些分类进行单独思考。最后,才对某个分类下的细节进行面向过程的思索。
-
面向对象适合处理复杂的问题,适合处理需要多人协作的问题!
总结:
对于描述复杂的事物,为了从宏观上把握、从整体上合理分析,我们需要使用面向对象的思路来分析整个系统。但是,具体到微观操作,仍然需要面向过程的思路去处理。
宏观方针:用--面向对象思想
微观步骤:用--面向过程思想
什么是面向对象
-
面向对象编程(Object-Oriented Programming, OOP)
-
面向对象编程的本质就是:以类的方式组织代码,以对象的组织(封装)数据。
-
抽象
-
三大特性:
-
封装
-
继承
-
多态
-
-
从认识论角度考虑是先有对象后有类。对象,是具体的事物。类,是抽象的,是对对象的抽象
-
从代码运行角度考虑是先有类后有对象。类是对象的模板。
相关文章:
)
java面向对象.day17(什么是面向对象)
先认识:面向过程思想,面向对象思想 面向过程思想(具体) 步骤清晰简单,第一步做什么,第二步做什么.... 面对过程适合处理一些较为简单的问题 面向对象思想(抽象) 物以类聚&#x…...

mysql处理并发简单示例
处理并发的基本思路是使用锁来控制对共享资源的访问。在MySQL中,可以使用事务和行级锁来处理并发。 具体处理方式如下: 创建一个用于存储并发任务的MySQL表,该表包含一个自增的ID字段和任务名称字段。设置一个最大并发数量,用来…...

顺序表——功能实现
✨✨欢迎👍👍点赞☕️☕️收藏✍✍评论 个人主页:秋邱博客 所属栏目:C语言 (感谢您的光临,您的光临蓬荜生辉) 目录 1.0 前言 2.0 线性表 2.1 顺序表 2.2 顺序表的分类 2.3 顺序表功能的实现…...

达梦导出工具dexp
基础环境 操作系统:Red Hat Enterprise Linux Server release 7.9 (Maipo) 数据库版本:DM Database Server 64 V8 架构:单实例dexp 逻辑导出 dexp 工具可以对本地或者远程数据库进行数据库级、用户级、模式级和表级的逻辑备份。备份的内容非…...

Ubuntu 22.04安装新硬盘并启动时自动挂载
方法一 要在Ubuntu 22.04系统中安装一个新硬盘、对其进行格式化并实现启动时自动挂载,需要按以下步骤操作: 1. 安装硬盘 - 确保你的硬盘正确连接到计算机上(涉及硬件安装)。 2. 发现新硬盘 - 在系统启动后,打开终端…...

Mybatis中sqlSession.getMapper背后的原理
在通过MyBatis操作数据库之前我们一定先通过Session对象获取指定Mappper接口的代理对象。如下代码所示: public class UserMapper{Select(value"SELECT * FROM user")public List<User> findAll(); }public static void main(String [] args){Conf…...

[环境配置]conda 64位安装32位python
进入32模式 set CONDA_FORCE_32BIT1创建环境 conda create --name yourEnv python3.8退出32模式 set CONDA_FORCE_32BIT0ok...

某虚假交友APP(信息窃取)逆向分析
应用初探 在群里水群的时候 群u发了一个交友APP 于是拿来分析一下 可以看到应用打开后又一个登录的界面 需要用户输入手机号与验证码进行登录 #在线云沙箱分析 将APK放入某安信云沙箱中分析 提示应用请求了过多的敏感权限 逆向分析 直接拖入Jadx分析 好在程序没有加固 也没…...
基于FPGA的按键消抖
按键工作原理 当KEY1按下时,整条电路就会导通,这个时候KEY1就是低电平; 当KEY1松开时,整条电路就会断开,这个时候KEY1就是高定平; 我们可以通过判断KEY1的高低电平来判断按键是否被按下。 为什么按键消…...
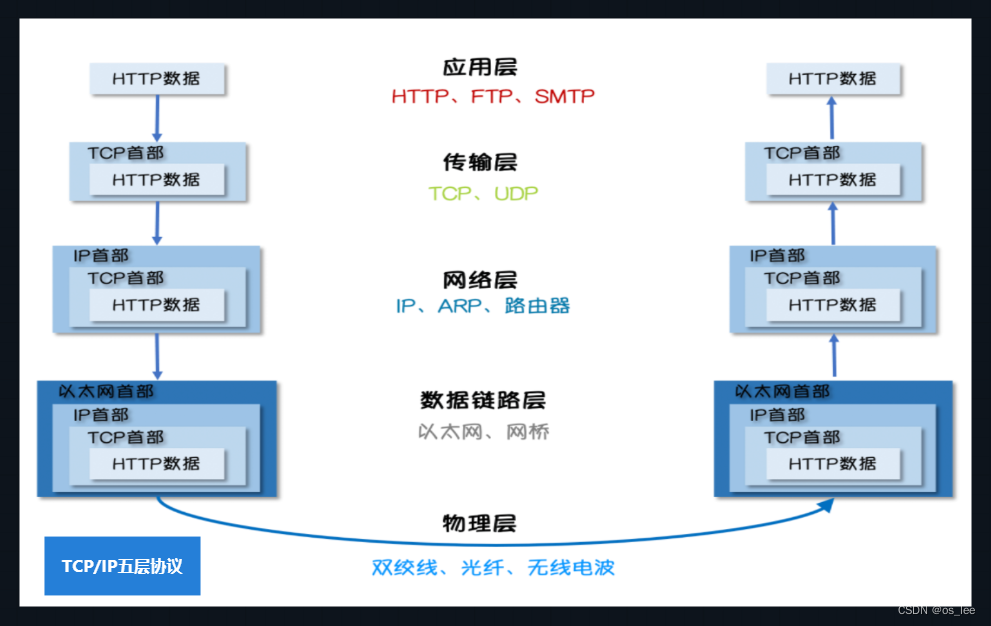
1.网络编程-网络协议
目录 网络编程是什么 网络编程三要素 OSI七层网络模型 TCP/IP五层模型 SSL/TLS 是哪层协议 网络编程是什么 网络编程是计算机科学中的一个重要领域,它涉及到编写能够在网络环境中进行通信的程序。网络编程的核心目标是使不同的设备能够通过网络交换信息&#…...
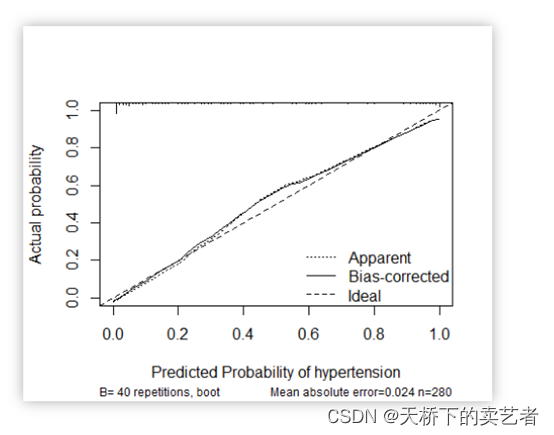
代码+视频,手动绘制logistic回归预测模型校准曲线(Calibration curve)(2)
校准曲线图表示的是预测值和实际值的差距,作为预测模型的重要部分,目前很多函数能绘制校准曲线。 一般分为两种,一种是通过Hosmer-Lemeshow检验,把P值分为10等分,求出每等分的预测值和实际值的差距 另外一种是calibrat…...
实例)
金融数据_Scikit-Learn决策树(DecisionTreeClassifier)实例
金融数据_Scikit-Learn决策树(DecisionTreeClassifier)实例 逻辑回归: 逻辑回归常被用于二分类问题, 比如涨跌预测。你可以将涨跌标记为类别, 然后使用逻辑回归进行训练。 决策树和随机森林: 决策树和随机森林是用于分类问题的强大模型。它们能够处理非线性关系, 并且对于特征…...

bash的login shell与non-login shell,以及各自的初始化过程
识别login shell与non-login shell login shell 可能是以-开头的 [almalinuxVM-AlmaLinux8-tmpl-wanlinwang ~]$ echo $0 -bash # "-" is the first character. Therefore, this is a login shell.或者以--login启动的bash [almalinuxVM-AlmaLinux8-tmpl-wanlinw…...
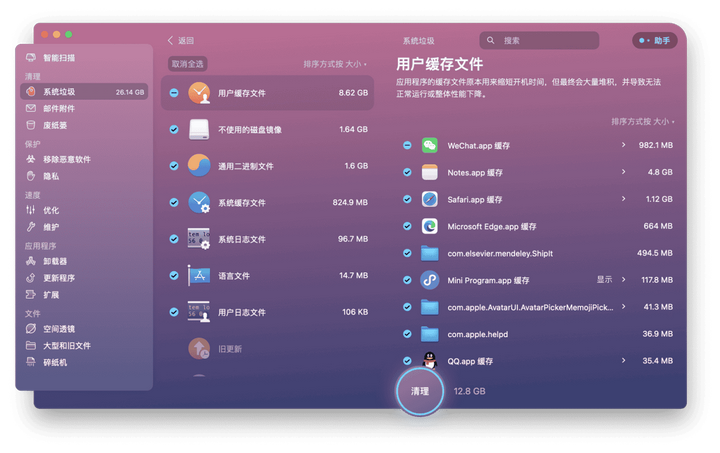
为什么苹果 Mac 电脑需要使用清理软件?
尽管 Apple Mac 电脑因其卓越的性能、简洁高效的 macOS 操作系统及独特的美学设计备受全球用户青睐,但任何电子设备在长期使用后都难以避免面临系统资源日渐累积的问题。其中一个重要维护需求在于,随着使用时间的增长,Mac电脑可能会由于系统垃…...

33. UE5 RPG使用增强输入激活GameplayAbility(三)
在前面的文章,我们实现了使用GameplayTag和InputAction的对应绑定的数据,并且添加到了增强输入映射的上下文中,实现了通过按键打印对应的GameplayTag,这只是我们基础需要制作的。目的主要是为了实现在GameplayAblity上面设置对应的…...

speech to text 库FastASR交叉编译arm target的配置
FastASR是一个比较方便的SPEECH TO TEXT的AI库。开源。下面介绍下其在交叉编译到ARM target时候的交叉编译的cmake配置: cmake_minimum_required(VERSION 3.10)project(FastASR)SET(CMAKE_C_COMPILER "/home/xxx/buildroot/output/platform_name/host/bin/aar…...
WPS快速将插入Excle数据插入Word
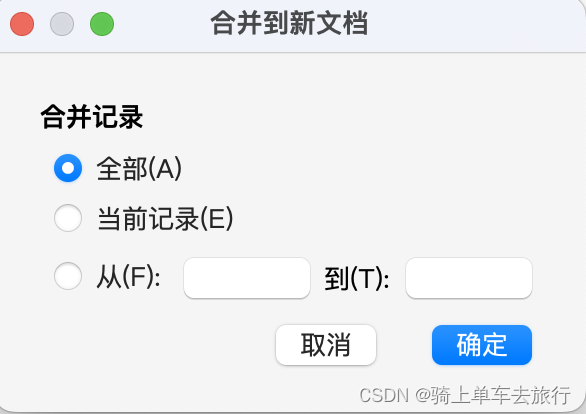
前置条件: 一张有标题、数据的excle表格word中的表格与excle表格标题对应或包含电脑已经安装WPS软件 第一步、根据word模板设计excle模板,标头对应 第二步、word上面选【引用】--【邮件】,选打开数据源,找到excle文件,…...

Springboot 集成Rabbitmq之延时队列
1.首先确保已经引入了Spring AMQP和RabbitMQ的相关依赖: <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-amqp</artifactId> </dependency> 2. 创建一个普通队列并设置TTL&#x…...

【云开发笔记NO.22】运用云原生产品打造技术中台
一、云原生产品与技术中台的结合点 云原生产品以其容器化、微服务化、自动化等特性,为技术中台的建设提供了强大的技术支持。容器化技术使得应用可以更容易地进行部署和管理,提高了应用的可移植性和弹性。微服务架构则让应用更加模块化,便于…...
C++进阶(五) 哈希
1. unordered系列关联式容器 1.1 unordered_map 1.2 unordered_map的接口说明 2. 底层结构 2.1 哈希概念 2.2 哈希冲突 2.3 哈希函数 2.4 哈希冲突解决 2.4.1 闭散列 2.4.2 开散列 3. 模拟实现 3.1 unordered_set 3.2 unordered_map 4.哈希的应用 4.1 位图 4.1.…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...
