数据挖掘|序列模式挖掘及其算法的python实现
数据挖掘|序列模式挖掘及其算法的python实现
- 1. 序列模式挖掘
- 2. 基本概念
- 3. 序列模式挖掘实例
- 4. 类Apriori算法(GSP算法)
- 4.1 算法思想
- 4.2 算法步骤
- 4.3 基于Python的算法实现
1. 序列模式挖掘
序列(sequence)模式挖掘也称为序列分析。
序列模式发现(Sequential Patterns Discovery)是由R.Agrawal于1995年首先提出的。
序列模式寻找的是事件之间在顺序上的相关性。
- 例如,“凡是买了喷墨打印机的顾客中,80%的人在三个月之后又买了墨盒”,就是一个序列关联规则。对于保险行业,通过分析顾客不同次的购买行为发现,顾客本次购买重疾险,下次购买分红保险,则企业可以通过对重疾险销量的统计来预测分红险的销售量。
序列模式挖掘在交易数据库分析、Web访问日志分析以及通信网络分析等领域具有广泛的应用前景。
2. 基本概念
设 I = i 1 , i 2 , . . . , i n I={i_1,i_2,...,i_n} I=i1,i2,...,in是一个项集,序列就是若事件(元素)组成的有序列表。
一个序列 S e Se Se可表示为 < s 1 , s 2 , . . . , s n > <s_1,s_2,...,s_n> <s1,s2,...,sn>,其中 s j ( j = 1 , 2 , … , n ) s_j(j=1,2, …, n) sj(j=1,2,…,n)为事件,也称为 S e Se Se的元素。
元素由不同的项组成。当元素只包含一项时,一般省去括号,例如, { i 2 } \{i_2\} {i2}一般表示为 i 2 i_2 i2。
元素之间是有顺序的,但元素内的项是无序的,一般定义为词典序。序列包含项的个数称为序列的长度,长度为 L L L的序列记为 L − 序列 L-序列 L−序列。
序列数据库就是元组 < s i d , S e > <sid, Se> <sid,Se>的集合,即有序事件序列组成的数据库,其中 S e Se Se是序列, s i d sid sid 是该序列的序列号。
存在两个序列 α = < a 1 , a 2 , . . . , a n > , β = < b 1 , b 2 , … , b n > \alpha = <a_1, a_2, ...,a_n>, \beta = <b_1, b_2, …, b_n> α=<a1,a2,...,an>,β=<b1,b2,…,bn>,如果存在整数 1 ≤ i 1 < i 2 < … < i n ≤ m 1\leq i_1 < i_2 <…<i_n \leq m 1≤i1<i2<…<in≤m 且 a 1 ⊆ b i 1 , a 2 ⊆ b i 2 , … , a n ⊆ b i n a_1\subseteq b_{i1}, a_2 \subseteq b_{i2}, …, a_n \subseteq b_{in} a1⊆bi1,a2⊆bi2,…,an⊆bin,那么称序列 α \alpha α是 β \beta β 的子序列(subsequence),或者序列 β \beta β 包含 α \alpha α,记作 α ⊆ β \alpha\subseteq \beta α⊆β 。
序列在序列数据库 S e Se Se 中的支持度为序列数据库 S e Se Se 中包含序列 α \alpha α的序列个数除以总的序列数,记为 s u p p o r t ( α ) support (\alpha) support(α)。给定支持度阈值 τ \tau τ,如果序列 α \alpha α在序列数据库中的支持度不低于 τ \tau τ,则称序列 α \alpha α为序列模式(频繁序列)。
3. 序列模式挖掘实例
现有事务数据库如下表1所示,交易中不考虑顾客购买物品的数量,只考虑物品有没有被购买。整理后可得到顾客购物序列库,如表2所示。
- 表1:顾客购物事务数据库
| 时间 | 顾客ID | 购物项集 |
|---|---|---|
| 2023.12.10 | 2 | 10,20 |
| 2023.12.11 | 5 | 90 |
| 2023.12.12 | 2 | 30 |
| 2023.12.13 | 2 | 40,60,70 |
| 2023.12.14 | 4 | 30 |
| 2023.12.15 | 3 | 30,50,70 |
| 2023.12.17 | 1 | 30 |
| 2023.12.17 | 1 | 90 |
| 2023.12.18 | 4 | 40,70 |
| 2023.12.19 | 4 | 90 |
- 表2:顾客购物序列库
| 顾客ID | 顾客购物序列 |
|---|---|
| 1 | <30,90> |
| 2 | <{10,20},30,{40,60,70}> |
| 3 | <{30,50,70}> |
| 4 | <30,{40,70},90> |
| 5 | <90> |
设最小支持度为 25%,从表2中可以看出,<30,90> 是 <30, {40,70},90> 的子序列。两个序列<30,90>、<30,{40,70},90>的支持度都为 40%,因此是序列模式。
4. 类Apriori算法(GSP算法)
序列模式挖掘是在给定序列数据库中找出满足最小支持度阈值的序列模式的过程。
4.1 算法思想
采用分而治之的思想,不断产生序列数据库的多个更小的投影数据库,然后在各个投影数据库上进行序列模式挖掘。
4.2 算法步骤
- 扫描序列数据库,得到长度为 1 1 1的序列模式 L 1 L1 L1,作为初始的种子集。
- 根据长度为 i i i 的种子集 L i ( i ≥ 1 ) L_i (i\geq1) Li(i≥1) 通过连接操作生成长度为 i + 1 i+1 i+1的候选序列模式 C i + 1 C_{i+1} Ci+1;然后扫描序列数据库,计算每个候选序列模式的支持数,产生长度为 i + 1 i+1 i+1的序列模式 L i + 1 L_{i+1} Li+1,并将 L i + 1 L_{i+1} Li+1 作为新的种子集。
- 重复第二步,直到没有新的序列模式或新的候选序列模式产生为止
4.3 基于Python的算法实现
问题:原始序列为:<1,2,3,4>,<{1,5},2,3,4>, <1,3,4,{3,5}>, <1,3,5>, <4,5>,挖掘其中的序列模式。
以下代码是本人自己实现的。感觉原始序列的数据结构使用的不太好,导致子模式识别较为麻烦,可能存在错误,仅保证本算例正确,敬请谅解。
import numpy as np
#子模式判断
def isSubSeq(seq,subseq)->bool:i=0;if len(subseq)>len(seq):return Falsefor sel in subseq:if i >= len(seq):return Falsefor j in range(i,len(seq)):if type(seq[j])==list:if sel in seq[j]:i=j+1breakelif j==len(seq)-1:return Falseelif sel==seq[j]:i=j+1breakelif j==len(seq)-1:return Falseelse:continuereturn True # 获取L1数据集
def getL1(seq):ds=[]for ss in seq:for s in ss:if type(s)==list:for e in s:if [e] not in ds:ds.append([e])else:if [s] not in ds:ds.append([s])return np.array(ds)# 获取L2数据集
def getL2(l1seq)->np.ndarray:ds=[]for i in range(len(l1seq)):for j in range(len(l1seq)):if i != j:#np.append(ds, [l1seq[i],l1seq[j]])ds.append([l1seq[i][0],l1seq[j][0]]) return np.array(ds) # 获取L3数据集
def getL3(l1seq,l2seq):ds=[]for se2 in l2seq:for se1 in l1seq:if se1 not in se2:ds.append(np.append(se2, se1)) return ds
# 获取L4数据集
def getL4(l1seq,l3seq):ds=[]for se3 in l3seq:for se1 in l1seq:if se1 not in se3:ds.append(np.append(se3, se1)) return ds #计算支持度
def calSup(dsq,seq):i=0.0for s in dsq:if isSubSeq(s,seq):i=i+1return i/len(dsq)if __name__ == "__main__":min_support = 0.4 #最小支持度dsq = np.array([[1,2,3,4],[[1,5],2,3,4],[1,3,4,[3,5]],[1,3,5],[4,5]],dtype=object)l1=getL1(dsq)for l in l1:print('序列-1:',l,'的支持度为:',calSup(dsq, l))l2 = getL2(l1)l2seq=[]for i in range(len(l2)):sups=calSup(dsq, l2[i])if sups >=min_support:print('序列-2:',l2[i],'的支持度为:',sups)l2seq.append(l2[i])l3=getL3(l1,l2seq)l3seq=[]for i in range(len(l3)):sups=calSup(dsq, l3[i])if sups >=min_support:print('序列-3:',l3[i],'的支持度为:',sups)l3seq.append(l3[i])l4=getL4(l1,l3seq)l4seq=[]for i in range(len(l4)):sups=calSup(dsq, l4[i])if sups >=min_support:print('序列-4:',l4[i],'的支持度为:',sups)l4seq.append(l4[i])
输出:
序列-1: [1] 的支持度为: 0.8序列-1: [2] 的支持度为: 0.4序列-1: [3] 的支持度为: 0.8序列-1: [4] 的支持度为: 0.8序列-1: [5] 的支持度为: 0.8序列-2: [1 2] 的支持度为: 0.4序列-2: [1 3] 的支持度为: 0.8序列-2: [1 4] 的支持度为: 0.6序列-2: [1 5] 的支持度为: 0.4序列-2: [2 3] 的支持度为: 0.4序列-2: [2 4] 的支持度为: 0.4序列-2: [3 4] 的支持度为: 0.6序列-2: [3 5] 的支持度为: 0.4序列-2: [4 5] 的支持度为: 0.4序列-3: [1 2 3] 的支持度为: 0.4序列-3: [1 2 4] 的支持度为: 0.4序列-3: [1 3 4] 的支持度为: 0.6序列-3: [1 3 5] 的支持度为: 0.4序列-3: [2 3 4] 的支持度为: 0.4序列-4: [1 2 3 4] 的支持度为: 0.4
相关文章:

数据挖掘|序列模式挖掘及其算法的python实现
数据挖掘|序列模式挖掘及其算法的python实现 1. 序列模式挖掘2. 基本概念3. 序列模式挖掘实例4. 类Apriori算法(GSP算法)4.1 算法思想4.2 算法步骤4.3 基于Python的算法实现 1. 序列模式挖掘 序列(sequence)模式挖掘也称为序列分析。 序列模式发现&…...
3. Django 初探路由
3. 初探路由 一个完整的路由包含: 路由地址, 视图函数(或者视图类), 可选变量和路由命名. 本章讲述Django的路由编写规则与使用方法, 内容分为: 路由定义规则, 命名空间与路由命名, 路由的使用方式.3.1 路由定义规则 路由称为URL (Uniform Resource Locator, 统一资源定位符)…...
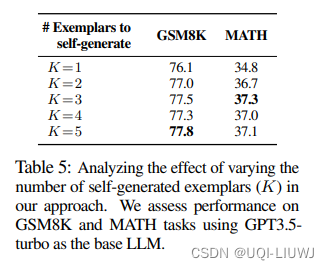
论文笔记:Large Language Models as Analogical Reasoners
iclr 2024 reviewer打分5558 1 intro 基于CoT prompt的大模型能够更好地解决复杂推理问题 然而传统CoT需要提供相关的例子作为指导,这就增加了人工标注的成本——>Zero-shot CoT避免了人工标注来引导推理 但是对于一些复杂的任务难以完成推理,例如c…...

第3章 数据定义语言DDL
文章目录 第3章 DDL语言:数据定义语言3.1 MySQL的数据类型3.2 表的创建:create3.3 表的删除:drop3.4 快速创建表3.5 快速删除表中的数据:truncate3.6 修改表结构:alter 第5章 约束5.1 非空约束:not null5.2…...
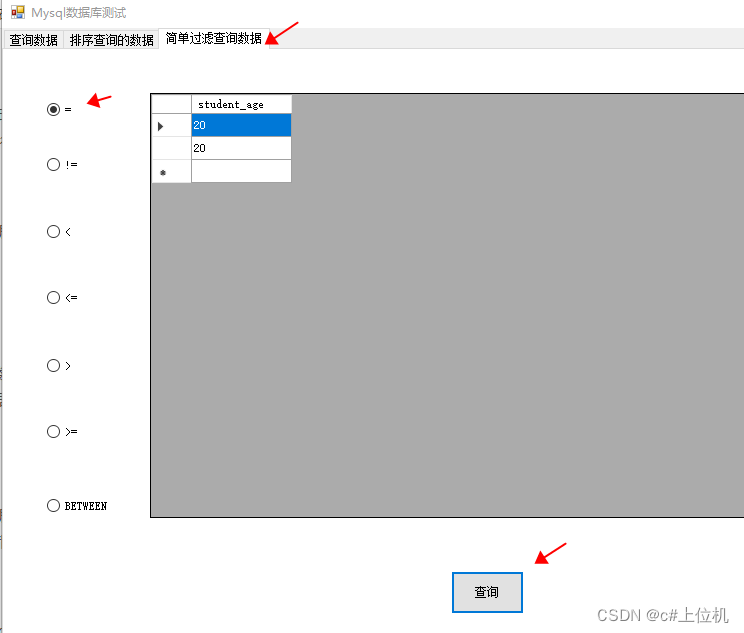
C#操作MySQL从入门到精通(7)——对查询数据进行简单过滤
前言 我们在查询数据库中数据的时候,有时候需要剔除一些我们不想要的数据,这时候就需要对数据进行过滤,比如学生信息中,我只需要年龄等于18的,类似这种操作,本文就是详细介绍如何对查询的数据进行初步的过滤。 1、等于操作符 本次查询student_age 等于20的数据,使用我…...
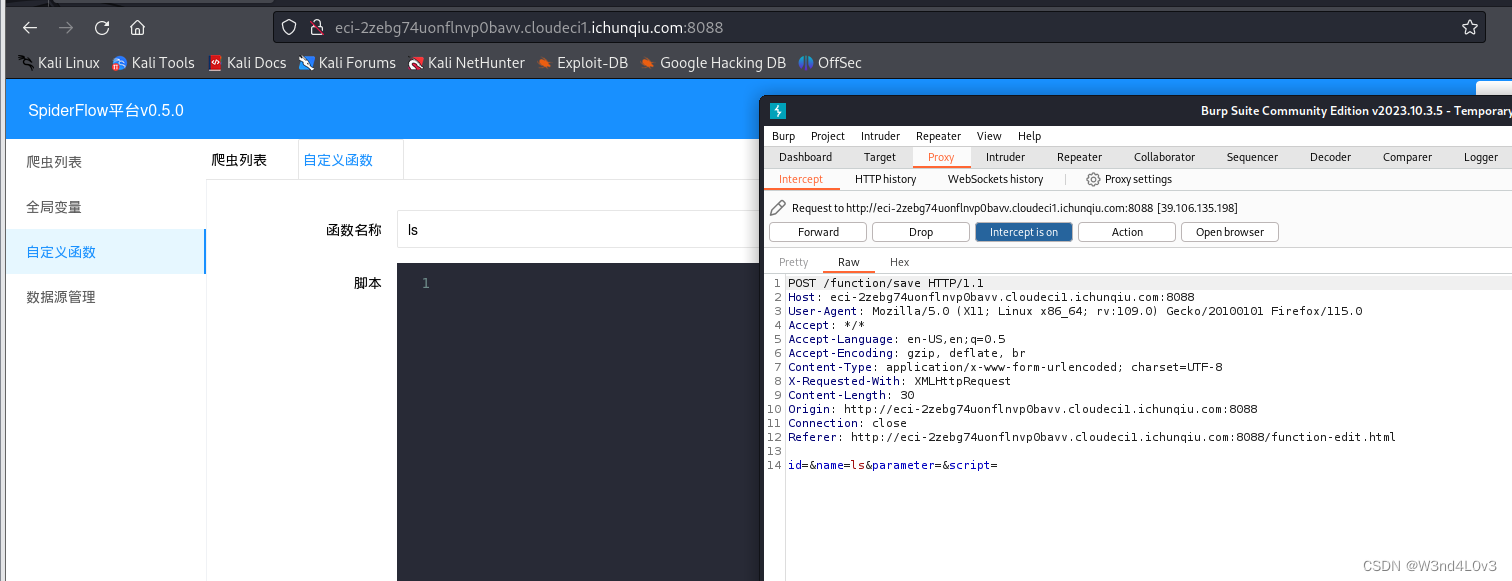
【CVE复现计划】CVE-2024-0195
CVE-2024-0195 简介: SpiderFlow是新一代开源爬虫平台,以图形化方式定义爬虫流程,不写代码即可完成爬虫。基于springbootlayui开发的前后端不分离,也可以进行二次开发。该系统/function/save接口存在RCE漏洞,攻击者可以构造恶意命…...
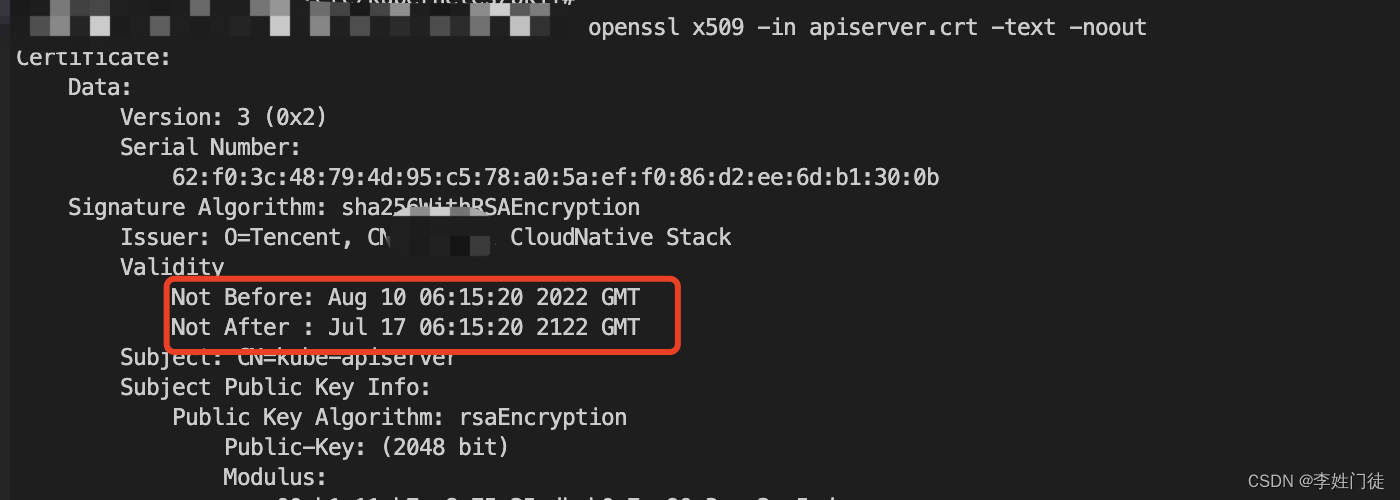
k8s的ca以及相关证书签发流程
k8s的ca以及相关证书签发流程 1. kube-apiserver相关证书说明2. 生成CA凭证1.1. 生成CA私钥1.2. 生成CA证书 2. 生成kube-apiserver凭证2.1. 生成kube-apiserver私钥2.2. 生成kube-apiserver证书请求2.3. 生成kube-apiserver证书 3. 疑问和思考4. 参考文档 对于网站类的应用&am…...

思迈特软件与上海德拓签署战略合作协议,携手赋能企业数字化转型
3月27日,广州思迈特软件有限公司(简称“思迈特软件”)与上海德拓信息技术有限公司(简称“德拓信息”)正式签约建立战略合作伙伴关系。双方将在数字化转型、数据服务、数据应用以及市场资源等多个领域展开深度合作&…...

【快捷部署】015_Minio(latest)
📣【快捷部署系列】015期信息 编号选型版本操作系统部署形式部署模式复检时间015MiniolatestCentOS 7.XDocker单机2024-04-09 一、快捷部署 #!/bin/bash ################################################################################# # 作者:c…...

<网络安全>《72 微课堂<什么是靶场?>》
1 简介 网络安全靶场是一种模拟真实网络环境的技术或平台。 网络安全靶场基于虚拟化技术,能够模拟网络架构、系统设备、业务流程的运行状态及运行环境,用于支持网络安全相关的学习、研究、检验、竞赛和演习等活动,旨在提高人员及机构的网络…...

Golang | Leetcode Golang题解之第18题四数之和
题目: 题解: func fourSum(nums []int, target int) (quadruplets [][]int) {sort.Ints(nums)n : len(nums)for i : 0; i < n-3 && nums[i]nums[i1]nums[i2]nums[i3] < target; i {if i > 0 && nums[i] nums[i-1] || nums[i]…...

自动驾驶中的传感器融合算法:卡尔曼滤波器和扩展卡尔曼滤波器
自动驾驶中的传感器融合算法:卡尔曼滤波器和扩展卡尔曼滤波器 附赠自动驾驶学习资料和量产经验:链接 介绍: 追踪静止和移动的目标是自动驾驶技术领域最为需要的核心技术之一。来源于多种传感器的信号,包括摄像头,雷达…...
基于ssm的星空游戏购买下载平台的设计与实现论文
摘 要 随着科学技术的飞速发展,各行各业都在努力与现代先进技术接轨,通过科技手段提高自身的优势,商品交易当然也不能排除在外,随着商品交易管理的不断成熟,它彻底改变了过去传统的经营管理方式,不仅使商品…...

DSOX6004A是德科技DSOX6004A示波器
181/2461/8938产品概述: 特点: 是德科技DSOX6004A具有7合1集成功能,结合了数字通道、串行协议分析、内置双通道波形发生器、频率响应分析、内置数字万用表和带累加器的内置10位计数器。1千兆赫至6千兆赫4个模拟通道在12.1英寸电容式多点触摸屏上轻松查…...

golang 使用 cipher、aes 实现 oauth2 验证
在Go语言中,crypto/cipher包提供了加密和解密消息的功能。这个包实现了各种加密算法,如AES、DES、3DES、RC4等,以及相应的模式,如ECB、CBC、CFB、OFB、CTR等。以下是如何使用crypto/cipher包进行加密和解密操作的基本步骤…...
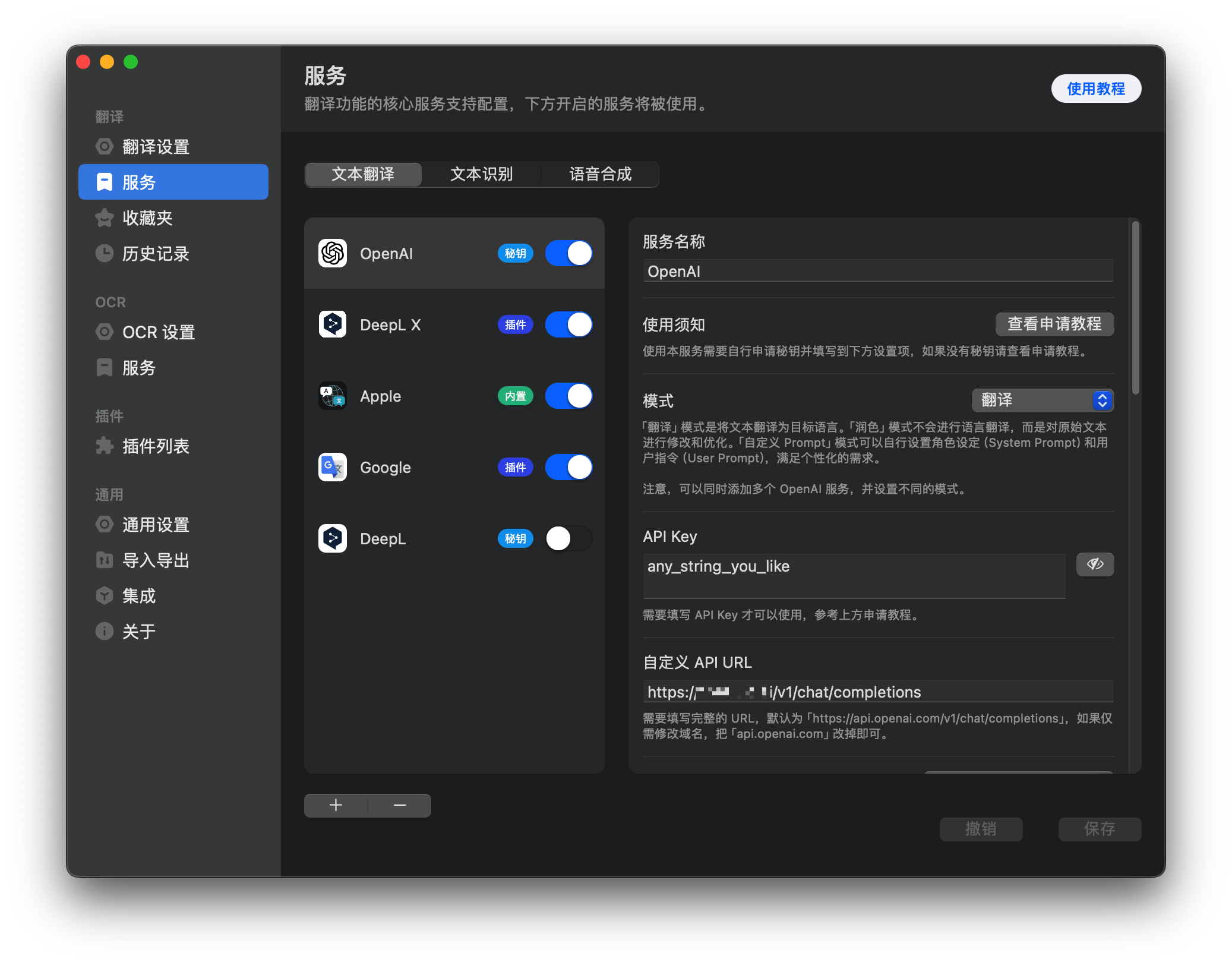
LLMs之FreeGPT35:FreeGPT35的简介、安装和使用方法、案例应用之详细攻略
LLMs之FreeGPT35:FreeGPT35的简介、安装和使用方法、案例应用之详细攻略 目录 FreeGPT35的简介 FreeGPT35的安装和使用方法 1、部署和启动服务 Node 2、使用 Docker 部署服务: 运行 Docker 容器以部署服务 使用 Docker Compose 进行更方便的容器化…...

【力扣一刷】代码随想录day32(贪心算法part2:122.买卖股票的最佳时机II、55. 跳跃游戏、45.跳跃游戏II )
目录 【122.买卖股票的最佳时机II】中等题 方法一 贪心算法 方法二 动态规划 【55. 跳跃游戏】中等题 【尝试】 递归 (超时) 方法 贪心算法 【45.跳跃游戏II】中等题 方法 贪心算法 【122.买卖股票的最佳时机II】中等题(偏简单࿰…...
安卓远离手机app
软件介绍 远离手机是专门为防止年轻人上瘾而打造的生活管理类的软件,适度用手机,保护眼睛,节约时间。 下载 安卓远离手机app...
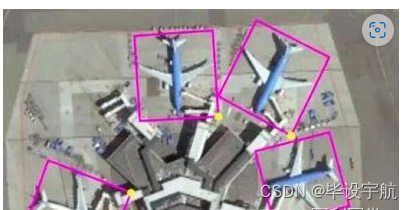
yolov5旋转目标检测遥感图像检测-无人机旋转目标检测(代码和原理)
YOLOv5(You Only Look Once version 5)是一个流行且高效的实时目标检测深度学习模型,最初设计用于处理图像中的水平矩形边界框目标。然而,对于旋转目标检测,通常需要对原始YOLOv5架构进行扩展或修改,以便能…...

云手机提供私域流量变现方案
当今数字营销领域,私域流量是一座巨大的金矿,然而并非人人能够轻易挖掘。一家营销公司面临着利用社交、社区、自媒体等应用积累私域流量,并通过销售产品、推送广告等方式实现流量变现的挑战与困境。本文将详细介绍这家公司是如何通过云手机&a…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...
