贪心算法|135.分发糖果
力扣题目链接
class Solution {
public:int candy(vector<int>& ratings) {vector<int> candyVec(ratings.size(), 1);// 从前向后for (int i = 1; i < ratings.size(); i++) {if (ratings[i] > ratings[i - 1]) candyVec[i] = candyVec[i - 1] + 1;}// 从后向前for (int i = ratings.size() - 2; i >= 0; i--) {if (ratings[i] > ratings[i + 1] ) {candyVec[i] = max(candyVec[i], candyVec[i + 1] + 1);}}// 统计结果int result = 0;for (int i = 0; i < candyVec.size(); i++) result += candyVec[i];return result;}
};看着是困难题,其实仔细理解并不是很吓人。
这题的重点在如何遍历。
vector<int> candyVec(ratings.size(), 1); 还有它是个啥?
vector < int > myVector(num); 或者 vector < int > myVector(n,num);
类似于resize的用法
函数原型:
void resize (size_type n);
void resize (size_type n, const value_type& val);
作用:
改变容器的大小,使得其包含n个元素。常见三种用法。1、如果n小于当前的容器大小,那么则保留容器的前n个元素,去除(erasing)超过的部分。
2、如果n大于当前的容器大小,则通过在容器结尾插入(inserting)适合数量的元素使得整个容器大小达到n。且如果给出val,插入的新元素全为val,否则,执行默认构造函数。
3、如果n大于当前容器的容量(capacity)时,则会自动重新分配一个存储空间。
注意:如果发生了重新分配,则使用容器的分配器分配存储空间,这可能会在失败时抛出异常。
思路
这道题目一定是要确定一边之后,再确定另一边,例如比较每一个孩子的左边,然后再比较右边,如果两边一起考虑一定会顾此失彼。
先确定右边评分大于左边的情况(也就是从前向后遍历)
此时局部最优:只要右边评分比左边大,右边的孩子就多一个糖果,全局最优:相邻的孩子中,评分高的右孩子获得比左边孩子更多的糖果
局部最优可以推出全局最优。
如果ratings[i] > ratings[i - 1] 那么[i]的糖 一定要比[i - 1]的糖多一个,所以贪心:candyVec[i] = candyVec[i - 1] + 1
代码如下:
// 从前向后
for (int i = 1; i < ratings.size(); i++) {if (ratings[i] > ratings[i - 1]) candyVec[i] = candyVec[i - 1] + 1;
}
如图:
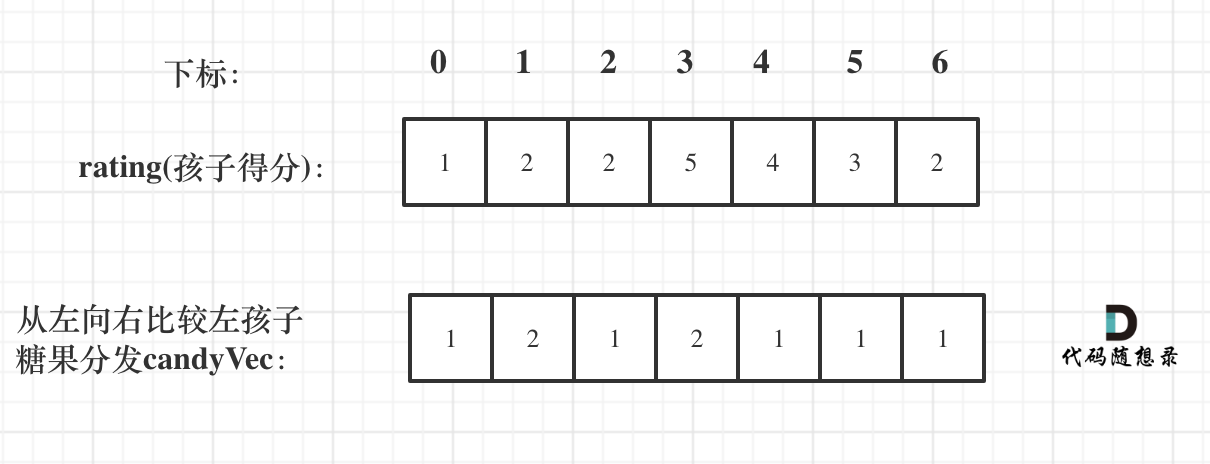
再确定左孩子大于右孩子的情况(从后向前遍历)
遍历顺序这里有同学可能会有疑问,为什么不能从前向后遍历呢?
因为 rating[5]与rating[4]的比较 要利用上 rating[5]与rating[6]的比较结果,所以 要从后向前遍历。
如果从前向后遍历,rating[5]与rating[4]的比较 就不能用上 rating[5]与rating[6]的比较结果了 。如图:

所以确定左孩子大于右孩子的情况一定要从后向前遍历!
如果 ratings[i] > ratings[i + 1],此时candyVec[i](第i个小孩的糖果数量)就有两个选择了,一个是candyVec[i + 1] + 1(从右边这个加1得到的糖果数量),一个是candyVec[i](之前比较右孩子大于左孩子得到的糖果数量)。
那么又要贪心了,局部最优:取candyVec[i + 1] + 1 和 candyVec[i] 最大的糖果数量,保证第i个小孩的糖果数量既大于左边的也大于右边的。全局最优:相邻的孩子中,评分高的孩子获得更多的糖果。
局部最优可以推出全局最优。
所以就取candyVec[i + 1] + 1 和 candyVec[i] 最大的糖果数量,candyVec[i]只有取最大的才能既保持对左边candyVec[i - 1]的糖果多,也比右边candyVec[i + 1]的糖果多。
如图:
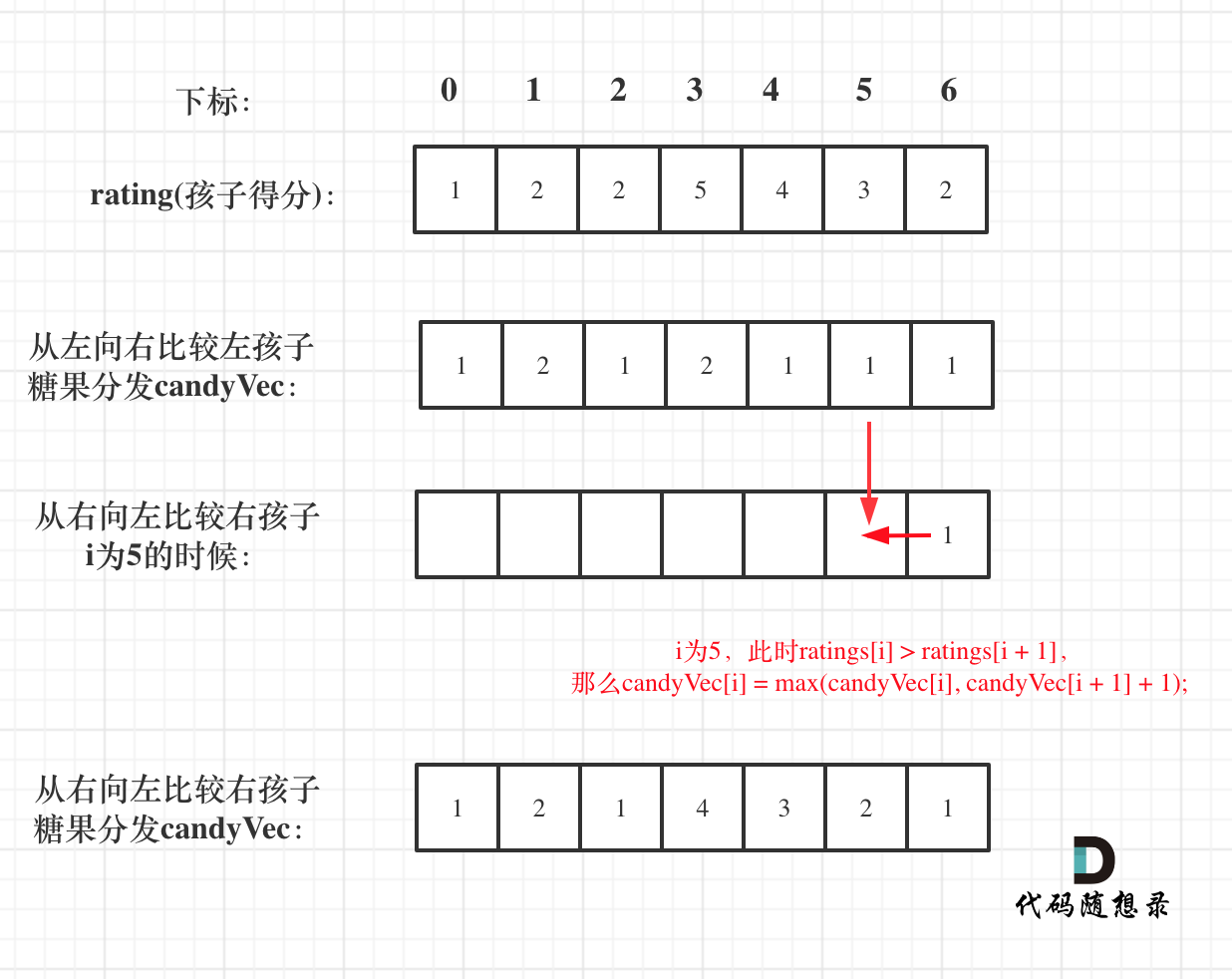
所以该过程代码如下:
// 从后向前
for (int i = ratings.size() - 2; i >= 0; i--) {if (ratings[i] > ratings[i + 1] ) {candyVec[i] = max(candyVec[i], candyVec[i + 1] + 1);}
}自己的思路:
其实我没太搞懂这个遍历的意思,但是知道只能从一边开始看
好吧,我承认这题还是有点难的,一直没搞清楚从前向后和从后向前什么意思啊!!!
相关文章:

贪心算法|135.分发糖果
力扣题目链接 class Solution { public:int candy(vector<int>& ratings) {vector<int> candyVec(ratings.size(), 1);// 从前向后for (int i 1; i < ratings.size(); i) {if (ratings[i] > ratings[i - 1]) candyVec[i] candyVec[i - 1] 1;}// 从后…...
c# wpf template itemtemplate+ListBox
1.概要 2.代码 <Window x:Class"WpfApp2.Window7"xmlns"http://schemas.microsoft.com/winfx/2006/xaml/presentation"xmlns:x"http://schemas.microsoft.com/winfx/2006/xaml"xmlns:d"http://schemas.microsoft.com/expression/blend/…...
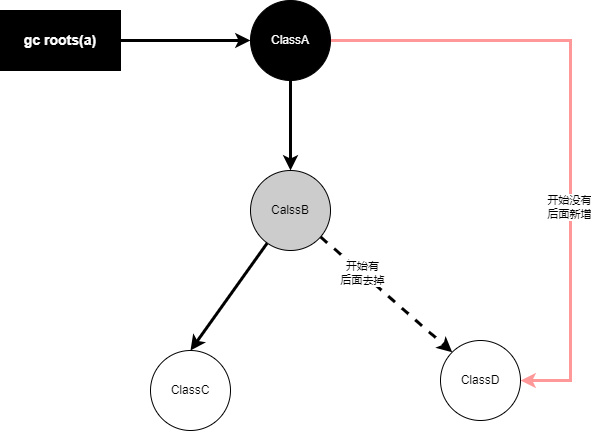
关于JVM-三色标记算法剖析
相关系列 深入理解JVM垃圾收集器-CSDN博客 深入理解JVM垃圾收集算法-CSDN博客 深入理解jvm执行引擎-CSDN博客 jvm优化原则-CSDN博客 jvm流程图-CSDN博客 三色标记产生的原因? 在并发标记的过程中,因为标记期间应用线程还在继续跑,对象间的引…...
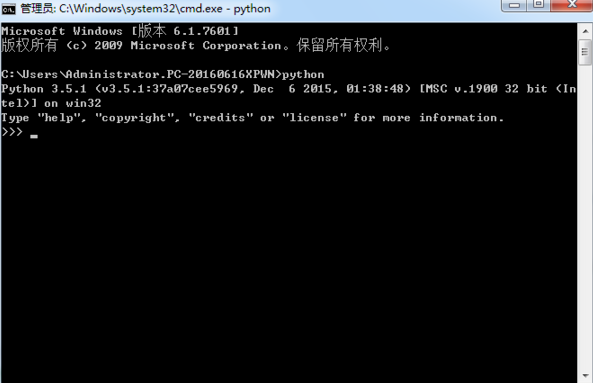
怎么看有没有装python
windows系统,运行——cmd,进入dos窗口,输入python,安装成功的话可以看到版本信息并进入编程模式。 如下图(我安装的版本是python 3.5.1):...

VS CODE环境安装和hello world
SAP UI5 demo walkthrough tutorial step1 hello word 首先要安装nodejs,然后才能执行下面的操作 nodejs vscode 安装ui5 npm install --global ui5/cli报错解决: idealTree:npm: sill idealTree buildDeps 这个信息说明npm正在构建,如一直停留在这个…...

mysql性能索引调优易混点总结
文章目录 一、 前言二、explain相关三、索引优化相关联合索引索引下推排序和分组相关优化分页优化表关联优化嵌套循环连接 Nested-Loop Join(NLJ) 算法in和exsits优化 一、 前言 近几年看了很多和mysql相关的书,文章或视频,但仍然有一些点,看…...

区块链与数字身份:探索Facebook的新尝试
在数字化时代,随着区块链技术的崛起,数字身份成为了一个备受关注的话题。作为全球最大的社交媒体平台之一,Facebook一直在探索如何利用区块链技术来改善数字身份管理和用户数据安全。本文将深入探讨Facebook在这一领域的新尝试,探…...
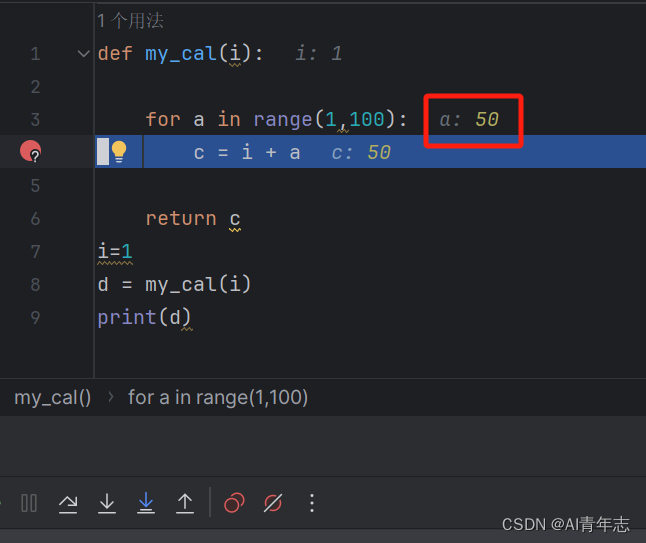
【pycharm】在debug循环时,如何快速debug到指定循环次数
【pycharm】在debug循环时,如何快速debug到指定循环次数 【先赞后看养成习惯】求关注收藏点赞😀 在 PyCharm 中,可以使用条件断点来实现在特定循环次数后停止调试。这可以通过在断点处右键单击,然后选择 “Add Breakpoint” -&g…...

【蓝桥杯每日一题】4.8 公约数
题目来源: 4199. 公约数 - AcWing题库 问题描述: 找到最大整数x,需满足下面两个条件 x x x是 a a a, b b b的公约数 l < x < r l<x<r l<x<r 思路: 找到 a a a, b b b两个数的最大公约数 g c g c d (…...

【MySQL学习】MySQL的慢查询日志和错误日志
꒰˃͈꒵˂͈꒱ write in front ꒰˃͈꒵˂͈꒱ ʕ̯•͡˔•̯᷅ʔ大家好,我是xiaoxie.希望你看完之后,有不足之处请多多谅解,让我们一起共同进步૮₍❀ᴗ͈ . ᴗ͈ აxiaoxieʕ̯•͡˔•̯᷅ʔ—CSDN博客 本文由xiaoxieʕ̯•͡˔•̯᷅ʔ 原创 CSDN …...

# C++之functional库用法整理
C之functional库用法整理 注:整理一些突然学到的C知识,随时mark一下 例如:忘记的关键字用法,新关键字,新数据结构 C 的function库用法整理 C之functional库用法整理一、functional库的内建仿函数1. 存储和调用函数2. 存…...
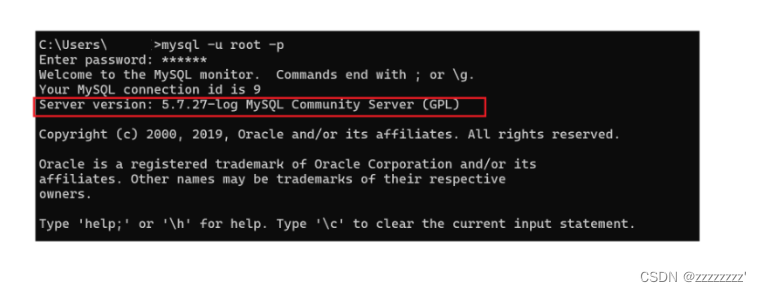
查看MySQL版本的方式
文章目录 一、使用cmd输入命令行查看二、在mysql客户端服务器里查询 一、使用cmd输入命令行查看 1、打开 cmd ,输入命令行: mysql --version 2、还是打开cmd,输入命令行:mysql -V (注意了,此时的V是个大写的V) 二、…...

k8s_入门_命令详解
命令详解 kubectl是官方的CLI命令行工具,用于与 apiserver进行通信,将用户在命令行输入的命令,组织并转化为 apiserver能识别的信息,进而实现管理k8s各种资源的一种有效途径 1. 帮助 2. 查看版本信息 3. 查看资源对象等 查看No…...

腾讯、阿里、字节….等大厂都更喜欢什么样的简历?
我985毕业,为什么筛选简历时输给了一个普通一本? 我投了20份简历,为什么没有一个大厂回我? 每次HR收到简历就没下文了,是我的简历有问题吗? 诚然,在求职时,简历往往就是我们给予H…...

OpenHarmony实战:帆移植案例(中)
OpenHarmony实战:帆移植案例(上) Audio服务介绍 服务节点 基于ADM框架的audio驱动对HDI层提供三个服务hdf_audio_render、hdf_audio_capture、hdf_audio_control。 开发板audio驱动服务节点如下: console:/dev # ls -al hdf_au…...

武汉星起航:创始人张振邦智慧领航,孵化伙伴共绘跨境新蓝图!
在风起云涌的跨境电商行业中,武汉星起航电子商务有限公司如同一颗璀璨的明星,引领着众多创业者迈向成功的彼岸。而这一切的背后,都离不开公司创始人张振邦先生的卓越领导与深厚经验。他凭借着在电子商务行业多年的深耕与积累,为武…...

上下收缩、折叠面板
效果: 上下收缩、折叠面板,类似QQ好友列表那种。原理就是在一个布局中,通过button来实现一个独立widget的visible/disable 实现: 1.分组按钮 #ifndef EXPANDPANEL_H #define EXPANDPANEL_H#include <QWidget>class…...

XC7A35T-2FGG484 嵌入式FPGA现场可编程门阵列 Xilinx
XC7A35T-2FGG484 是一款由Xilinx(赛灵思)制造的FPGA(现场可编程门阵列)芯片 以下是XC7A35T-2FGG484 的主要参数: 1. 系列:Artix-7 2. 逻辑单元数量:33280个 3. 工艺技术:28nm 4. …...

淘宝订单API接口:电商业务自动化的新选择
淘宝订单API接口在电商业务自动化中扮演了至关重要的角色。首先,通过API接口,商家可以自动化地查询、创建、修改和删除订单,极大地提高了订单处理效率,减少了人工操作,降低了错误率。其次,商家可以实时获取…...

识典百科词条创建技巧,教你如何轻松创建热门识典百科词条!
网络已经成为人们获取知识和信息的主要途径。在这样一个背景下,识典百科作为一个综合性的网络百科全书,在为读者们提供各种知识的同时,也给广大用户提供了一个创建、编辑和分享知识的平台。如何在识典百科上创建一个高质量的词条,…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...
