C++手撕红黑树
文章目录
- 红黑树
- 概念
- 性质(条件限制)
- 节点的定义
- 红黑树的结构
- 红黑树的插入
- cur为红,p为红,g为黑,u存在且为红
- cur为红,p为红,g为黑,u不存在或u为黑,插入到p对应的一边
- cur为红,p为红,g为黑,u不存在或u存在且为黑,插入到与p相反的一边
- 示例代码
- 红黑树的验证
- 红黑树与AVL树的比较
- 完整代码
红黑树
概念
和AVL树一样,红黑树也是一种二叉搜索树,是解决二叉搜索树不平衡的另一种方案,他在每个节点上增加一个存储位,用于表示节点的颜色,是Red或者Black
红黑树的核心思想是通过一些着色的条件限制,达到一种最长路径不超过最短路径的两倍的状态
所以说红黑树并不是严格平衡的树,而是一种近似平衡
例如
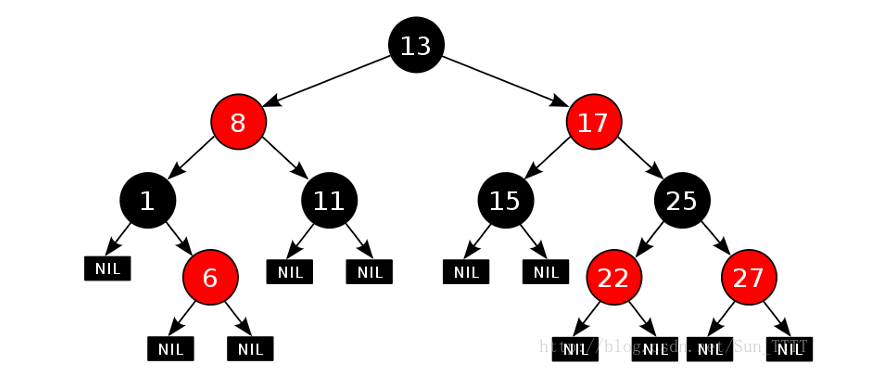
性质(条件限制)
红黑树一共有五条性质,由此来保证最长路径不超过最短路径的两倍
- 每个节点都有颜色,不是黑色就是红色
- 根节点是黑色的
- 如果一共节点是红色,那么他的子节点一定是黑色(不会出现两个红色节点连接的情况)
- 对于每个节点,以这个节点到所有后代的任意路径上,均包含相同数目的黑色节点
- 每个叶子节点(空节点)是黑色的(为了满足第四条性质,某些情况下如果没有第五条第四条会失效)
节点的定义
// 颜色
enum Color {RED,BLACK
};template<class T>
struct RBTreeNode {RBTreeNode<T>* _left;RBTreeNode<T>* _right;RBTreeNode<T>* _parent;T _data;Color _col;RBTreeNode(const T& data) :_left(nullptr),_right(nullptr),_parent(nullptr),_data(data),_col(RED){}
};
我们定义颜色时,使用枚举类型,可以方便且明了的看到颜色
除此之外我们默认插入节点是红色的,因为一旦插入节点是黑色,就会违反第四条规则,如果要满足的话,就要走到每一条路径上插入对应的黑色节点,代价巨大
当插入节点是红色时,有可能会违反第三条规则,但是我们可以通过变色,旋转等操作在局部进行改变,这样就能使之仍然满足条件
红黑树的结构
为了后续利用红黑树封装map和set,我们对红黑树增加一个头节点,为了和根节点进行区分,我们将头节点赋为黑色,并且让头节点的parent指向根节点,left指向红黑树的最小节点,right指向最大节点,如图
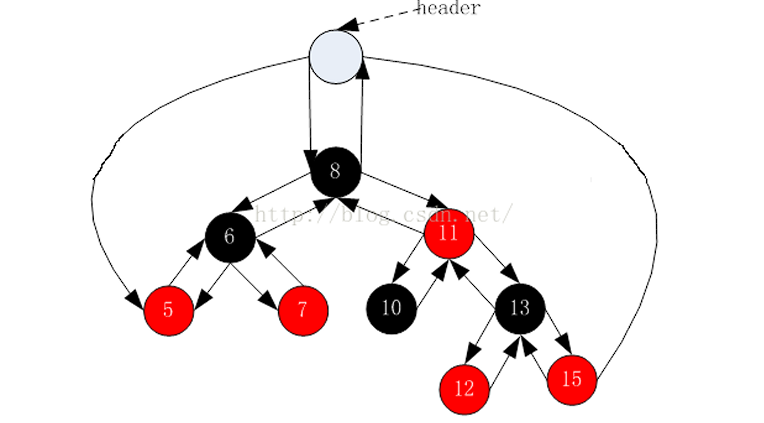
红黑树的插入
红黑树插入时也是按照二叉搜索树的规则进行插入,并在此基础上加上平衡条件,因此插入也就分为两步
- 按照二叉搜索树的规则插入新节点
- 插入节点后检测规则是否被破坏
因为插入红节点时只有可能破坏第三条规则,因此我们只需要判断父节点是否为红色即可
然后我们分情况讨论
为了方便叙述,我们约定cur为插入节点,p为父节点,g为祖父节点,u为叔叔节点
cur为红,p为红,g为黑,u存在且为红
画出来是这样的
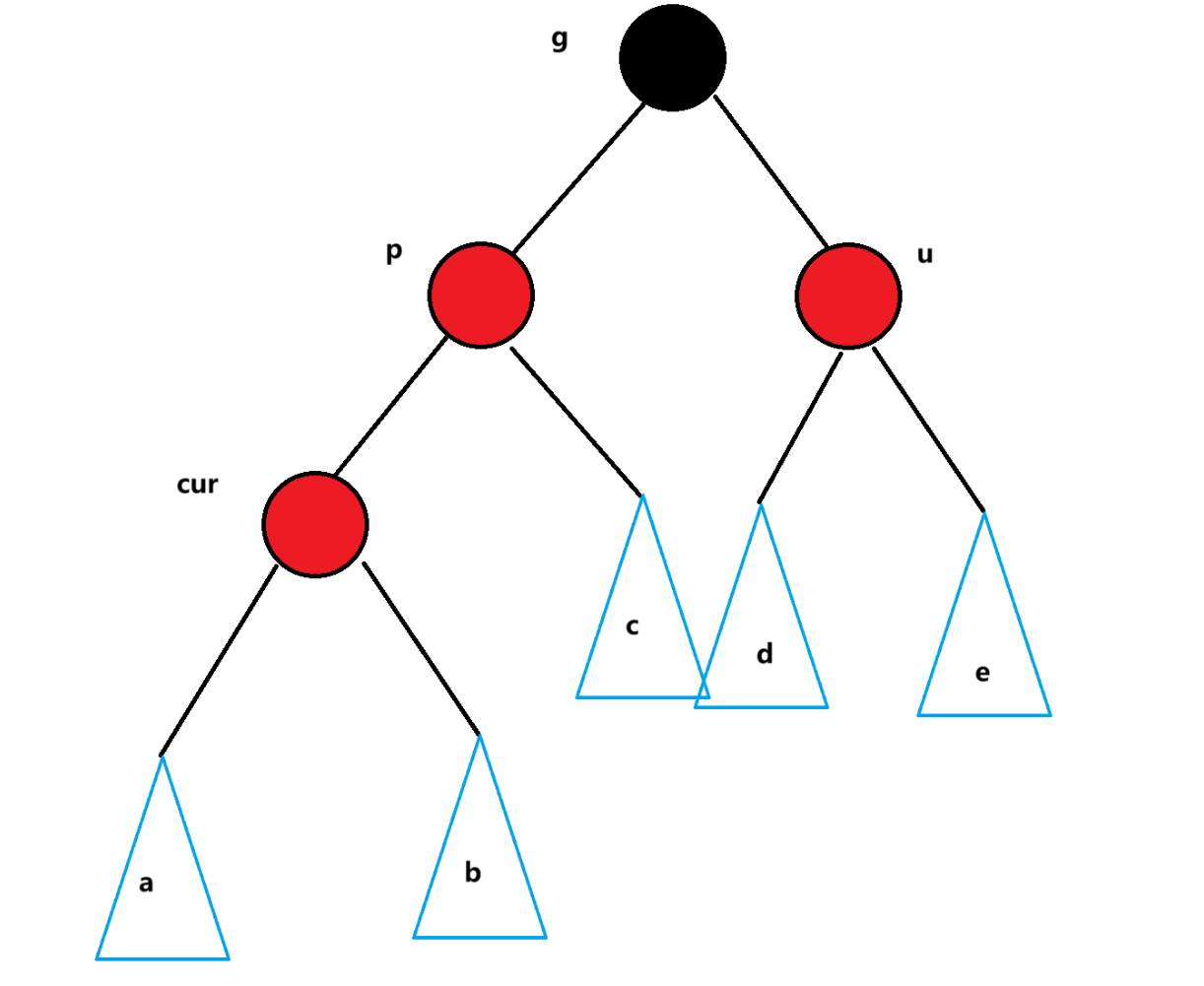
这时我们需要将g改为红色,p和u改为黑色即可,这样既能保证红色不连续,黑色数量一致,如图
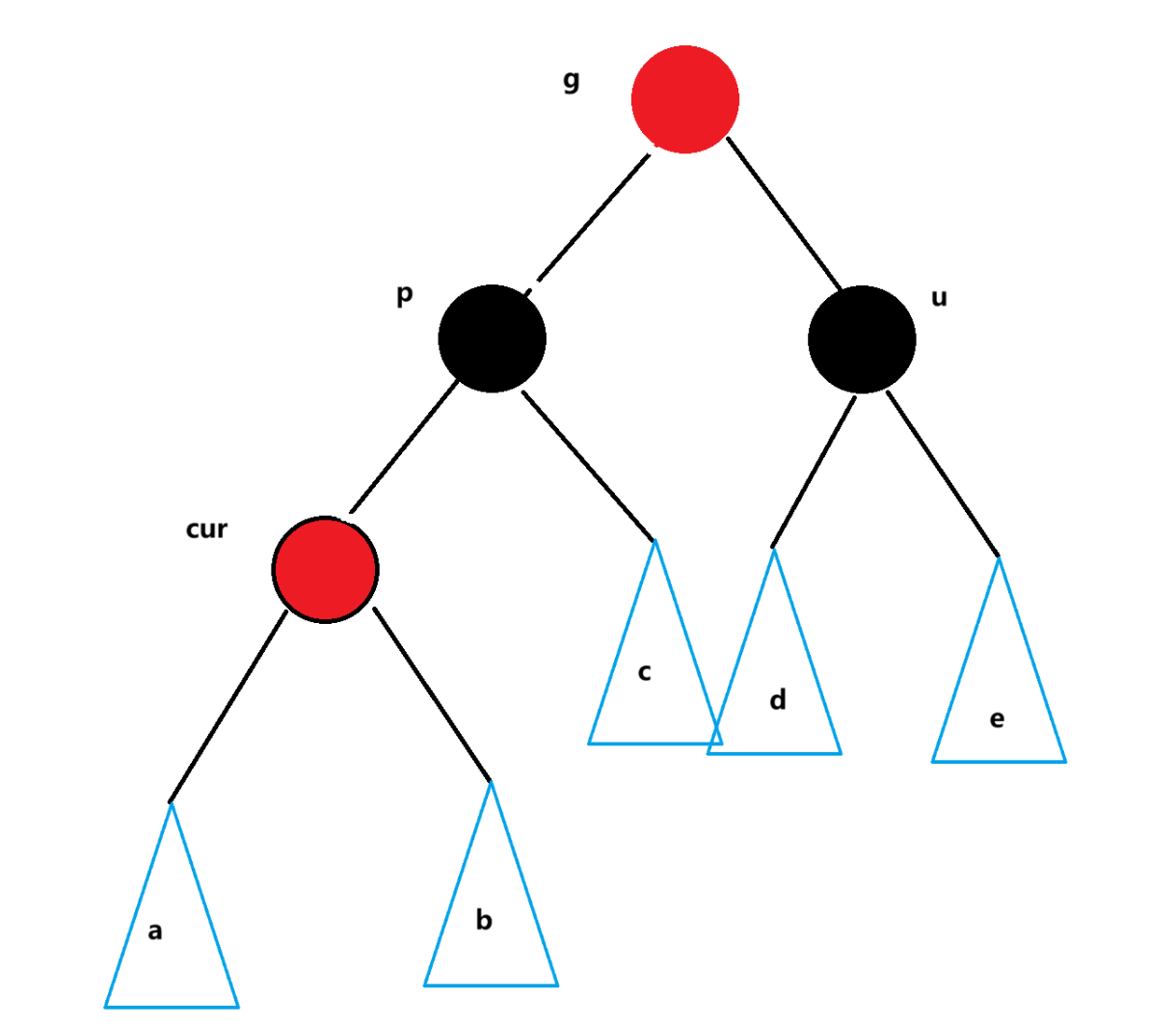
但是如果g是是子树,那么g一定有父节点,当g的父节点也是红色时,也就同样需要向上调整了
cur为红,p为红,g为黑,u不存在或u为黑,插入到p对应的一边
画出来是这样的
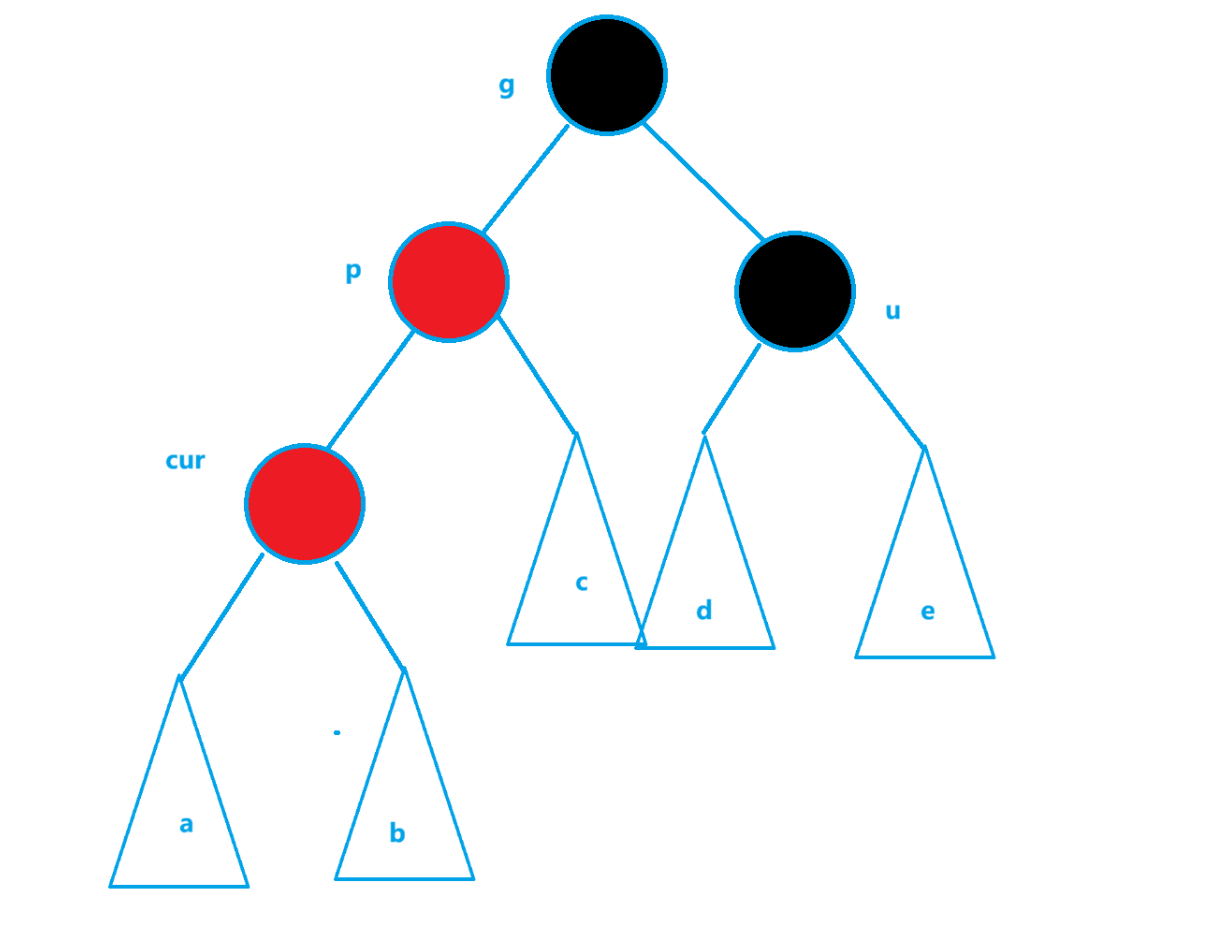
u的情况有两种
- u节点不存在,说明cur一定是新插入的节点,因为要保证左右两个路径的黑色节点的数量相同
- u节点存在,说明cur节点是由下至上调整的红色,原因也是左右路径的黑色节点要相同
对于这两种情况的调整方法是相同的,如果p是g的左节点,cur为p的左节点,则右单旋,如果p是g的右节点,cur为p的右节点,则左单旋
同时p要变成黑色,g要变成红色
变成如下状态
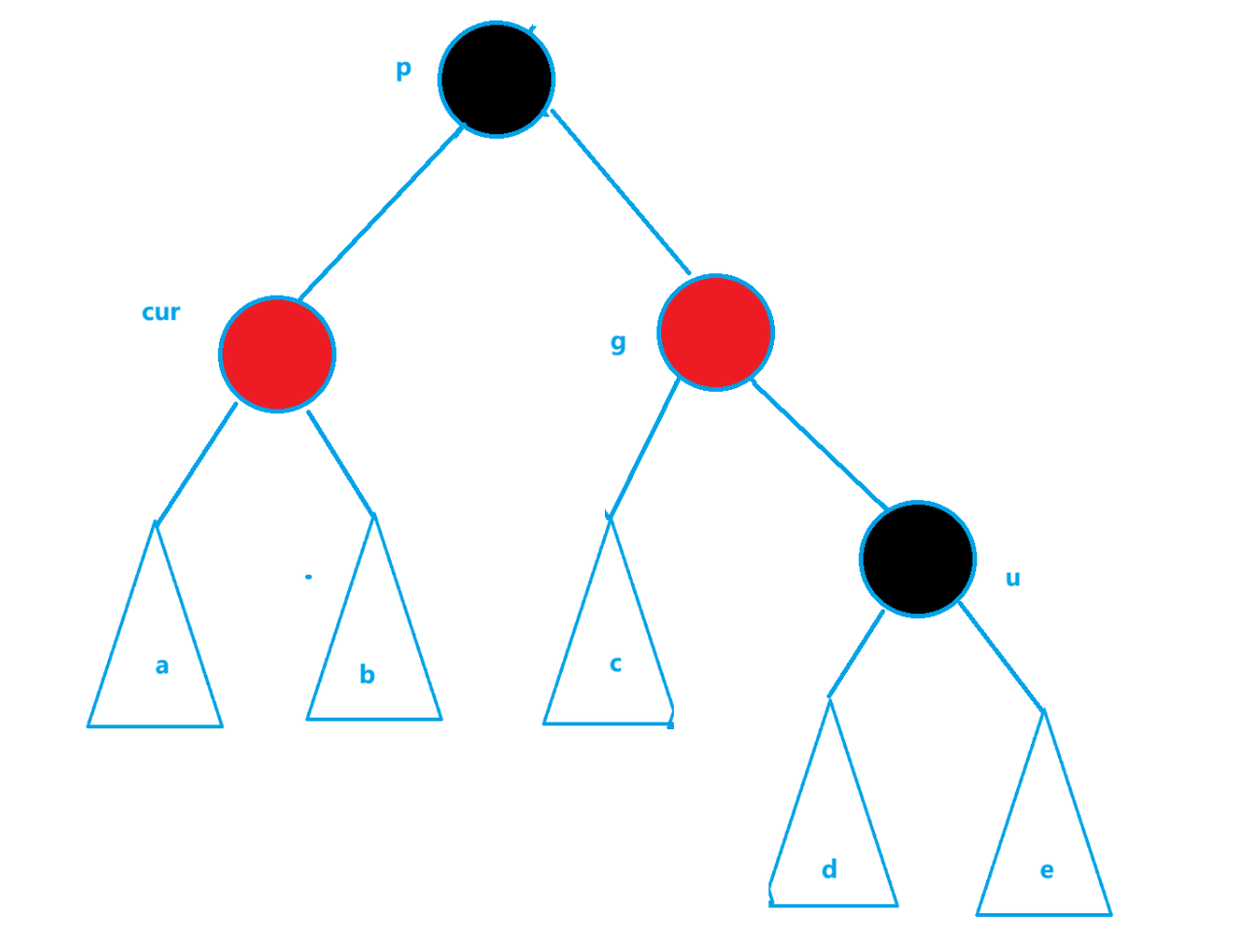
那么因为最上面的根节点颜色没有变化,也就不需要继续向上调整了
cur为红,p为红,g为黑,u不存在或u存在且为黑,插入到与p相反的一边
如图
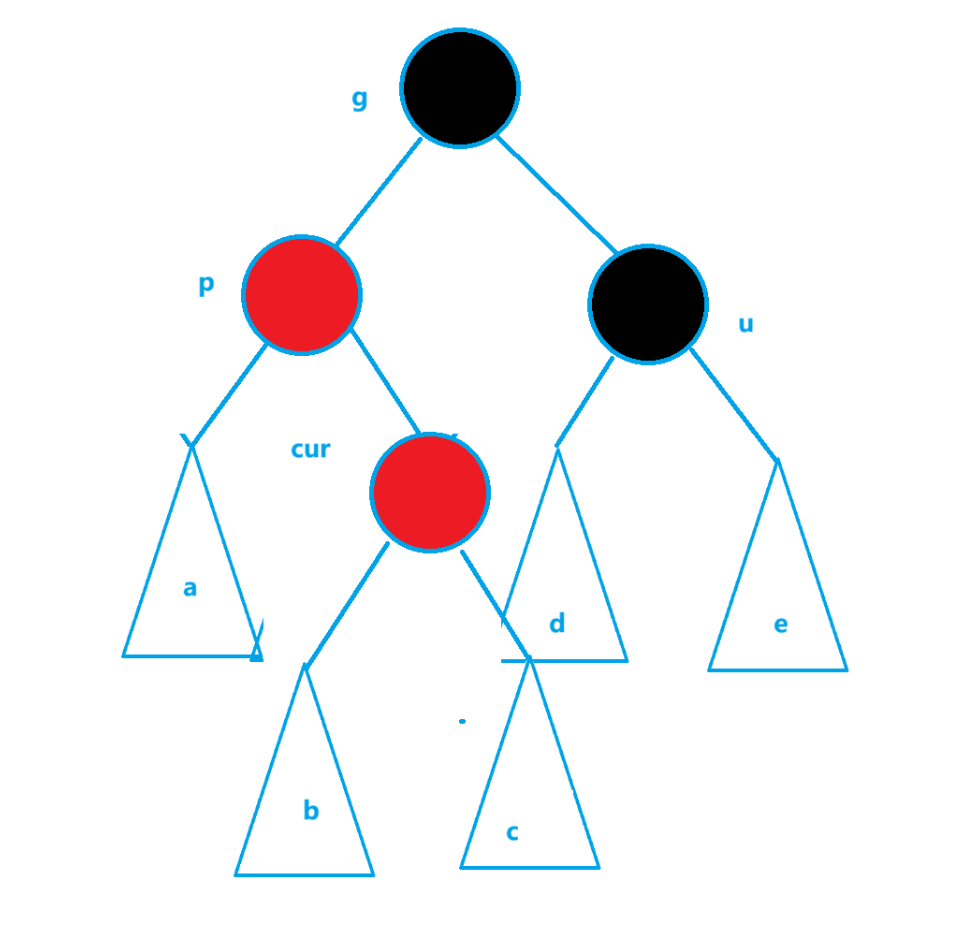
这种情况需要针对p进行单旋,如果p为g的左节点,cur为p的右节点,则对p左单旋,反之则为右单旋,此时就会变成第二种情况,再继续处理即可
第一次处理的结果如下
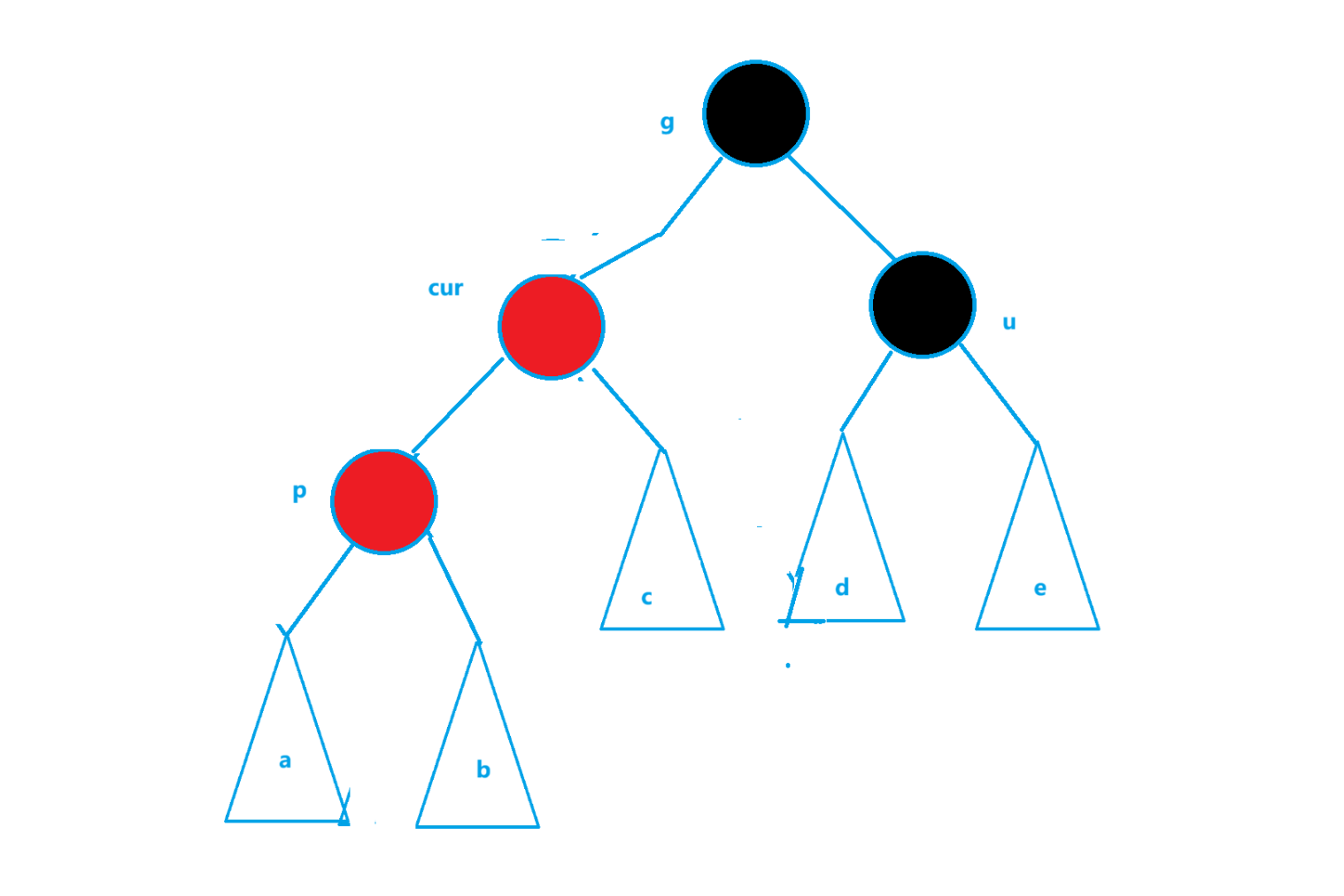
示例代码
template<class K, class T, class KeyOfT>
class RBTree {typedef RBTreeNode<T> Node;
public:pair<Node*, bool> Insert(const T& data) {// 插入根节点直接返回if (_root == nullptr) {_root = new Node(data);_root->_col = BLACK;return make_pair(_root, true);}Node* parent = nullptr;Node* cur = _root;KeyOfT kot;// 平衡二叉树找到插入位置while (cur) {if (kot(cur->_data) < kot(data)) {parent = cur;cur = cur->_right;} else if (kot(cur->_data) > kot(data)) {parent = cur;cur = cur->_left;} else {return make_pair(cur, false);}}// 新建节点cur = new Node(data);Node* newnode = cur;cur->_col = RED;// 连接父节点if (kot(parent->_data) < kot(data)) {parent->_right = cur;cur->_parent = parent;} else {parent->_left = cur;cur->_parent = parent;}// 如果父节点存在且父节点为红色则需要调整while (parent && parent->_col == RED) {Node* grandfather = parent->_parent;if (parent == grandfather->_left) {// g// p u// c // 判断u是否存在和他的颜色Node* uncle = grandfather->_right;// 如果存在且为红色if (uncle && uncle->_col == RED) {// 变色parent->_col = BLACK;uncle->_col = BLACK;grandfather->_col = RED;// 向上调整cur = grandfather;parent = cur->_parent;} else {// 如果不存在或u为黑色,需要判断同侧还是异侧// 如果是同侧if (cur == parent->_left) {// g// p// cRotateR(grandfather); // 右旋// 调整颜色parent->_col = BLACK;grandfather->_col = RED;} else {// g// p// cRotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}} else { // p = g->rNode* uncle = grandfather->_left;// g// u p// c// 判断u是否存在和他的颜色// 如果存在且为红色if (uncle && uncle->_col == RED) {// 变色parent->_col = BLACK;uncle->_col = BLACK;grandfather->_col = RED;// 向上调整cur = grandfather;parent = cur->_parent;} else {if (cur == parent->_right) {RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;} else {// g// u p // c//RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;return make_pair(newnode, true);}void RotateL(Node* parent) {Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;subR->_left = parent;Node* parentParent = parent->_parent;parent->_parent = subR;if (subRL)subRL->_parent = parent;else {if (parentParent->_left == parent) {parentParent->_left = subR;} else {parentParent->_right = subR;}subR->_parent = parentParent;}}void RotateR(Node* parent) {Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;Node* parentParent = parent->_parent;subL->_right = parent;parent->_parent = subL;if (_root == parent) {_root = subL;subL->_parent = nullptr;} else {if (parentParent->_left == parent) {parentParent->_left = subL;} else {parentParent->_right = subL;}subL->_parent = parentParent;}}
private:Node* _root = nullptr;
};
红黑树的验证
红黑树要验证需要验证两个部分
- 检测是否中序遍历是有序序列
- 检测是否满足红黑树的性质
这里我们就不讲红黑树的删除了,完成红黑树的验证之后就算作已经完成了任务,接下来会使用红黑树模拟实现map和set
红黑树与AVL树的比较
红黑树和AVL树都是高效的平衡二叉树,但是红黑树不追求绝对的平衡,降低了插入和旋转的次数,因此性能比AVL更优,而且红黑树比AVL树的实现更加简单,所以实际中运用红黑树更多
完整代码
#pragma once
#include<utility>
#include<iostream>
using namespace std;
// 颜色
enum Color {RED,BLACK
};template<class T>
struct RBTreeNode {RBTreeNode<T>* _left;RBTreeNode<T>* _right;RBTreeNode<T>* _parent;T _data;Color _col;RBTreeNode(const T& data):_left(nullptr), _right(nullptr), _parent(nullptr), _data(data), _col(RED) {}
};template<class K, class T, class KeyOfT>
class RBTree {typedef RBTreeNode<T> Node;
public:pair<Node*, bool> Insert(const T& data) {if (_root == nullptr) {_root = new Node(data);_root->_col = BLACK;return make_pair(_root, true);}Node* parent = nullptr;Node* cur = _root;KeyOfT kot;// 平衡二叉树找到插入位置while (cur) {if (kot(cur->_data) < kot(data)) {parent = cur;cur = cur->_right;} else if (kot(cur->_data) > kot(data)) {parent = cur;cur = cur->_left;} else {return make_pair(cur, false);}}// 新建节点cur = new Node(data);Node* newnode = cur;cur->_col = RED;// 连接父节点if (kot(parent->_data) < kot(data)) {parent->_right = cur;cur->_parent = parent;} else {parent->_left = cur;cur->_parent = parent;}// 如果父节点存在且父节点为红色则需要调整while (parent && parent->_col == RED) {Node* grandfather = parent->_parent;if (parent == grandfather->_left) {// g// p u// c // 判断u是否存在和他的颜色Node* uncle = grandfather->_right;// 如果存在且为红色if (uncle && uncle->_col == RED) {// 变色parent->_col = BLACK;uncle->_col = BLACK;grandfather->_col = RED;// 向上调整cur = grandfather;parent = cur->_parent;} else {// 如果不存在或u为黑色,需要判断同侧还是异侧// 如果是同侧if (cur == parent->_left) {// g// p// cRotateR(grandfather); // 右旋// 调整颜色parent->_col = BLACK;grandfather->_col = RED;} else {// g// p// cRotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}} else { // p = g->rNode* uncle = grandfather->_left;// g// u p// c// 判断u是否存在和他的颜色// 如果存在且为红色if (uncle && uncle->_col == RED) {// 变色parent->_col = BLACK;uncle->_col = BLACK;grandfather->_col = RED;// 向上调整cur = grandfather;parent = cur->_parent;} else {if (cur == parent->_right) {RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;} else {// g// u p // c//RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;return make_pair(newnode, true);}void RotateL(Node* parent) {Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;subR->_left = parent;Node* parentParent = parent->_parent;parent->_parent = subR;if (subRL)subRL->_parent = parent;else {if (parentParent->_left == parent) {parentParent->_left = subR;} else {parentParent->_right = subR;}subR->_parent = parentParent;}}void RotateR(Node* parent) {Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;Node* parentParent = parent->_parent;subL->_right = parent;parent->_parent = subL;if (_root == parent) {_root = subL;subL->_parent = nullptr;} else {if (parentParent->_left == parent) {parentParent->_left = subL;} else {parentParent->_right = subL;}subL->_parent = parentParent;}}void InOrder() {_InOrder(_root);cout << endl;}void _InOrder(Node* root) {if (root == nullptr)return;_InOrder(root->_left);cout << root->_data << ' ';_InOrder(root->_right);}bool Check(Node* root, int blacknum, const int refVal) {if (root == nullptr) {if (blacknum != refVal) {cout << "存在黑色节点数量不相等的路径" << endl;return false;}return true;}if (root->_col == RED && root->_parent->_col == RED) {cout << "存在连续的红节点" << endl;return false;}if (root->_col == BLACK) {++blacknum;}return Check(root->_left, blacknum, refVal) && Check(root->_right, blacknum, refVal);}bool IsBalance() {if (_root == nullptr)return true;if (_root->_col == RED)return false;int refVal = 0; // 参考值Node* cur = _root;while (cur) {if (cur->_col == BLACK) {++refVal;}cur = cur->_left;}int blacknum = 0;return Check(_root, blacknum, refVal);}int Height() {return _Height(_root);}int _Height(Node* root) {if (root == nullptr)return 0;int leftH = _Height(root->_left);int rightH = _Height(root->_right);return leftH + rightH;}size_t Size() {return _Size(_root);}size_t _Size(Node* root) {if (root == nullptr)return 0;return _Size(root->_left) + _Size(root->_right) + 1;}Node* Find(const K& key) {Node* cur = _root;while (cur) {if (cur->_data < key) {cur = cur->_right;}else if (cur->_data > key) {cur = cur->_left;}else {return cur;}}return nullptr;}private:Node* _root = nullptr;
};
相关文章:

C++手撕红黑树
文章目录 红黑树概念性质(条件限制)节点的定义红黑树的结构红黑树的插入cur为红,p为红,g为黑,u存在且为红cur为红,p为红,g为黑,u不存在或u为黑,插入到p对应的一边cur为红…...

计算机中,逻辑端口
计算机中,端口是什么 在计算机领域中,端口(Port)是一个逻辑概念,用于标识计算机与外部设备或另一台计算机通信时的出入口。它是计算机与外部通信的途径,分为物理端口和逻辑端口两种。 物理端口:物理端口也被称为接口,是计算机主板上或其他设备上的硬件接口,如USB接口…...

SV学习笔记(一)
SV:SystemVerilog 开启SV之路 数据类型 內建数据类型 四状态与双状态 : 四状态指0、1、X、Z,包括logic、integer、 reg、 wire。双状态指0、1,包括bit、byte、 shortint、int、longint。 有符号与无符号 : 有符号&am…...
大型商业银行基础设施的用户安全管理创新与实践
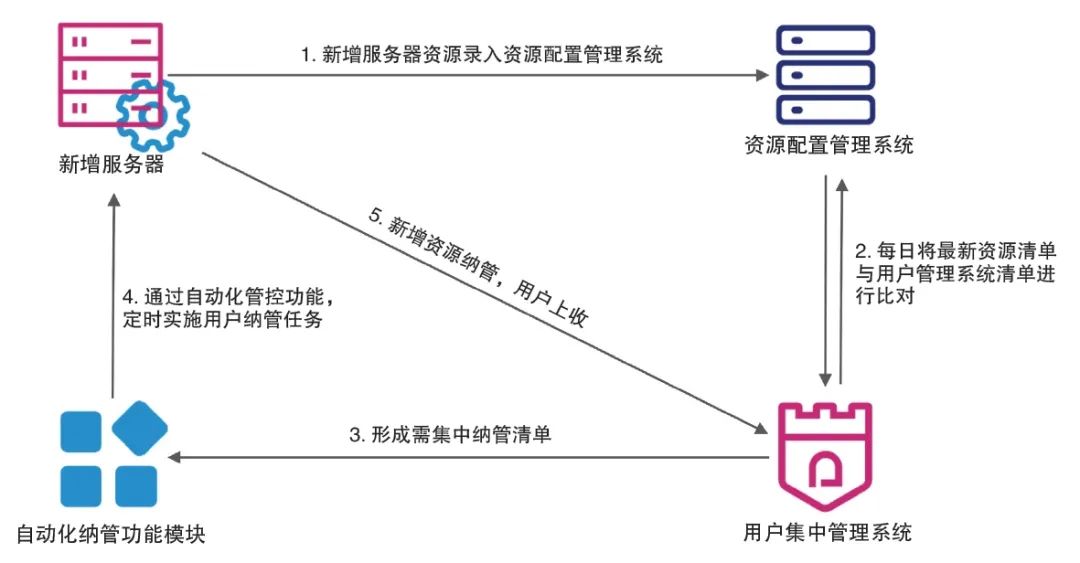
文丨中国工商银行数据中心安全运营部 陈茜倩 王喆 基础设施的用户安全一直是银行业信息系统稳定运行的重要保障,近年来,随着科技的快速发展,针对用户安全的攻击方式层出不穷,如网络钓鱼、恶意软件、身份盗用、弱密码攻击、社交工程…...

数据库入门-----SQL基础知识
目录 📖前言: 📑SQL概述&&通用语法: 🐳DDL: 🐻操作数据库: 🐞数据类型: 🦉操作表: 🦦DML: 语法规则&#x…...
本地代码第一次提交到远程仓库gitee
1.在gitee新建仓库 2.新建一个空文件夹 打开黑窗口,执行命令 克隆仓库地址 执行命令 git clone https://gitee.com/llncomms/test.git打开隐藏的项目 复制全部内容到需要提交的代码中 3.在提交的代码中执行命令 $ git add .git commit -m 首次提交$ git push提交成功...
)
蓝桥杯刷题 深度优先搜索-[178]全球变暖(C++)
题目描述 你有一张某海域 NN 像素的照片,”.”表示海洋、”#”表示陆地,如下所示: … .##… .##… …##. …####. …###. … 其中”上下左右”四个方向上连在一起的一片陆地组成一座岛屿,例如上图就有 2 座岛屿。 由于全球变暖…...

C语言-函数指针-快速排序算法(书籍示例-入门)
概述 使用C语言,实现结构体多元素,排序算法(冒泡排序),这里使用示例:书籍示例讲解 函数简介 函数声明 void qsort(void *base, size_t nitems, size_t size, int (*compar)(const void *, const void*)) 参…...

# 计算机视觉入门
## 概述 计算机视觉(Computer Vision)是人工智能的重要分支领域,它关注于如何使计算机“看”懂图像或视频内容,并从中提取有用信息,对视觉数据进行处理和理解。随着深度学习技术的兴起,计算机视觉领域取得…...

React - 你知道useffect函数内如何模拟生命周期吗
难度级别:中级及以上 提问概率:65% 很多前端开发人员习惯了Vue或者React的组件式开发,熟知组件的周期过程包含初始化、挂载完成、修改和卸载等阶段。但是当使用Hooks做业务开发的时候,看见一个个useEffect函数,却显得有些迷茫,因为在us…...

电子元器件批发商的市场营销策略与推广技巧
引言 电子元器件批发商面临激烈的市场竞争,有效的市场营销策略和推广技巧对于提升品牌知名度、吸引客户和促进销售至关重要。本文将探讨电子元器件批发商的市场营销策略与推广技巧,助力企业在竞争激烈的市场中取得成功。 1. 精准定位目标客户 行业细分…...

大型语言模型(LLMs)面试常见问题解析
概述 这篇文章[1]是关于大型语言模型(LLMs)的面试问题和答案,旨在帮助读者准备相关职位的面试。 token? 在大型语言模型中,token 指的是什么? 分词(Tokenization):可以将…...
 |请求方法及状态码)
【接口】HTTP(2) |请求方法及状态码
1、HTTP常用请求方法 get:获取资源或指定的数据 请求指定的页面信息,返回实体主体(查询) post:发送数据给服务器,创建或更新资源 put:创建/替换目标资源 delete:删除资源 get …...
CSS设置网页颜色
目录 前言: 1.颜色名字: 2.十六进制码: 3.RGB: 4.RGBA: 5.HSL: 1.hue: 2.saturation: 3.lightness: 6.HSLA: 前言: 我们在电脑显示器&…...

R语言数据操纵:常用函数
目录 处理循环的函数 lapply函数 apply函数 mapply函数 tapply函数 split函数 排序的函数 sort函数与order函数 总结数据信息的函数 head函数与tail函数 summary函数 str函数 table函数 any函数 all函数 xtab函数 object.size函数 这篇文章主要介绍R语言中处理…...

图论做题笔记:bfs
Leetcode - 433:最小基因变化 题目: 基因序列可以表示为一条由 8 个字符组成的字符串,其中每个字符都是 A、C、G 和 T 之一。 假设我们需要调查从基因序列 start 变为 end 所发生的基因变化。一次基因变化就意味着这个基因序列中的一个字符发生了变化…...

群集服务器与主机托管区别
1、首先什么群集服务器? 通俗的来说,它是指很多台服务器把它们集中在一起来进行同一种服务,而在我们在客户端看,却只能看见一个服务器;集群服务器也可以由很多个的计算机并行去计算,这样可以获得非常高的计算速度;同时也可以用很多个计算机来…...

Linux锁的使用
一、临界资源与临界区 多线程会共享例如全局变量等资源,我们把会被多个执行流访问的资源称为临界资源,我们是通过代码访问临界资源的,而我们访问临界资源的那部分代码称为临界区。 实现一个抢票系统 只有一个线程抢票时 #include <ios…...

go语言学习--2.函数
目录 1.函数分类 2.函数的声明和定义 3.函数传参 4.函数返回值 5.递归调用 为完成某一功能的程序指令(语句)的集合,称为函数。 1.函数分类 在Go语言中,函数是第一类对象,我们可以将函数保持到变量中。函数主要有具名和匿名之分&#x…...

[安卓逆向]常见调试和反调试及解决方案
写在前面 我们在逆向软件时难免会遇到一些反调试策略,这篇文章就来详细总结下,现阶段比较流行的几种反调试策略及解决方案。 特定文件检测 反调试功能: 通过检测文件方式,检测android_server文件是否存在设备中的指定目录/data/l…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...
【记录坑点问题】IDEA运行:maven-resources-production:XX: OOM: Java heap space
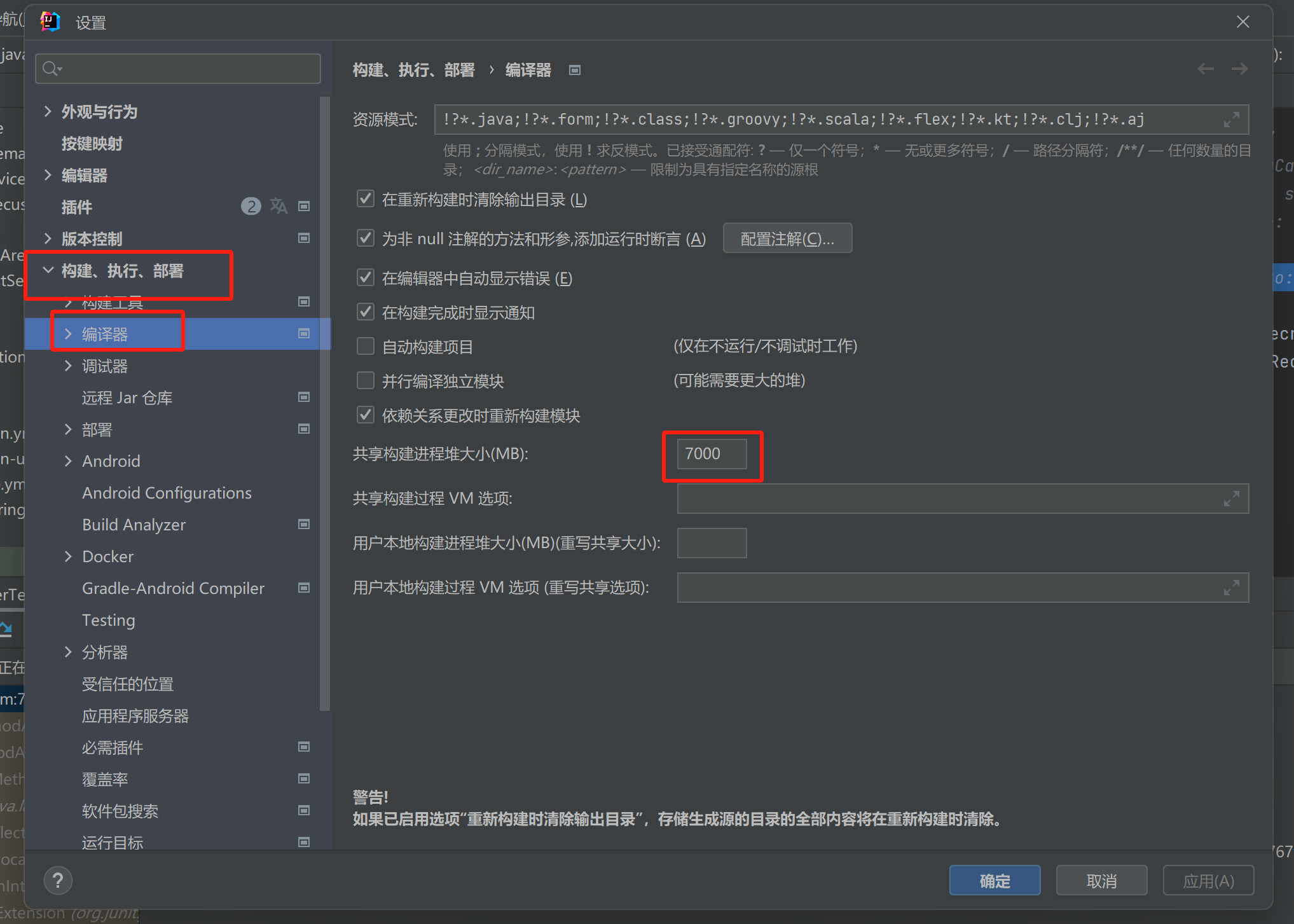
问题:IDEA出现maven-resources-production:operation-service: java.lang.OutOfMemoryError: Java heap space 解决方案:将编译的堆内存增加一点 位置:设置setting-》构建菜单build-》编译器Complier...

Spring事务传播机制有哪些?
导语: Spring事务传播机制是后端面试中的必考知识点,特别容易出现在“项目细节挖掘”阶段。面试官通过它来判断你是否真正理解事务控制的本质与异常传播机制。本文将从实战与源码角度出发,全面剖析Spring事务传播机制,帮助你答得有…...
)
Spring Boot 与 Kafka 的深度集成实践(二)
3. 生产者实现 3.1 生产者配置 在 Spring Boot 项目中,配置 Kafka 生产者主要是配置生产者工厂(ProducerFactory)和 KafkaTemplate 。生产者工厂负责创建 Kafka 生产者实例,而 KafkaTemplate 则是用于发送消息的核心组件&#x…...
