【进阶六】Python实现SDVRPTW常见求解算法——遗传算法(GA)
基于python语言,采用经典蚁群算法(ACO)对 带硬时间窗的需求拆分车辆路径规划问题(SDVRPTW) 进行求解。
目录
- 往期优质资源
- 1. 适用场景
- 2. 代码调整
- 2.1 需求拆分
- 2.2 需求拆分后的服务时长取值问题
- 3. 求解结果
- 4. 代码片段
往期优质资源
经过一年多的创作,目前已经成熟的代码列举如下,如有需求可私信联系,表明需要的 **问题与算法**,原创不宜,有偿获取。
| VRP问题 | GA | ACO | ALNS | DE | DPSO | QDPSO | TS | SA |
|---|---|---|---|---|---|---|---|---|
| CVRP | √ | √ | √ | √ | √ | √ | √ | √ |
| VRPTW | √ | √ | √ | √ | √ | √ | √ | √ |
| MDVRP | √ | √ | √ | √ | √ | √ | √ | √ |
| MDHVRP | √ | √ | √ | √ | √ | √ | √ | √ |
| MDHVRPTW | √ | √ | √ | √ | √ | √ | √ | √ |
| SDVRP | √ | √ | √ | √ | √ | √ | √ | √ |
| SDVRPTW | √ | √ |
1. 适用场景
- 求解SDVRPTW
- 车辆类型单一
- 车辆容量小于部分需求节点需求
- 单一车辆基地
- 带硬时间窗
2. 代码调整
2.1 需求拆分
与SDVRP问题相比,SDVRPTW问题不仅允许客户需求大于车辆载重,而且考虑了客户节点的时间窗约束。为了使得每个客户的需求得到满足,必须派遣一辆或多辆车辆在规定时间窗内对客户进行服务。对于需求节点的拆分,这里依然采取先验拆分策略,本文采用文献[1]提出的先验分割策略,表述如下:
(1)20/10/5/1拆分规则
- m20 =max{ m ∈ Z + ∪ { 0 } ∣ 0.20 Q m < = D i m\in Z^+ \cup \{0\} | 0.20Qm <= D_i m∈Z+∪{0}∣0.20Qm<=Di }
- m10 =max{ m ∈ Z + ∪ { 0 } ∣ 0.10 Q m < = D i − 0.20 Q m 20 m\in Z^+ \cup \{0\} | 0.10Qm <= D_i-0.20Qm_{20}~ m∈Z+∪{0}∣0.10Qm<=Di−0.20Qm20 }
- m5 =max{ m ∈ Z + ∪ { 0 } ∣ 0.05 Q m < = D i − 0.20 Q m 20 − 0.10 Q m 10 m\in Z^+ \cup \{0\} | 0.05Qm <= D_i-0.20Qm_{20}-0.10Qm_{10} m∈Z+∪{0}∣0.05Qm<=Di−0.20Qm20−0.10Qm10 }
- m1 =max{ m ∈ Z + ∪ { 0 } ∣ 0.01 Q m < = D i − 0.20 Q m 20 − 0.10 Q m 10 − 0.05 Q m 5 m\in Z^+ \cup \{0\} | 0.01Qm <= D_i-0.20Qm_{20}-0.10Qm_{10}-0.05Qm_{5} m∈Z+∪{0}∣0.01Qm<=Di−0.20Qm20−0.10Qm10−0.05Qm5 }
(2)25/10/5/1拆分规则
- m25 =max{ m ∈ Z + ∪ { 0 } ∣ 0.25 Q m < = D i m\in Z^+ \cup \{0\} | 0.25Qm <= D_i m∈Z+∪{0}∣0.25Qm<=Di }
- m10 =max{ m ∈ Z + ∪ { 0 } ∣ 0.10 Q m < = D i − 0.25 Q m 25 m\in Z^+ \cup \{0\} | 0.10Qm <= D_i-0.25Qm_{25}~ m∈Z+∪{0}∣0.10Qm<=Di−0.25Qm25 }
- m5 =max{ m ∈ Z + ∪ { 0 } ∣ 0.05 Q m < = D i − 0.25 Q m 25 − 0.10 Q m 10 m\in Z^+ \cup \{0\} | 0.05Qm <= D_i-0.25Qm_{25}-0.10Qm_{10} m∈Z+∪{0}∣0.05Qm<=Di−0.25Qm25−0.10Qm10 }
- m1 =max{ m ∈ Z + ∪ { 0 } ∣ 0.01 Q m < = D i − 0.25 Q m 25 − 0.10 Q m 10 − 0.05 Q m 5 m\in Z^+ \cup \{0\} | 0.01Qm <= D_i-0.25Qm_{25}-0.10Qm_{10}-0.05Qm_{5} m∈Z+∪{0}∣0.01Qm<=Di−0.25Qm25−0.10Qm10−0.05Qm5 }
在实现过程中,对于需求超过车辆容量的客户必须进行需求拆分,而对于未超过车辆容量的客户可以拆分也可以不拆分,这里设置了参数比例进行限制。
2.2 需求拆分后的服务时长取值问题
节点的服务时长会影响车辆的行进时间,进而会影响与节点时间窗的匹配问题。一般来说,节点的服务时长与需求量成正比关系,在进行节点需求拆分后,新节点的需求量降低,其服务时长理应也降低。但从标准数据集来看,各需求节点的服务时长均采用同一数值。因此本文在代码实现过程中也采用固定值,不考虑新节点服务时长的变化。当然,如有需要,也可以设置单位货物的服务时长,根据拆分后节点的具体需求量设置相应的服务时长。
3. 求解结果
(1)收敛曲线

(2)车辆路径

(3)输出内容

4. 代码片段
(1)数据结构
# 数据结构:解
class Sol():def __init__(self):self.obj=None # 目标函数值self.node_no_seq=[] # 解的编码self.route_list=[] # 解的解码self.timetable_list=[] # 车辆访问各点的时间self.route_distance_list = None
# 数据结构:需求节点
class Node():def __init__(self):self.id=0 # 节点idself.x_coord=0 # 节点平面横坐标self.y_coord=0 # 节点平面纵坐标self.demand=0 # 节点需求self.start_time=0 # 节点开始服务时间self.end_time=1440 # 节点结束服务时间self.service_time=0 # 单次服务时长self.vehicle_speed = 0 # 行驶速度
# 数据结构:车场节点
class Depot():def __init__(self):self.id=0 # 节点idself.x_coord=0 # 节点平面横坐标self.y_coord=0 # 节点平面纵坐标self.start_time=0 # 节点开始服务时间self.end_time=1440 # 节点结束服务时间self.v_speed = 0 # 行驶速度self.v_cap = 80 # 车辆容量
# 数据结构:全局参数
class Model():def __init__(self):self.best_sol=None # 全局最优解self.sol_list=[] # 解的集合self.demand_dict = {} # 需求节点集合self.depot = None # 车场节点集合self.demand_id_list = [] # 需求节点id集合self.distance_matrix = {} # 距离矩阵self.time_matrix = {} # 时间矩阵self.number_of_demands = 0 # 需求点数量self.demand_id_list_ = [] # 经先验需求分割后的节点集合self.demand_dict_ = {} # 需求分割后的节点需求集合self.distance_matrix_ = {} # 原始节点id间的距离矩阵self.time_matrix_ = {} # 原始节点id间的时间矩阵self.mapping = {} # 需求分割前后的节点对应关系self.split_rate = 0.5 # 控制需求分割的比例(需求超出车辆容量的除外)self.popsize = 100 # 种群规模self.alpha = 2 # 信息启发式因子self.beta = 3 # 期望启发式因子self.Q = 100 # 信息素总量self.rho = 0.5 # 信息素挥发因子self.tau = {} # 弧信息素集合self.tau0 = 100 # 路径初始信息素
(2)距离矩阵
# 初始化参数:计算距离矩阵时间矩阵
def calDistanceTimeMatrix(model):for i in range(len(model.demand_id_list)):from_node_id = model.demand_id_list[i]for j in range(len(model.demand_id_list)):to_node_id = model.demand_id_list[j]dist = math.sqrt((model.demand_dict[from_node_id].x_coord - model.demand_dict[to_node_id].x_coord) ** 2+ (model.demand_dict[from_node_id].y_coord - model.demand_dict[to_node_id].y_coord) ** 2)model.distance_matrix[from_node_id, to_node_id] = distmodel.time_matrix[from_node_id,to_node_id] = math.ceil(dist/model.depot.v_speed)dist = math.sqrt((model.demand_dict[from_node_id].x_coord - model.depot.x_coord) ** 2 +(model.demand_dict[from_node_id].y_coord - model.depot.y_coord) ** 2)model.distance_matrix[from_node_id, model.depot.id] = distmodel.distance_matrix[model.depot.id, from_node_id] = distmodel.time_matrix[from_node_id,model.depot.id] = math.ceil(dist/model.depot.v_speed)model.time_matrix[model.depot.id,from_node_id] = math.ceil(dist/model.depot.v_speed)
(3)邻域搜索
# 蚂蚁移动
def movePosition(model):sol_list=[]local_sol=Sol()local_sol.obj=float('inf')for _ in range(model.popsize):#随机初始化蚂蚁为止node_no_seq=[random.randint(0,len(model.demand_id_list_)-1)]all_node_no_seq=copy.deepcopy(model.demand_id_list_)all_node_no_seq.remove(node_no_seq[-1])#确定下一个访问节点while len(all_node_no_seq)>0:next_node_no=searchNextNode(model,node_no_seq[-1],all_node_no_seq)node_no_seq.append(next_node_no)all_node_no_seq.remove(next_node_no)sol=Sol()sol.node_no_seq=node_no_seqsol.timetable_list,sol.obj, sol.route_distance,sol.route_list = calObj(node_no_seq,model)sol_list.append(sol)if sol.obj < local_sol.obj:local_sol = copy.deepcopy(sol)model.sol_list=copy.deepcopy(sol_list)if local_sol.obj<model.best_sol.obj:model.best_sol=copy.deepcopy(local_sol)
# 搜索下一移动节点
def searchNextNode(model,current_node_no,SE_List):prob=np.zeros(len(SE_List))for i,node_no in enumerate(SE_List):eta=1/model.distance_matrix_[current_node_no,node_no] if model.distance_matrix_[current_node_no,node_no] else 0.0001tau=model.tau[current_node_no,node_no]prob[i]=((eta**model.alpha)*(tau**model.beta))#采用轮盘法选择下一个访问节点cumsumprob=(prob/sum(prob)).cumsum()cumsumprob -= np.random.rand()return SE_List[list(cumsumprob >= 0).index(True)]
# 参考
【1】 A novel approach to solve the split delivery vehicle routing problem
相关文章:

【进阶六】Python实现SDVRPTW常见求解算法——遗传算法(GA)
基于python语言,采用经典蚁群算法(ACO)对 带硬时间窗的需求拆分车辆路径规划问题(SDVRPTW) 进行求解。 目录 往期优质资源1. 适用场景2. 代码调整2.1 需求拆分2.2 需求拆分后的服务时长取值问题 3. 求解结果4. 代码片段…...

【Android】App通信基础架构相关类源码解析
应用通信基础架构相关类源码解析 这里主要对Android App开发时,常用到的一些通信基础类进行一下源码的简单分析,包括: Handler:处理器,与某个Looper(一个线程对应一个Looper)进行关联。用于接…...

06-kafka配置
生产者配置 NAMEDESCRIPTIONTYPEDEFAULTVALID VALUESIMPORTANCEbootstrap.servershost/port列表,用于初始化建立和Kafka集群的连接。列表格式为host1:port1,host2:port2,…,无需添加所有的集群地址,kafka会根据提供的地址发现其他的地址&…...
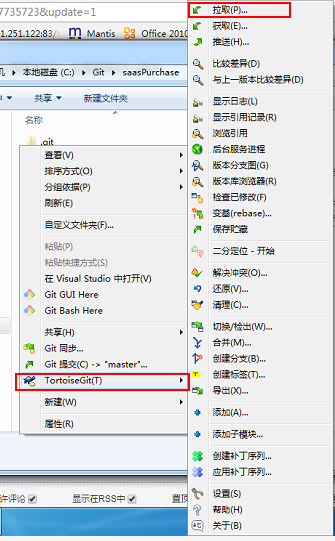
Git、TortoiseGit、SVN、TortoiseSVN 的关系和区别
Git、TortoiseGit、SVN、TortoiseSVN 的关系和区别 (一)Git(分布式版本控制系统):(二)SVN(集中式版本控制系统)(三)TortoiseGit一、下载安装 git二、安装过程…...
)
4月5日排序算法总结(1)
冒泡排序 利用每趟都确定出一个最大值或者最小值 如果需要排一个从小到大的数组,那么我们每一趟都要确定一个最大值放在最后,一共有n个数,我们最多需要排列n-1趟就可以了,我们可以改进自己的代码,利用一个flag标记&a…...

Pandas追加写入文件的时候写入到了第一行
# 原代码 def find_money(file_path, account, b_account, money, type_word, time):file pd.read_excel(file_path)with open(money.csv, a, newline, encodingutf-8) as f:for i in file.index:省略中间的代码if 省略中间的代码:file.loc[[i]].to_csv(f,indexFalse)find_sam…...
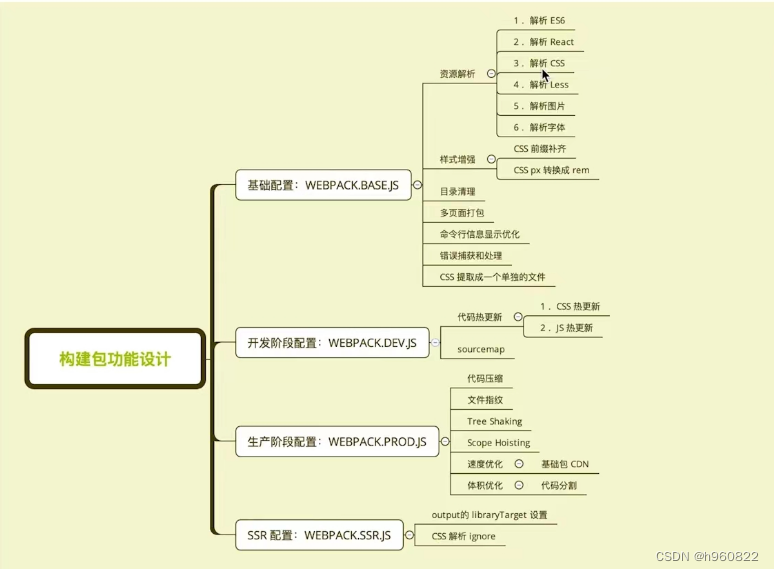
04---webpack编写可维护的构建配置
01 构建配置抽离成npm包; 意义:通用性: 业务开发者无需关注构建配置 统一团队构建脚本可维护性:构建配置合理的拆分 质量:冒烟测试 单元测试 持续集成构建配置管理的可选方案:1 通过多个配置文件管理不同…...

【云计算】云数据中心网络(一):VPC
云数据中心网络(一):VPC 1.什么是 VPC2.VPC 的组成2.1 虚拟交换机2.2 虚拟路由器 3.VPC 网络规划3.1 VPC 数量规划3.2 交换机数量规划3.3 地址空间规划3.4 不同规模企业地址空间规划实践 4.VPC 网络高可靠设计4.1 单地域单可用区部署4.2 单地…...

自动驾驶中的多目标跟踪_第一篇
自动驾驶中的多目标跟踪:第一篇 多目标跟踪(multi-object/multi-target tracking)的任务包括估计场景中目标的数目、位置(状态)或其他属性,最关键的是需要在一段时间内持续地进行估计。 附赠自动驾驶学习资料和量产经验:链接 应…...

AI爆款文案 巧用AI大模型让文案变现插上翅膀
💂 个人网站:【 摸鱼游戏】【神级代码资源网站】【工具大全】🤟 一站式轻松构建小程序、Web网站、移动应用:👉注册地址🤟 基于Web端打造的:👉轻量化工具创作平台💅 想寻找共同学习交…...
)
Python入门的60个基础练习(一)
01-Hello World python的语法逻辑完全靠缩进,建议缩进4个空格。如果是顶级代码,那么必须顶格书写,哪怕只有一个空格也会有语法错误。下面示例中,满足if条件要输出两行内容,这两行内容必须都缩进,而且具有相…...
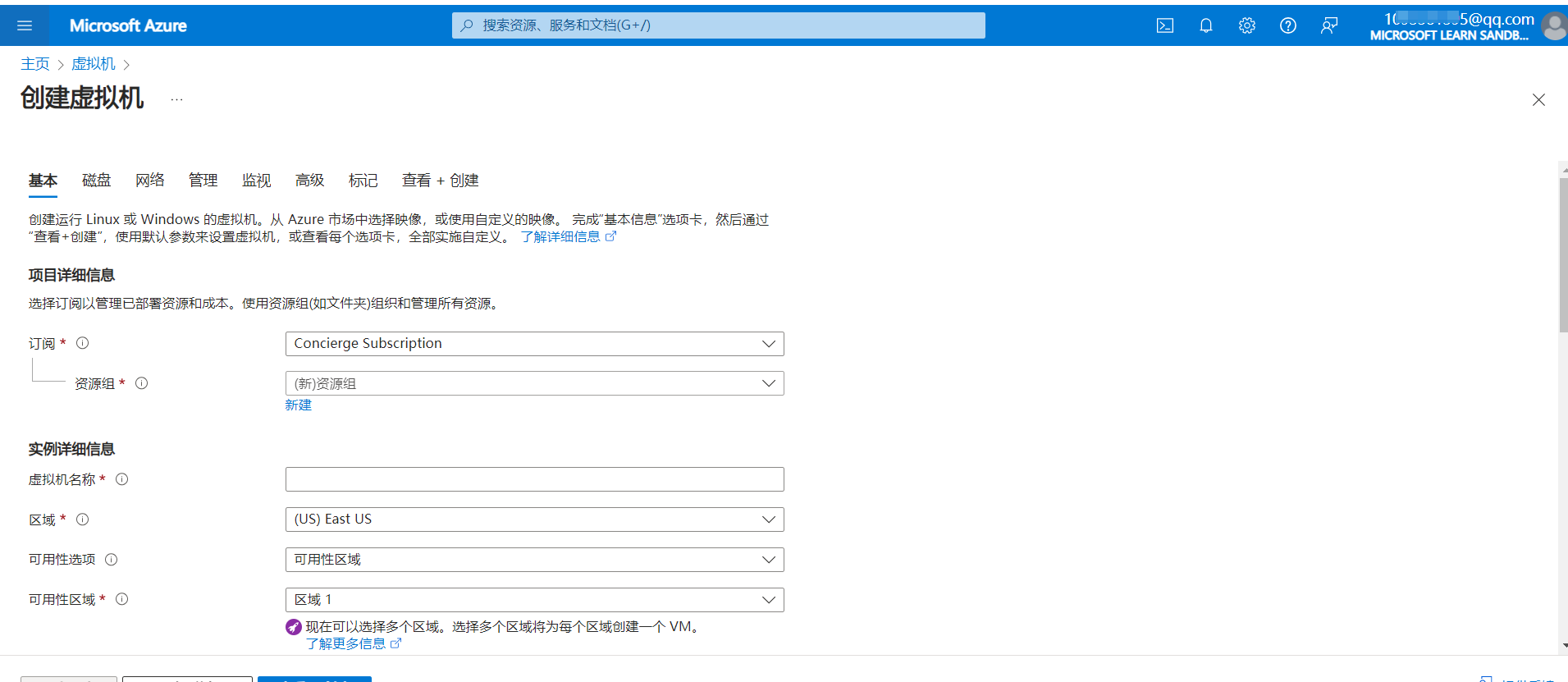
微软云学习环境
微软公有云 - Microsoft Azure 本文介绍通过微软学习中心Microsoft Learn来免费试用Azure上的服务,也不需要绑定信用卡。不过每天只有几个小时的时间。 官网 https://docs.microsoft.com/zh-cn/learn/ 实践 比如创建虚拟机,看到自己的账号下多了Learn的…...

大厂面试:找出数组中第k大的数的最佳算法
一.前置条件 假如数组为a,大小为n,要找到数组a中第k大的数。 二.解决方案 1.使用任意一种排序算法(例如快速排序)将数组a进行从大到小的排序,则第n-k个数即为答案。 2.构造一个长度为k的数组,将前k个数复制过来并降序…...

爬取高校专业信息的Python爬虫简介与实践
1. 介绍 在当前高校专业信息繁多的情况下,选择适合自己的专业成为了许多学生面临的挑战。为了帮助学生更好地了解各高校专业情况,我们开发了一个Python爬虫程序,用于爬取高校专业信息并保存到Excel文件中。本文将详细介绍该爬虫的实现过程以…...

redis 集群模式(redis cluster)介绍
目录 一 redis cluster 相关定义 1, redis cluster 是什么 2,redis 集群的组成 3,集群的作用 4,集群架构图 二 Redis集群的数据分片 1,哈希槽是什么 2,哈希槽如何排布 3,Redis集…...

python实现网络爬虫
网络爬虫是一个自动从互联网上抓取数据的程序。Python有很多库可以帮助我们实现网络爬虫,其中最常用的是requests(用于发送HTTP请求)和BeautifulSoup(用于解析HTML或XML文档)。 以下是一个简单的Python网络爬虫示例&a…...
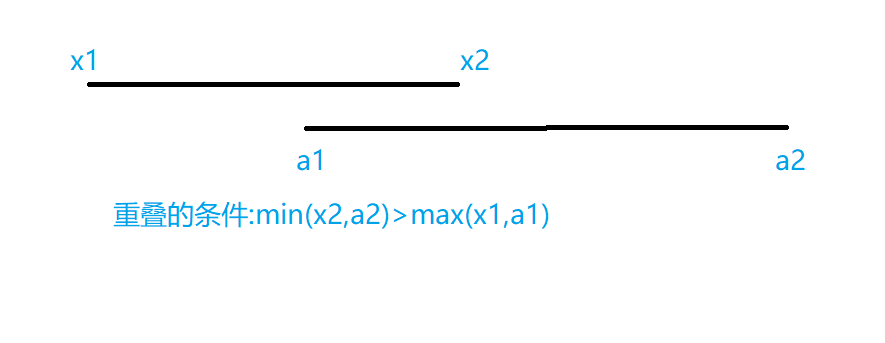
LeetCode 836. 矩形重叠
解题思路 相关代码 class Solution {public boolean isRectangleOverlap(int[] rec1, int[] rec2) {int x1 rec1[0];int y1 rec1[1];int x2 rec1[2];int y2 rec1[3];int a1 rec2[0];int b1 rec2[1];int a2 rec2[2];int b2 rec2[3];return Math.min(y2,b2)>Math.max…...
为说阿拉伯语的国家进行游戏本地化
阿拉伯语是由超过4亿人使用的语言,并且是二十多个国家的官方语言。进入这些国家的市场并非易事——虽然他们共享一种通用语言,但每个国家都有自己独特的文化,有自己的禁忌和对审查的处理方式。这就是为什么视频游戏公司长期以来都远离阿拉伯语…...

【Python系列】读取 Excel 第一列数据并赋值到指定列
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…...
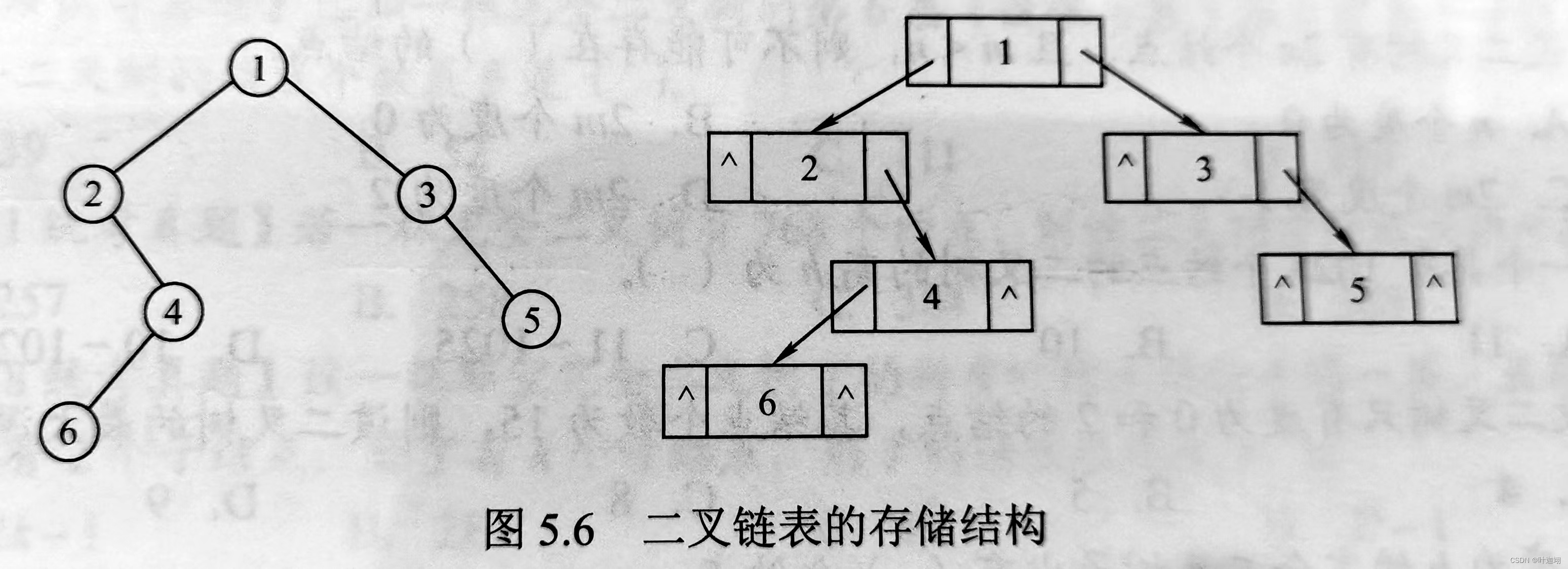
二叉树——存储结构
二叉树的存储结构 二叉树一般可以使用两种结构存储,一种是顺序结构,另一种是链式结构。 一、顺序存储 二叉树的顺序存储是指用一组连续的存储单元依次自上而下、自左至右存储完全二叉树上的结点元素,即将完全二叉树上编号为i的结点元素存储…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

论文阅读:Matting by Generation
今天介绍一篇关于 matting 抠图的文章,抠图也算是计算机视觉里面非常经典的一个任务了。从早期的经典算法到如今的深度学习算法,已经有很多的工作和这个任务相关。这两年 diffusion 模型很火,大家又开始用 diffusion 模型做各种 CV 任务了&am…...

Tauri2学习笔记
教程地址:https://www.bilibili.com/video/BV1Ca411N7mF?spm_id_from333.788.player.switch&vd_source707ec8983cc32e6e065d5496a7f79ee6 官方指引:https://tauri.app/zh-cn/start/ 目前Tauri2的教程视频不多,我按照Tauri1的教程来学习&…...

【1】跨越技术栈鸿沟:字节跳动开源TRAE AI编程IDE的实战体验
2024年初,人工智能编程工具领域发生了一次静默的变革。当字节跳动宣布退出其TRAE项目(一款融合大型语言模型能力的云端AI编程IDE)时,技术社区曾短暂叹息。然而这一退场并非终点——通过开源社区的接力,TRAE在WayToAGI等…...
