大厂面试:找出数组中第k大的数的最佳算法

一.前置条件
假如数组为a,大小为n,要找到数组a中第k大的数。
二.解决方案
1.使用任意一种排序算法(例如快速排序)将数组a进行从大到小的排序,则第n-k个数即为答案。
2.构造一个长度为k的数组,将前k个数复制过来并降序排序。然后依次将 k+1 到 n 位的数分别插入 k 长度的数组中并保持数组长度为k且降序排列。最终长度为k的数组的最后一个元素即是答案。
3.将数组的所有元素构造一个大顶堆,然后删除堆顶元素k次并重新构成大顶堆,则第k次操作后的堆顶元素即为答案。
4.用快速排序的思想不把数组元素全排序的优化算法。
1)先看一下快速排序(降序排序)的算法。
/**
快速排序主函数
a:要排序的数组
left:排序数组左边界索引
right:排序数组右边界索引
*/
public void quickSort(int a[], int left, int right) {if (left < right) {//算出基准元素索引值indexint index = partition(a, left, right);//对低于index索引的数组递归排序quickSort(a, left, index - 1);//对高于index索引的数组递归排序quickSort(a, index + 1, right);}}//算出基准元素索引值,此索引值左侧值都大于基准元素值,此索引值右侧值都小于基准元素值
public int partition(int[] num, int left, int right) {if (num == null || num.length <= 0 || left < 0 || right >= num.length) {return 0;}//获取数组基准元素的下标int prio = num[left + (right - left) / 2]; //从两端交替向中间扫描 while (left <= right) { while (num[left] > prio)left++;while (num[right] < prio)right--;if (left <= right) {//将不符合条件的元素值交换位置并继续扫描swap(num, left, right); left++;right--;}}return left;
}//交换元素
public void swap(int[] num, int left, int right) {int temp = num[left];num[left] = num[right];num[right] = temp;
}2)我们选择数组区间 a[0…n-1]的中间位置的一个元素 a[n/2]作为 pivot,对数组 a[0…n-1]进行分区,这样数组就分成了三部分,a[0…p-1]、a[p]、a[p+1…n-1]。
如果 p+1=k,那 a[p]就是要求解的答案;如果 k>p+1, 说明第 k 大元素出现在 a[p+1…n-1]区间,我们再按照上面的思路递归的在 a[p+1…n-1]这个区间内查找。同理,如果 k<p+1,那就在 a[0…p-1]区间内递归查找。
3)所以改进后的代码如下:
public int quickSortKthLargest(int a[], int left, int right, int k) {if (left < right) {//算出基准元素索引值indexint index = partition(a, left, right);//索引对应的值就是第k大的数if(index+1==k){return a[index];}//在索引左边继续查找else if(index+1>k){return quickSortKthLargest(a, left, index-1, k);} //在索引右边继续查找else{return quickSortKthLargest(a, index+1, right, k);}}else{return -1;}}
5.在Python中,我们可以使用内置的heapq库来查找数组的第k大元素。heapq库实现了一个堆数据结构,我们可以利用堆的性质来找到数组的第k大元素。
代码如下:
# 返回第k大元素
def get_kth_largest(a, k): # heapq.nlargest(k, a)会返回数组a中最大的k个元素,# 然后我们通过[-1]来取得这k个元素中的最后一个,也就是第k大的元素。return heapq.nlargest(k, a)[-1]
6.使用最小堆来查找第k大的元素。
首先构建一个空的最小堆。遍历数组a,如果堆的大小小于k,我们就把当前元素加入堆中。如果堆的大小已经达到了k,我们就比较当前元素和堆顶元素(也就是堆中的最小元素),如果当前元素大于堆顶元素,我们就把堆顶元素替换为当前元素,再重新调整最小堆结构。这样,当遍历完整个数组后,堆顶元素就是数组的第k大元素(即是大小为k的最小堆(保存了数组中的最大的k个数)的最小元素)。
代码如下:
def get_kth_largest(a, k): heap = [] for num in a: # 若最小堆大小小于k,则将元素插入最小堆if len(heap) < k: heapq.heappush(heap, num) else: # 若元素大于最小堆堆顶元素,则插入最小堆并重新排列if num > heap[0]: heapq.heapreplace(heap, num) # 堆顶元素即为数组的第k大元素return heap[0] 致力于C、C++、Java、Kotlin、Android、Shell、JavaScript、TypeScript、Python等编程技术的技巧经验分享。
若作品对您有帮助,请关注、分享、点赞、收藏、在看、喜欢。您的支持是我们为您提供帮助的最大动力。
相关文章:

大厂面试:找出数组中第k大的数的最佳算法
一.前置条件 假如数组为a,大小为n,要找到数组a中第k大的数。 二.解决方案 1.使用任意一种排序算法(例如快速排序)将数组a进行从大到小的排序,则第n-k个数即为答案。 2.构造一个长度为k的数组,将前k个数复制过来并降序…...

爬取高校专业信息的Python爬虫简介与实践
1. 介绍 在当前高校专业信息繁多的情况下,选择适合自己的专业成为了许多学生面临的挑战。为了帮助学生更好地了解各高校专业情况,我们开发了一个Python爬虫程序,用于爬取高校专业信息并保存到Excel文件中。本文将详细介绍该爬虫的实现过程以…...

redis 集群模式(redis cluster)介绍
目录 一 redis cluster 相关定义 1, redis cluster 是什么 2,redis 集群的组成 3,集群的作用 4,集群架构图 二 Redis集群的数据分片 1,哈希槽是什么 2,哈希槽如何排布 3,Redis集…...

python实现网络爬虫
网络爬虫是一个自动从互联网上抓取数据的程序。Python有很多库可以帮助我们实现网络爬虫,其中最常用的是requests(用于发送HTTP请求)和BeautifulSoup(用于解析HTML或XML文档)。 以下是一个简单的Python网络爬虫示例&a…...
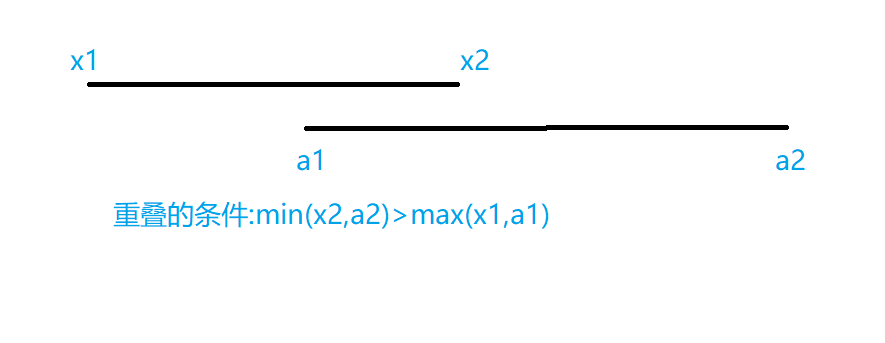
LeetCode 836. 矩形重叠
解题思路 相关代码 class Solution {public boolean isRectangleOverlap(int[] rec1, int[] rec2) {int x1 rec1[0];int y1 rec1[1];int x2 rec1[2];int y2 rec1[3];int a1 rec2[0];int b1 rec2[1];int a2 rec2[2];int b2 rec2[3];return Math.min(y2,b2)>Math.max…...
为说阿拉伯语的国家进行游戏本地化
阿拉伯语是由超过4亿人使用的语言,并且是二十多个国家的官方语言。进入这些国家的市场并非易事——虽然他们共享一种通用语言,但每个国家都有自己独特的文化,有自己的禁忌和对审查的处理方式。这就是为什么视频游戏公司长期以来都远离阿拉伯语…...

【Python系列】读取 Excel 第一列数据并赋值到指定列
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…...
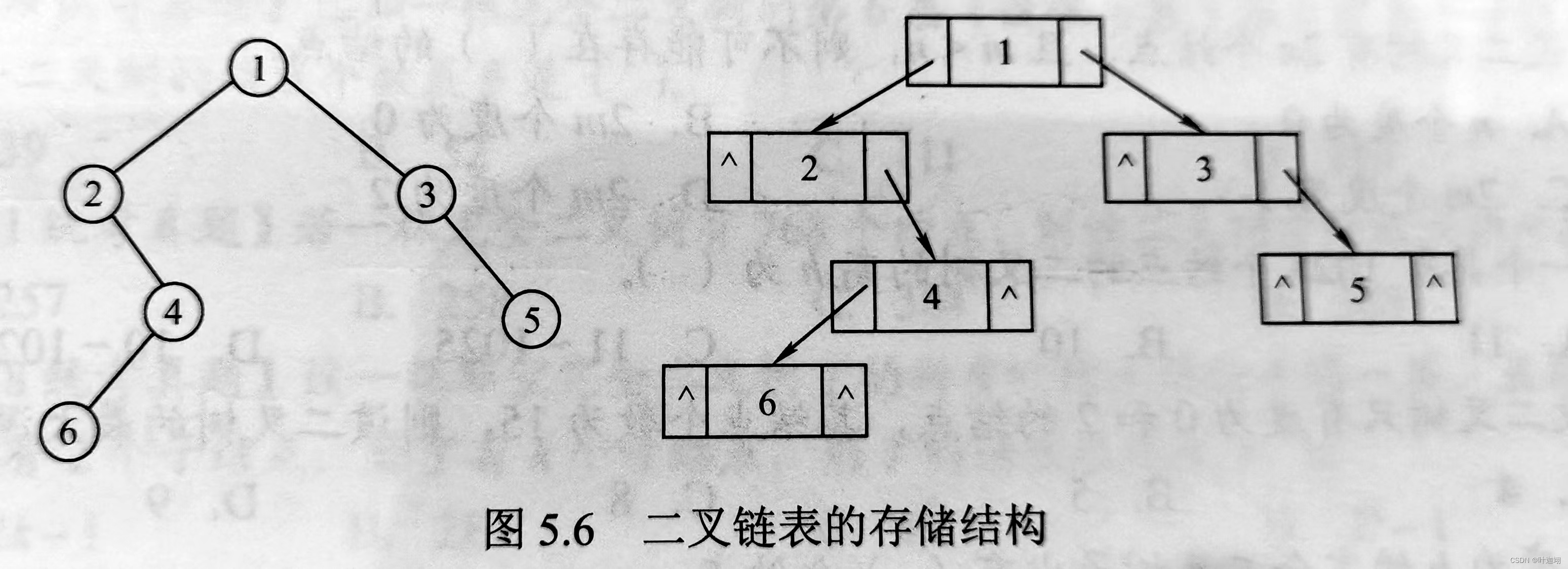
二叉树——存储结构
二叉树的存储结构 二叉树一般可以使用两种结构存储,一种是顺序结构,另一种是链式结构。 一、顺序存储 二叉树的顺序存储是指用一组连续的存储单元依次自上而下、自左至右存储完全二叉树上的结点元素,即将完全二叉树上编号为i的结点元素存储…...
LangChain - OpenGPTs
文章目录 MessageGraph 消息图认知架构AssistantsRAGChatBot 持久化配置新模型新工具astream_events总结 关键链接: OpenGPT GitHub 存储库YouTube 上的 OpenGPT 演练LangGraph:Python、JS 两个多月前,在 OpenAI 开发日之后,我们…...
-节表)
pe格式从入门到图形化显示(四)-节表
文章目录 前言一、什么是Windows PE格式节表?二、解析节表并显示1.节表数据结构以及字段描述2.节表的属性3.解析4.显示 前言 通过分析和解析Windows PE格式,并使用qt进行图形化显示 一、什么是Windows PE格式节表? PE格式的节表(…...

路由策略与路由控制之双点双向重发布(OSPF-ISIS)实验
双点双向重发布在路由协议中,特别是在OSPF(开放式最短路径优先)与IS-IS(中间系统到中间系统)等协议之间,指的是在两个协议间或者两个进程间进行路由信息共享的机制。这种机制涉及到在两个不同的协议区域使用…...
9proxy—数据采集工具全面测评
9Proxy数据采集工具Unlock the web with 9Proxy, the top residential proxy provider. Get unlimited bandwidth, affordable prices, and secure HTTPS and Socks5 configurations.https://9proxy.com/?utm_sourceblog&utm_mediumcsdn&utm_campaignyan 前言 在当今数…...
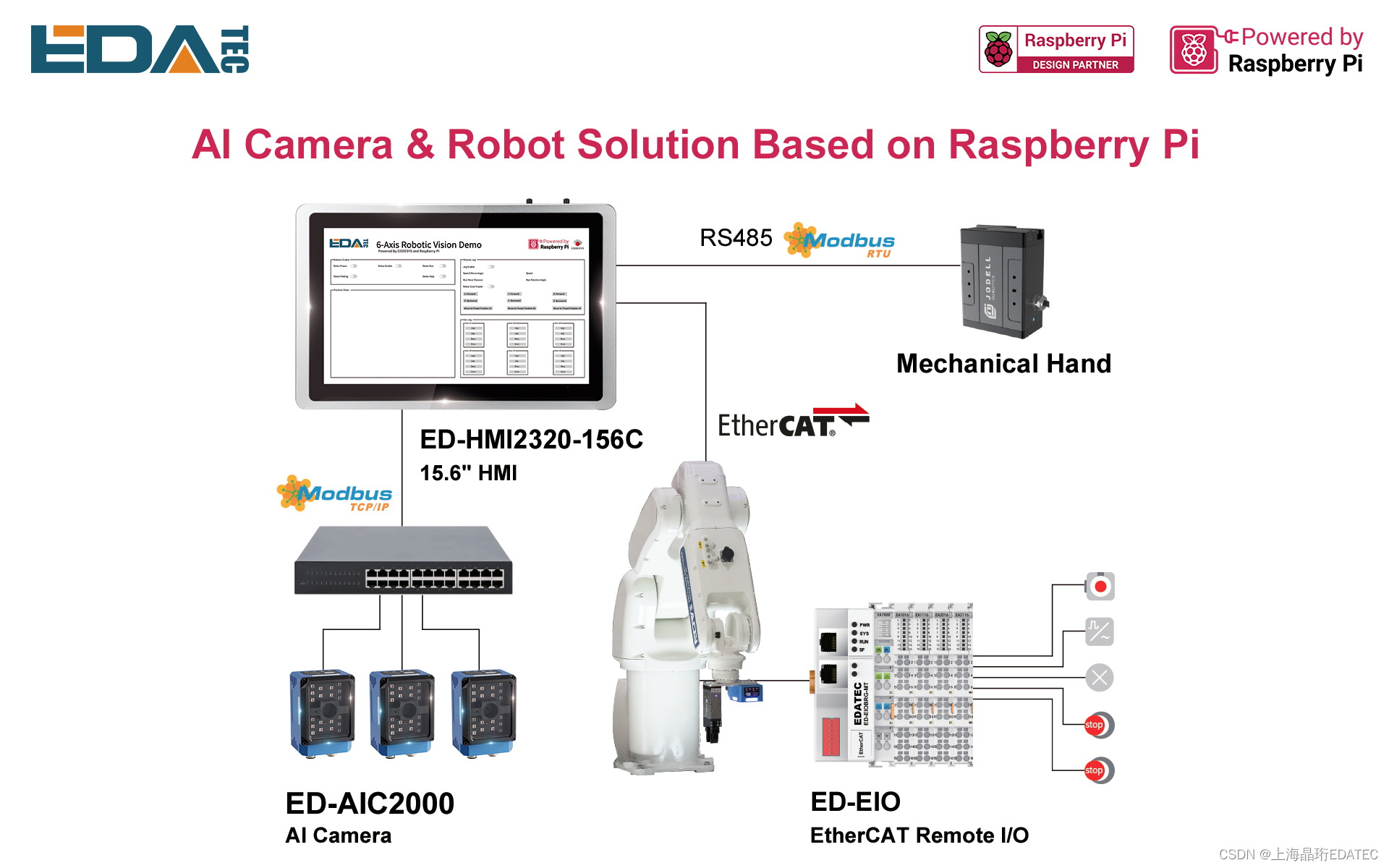
上海晶珩树莓派工业智能机械臂,亮相2024年embedded world博览会!
上海晶珩树莓派工业智能机械臂,亮相2024年embedded world博览会! 工业智能机械臂是上海晶珩(EDATEC)团队基于树莓派工业相机ED-AIC2000和树莓派工业触摸屏ED-HMI2320开发的创新应用案例。 工业智能机械臂具备卓越的定位能力&…...

蓝桥杯——求和
题目 给定 n 个整数 a1, a2,…,an,求它们两两相乘再相加的和即: Sa1a2a1a3a1ana2a3 a(n-2)*an...a(n-1)*an 输入格式 输入的第一行包含一个整数 n。 第二行包含 几 个整数 a1,a2,,an。 输出格式 输出一个整数 S,表示所…...

设计模式:责任链模式示例
责任链模式可以应用于多种场景,下面是几个不同场景的例子,每个例子都包括完整的代码。 示例1:日志处理系统 在日志处理系统中,日志消息可以根据其严重性(错误、警告、信息)被不同级别的日志处理器处理。 …...
SpringBoot快速入门笔记(4)
文章目录 一、Vue框架1、前端环境准备2、简介3、快速开始4、事件绑定 二、Vue组件化开发1、NPM2、Vue Cli3、组件化开发4、SayHello自定义组件5、Movie自定义组件 一、Vue框架 1、前端环境准备 编码工具:VSCode 依赖管理:NPM 项目构建:VueCl…...

GoPro相机使用的文件格式和频率
打开GoPro相机(以11为例),里面是一个DCIM文件夹。 DCIM是digital camera in memory 的简写,即存照片的文件夹,常见于数码相机、手机存储卡中的文件夹名字。 正常手机拍照和视频都是保存在此文件夹的。正常建议不用删,因为只要拍照…...
Redis Stack 安装部署
参考:Run Redis Stack on Docker | Redis Redis-stack 初体验_redis stack-CSDN博客 【docker】运行redis_docker run redis-stack-server requirepass-CSDN博客 Redis Stack 是一组软件套件,它主要由三部分组成。 一个是 Redis Stack Server&#x…...
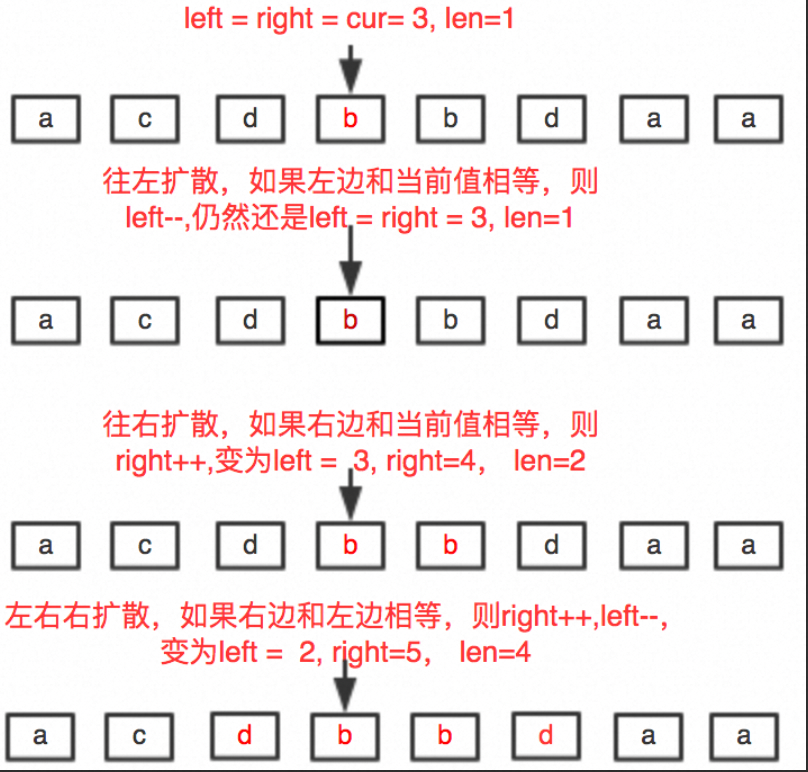
【经典算法】LeetCode 5: 最长回文子串(Java/C/Python3实现含注释说明,Medium)
目录 题目描述思路及实现方式一:动态规划法思路代码实现Java版本C语言版本Python3版本 复杂度分析 方式二:中心扩展法思路代码实现Java版本C语言版本Python3版本 复杂度分析 总结相似题目 标签(题目类型):回文串、动态规划 题目描述 给定一…...

39.Python从入门到精通—parseString 方法 Python 解析XML实例 使用xml.dom解析xml
39.Python从入门到精通—parseString 方法 Python 解析XML实例 使用xml.dom解析xml parseString 方法Python 解析XML实例使用xml.dom解析xml parseString 方法 parseString 方法是 Python 标准库中 xml.dom.minidom 模块中的一个函数,用于解析 XML 字符串并构建 DO…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...
