iOS App Store审核要求与Flutter应用的兼容性分析
本文探讨了使用Flutter开发的iOS应用能否上架,以及上架的具体流程。苹果提供了App Store作为正式上架渠道,同时也有TestFlight供开发者进行内测。合规并通过审核后,Flutter应用可以顺利上架。但上架过程可能存在一些挑战,因此可能需要专业技术人员或上架服务商的协助。
Flutter作为一种跨平台的移动应用开发框架,广受开发者欢迎。然而,对于iOS应用的上架问题,许多开发者仍然存在疑虑。本文将探讨Flutter应用在iOS上架的可行性以及具体步骤,为开发者提供指导和建议。
📚 正文
-
Flutter应用上架流程
-
审核标准: Flutter应用上架的关键在于符合苹果的审核标准。这包括但不限于应用的内容、功能、用户体验和设计等方面。
-
TestFlight: 开发者可以使用苹果提供的TestFlight进行内测,这是一个相对宽松的审核环境,可以帮助开发者发现并解决潜在问题。
-
App Store: 一旦应用通过内测并完善,开发者可以将应用提交至App Store进行正式上架。苹果会对应用进行严格审核,确保其质量和安全性。
-
-
需要注意的问题
-
性能优化: Flutter应用在iOS上的性能优化尤为重要。确保应用流畅、稳定运行,避免出现卡顿和闪退等问题。
-
UI/UX设计: 苹果对应用的UI/UX设计要求较高,开发者需要遵循苹果的设计指南,确保应用界面美观、易用。
-
设备适配: Flutter应用需要适配不同的iOS设备,包括iPhone和iPad等,确保在不同尺寸和分辨率的屏幕上都能正常显示和使用。
-
APP上架操作步骤
开发者需要将App成功上架至App Store,并通过各大安卓应用市场等渠道进行推广。使用工具如appuploader能够帮助进行证书制作和IPA上传,提高上架效率。
📝 总结
Flutter应用在iOS上架是完全可行的,只要开发者合规并通过了苹果的审核。TestFlight提供了一个内测的平台,可以帮助开发者在正式上架之前发现和解决问题。在上架过程中,开发者需要注意性能优化、UI/UX设计和设备适配等方面,以确保应用的质量和用户体验。
相关文章:

iOS App Store审核要求与Flutter应用的兼容性分析
本文探讨了使用Flutter开发的iOS应用能否上架,以及上架的具体流程。苹果提供了App Store作为正式上架渠道,同时也有TestFlight供开发者进行内测。合规并通过审核后,Flutter应用可以顺利上架。但上架过程可能存在一些挑战,因此可能…...

javaScript常见对象方法总结
1,object.assign() 用于合并对象的属性。它可以将一个或多个源对象的属性复制到目标对象中,实现属性的合并。 语法 Object.assign(target, ...sources); 1,target:目标对象,将属性复制到该对象中。 2,sources:一个…...

使用Java流API构建树形结构数据
简介: 在实际开发中,构建树状层次结构是常见需求,如组织架构、目录结构或菜单系统。本教案通过解析给定的Java代码,展示如何使用Java 8 Stream API将扁平化的菜单数据转换为具有层级关系的树形结构。 1. 核心类定义 - Menu Data…...

蓝桥杯备考
1.1 输入输出 cin/cout scanf/printf 万能头文件 #include<bits/stdc.h> cin/cout 速度相对慢,需要关同步,代码如下 #include<bits/stdc.h> using namespace std; int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int x,y;cin>>x…...

Linux云计算之Linux基础1——操作系统理论基础
目录 1、UNIX 的诞生和广泛使用 2、CPU 架构类型 3、CPU 指令 4、计算机程序设计和执行过程 5、操作统OS 6、编程层次 7、程序的内部运行接口 8、UI程序接口(人机交互接口) 9、程序的运行模式: 10、POSIX:可移植操作系统规范 11、计算机开源领域 12、Li…...

大模型从入门到应用——OpenAI基础调用
摘要:这是OpenAI的基本调用,通过文章了解大模型的一个基础使用 1. 调用说明 在大型语言模型(LLM)的应用中,OpenAI的基础调用是入门的关键一步。通过调用OpenAI的API,我们可以利用其强大的语言处理能力&am…...
前端学习<三>CSS进阶——0102-CSS布局样式
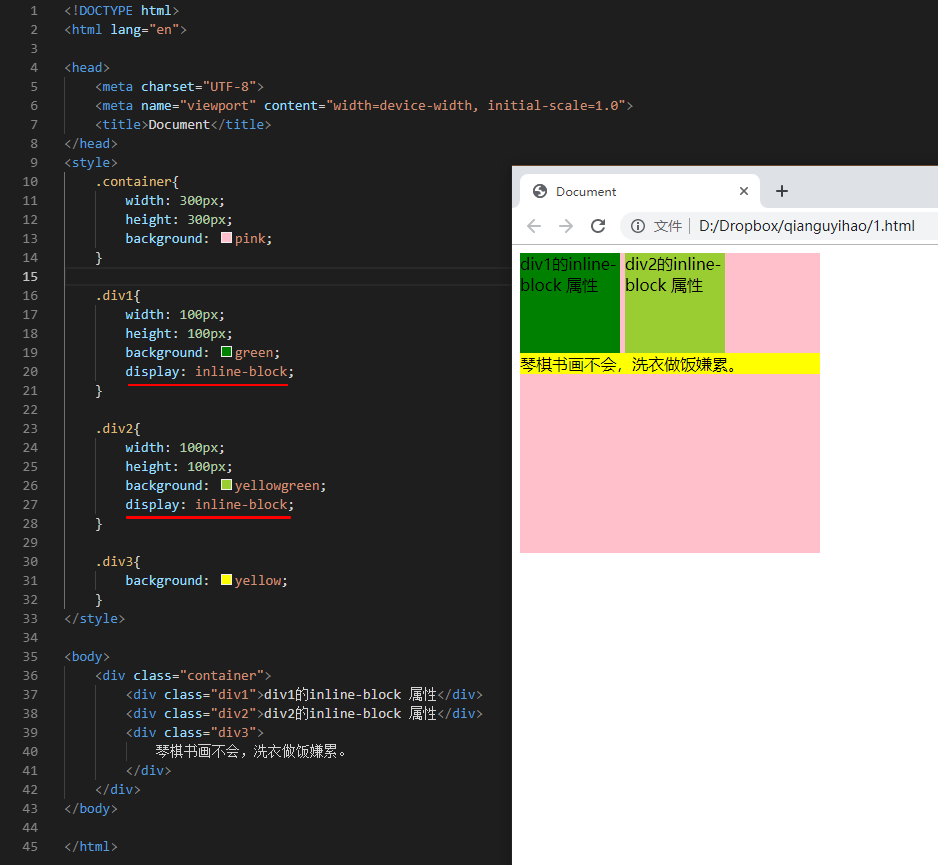
前言 css 进阶的主要内容如下。 1、css 非布局样式 html 元素的分类和特性 css 选择器 css 常见属性(非布局样式) 2、css 布局相关 css 布局属性和组合解析 常见布局方案 三栏布局案例 3、动画和效果 属于 css 中最出彩的内容。 多背景多投影特…...
关于51单片机TMOD定时器的安全配置
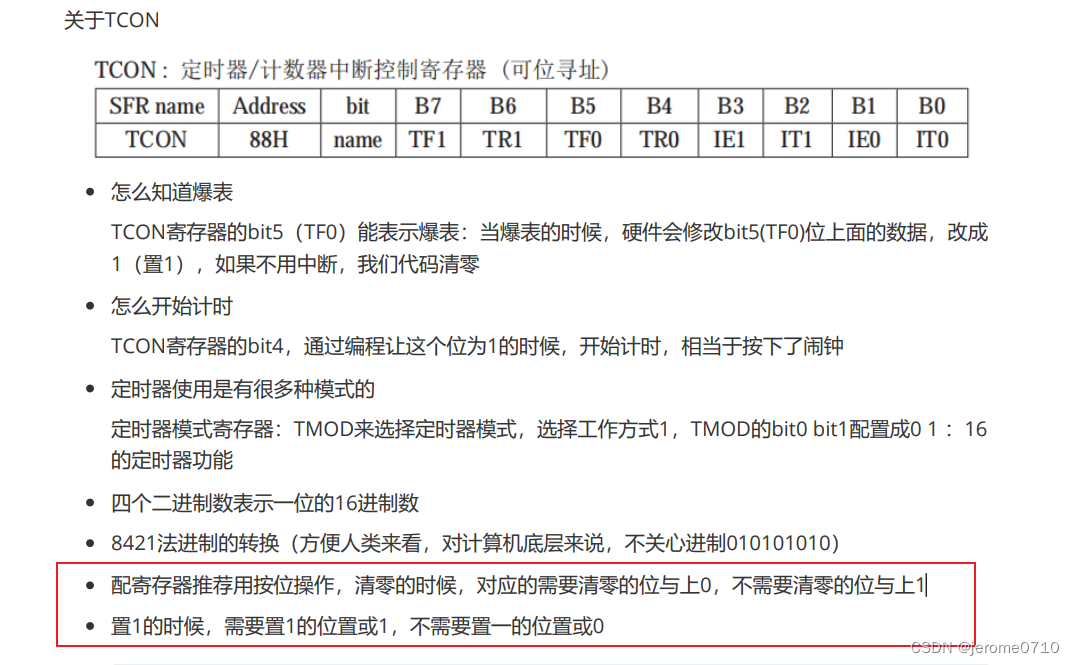
定时器介绍: -------------------------------------------------------------------------------------------------------------------------- 首先配置的是控制寄存器 TCON 说直白点,这个寄存器就是用来计数的,打开计时器,关…...

Unity 主线程和其他线程之间的数据访问
在Unity中,主线程和其他线程之间的数据访问需要小心处理,因为在多线程环境下,不当的数据访问可能导致竞争条件和数据不一致性。 在Unity中,主线程通常用于处理用户输入、更新游戏逻辑和渲染。其他线程通常用于执行耗时的计算、加…...

电商系列之风控安全
> 插:AI时代,程序员或多或少要了解些人工智能,前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站。 坚持不懈,越努力越幸运,大家…...

计算机网络针对交换机的配置
实验 目的 交换机的基本配置,交换机VLAN配置 实验条件 Windows,Cisco packet tracer 实验 内容 交换机的基本配置,交换机VLAN配置 实验 过程 一、交换机的基本配置 进入特权模式 Switch>enable 进入配置模式 Switch#configure ter…...
Python爬虫之分布式爬虫
分布式爬虫 1.详情介绍 分布式爬虫是指将一个爬虫任务分解成多个子任务,在多个机器上同时执行,从而加快数据的抓取速度和提高系统的可靠性和容错性的技术。 传统的爬虫是在单台机器上运行,一次只能处理一个URL,而分布式爬虫通过将…...

服务器硬件基础知识解析
导言 在当今信息化时代,服务器扮演着至关重要的角色,它们是存储、处理和传输数据的关键设备。本文将介绍服务器硬件的基础知识,包括服务器的组成部分、硬件选型和性能评估等内容,旨在帮助读者更好地理解和应用服务器技术。 服务…...

【芯片设计- RTL 数字逻辑设计入门 1.1 -- Verdi 使用入门介绍 1】
请阅读【芯片设计 RTL 数字逻辑设计扫盲 】 文章目录 Verdi 介绍Verdi 特点和功能Verdi 基本操作Verdi -elab与-dbdir区别-elab 参数介绍-dbdir 参数介绍区别总结Verdi 介绍 Verdi 是由Synopsys公司开发的一款业界领先的自动化电子设计自动化(EDA)工具,主要用于功能验证和调…...
ssm034学生请假系统+jsp
学生请假系统设计与实现 摘 要 现代经济快节奏发展以及不断完善升级的信息化技术,让传统数据信息的管理升级为软件存储,归纳,集中处理数据信息的管理方式。本学生请假系统就是在这样的大环境下诞生,其可以帮助管理者在短时间内处…...

Leetcode 165. 比较版本号
给你两个版本号 version1 和 version2 ,请你比较它们。 版本号由一个或多个修订号组成,各修订号由一个 ‘.’ 连接。每个修订号由 多位数字 组成,可能包含 前导零 。每个版本号至少包含一个字符。修订号从左到右编号,下标从 0 开…...

LeetCode-279. 完全平方数【广度优先搜索 数学 动态规划】
LeetCode-279. 完全平方数【广度优先搜索 数学 动态规划】 题目描述:解题思路一:Python 动态规划五部曲(完全平方数就是物品(可以无限件使用),凑个正整数n就是背包,问凑满这个背包最少有多少物品…...
rust项目组织结构和集成测试举例
概述 在学习rust的过程中,当项目结构略微复杂的时候,写集成测试的时候发现总是不能引用项目中的代码,导致编写测试用例失败。查阅了教程,一般举例都很简单。查阅了谷歌和百度以及ai,也没有找到满意的答案。这里记录一…...

软件文档交付清单(直接套用合集)
软件文档交付清单是指在软件开发项目完成后,开发团队需要准备的一份详细清单,用于确保交付的软件产品符合客户需求并达到预期的质量标准。以下是软件文档交付清单中可能包含的一些关键要素 软件开发文档:这包括需求文档、设计文档、测试文档等…...
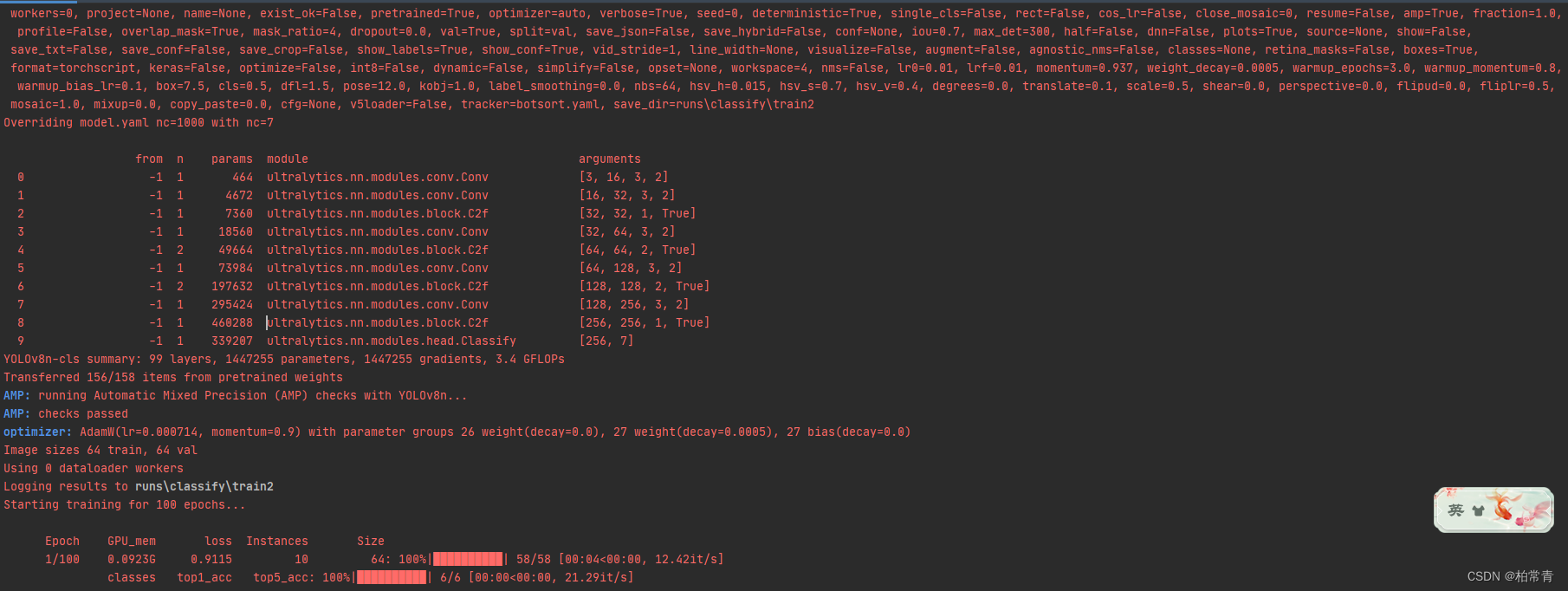
ModuleNotFoundError: No module named ‘ultralytics.utils‘
项目场景he 问题描述 提示:这里简述项目相关背景: model YOLO(modelr./yolov8m-cls.pt) 加载预训练模型时报错。 ModuleNotFoundError: No module named ultralytics.utils warning: bug: 原因分析: 很可能是提前下载的预训练模型出了…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...

软件工程 期末复习
瀑布模型:计划 螺旋模型:风险低 原型模型: 用户反馈 喷泉模型:代码复用 高内聚 低耦合:模块内部功能紧密 模块之间依赖程度小 高内聚:指的是一个模块内部的功能应该紧密相关。换句话说,一个模块应当只实现单一的功能…...

【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅!
【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅! 🌱 前言:一棵树的浪漫,从数组开始说起 程序员的世界里,数组是最常见的基本结构之一,几乎每种语言、每种算法都少不了它。可你有没有想过,一组看似“线性排列”的有序数组,竟然可以**“长”成一棵平衡的二…...
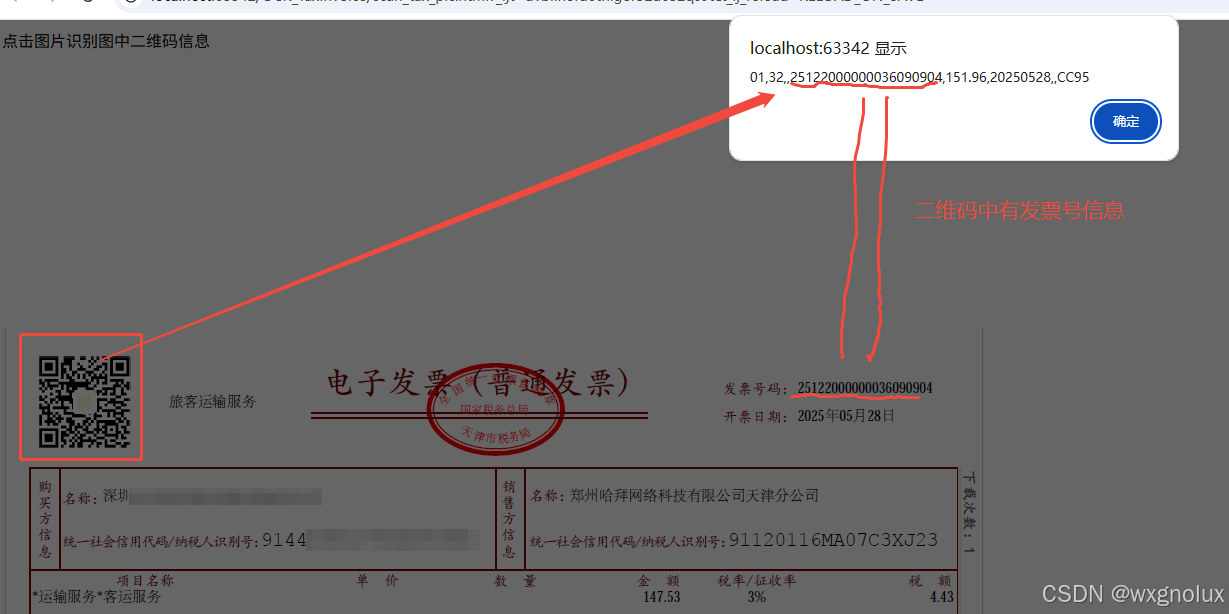
网页端 js 读取发票里的二维码信息(图片和PDF格式)
起因 为了实现在报销流程中,发票不能重用的限制,发票上传后,希望能读出发票号,并记录发票号已用,下次不再可用于报销。 基于上面的需求,研究了OCR 的方式和读PDF的方式,实际是可行的ÿ…...
