第十二届蓝桥杯大赛软件赛省赛C/C++大学B组
第十二届蓝桥杯大赛软件赛省赛C/C++ 大学 B 组
文章目录
- 第十二届蓝桥杯大赛软件赛省赛C/C++ 大学 B 组
- 1、空间
- 2、卡片
- 3、直线
- 4、货物摆放
- 5、路径
- 6、时间显示
- 7、砝码称重
- 8、杨辉三角形
- 9、双向排序
- 10、括号序列
1、空间

1MB = 1024KB
1KB = 1024byte
1byte=8bit
// cout<<"256*1024*1024/4"; // 记住 1024 即可
2、卡片


往简单的讲就是一个排列组合的问题,因为可以选自身,所以n张卡片最多有 n + C2n中方案。
我们可以把它想象成一个开口向上的二次函数然后根据x去求最小的y值。
#include<iostream>
#define ll long long
using namespace std;
ll n,k;
int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>n;// (x^2+x)/2 = n// 2n = x^2+x// x^2+x-2n=0 求xfor(ll i=1;i<=1e9;i++){if(i*i+i>=2*n){cout<<i;return 0; }} return 0;
}
3、直线

#include<iostream>
#include<set>
#define pii pair<double,double>
#define ll long long
using namespace std;
int x=20,y=21;
set<pii> st;
void check(int x1,int y1,int x2,int y2){if(x1==x2||y1==y2)return;double k=(y2-y1)*1.0/(x2-x1);// y1=k*x1+b y2=k*x2+b// k=(y2-y1)/(x2-x1)替代即可算出b=(x2*y1-x1*y2)/(x2-x1) double b=(x2*y1-x1*y2)*1.0/(x2-x1);st.insert({k,b});
}
int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);for(int i=0;i<y;i++){for(int j=0;j<x;j++){for(int k=0;k<y;k++){for(int t=0;t<x;t++){check(j,i,t,k);}}}}cout<<st.size()+x+y; return 0;
}
4、货物摆放

先去找到这个数的所有因子,再去枚举这些因可能成为的结果。最后计算这些结果。
#include<iostream>
#include<cmath>
#define ll long long
using namespace std;
ll n = 2021041820210418;
ll a[50001],cnt=0;
int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);for(int i=1;i<=sqrt(n);i++){if(n%i==0){a[++cnt]=i;if(i*i!=n)a[++cnt]=n/i;}}int res=0;for(int l=1;l<=cnt;l++)for(int w=1;w<=cnt;w++)for(int h=1;h<=cnt;h++)if(a[l]*a[w]*a[h]==n)res++;cout<<res;return 0;
}
5、路径

#include<iostream>
#define ll long long
using namespace std;
const int n = 2025;
//ll d[n][n];
ll INF = 1e17;
// 循环遍历超时,辗转相除法高效
int gcd(int a,int b){if(a%b==0)return b;return gcd(b,a%b);
}
int lcm(int a, int b){return a / gcd(a, b) * b;}
//void floyd(){
// for(int k=1;k<=n;k++)
// for(int i=1;i<=n;i++)
// for(int j=1;j<=n;j++)
// if(d[i][k]!=INF&&d[k][j]!=INF)d[i][j]=min(d[i][j],d[i][k]+d[k][j]);
//}int d[n];
int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);for(int i=0;i<n;i++)d[i]=INF;d[1]=0;for(int i=1;i<n;i++)for(int j=i+1;j<n&&j-i<=21;j++){d[j]=min(d[j],lcm(i,j)+d[i]);}cout<<d[2021];return 0;
}
6、时间显示


时间换算,思维创新。
#include<iostream>
#define ll long long
using namespace std;
ll n,h,m,s;
int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>n;n=n/1000;//舍弃毫秒 1s = 1000ms n=n%(24*60*60);// 一天24小时 h=n/3600;m=(n-h*3600)/60;s=n-3600*h-60*m;if(h<10){cout<<"0"<<h<<":";}else{cout<<h<<":";}if(m<10){cout<<"0"<<m<<":";}else{cout<<m<<":";}if(s<10){cout<<"0"<<s;}else{cout<<s;}return 0;
}
7、砝码称重



#include<iostream>
#include<queue>
#include<cmath>
#include<cstring>
using namespace std;
const int N = 1e5+10;
queue<int> q;
int n,w,cnt;
bool ans[N];
int main(){memset(ans,0,sizeof(ans));cin>>n;q.push(0);for(int i=0;i<n;i++){cin>>w;queue<int> tmp_q;while(!q.empty()){int x=q.front();q.pop();if(ans[x+w]==false){ans[x+w]=true;cnt++;tmp_q.push(x+w);}if(ans[abs(x-w)]==false){ans[abs(x-w)]=true;cnt++;tmp_q.push(abs(x-w));}tmp_q.push(x);}q=tmp_q;}cout << cnt-1;//为0的情况不要return 0;
}
8、杨辉三角形


只会写朴素算法,优化的算法,还没看懂。。。。。
这个只能过40%。
#include<iostream>
#define ll long long
using namespace std;
const int N = 2e3+5;
int dp[N][N],n;
int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>n;if(n==1){cout<<"1";return 0;} dp[1][1]=dp[2][1]=dp[2][2]=1;for(int i=3;i<N-1;i++){for(int j=1;j<=i;j++){if(j==1||j==i){dp[i][j]=1;}else{dp[i][j]=dp[i-1][j]+dp[i-1][j-1];}if(dp[i][j]==n){// (a1+an)/2 a1=i,an=i-1,多出来的 + j cout<<i*(i-1)/2+j;return 0;}}}return 0;
}
9、双向排序


直接暴力截决。只能过60%。
#include<iostream>
#include<algorithm>
#include<vector>
#define ll long long
using namespace std;
int n,m;
vector<int> v;
bool cmp(int a,int b){return a>b;
}
int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>n>>m;for(int i=1;i<=n;i++)v.push_back(i);for(int i=1;i<=m;i++){int p,q;cin>>p>>q;if(p==0)sort(v.begin(),v.begin()+q,cmp);else sort(v.begin()+q-1,v.end());}for(const auto& x:v)cout<<x<<' ';return 0;
}
10、括号序列


这题没看懂。。。
相关文章:

第十二届蓝桥杯大赛软件赛省赛C/C++大学B组
第十二届蓝桥杯大赛软件赛省赛C/C 大学 B 组 文章目录 第十二届蓝桥杯大赛软件赛省赛C/C 大学 B 组1、空间2、卡片3、直线4、货物摆放5、路径6、时间显示7、砝码称重8、杨辉三角形9、双向排序10、括号序列 1、空间 1MB 1024KB 1KB 1024byte 1byte8bit // cout<<"2…...
,秒挂。。。。)
面了钉钉搜广增算法岗(暑期实习),秒挂。。。。
节前,我们星球组织了一场算法岗技术&面试讨论会,邀请了一些互联网大厂朋友、参加社招和校招面试的同学,针对算法岗技术趋势、大模型落地项目经验分享、新手如何入门算法岗、该如何准备、面试常考点分享等热门话题进行了深入的讨论。 汇总…...

前端实现流文件下载的完整指南
在现代Web开发中,经常会遇到需要从服务器下载文件的情况。有时候这些文件是事先存储好的,可以通过简单的URL链接直接下载;但有时候,我们需要从数据流中动态生成文件并将其提供给用户。本篇博客将介绍如何在前端实现流文件下载的完…...

Kotlin:常用标准库函数(let、run、with、apply、also)
一、let 扩展函数 Kotlin标准库函数let可用于范围确定和空检查。当调用对象时,let执行给定的代码块并返回其最后一个表达式的结果。对象可以通过引用(默认情况下)或自定义名称在块中访问。 let扩展函数源码 let.kt文件代码 fun main() {println("isEmpty $is…...

雷军给年轻人的五点建议
前言 拿来激励自己,没事就看一看,给自己高一点的要求. 致刚入门的程序员五点建议 每个IT企业,尤其是初创企业,非常苦恼:找不到好的程序员。现在大学、软件学院及各种培训机构,每年培养几十万的程序员,毕业的每个人都…...

Unity DOTS物理引擎的核心分析与详解
最近DOTS发布了正式的版本,同时基于DOTS的理念实现了一套高性能的物理引擎,今天我们来给大家分享和介绍一下这个物理引擎的使用。 Unity.Physics的设计哲学 Unity.Physics是基于DOTS设计思想的一个高性能C#物理引擎的实现, 包含了物理刚体的迭代计算与碰撞检测等查…...

C++ //练习 12.4 在我们的check函数中,没有检查i是否大于0。为什么可以忽略这个检查?
C Primer(第5版) 练习 12.4 练习 12.4 在我们的check函数中,没有检查i是否大于0。为什么可以忽略这个检查? 环境:Linux Ubuntu(云服务器) 工具:vim 解释 size_type类型是无符号整…...
达梦备份与恢复
达梦备份与恢复 基础环境 操作系统:Red Hat Enterprise Linux Server release 7.9 (Maipo) 数据库版本:DM Database Server 64 V8 架构:单实例1 设置bak_path路径 --创建备份文件存放目录 su - dmdba mkdir -p /dm8/backup--修改dm.ini 文件…...
iOS App Store审核要求与Flutter应用的兼容性分析
本文探讨了使用Flutter开发的iOS应用能否上架,以及上架的具体流程。苹果提供了App Store作为正式上架渠道,同时也有TestFlight供开发者进行内测。合规并通过审核后,Flutter应用可以顺利上架。但上架过程可能存在一些挑战,因此可能…...

javaScript常见对象方法总结
1,object.assign() 用于合并对象的属性。它可以将一个或多个源对象的属性复制到目标对象中,实现属性的合并。 语法 Object.assign(target, ...sources); 1,target:目标对象,将属性复制到该对象中。 2,sources:一个…...

使用Java流API构建树形结构数据
简介: 在实际开发中,构建树状层次结构是常见需求,如组织架构、目录结构或菜单系统。本教案通过解析给定的Java代码,展示如何使用Java 8 Stream API将扁平化的菜单数据转换为具有层级关系的树形结构。 1. 核心类定义 - Menu Data…...

蓝桥杯备考
1.1 输入输出 cin/cout scanf/printf 万能头文件 #include<bits/stdc.h> cin/cout 速度相对慢,需要关同步,代码如下 #include<bits/stdc.h> using namespace std; int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int x,y;cin>>x…...

Linux云计算之Linux基础1——操作系统理论基础
目录 1、UNIX 的诞生和广泛使用 2、CPU 架构类型 3、CPU 指令 4、计算机程序设计和执行过程 5、操作统OS 6、编程层次 7、程序的内部运行接口 8、UI程序接口(人机交互接口) 9、程序的运行模式: 10、POSIX:可移植操作系统规范 11、计算机开源领域 12、Li…...

大模型从入门到应用——OpenAI基础调用
摘要:这是OpenAI的基本调用,通过文章了解大模型的一个基础使用 1. 调用说明 在大型语言模型(LLM)的应用中,OpenAI的基础调用是入门的关键一步。通过调用OpenAI的API,我们可以利用其强大的语言处理能力&am…...
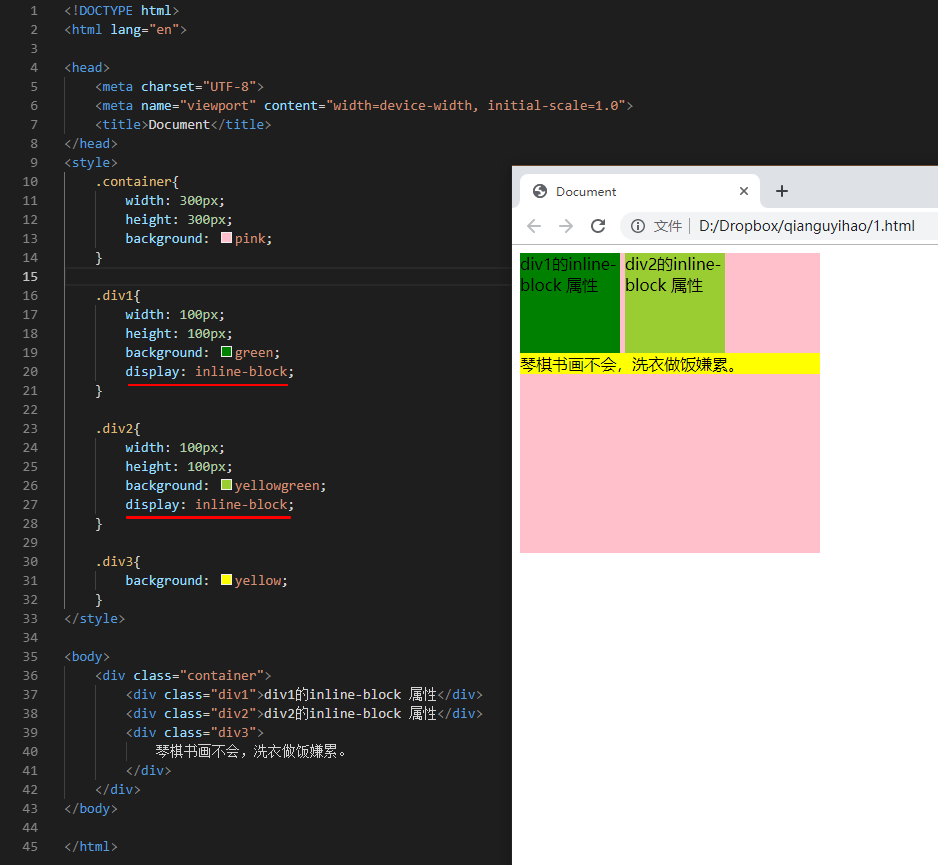
前端学习<三>CSS进阶——0102-CSS布局样式
前言 css 进阶的主要内容如下。 1、css 非布局样式 html 元素的分类和特性 css 选择器 css 常见属性(非布局样式) 2、css 布局相关 css 布局属性和组合解析 常见布局方案 三栏布局案例 3、动画和效果 属于 css 中最出彩的内容。 多背景多投影特…...
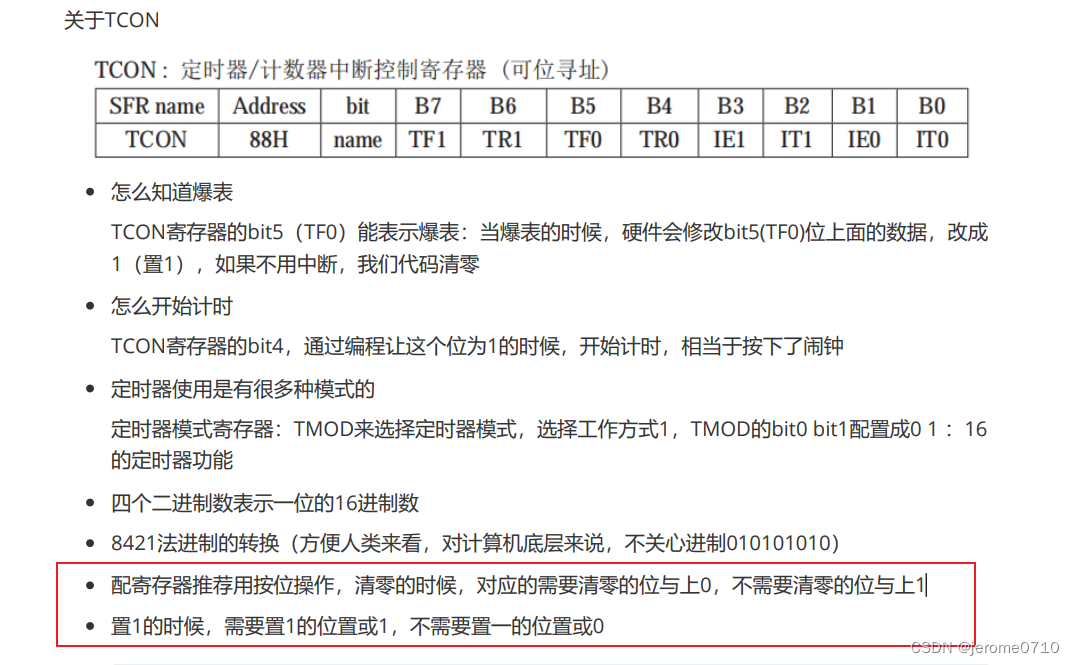
关于51单片机TMOD定时器的安全配置
定时器介绍: -------------------------------------------------------------------------------------------------------------------------- 首先配置的是控制寄存器 TCON 说直白点,这个寄存器就是用来计数的,打开计时器,关…...

Unity 主线程和其他线程之间的数据访问
在Unity中,主线程和其他线程之间的数据访问需要小心处理,因为在多线程环境下,不当的数据访问可能导致竞争条件和数据不一致性。 在Unity中,主线程通常用于处理用户输入、更新游戏逻辑和渲染。其他线程通常用于执行耗时的计算、加…...

电商系列之风控安全
> 插:AI时代,程序员或多或少要了解些人工智能,前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站。 坚持不懈,越努力越幸运,大家…...

计算机网络针对交换机的配置
实验 目的 交换机的基本配置,交换机VLAN配置 实验条件 Windows,Cisco packet tracer 实验 内容 交换机的基本配置,交换机VLAN配置 实验 过程 一、交换机的基本配置 进入特权模式 Switch>enable 进入配置模式 Switch#configure ter…...
Python爬虫之分布式爬虫
分布式爬虫 1.详情介绍 分布式爬虫是指将一个爬虫任务分解成多个子任务,在多个机器上同时执行,从而加快数据的抓取速度和提高系统的可靠性和容错性的技术。 传统的爬虫是在单台机器上运行,一次只能处理一个URL,而分布式爬虫通过将…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...
