杨辉三角形(蓝桥杯,acwing)
题目描述:
下面的图形是著名的杨辉三角形:
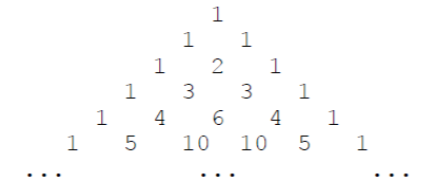
如果我们按从上到下、从左到右的顺序把所有数排成一列,可以得到如下数列:
1, 1, 1, 1, 2, 1, 1, 3, 3, 1, 1, 4, 6, 4, 1, ...
给定一个正整数 N,请你输出数列中第一次出现 N 是在第几个数?
输入格式:
输入一个整数 N。
输出格式:
输出一个整数代表答案。
数据范围:
对于 20% 的评测用例,1≤N≤10;
对于所有评测用例,1≤N≤1e9。
输入样例:
6
输出样例:
13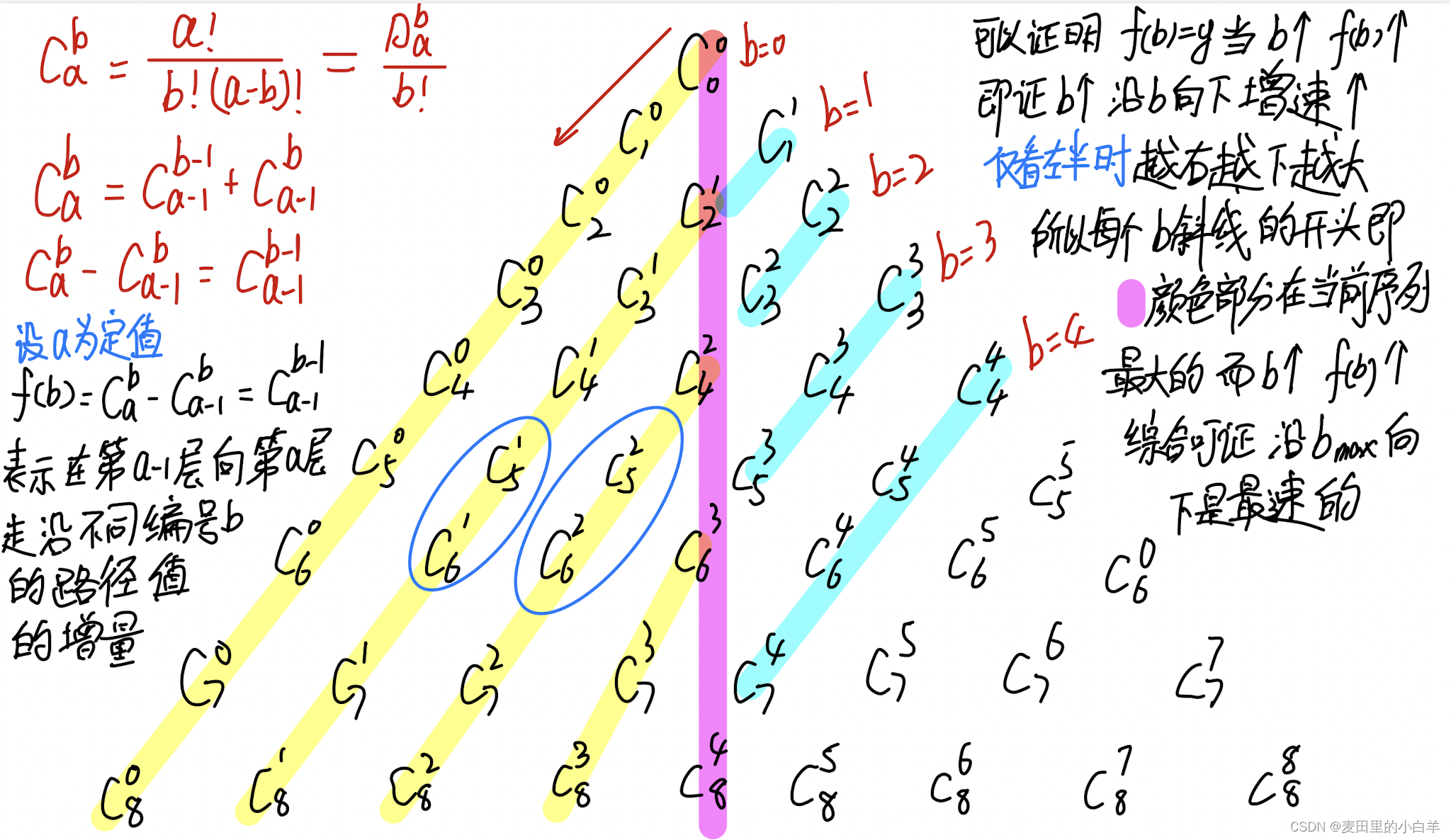
这个图是来自acwing的东风祝酒的图片
分析步骤:
第一:理清思路:
-
众所周知,杨辉三角中华瑰宝,他这个三角型是对称的,如果我们要求出哪个点是第一次出现的,那么一定是在这个三角形的左边!我们可以把右半部分删掉,完全不用考虑。这是本题目第一个特点。
-
现在我们再斜着看一看,把斜着的看做一个序列。第一行数坐标就是(0,0),第二行从左到右就是(1,0),(1,1).....以此类推。我们再看到中间紫色的这一列数值永远就是C2k^k并且永远是这个数最大,我们就可以从这个数开始找起。而且题目中说到了N最大就是1e9,那么C34^17>1e9 ; C32^16<1e9。所以我只需要找前面16个斜行就行了。这是本题的第二个特点。
-
我们现在想想,如果一个一个去找的话速度太慢了。因为序列的单调的这一眼就能看出来,而且我们需要找一个特定的,在这个值的左边就会太小了,在这个值的右边就会太大了,就可以将其分为两个部分。这就符合了我们二分的特点,因此我们直接从中间对称轴倒序二分找起即可!这就是本题的第三个特点。
-
大家一定要好好看看这图,仔细去理解!!
第二:书写主函数,构建整体框架:
-
因为我们分析过了我们只需要枚举前16行就可以了,那么我们倒序枚举,检查一下这一行是不是我们想要的,是的话就代表找到了,就break退出。
int main()
{cin >> n;for (int k = 16; ; k -- )if (check(k))break;return 0;
}第三:书写check函数:
-
现在我们就入了其中的一个序列进行检查,运用二分的方法去查找。
-
首先我们要确定二分的左节点和右节点,所以我们定义LL l = k * 2, r = n;为什么这么定义呢?因为:在一个序列之中我们最小的值是上图中紫色的那一些数,这些数的特点是C2k^k,所以定义他们为最小的左边界节点,那么右边界节点就应该是最大的那个数字了,但是我们的杨辉三角是无穷的所以我们应该只需要找到题目给出的那个数字就可以了,那么这个数一定会在Cn^1的这个地方出现,因为这个值就是N。所以我们把右边界定义为n。
-
如果l比r都要大就直接返回false不可能在这一行。因为这个数一定比这一序列的第一个数要小,就代表答案的位置在更靠前的序列之中。
-
进入while循环,计算我们的mid值计算我们的Cmid^k让这个数和n比较大小。如果这个数比n要大或等于的话就代表答案有可能在mid左边也就是更小的那一边,所以我们把r赋值给mid。反之答案比n更小的话,那么答案一定在mid的右边也就是更大的一边,就让mid+1赋值给l。
-
经过了一轮的while循环判断之后,再去计算一下Cr^k看看和答案是否一致,如果不一致就是错
-
最终输出位置即可。
bool check(int k)
{LL l = k * 2, r = n;if (l > r) return false;while (l < r){LL mid = l + r >> 1;if (C(mid, k) >= n) r = mid;else l = mid + 1;}if (C(r, k) != n) return false;cout << r * (r + 1) / 2 + k + 1 << endl;return true;
}第四:书写计算组合数的函数:
-
我们计算组合数直接暴力做就可以,利用双指针一起去求解。
LL C(int a, int b)
{LL res = 1;for (int i = a, j = 1; j <= b; i --, j ++ ){res = res * i / j;if (res > n) return res;}return res;
}代码:
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;typedef long long LL;int n;LL C(int a, int b)
{LL res = 1;for (int i = a, j = 1; j <= b; i --, j ++ ){res = res * i / j;if (res > n) return res;}return res;
}bool check(int k)
{LL l = k * 2, r = n;if (l > r) return false;while (l < r){LL mid = l + r >> 1;if (C(mid, k) >= n) r = mid;else l = mid + 1;}if (C(r, k) != n) return false;cout << r * (r + 1) / 2 + k + 1 << endl;return true;
}int main()
{cin >> n;for (int k = 16; ; k -- )if (check(k))break;return 0;
}相关文章:

杨辉三角形(蓝桥杯,acwing)
题目描述: 下面的图形是著名的杨辉三角形: 如果我们按从上到下、从左到右的顺序把所有数排成一列,可以得到如下数列: 1, 1, 1, 1, 2, 1, 1, 3, 3, 1, 1, 4, 6, 4, 1, ... 给定一个正整数 N,请你输出数列中第一次出现…...

计算系数(acwing,数论)
题目描述: 给定一个多项式 (axby)^k,请求出多项式展开后 x^n*y^m 项的系数。 输入格式: 共一行,包含 5 个整数,分别为 a,b,k,n,m,每两个整数之间用一个空格…...
阿里面试题二
实在是太长了 重新开一篇吧 dubbo 服务暴露 Dubbo——服务调用、服务暴露、服务引用过程 - 简书 这两篇文章写的是极好 我现在查得资源强的可怕朋友们 服务降级 MockClusterInvoker 负载均衡策略 容错机制在哪里实现的源码 通信 NIO、BIO区别,NIO解决了什么…...
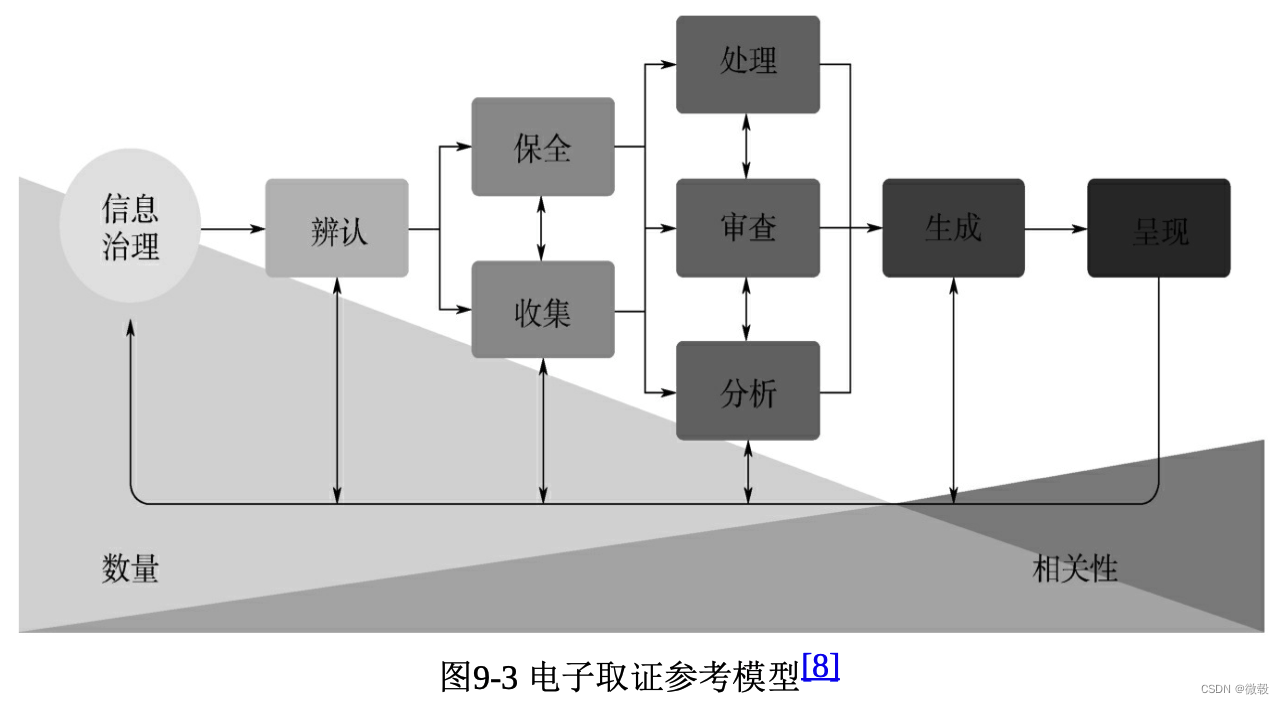
第9章 文件和内容管理
思维导图 9.1 引言 文件和内容管理是指针对存储在关系型数据库之外的数据和信息的采集、存储、访问和使用过程的管理。它的重点在于保持文件和其他非结构化或半结构化信息的完整性,并使这些信息能够被访问。文件和非结构化内容也应是安全且高质量的。 确保文件和内容…...
【Erlang】【RabbitMQ】Linux(CentOS7)安装Erlang和RabbitMQ
一、系统环境 查版本对应,CentOS-7,选择Erlang 23.3.4,RabbitMQ 3.9.16 二、操作步骤 安装 Erlang repository curl -s https://packagecloud.io/install/repositories/rabbitmq/erlang/script.rpm.sh | sudo bash安装 Erlang package s…...
-导出表)
pe格式从入门到图形化显示(七)-导出表
文章目录 前言一、什么是Windows PE格式中的导出表?二、解析导出表并显示1.导出表的结构2.解析导出表3.显示导出表 前言 通过分析和解析Windows PE格式,并使用qt进行图形化显示 一、什么是Windows PE格式中的导出表? PE文件格式的导出表是P…...
)
图片地址生成二维码(通过前端实现)
文章目录 概要安装插件代码实例 概要 要将图片地址生成二维码,你可以使用 QrCode 库(假设你已经在项目中引入了该库)。以下是一个简单的示例代码,演示了如何使用 QrCode 库将图片地址转换为二维码并显示在页面上 安装插件 先下载…...

window安装maven和hadoop3.1.4
前面的文章已讲解如何安装idea和进行基本设置,本文主要带着大家安装配置好maven和hadoop. 大家不用去官网下载,直接使用我发给大家的压缩文件,注意解压后的文件夹不要放在中文目录下,课堂上我们讲解过原因。 这是我电脑上的路径&a…...
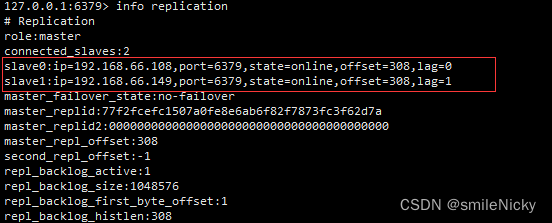
Redis系列之主从复制集群搭建
在上一篇博客,我们已经知道怎么搭建一个redis单机版,这篇博客基于之前的基础,来搭建一个redis主从同步,本博客框架是一主二从,一个主节点,其它两个从节点 实验环境 CentOS7Xshell6XFtp6Redis6.2.2 主从关…...

spring框架介绍
spring 1.优点 1)针对接口编程,解耦合 2)aop:变向切面编程,动态增加功能 3)方便集成框架,mybatis,hibernate,strust等 4)降低j2ee接口的使用难度 2.spring是干什么的 管理bean及bean…...

如果在 Ubuntu 系统中两个设备出现两个相同的端口号解决方案
问题描述: 自己的移动机器人在为激光雷达和IMU配置动态指定的端口时,发现激光雷达和深度相机配置的 idVendor 和 idProduct 相同,但是两个设备都具有不同的ttyUSB号,如下图所示 idVendor:代表着设备的生产商ID,由USB设…...

随手分享的APP链接,可能会让你“大型社死”
早晨上班路上,你在地铁百无聊赖地刷着短视频,看到一则好笑的,随手分享给了你的公司“饭搭子”,并配上了一串“哈哈哈哈哈哈”。 晚上下班路上你再次打开视频APP,发现首页弹窗给你推荐了一组“可能认识的人”ÿ…...

国内AI大模型已近80个,哪个最有前途?
根据中国新一代人工智能发展战略研究院发布的报告显示,目前全国已有3k+家人工智能企业,国内的AI大模型应该也近在200了!!! (原图图片过长了,这里就先放了20个) 面对如…...
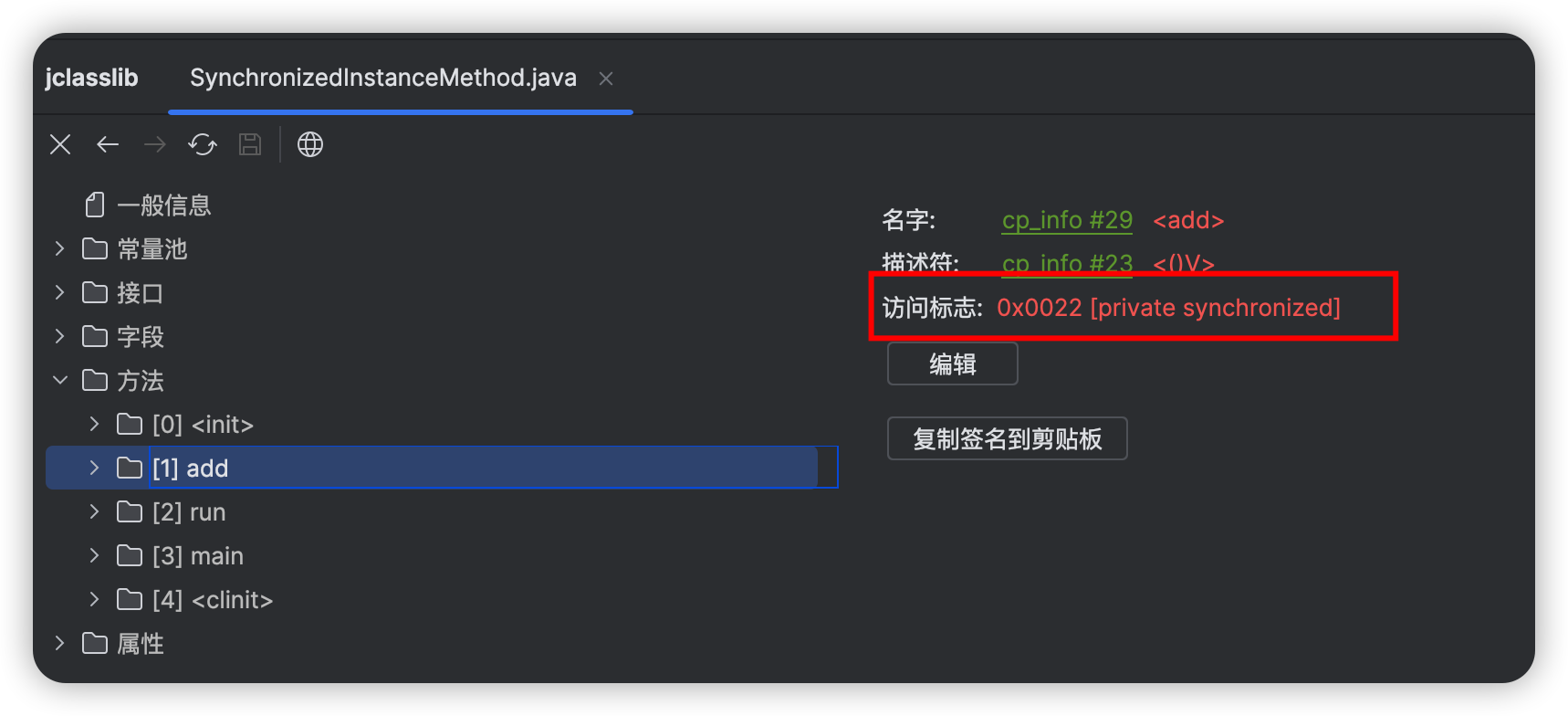
美团一面:说说synchronized的实现原理?问麻了。。。。
引言 在现代软件开发领域,多线程并发编程已经成为提高系统性能、提升用户体验的重要手段。然而,多线程环境下的数据同步与资源共享问题也随之而来,处理不当可能导致数据不一致、死锁等各种并发问题。为此,Java语言提供了一种内置…...
P1123 取数游戏(dfs算法)
题目描述 一个 NM 的由非负整数构成的数字矩阵,你需要在其中取出若干个数字,使得取出的任意两个数字不相邻(若一个数字在另外一个数字相邻 8个格子中的一个即认为这两个数字相邻),求取出数字和最大是多少。 输入格式 第…...

交叉验证(Cross-Validation)
交叉验证的基本概念 交叉验证通常用于评估机器学习模型在未知数据上的性能。它将数据集分成k个不同的子集,然后进行k次训练和验证。在每次迭代中,选择一个子集作为测试集,其余的子集作为训练集。这样,每个子集都用作过测试集&…...
keras使用介绍)
【kears】(01)keras使用介绍
文章目录 一.特点二.keras如何支持TensorFlow、CNTK 和 Theano2.1 使用 TensorFlow 后端引擎训练和评估模型2.2 使用 TensorFlow 后端引擎训练和评估模型2.3 使用 Theano后端引擎训练和评估模型2.4 不同深度学习框架如何选择1.1 keras.datasets:包含多种常用数据集1…...

2. TypeScript 安装与环境配置指南
TypeScript 是 JavaScript 的一个超集,它为 JavaScript 增加了类型系统和对 ES6 的支持。TypeScript 不仅能够帮助开发者捕获代码中的错误,还能提供更好的编辑器支持,包括代码补全、接口提示等。本文将详细介绍如何在您的开发环境中安装和配置…...

python pygame库的略学
文章目录 概述1. pygame的初始化和退出2. 创建游戏窗口(1)set_mode()(2)set_capyion()(3)update() 3. 游戏循坏与游戏时钟4. 图形和文本绘制(1)图形绘制(2)文…...

大模型日报2024-04-09
大模型日报 2024-04-09 大模型资讯 苹果预告超越ChatGPT的新AI模型ReaLM 摘要: 苹果公司最新宣布,即将推出一款名为ReaLM的人工智能模型。这款AI技术在理解复杂屏幕用户指令方面表现出高超的能力,并能与用户进行自然流畅的对话。ReaLM的推出预示着苹果在…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

【Linux】Linux安装并配置RabbitMQ
目录 1. 安装 Erlang 2. 安装 RabbitMQ 2.1.添加 RabbitMQ 仓库 2.2.安装 RabbitMQ 3.配置 3.1.启动和管理服务 4. 访问管理界面 5.安装问题 6.修改密码 7.修改端口 7.1.找到文件 7.2.修改文件 1. 安装 Erlang 由于 RabbitMQ 是用 Erlang 编写的,需要先安…...

C# winform教程(二)----checkbox
一、作用 提供一个用户选择或者不选的状态,这是一个可以多选的控件。 二、属性 其实功能大差不差,除了特殊的几个外,与button基本相同,所有说几个独有的 checkbox属性 名称内容含义appearance控件外观可以变成按钮形状checkali…...
