Containers--array类
Array 类
简介
Array 类是一个固定大小的数组,它的大小在编译时就已经确定了。Array 类的大小是固定的,因此它的大小不能改变。
数组是固定大小的序列容器:它们以严格的线性顺序保存特定数量的元素。
在内部,数组除了包含的元素之外不保留任何数据(甚至数组的大小也不保留,这是一个模板形参,在编译时固定)。
就存储大小而言,它与使用该语言的括号语法([])声明的普通数组一样有效。该类仅向其添加了一层成员函数和全局函数,因此数组可以用作标准容器。
容器属性
- Sequence(有序)
- 序列容器中的元素按照严格的线性顺序排列。各个元素通过它们在这个序列中的位置来访问。
- Contiguous storage(连续存储)
- 元素存储在连续的内存位置,允许常量时间随机访问元素。指向元素的指针可以偏移以访问其他元素。
- Fixed size aggregate(固定大小)
- 容器使用隐式构造函数和析构函数静态分配所需的空间。它的大小是编译时常数。没有内存或时间开销。
template < class T, size_t N >
- T: 容器中元素的类型
- size_t: 容器中元素的数量
成员函数

相关文章:

Containers--array类
Array 类 简介 Array 类是一个固定大小的数组,它的大小在编译时就已经确定了。Array 类的大小是固定的,因此它的大小不能改变。 数组是固定大小的序列容器:它们以严格的线性顺序保存特定数量的元素。 在内部,数组除了包含的元素之外不保留…...
LinqConnect兼容性并支持Visual Studio 2022版本
LinqConnect兼容性并支持Visual Studio 2022版本 现在支持Microsoft Visual Studio 2022版本17.5预览版。 添加了Microsoft.NET 7兼容性。 共享代码-共享相同的代码,以便在不同的平台上处理数据。LinqConnect是一种数据库连接解决方案,适用于不同的基于.…...
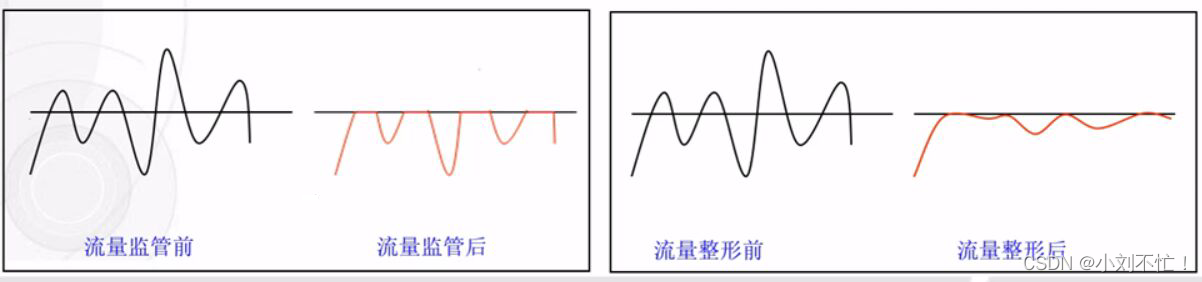
流量监管与整形
流量监管与整形概览流量监管介绍流量监管令牌桶流量监管的具体实现单桶单速流量监管双桶单速流量监管双桶双速流量监管流量整形介绍GTS(Generic Traffic Shaping)LR(Line Rate)流量整形与流量监管的区别概览 流量整形是对报文的速…...

详解init 容器
什么是init容器 init 容器是一种特殊容器,在 Pod 内的应用容器启动之前运行。Init 容器可以包括一些应用镜像中不存在的实用工具和安装脚本。 你可以在 Pod 的规约中与用来描述应用容器的 containers 数组平行的位置指定 Init 容器 每个 Pod 中可以包含多个容器&…...

RequestResponseBodyMethodProcessor
既是一个参数解析器,也是一个返回结果处理器。 1.持有消息转换器的集合 protected final List<HttpMessageConverter<?>> messageConverters;2.作为参数解析器,例如对RequestBody标识的参数进行解析 判断是否支持当前类型的参数 Overrid…...
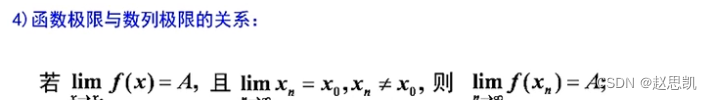
函数的极限
目录 函数的极限 函数极限的定义: 例题: 左右极限: 自变量趋于无穷大时函数的极限: 例题: 函数极限的性质: 函数极限与数列极限之间的关系: 函数的极限 函数极限的定义: 一句…...

dnf命令使用
1. 简介 DNF是新一代的rpm软件包管理器。他首先出现在 Fedora 18 这个发行版中。而最近,它取代了yum,正式成为 Fedora 22 的包管理器 DNF包管理器克服了YUM包管理器的一些瓶颈,提升了包括用户体验,内存占用,依赖分析…...
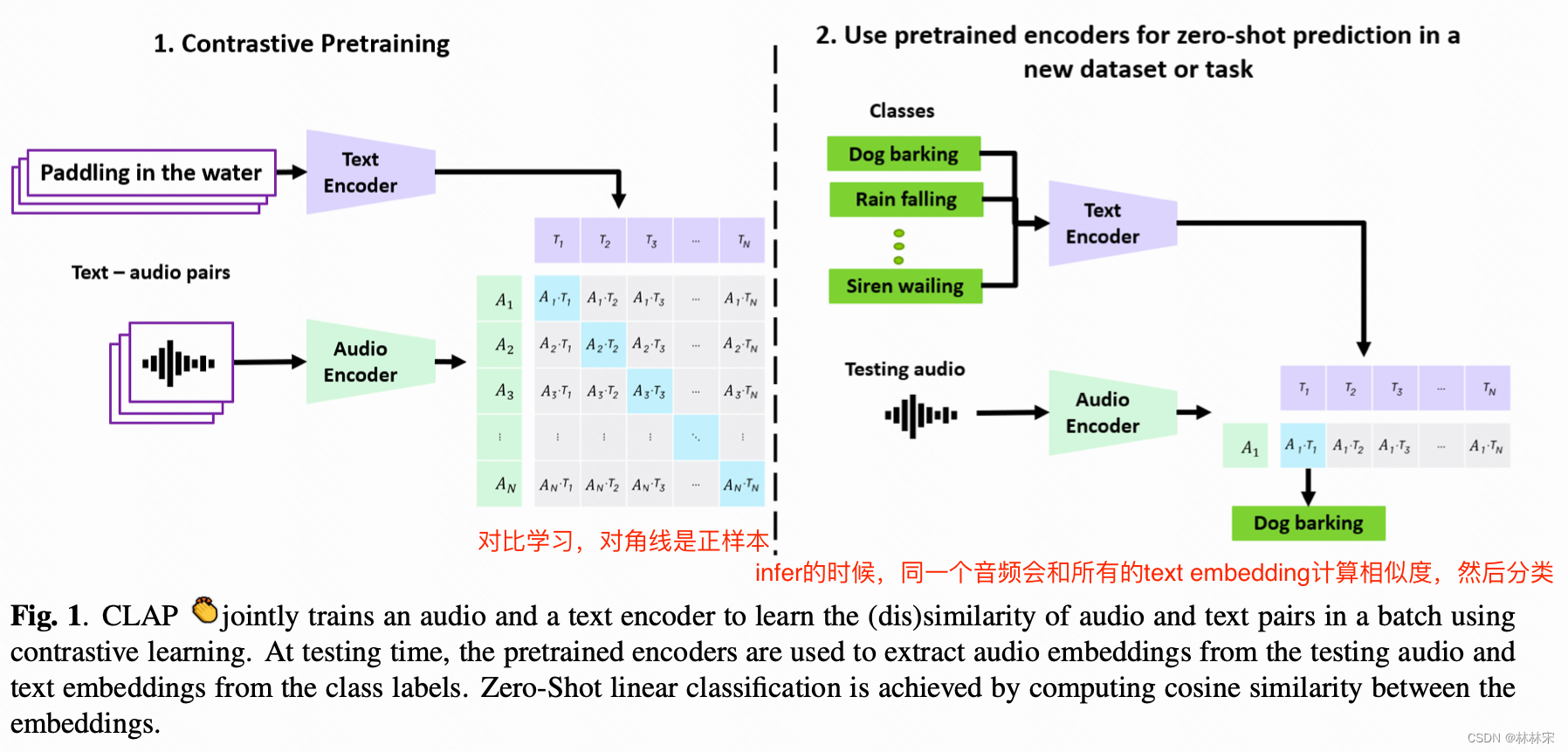
CLIP CLAP
文章目录CLIPabstractintroCLAP: LEARNING AUDIO CONCEPTS FROM NATURAL LANGUAGE SUPERVISIONabstractmethodCLIP open AI2021.2代码&预训练模型 abstract 原有的基于有监督数据训练的计算机分类任务,在面对新的分类目标时泛化性和可用性都会变差࿱…...

Debezium报错处理系列之五十二:解决Sql Server数据库安装后修改主机名导致sqlserver数据库实例名称没有修改从而无法设置CDC的问题
Debezium报错处理系列之五十二:解决Sql Server数据库安装后修改主机名导致sqlserver数据库实例名称没有修改从而无法设置CDC的问题 一、完整报错二、错误原因三、解决方法Debezium报错处理系列一:The db history topic is missing. Debezium报错处理系列二:Make sure that t…...

scratch老鹰捉小鸡 电子学会图形化编程scratch等级考试二级真题和答案解析2022年12月
目录 scratch老鹰捉小鸡 一、题目要求 1、准备工作 2、功能实现 二、案例分析 <...
)
概率论小课堂:公理化过程(大数据方法解决问题的理论基础)
文章目录 引言I 初等概率论1.1 19世纪概率论的最大难题1.2 伯努利版本的大数定理1.3 切比雪夫版本的大数定理II 现代概率论(用公理来描述概率论)2.1 柯尔莫哥洛夫2.1 用公理来描述概率论III 最基本的概率论定理3.1 互补事件的概率之和等于13.2 不可能事件的概率为零引言 前苏…...

WOW64 IsWow64Process GetNativeSystemInfoWindows System32 SysWOW64
最近开发有遇到这方面的一些知识点,在此记录下。首先,什么是WOW64?在知道这个之前我觉得需要了解一下,C:\\Windows\\System32和C:\\Winodws\\SysWOW64这两个文件夹的区别,Windows系统最开始的时候出的就是32bit的系统&…...

Spring Boot 3.0系列【10】核心特性篇之应用配置的高阶用法
有道无术,术尚可求,有术无道,止于术。 本系列Spring Boot版本3.0.3 源码地址:https://gitee.com/pearl-organization/study-spring-boot3 文章目录 前言1. 命令行2. JSON3. 外部化配置3.1 配置文件加载位置3.2 导入配置3.2 属性占位符4. 加密配置5. 加载YML配置文件6. 配…...

Java int类型数值比较总结
如果是int类型,判断相等的话直接使用 ""来判断,例如: int i 10; int j 10; System.out.print(i j); 如果是Integer类型,则可以使用equals方法进行相等比较。 int与Integer的基本使用对比 (…...
Pyspark基础入门5_RDD的持久化方法
Pyspark 注:大家觉得博客好的话,别忘了点赞收藏呀,本人每周都会更新关于人工智能和大数据相关的内容,内容多为原创,Python Java Scala SQL 代码,CV NLP 推荐系统等,Spark Flink Kafka Hbase Hi…...

汽车娱乐系统解决方案
Danlaw在汽车和航空航天行业里是全球知名的技术和服务供应商,致力于提供更加安全与智能的系统。Danlaw以突破性技术和高效开发、动态环境的自适应解决方案而闻名。Danlaw优秀的联网汽车解决方案使之成为全球大型互联设备供应商之一。 一 信息娱乐系统测试 | 风丘科…...

Go语言结构体,这一篇就够了
Go语言结构体,这一篇就够了1.结构体的概念2.结构体的定义3.结构体的实例化4.结构体初始化5.构造函数6.方法和接收者方法接收者7.嵌套结构体8.结构体的“继承”9.结构体与JSON序列化10.结构体标签(Tag)Go语言中没有“类”的概念,也…...

【python】各种排序算法代码大集合
超级好用的口诀: 时间复杂度:快些以nlogn的速度归队。 稳定性:心情不稳定,快些选一堆好友来聊天吧。 直接插容易插变O(N),起泡起得好变O(N).(初始序列已经有序) 插入排序法在近乎有序的情况下,效率特别高,通过插入排序,可以引申出希尔排序 归并排序:左半部分排好序…...
K8S Pod健康检查
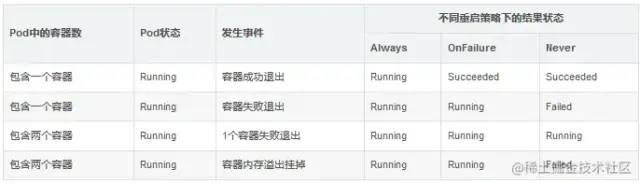
因为 k8s 中采用大量的异步机制、以及多种对象关系设计上的解耦,当应用实例数 增加/删除、或者应用版本发生变化触发滚动升级时,系统并不能保证应用相关的 service、ingress 配置总是及时能完成刷新。在一些情况下,往往只是新的 Pod 完成自身…...
NFS服务器与CGI程序详解
目录 NFS 服务器 一,NFS 服务器简介 二,NFS的使用 三,客户端使用 autofs 自动挂载 1,autofs产生的原因 四,autofs的安装与配置文件 五,autofs的使用 www服务器---cgi程序 CGI程序的应用 NFS 服务器 一&a…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...
